基于Beta族的相關貝葉斯模型在準備金中的應用

劉 燕，李云瑞

（1.鄭州大學 數學與統計學院；2.河南省金融工程重點實驗室，鄭州 450001）

0 引言

未決賠款準備金是保險公司為將來未決賠款的賠付提前計提的準備資金，計提充足的未決賠款準備金是維護投保人權益和保障保險公司正常的償付能力的重要工作。在我國,非壽險保險公司準備金的提取大多使用傳統的估算方法，比如鏈梯法，案均賠款法，B-F方法等。這些統計類方法使用比較簡單，但沒有重視隨機因素的影響，準確度并不很高。

由于各種保險特征因素的影響，如索賠頻率、索賠額度及理賠方式，都會使各進展年索賠額之間具有一定的相關性，因此就會導致使用獨立假設下的貝葉斯模型來估計未決賠款準備金時，與實際準備金的支出額有較大偏離。因此，需要考慮增量賠款的相關性對未決賠款準備金評估模型的影響。Gilks等（1995）[1]在模型中通過一個潛在過程來構造相關Gamma過程，并應用此相關Gamma過程來體現事故年之間的相關性。由于Beta族分布類是比Gamma分布更廣的分布類型，Gamma分布僅僅是Beta族分布類的一個特例，所以本文將Gamma過程推廣到Beta族分布類來建立未決賠款準備金評估模型。下面給出基于Beta分布類的相關過程的理論模型，并對其中的相關參數使用貝葉斯估計。本文假設事故年i和進展年j的增量賠款額為Xij，即第i個事故年發生的索賠在第j個進展年的所有賠款。但對于不同的流量三角形中不同的事故年i和i′(i≠i′)，未決增量賠款過程和是相互獨立的。

1 基于Beta族的相關貝葉斯模型

一般假設Beta分布族的分布密度函數為：

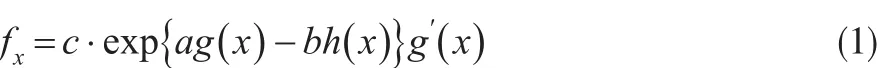
這里a、b、c為常數，h(x)、g(x)均為x的可導函數，且滿足性質h′(x)g′(x)=x。

假設增量賠款Xij服從Beta族分布，即對所有的i有，Xi1密度函數為：

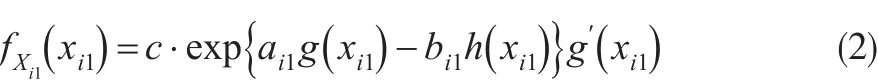
Zij|Xi，j-1的密度函數為：

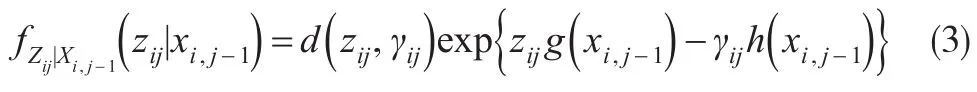
并且有：

由以上的構造過程可以發現，保單組合的第i個事故年的增量賠款額Xi，j-1和Xij通過潛在的過程Zij建立了相關性，并且可以證明其具有下面的性質：

定理1：保單組合的第i個事故年的增量賠款額Xij為Beta族分布，且過程是Markov過程，則有如下性質：

(1)由分部積分法得：

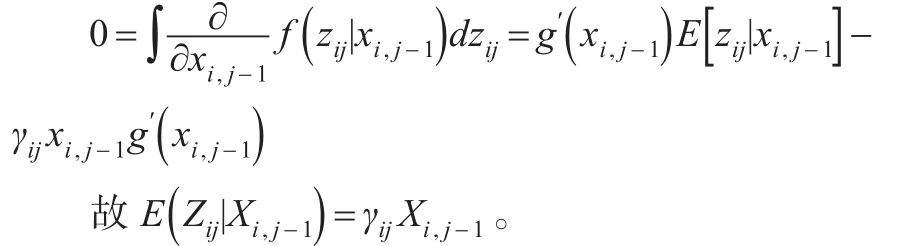
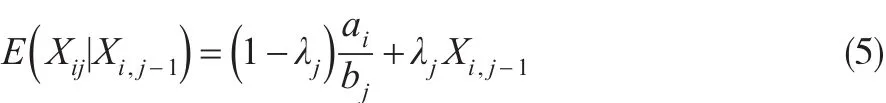
其中，ai為賠款的平均總額，bj為增量賠款占賠款平均總額的百分比：

由式(6)可知λj∈( )0， 1 ,j=1， 2， … ，n，從式(5)可以得到，Xi，j在Xi，j-1條件下的期望是第 i個事故年的增量賠款額Xi，j的期望值和前一進展年的增量賠款額Xi，j-1的以λj為權重的加權平均。其中λj越大Xi，j和Xi，j-1的相關程度越強。若有γj=0 ，則Xi，j和Xi，j-1的相關程度為0，此時相關貝葉斯模型就退化為獨立的貝葉斯模型。

2 相關貝葉斯模型的參數估計

使用相關貝葉斯模型計算未決賠款準備金時，首先需要根據貝葉斯方法[2]估計其中的參數，ai、bj和λj。令：

首先，假設各參數的先驗分布為：

其次，在上面的假設下，可以得到變量X，Z的聯合分布。

定理2：假設未決增量賠款Xi，j服從Beta族分布，其流量三角形中上三角的所有變量X，Z的聯合分布滿足：

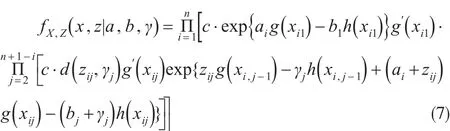
最后，應用貝葉斯原理，可以得到未決賠款分布中各參數的后驗分布如下定理3所述：

定理3：未決賠款額增量賠款分布中參數滿足下列性質：

(1)參數ai的條件后驗分布：對于所有的i=1， …，n有：

(2)參數bj的條件后驗分布：

①當j=1時有，

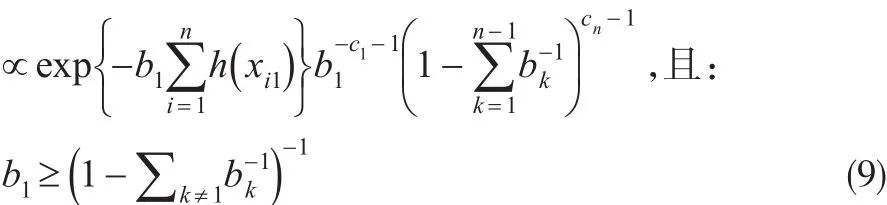
②當j=2， …，n-1時有：

③當j=n時有：

(3)參數γj的條件后驗分布：對于所有的j=2，…，n-1有：

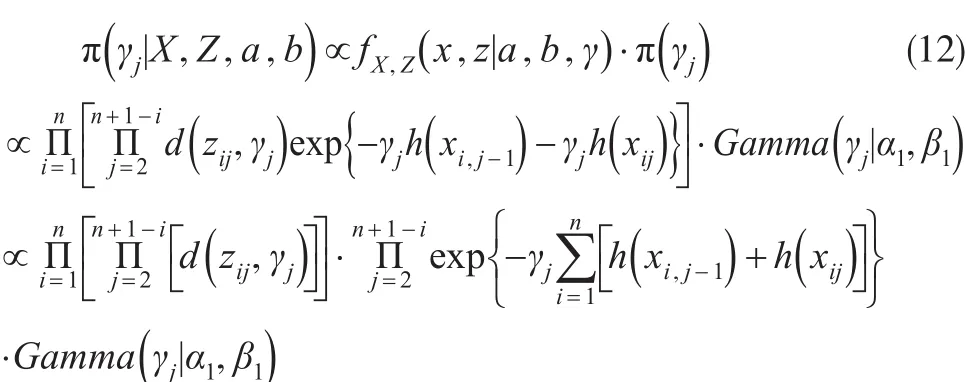
模型中參數后驗均值的計算比較復雜，可以應用數學軟件分析其數值解，再抽樣得到后驗分布的樣本，在此基礎上分析參數的后驗均值。

3 未決賠款準備金的預測

在流量三角形中估計未決賠款準備金，需要預測未決增量賠款流量三角形中未來未決賠款的增量的大小，本文假設上三角已知的增量賠款Xij（i=1， …，n,j=1， …，n-i+1）和需要預測估計的下三角中的未決增量賠款有相同的分布形式，根據Zij在條件X下的分布：

可以進一步得到增量賠款的概率密度函數：

若對所有的i=1， …，n，有，則在條件下的預測分布有如下形式：

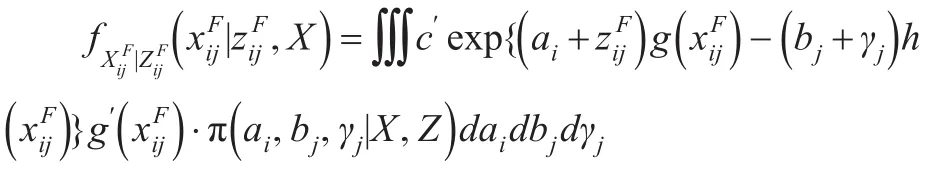
4 預測模型的評價

由于在相關貝葉斯模型中不適合使用方差，均方誤差等指標來評價模型的優劣。Ibrahim和Laud[4]于1994年提出L測度，測度值L()x是方差和偏差的組合，他的大小可以體現模型預測的誤差，具體形式如下：

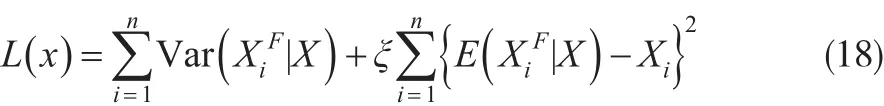
5 實證研究

模型中考慮的流量三角形均為增量賠款流量三角形，使用Taylor和Ashe所給的未決增量賠款數據集，本文假設未決增量賠款隨機變量Xij服從伽馬分布，為了對比模型預測未決賠款準備金的情況，可以分別應用獨立Gamma過程和相關Gamma過程來預測未決賠款準備金，分別將兩個模型的估計結果進行比較和分析（見表1）。這里應用R軟件[5]實現預測模型，并通過Gibbs抽樣[6]的方法來估計其中的參數。

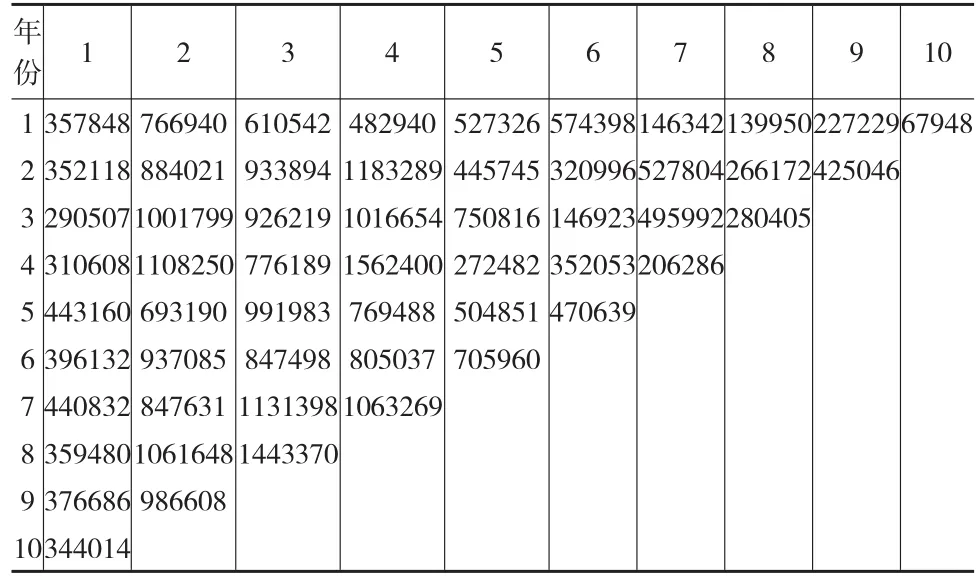
表1 增量賠款流量三角形

首先應用獨立貝葉斯模型[7]來預測未決賠款準備金，即Xij是相互獨立的。

a=(4.168， 5.925， 5.5013， 5.0212， 5.7365， 5.9001，6.4997， 7.2953， 6.2659， 5.4173)，（以百萬為單位），

1b=(0.04， 0.15， 0.18， 0.17， 0.10， 0.08， 0.07， 0.05，0.08， 0.03)

由以上估計的模型參數的后驗均值，可以估計增量賠款流量三角形下三角的數據和各事故年的未決賠款準備金，通過R語言編程實現模型，可以得到結果如下頁表2所示。

表2給出了所有事故年在各個進展年的增量賠款額和各事故年的未決賠款準備金，再對各事故年的準備金求和，即保險公司所需計提的未決賠款準備金約為2132萬元。

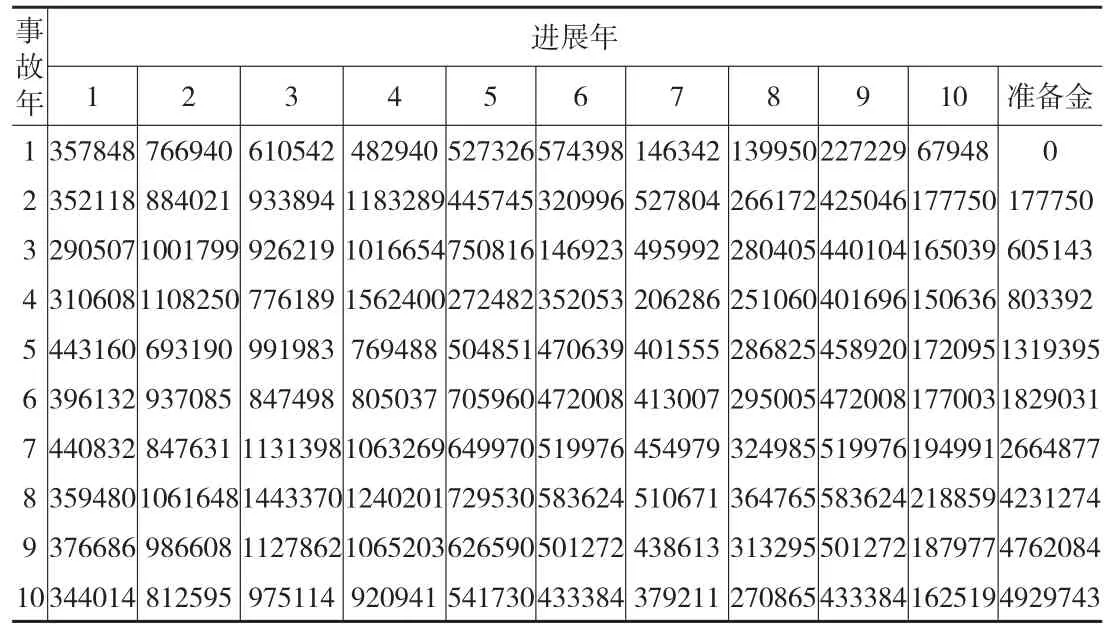
表2 獨立貝葉斯模型增量賠款和準備金估計值

然后應用相關貝葉斯模型來預測未決賠款準備金，即Xij是相關的。

對所有的i有：

這里需要估計的參數有αi，βj，γj，給定參數的先驗分布為：

αi～Gamma( )0.001， 0.001，β～I-Dir(1， …，1)，γj～Gamma( )0.01， 0.01

α=(5.1714， 7.4139， 6.3995， 5.4037， 7.4706，7.8652，8.4857， 9.0457， 7.9534， 6.6329)（百萬）

1β=(0.06， 0.28， 0.15， 0.16， 0.07， 0.06， 0.05， 0.04，0.06， 0.02)

λ=(0.70， 0.65， 0.66， 0.13， 0.03， 0.02， 0.02，0.01， 0.01)

由以上估計的各參數的后驗均值，可以估計增量賠款流量三角形下三角的數據和各事故年的未決賠款準備金，通過R語言編程實現，得到未決賠款準備金如表3所示。

表3給出了所有事故年在各個進展年的增量賠款額和各事故年的未決賠款準備金，再對各事故年的準備金求和可得總的未決賠款準備金為2061萬元。

分別對ξ=0， 1 2， 1三個不同的取值分別計算兩種模型估計未決賠款準備金的L測度值：由表4可知，相關貝葉斯模型的L測度在各種ξ取值下估計的誤差值都比獨立貝葉斯模型的L測度值要小。顯然，針對這個實例估計的未決賠款準備金，使用相關貝葉斯模型估計的值更準確合理。

6 結束語

本文將Enrique de Alba和Luis E.Nieto-Barajas(2008)提出的相關貝葉斯模型中增量賠款的分布推廣到Beta分布族，建立基于Beta族分布的未決賠款準備金評估模型。在此理論基礎上，使用流量三角形來預測保險公司所需計提的未決賠款準備金。并使用R軟件編程實現準備金的隨機評估模型，通過Gibbs抽樣估計模型中的參數ai、bj和λj，計算未決賠款準備金的估計值和估計偏差的L測度值，分析估計值的性質和優劣。但文中沒有考慮各事故年增量賠款之間的相關性，而且抽樣統計分析也還存在一定的誤差，這些問題都還有待于進一步的研究。

表3 相關貝葉斯模型增量賠款和準備金估計值

表4 兩種模型的L測度值比較