基于經驗模態分解的軌道不平順時頻特征分析

楊友濤,　劉國祥

(1. 西南交通大學地球科學與環境工程學院, 四川 成都 611756; 2. 西南交通大學高速鐵路運營安全空間信息技術國家地方聯合工程實驗室, 四川 成都 611756; 3. 西南交通大學土木工程學院, 四川 成都 610031)

軌道不平順是指軌道的實際位置、幾何尺寸相對設計位置和設計尺寸的偏差,是由很多隨機因素共同作用的結果.主要包括線路施工過程中的偏差、鋼軌的初始平直性、道床、路基等構筑物的不均勻沉降及殘余變形積累,以及機車車輛等荷載的不規則變化的動力作用[1]等因素.由于這些不確定性因素的共同作用,使得軌道不平順具有隨機性,主要采用均值、方差等統計數據表示其特性.目前,我國軌道幾何狀態評價主要采用局部幅值超限方法和軌道質量指數方法,這兩種方法從空間域(線路里程)幅值方面進行評價,具有一定的局限性.

有學者利用信號的時頻分析方法對軌道動態不平順數據進行分析,文獻[2-3]中利用小波分析理論對軌道不平順局部高頻災害進行檢測，提取不同波長范圍的軌道不平順.文獻[4-5]中利用小波和Wigner-Ville相結合的方法對軌道不平順特征進行提取與分析.文獻[6]中利用短時傅里葉變換、魏格納變換和Gabor變換等時頻分析方法分析了軌道實測振動加速度信號,提取了長波不平順信號.短時傅立葉變換采用固定時間窗口的函數進行計算,不能根據信號的特點來調整時間分辨率和頻率分辨率,沒有自適應能力.小波變換克服了短時傅立葉變換時間窗口大小不隨頻率變化的缺點,可根據信號頻率的高低自適應調整時頻窗口的大小,但仍受Heisenberg不確定原理限制,不能精確表示頻率隨時間的變化.另外,各個小波基函數的適用范圍不一樣,選擇適合待分析信號的小波基函數是小波分析的難點,使小波分析不具有自適應性.

與以上建立在先驗基函數上的時頻分析方法不同,經驗模態分解(empirical mode decomposition, EMD)是以信號本身的時間尺度特征為基礎的自適應分解方法,更適合非線性、非平穩信號分析.經驗模態分解與希爾伯特變換相結合,更能揭示隱藏于信號中的內在物理信息[7].針對經驗模態分解僅能處理一元數據的不足, Rehman提出適合于多通道信號分析的多元經驗模態分解(multivariate empirical mode decomposition, MEMD)[8].多元經驗模態分解把多元數據分解為具有相同數目的本征模態函數,可以減少各層模態混疊和尺度不對齊的問題,具有自適應性[9].本文利用多元經驗模態分解(intrinsic mode functions, IMF)和希爾伯特變換方法,對軌道幾何不平順的時頻特征分布進行分析,為線路養護維修、列車安全運行提供技術支持.

1　希爾伯特-黃變換方法

1.1　多元經驗模態分解

經驗模態分解是以數據驅動方式把非線性、非平穩信號分解為多個幅值-頻率調制的本征模態函數以及殘余分量[7],其表達式為

(1)

式中:x(t)為信號;cm(t)為IMF;m為IMF層數;r(t)為剩余分量;t為時間.

本征模態函數包含不同的頻率成份,反映了信號的不同波動情況.每個本征模態函數必須滿足條件[7]:(1) 在整個數據范圍內,極值點和過0點的個數相等或相差1個;(2) 由極大值和極小值計算的包絡值之和為0.

經驗模態分解通過循環篩分的方法把滿足上述兩個條件的IMF分解出來.在一元經驗模態分解中,通過對信號的極大值和極小值分別內插計算獲取上、下包絡線,然后對其取平均得到局部均值[7],對于多元數據,不能直接定義極值.

為解決這個問題,多元經驗模態分解把多元信號X(t)=(x1(t),x2(t),…,xn(t))沿不同方向投影到n維空間上,計算這些投影序列的極值并進行內插,得到投影序列的包絡線,這些包絡線的平均值即為多元信號的局部均值[8].多元經驗模態分解的計算過程如下:

(1) 在n-1維超球面上選擇合適的均勻采樣點集θk,獲得n維空間的方向向量集vθk,k為方向向量個數,k=1,…K;

(2) 計算多元信號X(t)在每個方向向量vθk上的投影向量Pθk(t);

(3) 找出所有投影向量集中,每個投影向量極大值所對應的時刻ti,θk,i為極大值點的序號;

(4) 利用樣條函數對極值點(ti,θk,X(ti,θk))進行插值,獲得K條包絡曲線eθk(t);

(5) 計算K個方向向量的包絡線均值

(2)

(6) 提取高頻細節信號d(t),d(t)=X(t)-m(t).如果d(t)滿足多元IMF的停止準則,記C1(t)=d(t)為第 1層多元IMF,將X(t)-d(t)作為(2)中輸入信號,繼續提取多元IMF;否則,將d(t)作為輸入信號繼續迭代計算.

經過多元經驗模態分解后,多元信號分解為不同尺度的多元IMF和多元剩余分量之和的形式為

(3)

式中Cm(t)=(c1，m(t),c2，m(t),…,cn，m(t))為n元IMF;R(t)=(r1(t),r2(t),…,rn(t))為n元剩余分量.

1.2　希爾伯特譜分析

通常,瞬時頻率和瞬時幅值用于表征非平穩、非線性信號的短暫特性.但是,對于多分量組成的非平穩信號,瞬時頻率沒有明顯的物理意義.所以,首先利用經驗模態分解將多分量信號分解為一系列單分量的IMF,然后利用希爾伯特變換計算其瞬時頻率和瞬時幅值.對于單一成分的本征模態函數cj,m(t),其希爾伯特變換為

(4)

式中:P為柯西主值；j為多元變量序號.

相應的解析信號形式為

Zj，m(t)=cj,m(t)+iH(cj,m(t))=aj,m(t)eiφj,m(t).

(5)

信號瞬時幅值aj,m(t)和瞬時相位φj,m(t)的計算式為

(6)

通過對瞬時相位求導,可得瞬時頻率為

(7)

通過希爾伯特變換計算瞬時頻率,有時會出現較大的波動,甚至出現負頻率的情況.同時,希爾伯特變換具有端點效應,即在信號兩端的瞬時頻率具有能量泄漏的問題[10].文獻[10]中在希爾伯特變換求取瞬時頻率的基礎上,提出標準化希爾伯特變換,采用經驗調頻-調幅分解方法,減弱了IMF中的調幅分量,僅保留了調頻分量,從而使瞬時頻率的計算不再受Bedrosian等式的限制.文中軌道不平順的瞬時頻率采用標準化希爾伯特變換計算.

通過對每一個IMF進行希爾伯特變換,信號xj(t)表示為

(8).

用式(8)可在三維坐標圖中,將瞬時幅值和瞬時頻率表示為時間的函數,即在時間和頻率聯合平面內表示幅值的變化.這種幅值隨時間和頻率(f)變化的分布函數為信號的希爾伯特譜,其表達式為

(9)

2　軌道幾何不平順數據分析

軌道幾何不平順用軌距、水平、左高低、右高低、左軌向、右軌向和扭曲7個參數來描述,其表示為隨里程變化的隨機函數.

本文選取軌道檢查車在滬寧城際上的軌道動態檢查數據進行分析,檢測速度為252 km/h,樣本數據里程為上行K104+000.00～K104+999.75,軌檢車數據采樣間隔為0.25 m.

2.1　軌道不平順多尺度分解

對預處理后的軌道不平順信號進行多元經驗模態分解,得到13層IMF(C1～C13)和1個趨勢項,分解結果見圖1、2.

由圖1、2可以看出,隨著IMF序號的增加,其空間變化尺度逐漸增大;7個軌道不平順參數中,相同序號的IMF具有相近的空間變化尺度.根據多元經驗模態分解這一特點,按信號內在規律分解出多元序列相近尺度的分量.軌距和右軌向不平順的第2層和第3層IMF在里程K104+485.00前后有大的幅值異常值,見圖示.在數據預處理階段采用3倍中誤差準則并沒有探測出該里程位置的異常值,但是經過經驗模態分解后有異常值出現.

2.2　軌道不平順頻率分析

對軌道不平順分解的各層IMF進行標準化希爾伯特變換,計算各個IMF的瞬時頻率和瞬時幅值.

為直觀表示軌道不平順各IMF瞬時頻率的變化,計算其平均頻率.計算平均頻率有兩種方法:

(1) 根據極值點或過0點個數計算平均頻率[11-12];

(2) 利用信號的瞬時頻率計算平均頻率[13-14].

按極值點和過0點個數確定平均頻率的方法,在高階IMF中,由于極值點和過0點位置的不均勻性,平均頻率的計算結果誤差較大.

文獻[14]中利用瞬時頻率的算術平均值和能量加權均值表示平均頻率,能量權重平均頻率可寫為

(10)

式中:L為時間長度.

根據瞬時頻率所占的權比來計算平均頻率的幾種方法,更能直觀的反映每層IMF的頻率變化情況[13-14].本文采用瞬時頻率能量權重的方法,即按式(10)計算軌道不平順各IMF的平均頻率及平均頻率標準差.與式(10)相對應,平均頻率標準差也考慮能量權重,則加權標準差計算式為

(11)

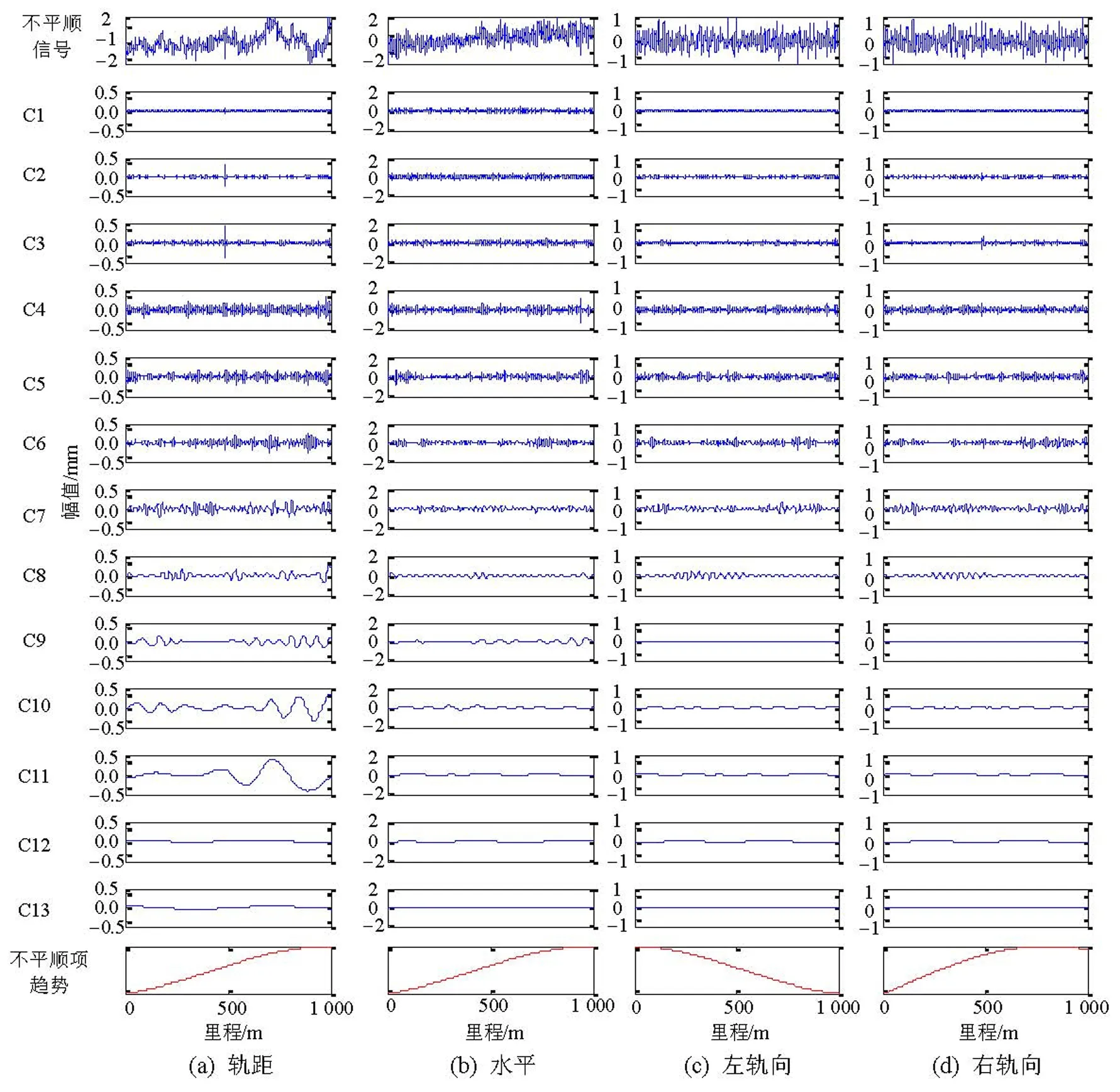
圖1　軌道幾何不平順多元經驗模態分解結果 (A)Fig.1　MEMD results of irregularities in track geometry (A)

圖2　軌道幾何不平順多元經驗模態分解結果(B)Fig.2　MEMD results of irregularities in track geometry (B)

為減少希爾伯特變換邊界效應對平均頻率的影響,在軌道不平順的每個IMF平均頻率及標準差計算中剔除了樣本數據兩端的部分數據,其計算結果如表1所示.表中,相對標準差指每個IMF的平均頻率的標準差與其平均頻率的比值.

從表1可以看出:(1) 軌道不平順7個參數中,經多元經驗模態分解得出的同層IMF的平均頻率基本一致,每層IMF中平均頻率相對較差最大的為第13層的IMF,其原因是高階IMF的平均頻率計算誤差較大造成的;其他各層的平均頻率相對較差很小,說明經多元經驗模態分解的軌道不平順各層的IMF頻率具有一致性[9].(2) 每個軌道不平順參數的各層IMF的平均頻率逐漸減少,并且其值約為上一層IMF平均頻率的1/2.文獻[9]中通過對白色噪聲進行經驗模態分解,得出該方法具有二進濾波特性,軌道不平順數據的頻率分布與白色噪聲具有相似性,說明軌道不平順數據具有隨機特性.(3) 不同序列的同層IMF的平均頻率相對標準差差別較小,其中：第1層IMF的相對標準差較大,其值為0.4左右,說明第1層瞬時頻率波動較大,可能是信號中含有高頻噪聲所致;第2～13層IMF的相對標準差均較小,說明多元經驗模態分解方法獲得的軌道不平順的頻率帶寬較窄,瞬時頻率波動較小.

表1　軌道不平順各層IMF的平均頻率和相對標準差Tab.1　Average frequency and relative standard deviation of IMFs of track irregularity

多元經驗模態分解方法是根據數據本身的波動情況自適應的分解為多層IMF.本文選取的軌道不平順樣本數據被分解為13層,其平均波長(空間頻率的倒數)范圍為0.7～761.4 m,說明軌道不平順數據是由不同波長組成的多分量隨機函數.

目前軌道檢查車的最大檢測波長為200 m,由多元經驗模態分解方法得出的最大波長遠超此范圍,說明利用多元經驗模態分解方法獲得的IMF有虛假波長成份,所以如何根據軌道不平順數據的實際波動情況選擇有效的IMF也是需要解決的問題.

2.3　軌道不平順能量分布

文獻[14]中在分析小波尺度圖的基礎上,提出多元經驗模態分解尺度圖,即用各層IMF的瞬時幅值的平方來表示信號不同尺度的能量變化.根據式(8),信號的多元經驗模態分解尺度圖可表示為

(12)

多元經驗模態分解尺度圖在時間和尺度的聯合平面內表示能量的變化情況,軌道不平順7個參數的多元經驗模態分解尺度圖如圖3所示.

由圖3可以看出,軌距和水平不平順的能量分布較為廣泛,涵蓋在第3～11層IMF范圍內,軌距的第11層IMF能量所占比重較大,其能量主要分布在低頻部分;軌向和高低4個不平順參數的能量主要集中在中間頻段的IMF中,低頻和高頻段范圍的能量幾乎可以忽略不計;扭曲不平順的能量主要分布在前6個IMF中,即高頻部分.

綜上所述，通過多元經驗模態分解尺度圖也能確定軌道不平順在不同尺度內沿里程方向上能量的突變,可為精確查找軌道病害,進行養護維修提供了基礎.

表2為根據多元經驗模態分解尺度圖統計出的各層IMF能量所占的比例.由表2可以看出：

(1) 軌距不平順中，第11層IMF所占能量達到40.9%,主要原因是在里程K104+500.00～K104+980.00范圍內軌距不平順幅值有大的波動.

(2) 軌向和高低能量分布比較集中,第4～8層 的IMF能量之和比例達到90%以上,從表1可知，第4～8層的IMF對應的空間平均波長為4.37、7.58、14.11、23.96、35.56 m,即能量主要分布在波長為4～36 m的范圍;同時在每層IMF中左右軌向、左右高低的能量百分比比較一致,說明左右軌道的軌向、高低的能量分布具有相關性.

(3) 扭曲不平順能量主要集中在高頻部分,其中第4、5層IMF能量所占比例均大于30%；第8～13層IMF所占能量比例之和僅為1.5%,低頻段能量的影響很小.

多元經驗模態分解尺度圖能清晰的標識軌道不平順在不同尺度上的能量分布.軌道不平順樣本數據中,除軌距不平順外,其他不平順的能量主要分布在中波區段,且能量分布相對集中.通過以上分析,能更好的掌握軌道不平順的能量和波長分布規律,可以有針對性的對軌道進行養護維修,提高鐵路運行的安全性.

圖3　軌道不平順多元經驗模態分解尺度圖Fig.3　MEMD-based scalograms of track irregularity

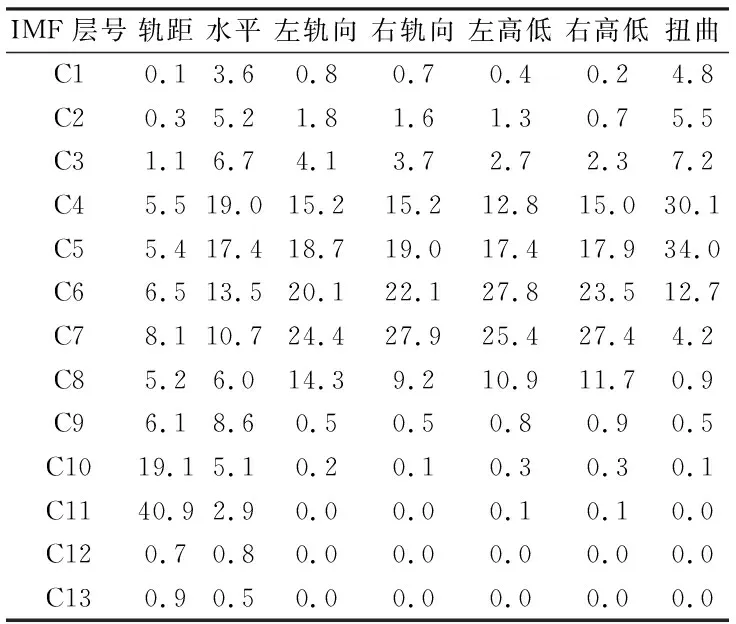
IMF層號軌距水平左軌向右軌向左高低右高低扭曲C10.1 3.60.80.70.40.24.8C20.35.21.81.61.30.75.5C31.16.74.13.72.72.37.2C45.519.015.215.212.815.030.1C55.417.418.719.017.417.934.0C66.513.520.122.127.823.512.7C78.110.724.427.925.427.44.2C85.26.014.39.210.911.70.9C96.18.60.50.50.80.90.5C1019.15.10.20.10.30.30.1C1140.92.90.00.00.10.10.0C120.70.80.00.00.00.00.0C130.90.50.00.00.00.00.0

3　結　論

基于多元經驗模態分解方法和希爾伯特變換,對高速鐵路軌道動態不平順進行時頻特征分析和應用研究,得出以下主要結論:

(1) 多元經驗模態分解方法用于分析多元數據序列,減少了標準經驗模態分解方法中的模態混疊和多元序列尺度不對齊的問題,具有很好的自適應性和時頻局部化能力.希爾伯特變換計算多元序列的瞬時頻率和瞬時幅值,能反映多元數據序列的局部時頻分布特征.

(2) 用多元經驗模態分解方法,分解出的軌道幾何不平順各層IMF的頻率帶寬較窄,軌道不平順在不同尺度下的頻率波動較小;軌道不平順不同參數的同層IMF的平均頻率相差較少,具有一致性.

(3) 多元經驗模態分解尺度圖能直觀的反映軌道不平順的能量分布,樣本數據的軌距不平順能量主要分布于中長波區段,波長頻段范圍較廣;軌向和高低能量分布相對集中,主要集中于空間波長4～36 m范圍;扭曲的能量主要集中分布在波長為4.9、7.6 m的兩個尺度內.

為更好的提取軌道不平順的時頻特征,應對整條線路軌道不平順數據按線路類型、軌道結構以及線下結構等分門別類的進行特征分析,同時比較軌道不平順數據在不同檢測時間的時頻變化特征.