一種基于網絡協作度的作戰效果評估方法

劉經天，田建宇，孫雅薇，劉衛新

（北方自動控制技術研究所，太原 030006）

0 引言

作戰效果評估是指為實現軍事目的或達成預定的軍事狀態，作戰指揮人員通過不斷評估作戰環境與作戰進程，并將之與預期設想與戰略意圖相比較，從而對作戰結果進行評價與估量。準確有效的作戰效果評估對指揮人員感知戰場態勢、改進作戰計劃有著重大意義。目前對作戰效果的評估方法主要有3種：文獻［1］提出了組織效能模型，通過研究作戰組織行為來評價作戰效能；文獻［2］通過建立模擬系統，研究采用不同的裝備所產生的作戰效果；文獻［3］提出基于認知的效果分析方法，通過系統集成的認知工程方法評估作戰效果。然而，隨著作戰信息化與網絡化的不斷推進，復雜的作戰網絡連接和作戰節點收集和傳輸信息時產生的信息冗余已經對作戰效果產生了重要影響。現有作戰效果評估方法由于沒有考慮到這些因素，其評估結果的準確性和可靠性無法得到保障。

為了解決這個問題，本文提出一種基于網絡協作度的作戰效果評估方法，通過研究作戰網絡連接度和信息冗余收益與代價，在建立網絡協作度模型的基礎上，給出作戰效果評估方法，最后完成仿真實驗并對評估結果進行分析。該方法全面考慮了影響作戰效果的各網絡因素，提高了作戰效果評估的準確性和可靠性。

1 網絡協作度概述

為了描述網絡協作所依賴的作戰網絡，這里引入簇的概念。簇是網絡中多個節點的集合，為節點間進行協作提供了空間，也為不同指揮員之同的協作決策提供結構支持。在網絡作戰中，良好的作戰效果需要通過信息優勢轉化為決策優勢來實現，而簇內節點的決策效果是基于網絡協作獲取信息得出的，因此，網絡協作和作戰效果之間存在聯系，如圖1所示。

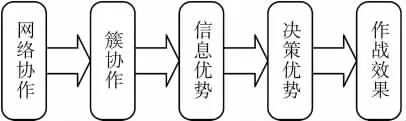
圖1 網絡協作對作戰效果的影響

本文用網絡協作度來描述網絡協作能力。網絡協作度是作戰網絡組織中的一組執行者通過相互連接實施相互作用的能力集合，這種度量將單個決策節點的決策行為和決策節點的相互耦合加到網絡中，從而影響網絡的性能［4］。網絡協作度既反映了網絡固有的特性，也反映了信息通過網絡時產生的效應。因此，本文對網絡協作度的分析從網絡連接度和信息冗余兩方面入手。

2 網絡協作度模型及作戰效果評估

2.1 網絡連接度計算

網絡連接的最大特征值和特征向量反映了網絡的特性，而特征值是一種衡量網絡連接距離的量。所以，距離函數是描述網絡連接度的有效函數。對于簇中給定的信息元素al，從信息源到目標節點的距離為dl，其連接度，其中wl反映了該信息元素的重要程度。若兩節點之間直接連接，則dl=1，kl=1；若兩節點之間無法連接，則 dl→∞，kl=0。

事實上，信息元素可能來自多個信息源，某個信息源也往往包含多個信息元素。在全連通網絡中，這些信息元素增加了網絡的最大特征值，提高了網絡的適應性和魯棒性。考慮到網絡中所有信息數的可達性，記X（k）為信息通過一定路徑到達目標節點可達程度的量（0＜X（k）＜1），假定所有信息元素具有同等重要性，則有：

2.2 信息冗余收益與代價計算

多信息源中的多重信息在網絡傳輸中，由于過多信息進入并與周圍節點實現信息共享，因此，存在信息冗余現象。信息冗余在增加評估的可靠性的同時，也會因為無用信息和信息超載而付出代價。

如果一個信息源非常可靠，其收益可以相當于多個不可靠信息源，所以需要對所有信息源提供信息的可靠性進行評估。如果信息源數對評估提供重要支持，則需要確定信息源數的權值。

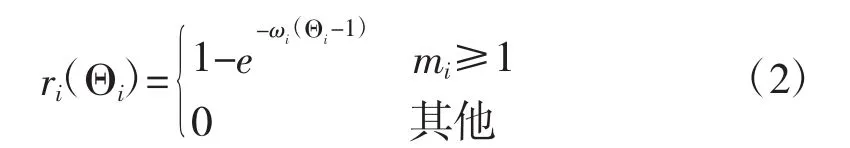
式中，參數ωi為信息元素ai的相對權重。當Θi=θi，1時表明該信息源是可靠的，其權重也相對較大，此時ri（Θi）→1。這個標準不僅度量了信息冗余的影響，也反映了信息源的充足程度。

從網絡全局來看，假設決策需求的可用信息元素總數為n，其中對簇起到關鍵作用的數目為C，則冗余收益為：

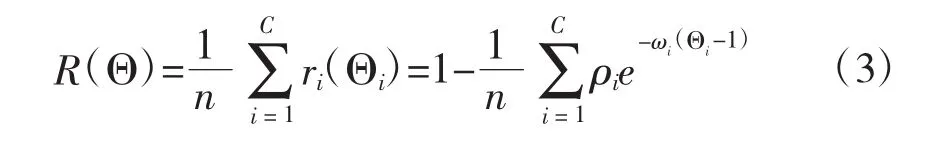
式中，當信息源數 mi≥1 時，ρi=1，否則為 0。

在簇中，提高協作能力所付出的代價是增加網絡連接、信息負荷過載、增加信息處理傳輸時間，造成信息元素以及傳輸時間的不確定。當不同信息源和傳感器的報告必須與一個完整作戰系統結合時，這些問題變得尤為明顯。造成不確定性的主要因素是無用信息和信息超載，因此，必須考慮到二者造成的代價。

在節點接收獲取信息并與簇內其他節點共享信息時，無用信息干擾了正常信息的獲取，具有直接的負面影響。其影響模型為：

式中，q為無用信息，ε為比例因子。無用信息是通過整個簇而不是通過一個單獨的節點來影響網絡的，這種情況下，相同信息元素提供X次無用信息與X倍信息元素提供一次的無用信息付出的代價相等。

當簇接收到過多有用信息時，容易產生信息超載，導致有用信息互斥。信息超載的代價模型可以表示為：

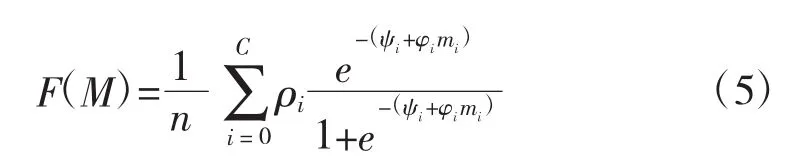
式中，mi為包含信息元素ai的信息源數量；ψi和φi為調節參數，其值取決于接受額外有用信息的結果；ρi為設定的系數，當 mi≥1 時，ρi=1，否則為 0。

2.3 網絡協作度模型

為了建立統一的網絡協作度模型，本文將基于信息可達性和信息冗余的協作能力作為評估網絡協作度的標準，前者評估了下層網絡結構的效果和系統本身具有的特性，后者度量了網絡運行的動力學特征。

為了標準化冗余收益，這里將信息可達收益X和冗余收益R進行合并。比率R（Θ）/X（k）表明一種相對關系，當 R（Θ）＜X（k）且 X（k）≠0 時，這個比率值不一定在［0，1］之間。如果用參數修改該比率，以避免零分母的出現，同時確保其值在［0，1］之間，則有：

式中，Q［R（Θ）/X（k）］為相對收益；參數 β＞0，確保其分母不為零；參數η＞0；參數β和η反映了冗余度和完整性的關聯程度；常量C1和C2保證組合標準取值在［0，1］之間。兩個邊界條件是 Q［0/0］=0 和 Q［1/1］=1，表明給定最大通道或取得最大冗余度產生了最大的組合評價。將邊界條件代入式（6），可得出C1和 C2。再將 C1和 C2的值與式（1）及式（3）帶入式（6），即可得出標準冗余收益［6］。

在標準化冗余收益的同時，考慮到所有的代價需要在有用和無用信息之間取得平衡，而有用和無用信息往往是相關聯的，其代價也會互相影響。因此，這里將二者線性加權，于是有：

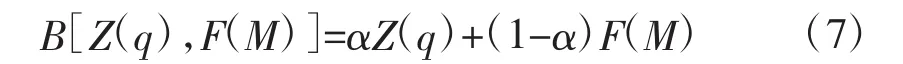
式中，α 為代價系數，取值范圍是［0，1］。

在網絡中，假定每一個簇采用邏輯連接的方式支持一個給定的任務。簇中的協作與簇中的信息流是相關的，過多或過少的信息流都會導致較差的網絡協作效果，反之，合適的信息流會帶來較高的協作效果。對于作戰網絡中的一個簇，針對具體的任務，將作戰網絡協作的收益和代價進行組合。這里采用二者的乘積作為標準，設定收益和代價為獨立事件，則網絡協作度模型為：

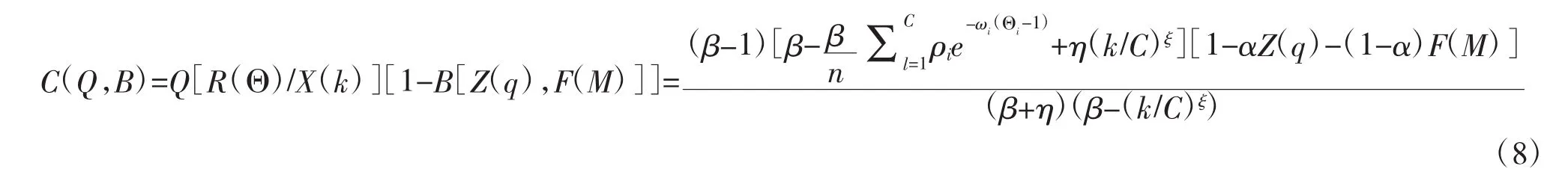
式（8）為網絡的協作度模型，它考慮了信息源、信息傳輸、網絡連接等帶來的冗余收益和付出的代價，并對收益和代價進行綜合。該模型的建立理清了網絡協作在影響作戰效果中的作用機理。

2.4 作戰效果評估方法

定義作戰效果為E（N），設網絡協作度和作戰效果之間的協作系數為，則：

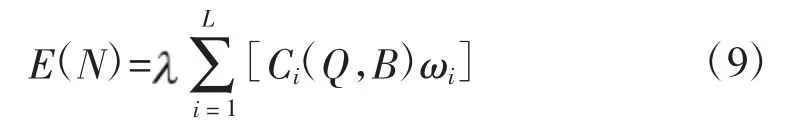
式中，L為網絡中簇的總數，ωi為簇的權重，信息在網絡中傳輸、處理后，進入簇決策中心，在取得信息優勢的情況下，決策中心指揮員對作戰組織的作戰行動進行決策，其作戰效果可通過式（9）計算得出。

3 仿真實驗及結果分析

假設紅方防空部隊對藍方戰斗機實施攔截，根據紅方協同作戰的經驗，其編隊組成為一輛指揮車（節點 10），兩門高炮（節點 1，2）和一門雷達（節點3）。由于紅方參與作戰的節點之間通信依靠網絡，節點之間的協同可借助網絡進行。紅方作戰節點獲取的信息通過網絡連接最終傳送到中心指揮所，這個過程如下頁圖2所示。

紅方編隊作戰節點1，2，3，10為信息源。確定藍方戰斗機的關鍵元素為距離、方位和高度，即C=3。設網絡的協作系數、無用信息、連接強度和信息源數為關鍵變量，有關的風險系數、反應邊界的η=1、β=2付出代價系數α=0.5、簇的數量L=4設定為非關鍵變量。本文采用Analytica軟件進行仿真，通過式（9）對各關鍵變量進行實驗，從而得出其對作戰效果的影響。

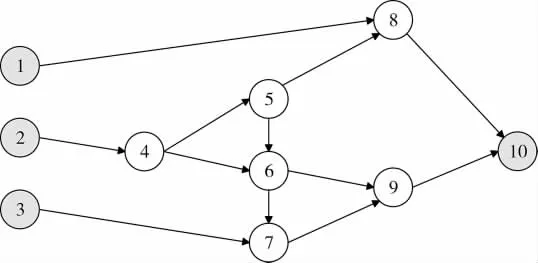
圖2 紅方網絡連接示意圖

1）協作系數對作戰效果的影響如圖3所示。

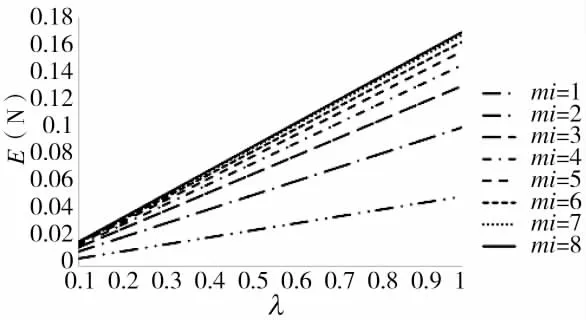
圖3 協作系數對作戰效果的影響

圖3表明，網絡的協作系數越高則作戰效果越好。同時，在信息源達到5個以上時，其數量的增加對作戰效果的增強逐漸趨于平緩。

2）無用信息對作戰效果的影響如圖4所示。

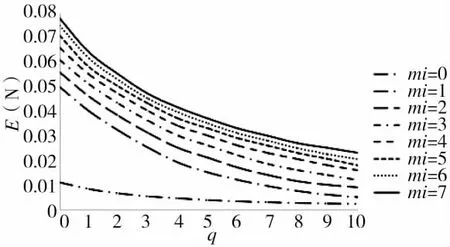
圖4 無用信息對作戰效果的影響

圖4表明，在信息源數量一定時，無用信息多意味著作戰效果差。在無用信息多時，信息源數量對于作戰效果的影響不明顯。

3）網絡連接度對作戰效果的影響如圖5所示。

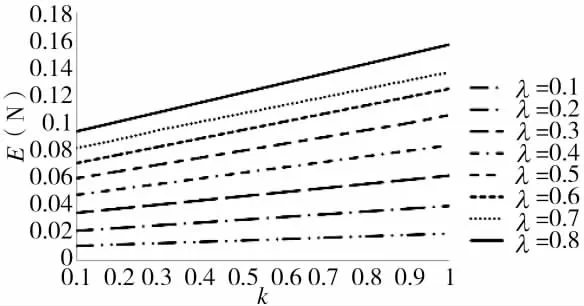
圖5 網絡連接度對作戰效果的影響

圖5表明，在協作系數一定的情況下，作戰網絡的連接度影響作戰效果，且協作系數越大作戰效果越好。在協作系數很小時，連接度對作戰效果的影響不明顯。

4）信息源數對作戰效果的影響如圖6所示。

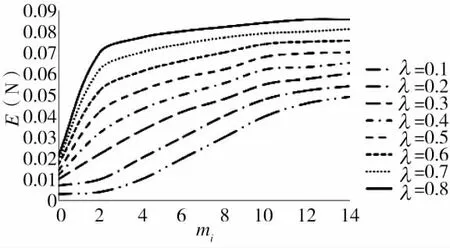
圖6 信息源數對作戰效果的影響

圖6表明，信息源數量的增加，導致了作戰效果的提升。在信息源數量很少的情況下，協作系數對作戰效果的影響幾乎呈線性關系。當信息源數量達到一定的值后，協作系數對提高作戰效果的影響不明顯。

4 結論

本文著眼于網絡化作戰中對作戰效果評估的問題，在計算網絡連接度和信息冗余收益與代價的基礎上，建立了網絡協作度模型，并基于該模型提出作戰效果評估方法，最后進行仿真實驗。結果表明：在網絡可靠性一定時，信息源達到一定數量可以消除無用信息的影響，并且對協作系數不敏感。同時，網絡連接度的增加可以顯著提升作戰效果。該方法充分考慮了影響作戰效果的各個網絡因素，能夠準確地對作戰效果進行評估，為指揮人員感知戰場態勢、改進作戰計劃提供了可靠依據，在網絡化作戰中具有重大應用價值。