度量信息系統的屬性約簡

史　嬋

(西安郵電大學 通信與信息工程學院， 陜西 西安 710121)

用于不精確和不確定數據信息分析的粗糙集理論[1],作為一種有效的知識發現與獲取工具，倍受關注[2-8]。粗糙集理論以數據庫為基礎，兩者發展關系密切。早期信息系統的屬性取值域有限，只探討等價關系。隨著數據庫的深入分析，信息系統的取值域及其論域上的二元關系也不斷擴展。結合其他理論，涌現出許多新的信息系統。例如取值為區間的區間值信息系統[9-10]，取值為集合的集值信息系統[11-12]，取值在特定區間內的連續值信息系統[13]等。基于實際生活中的優勢關系，信息系統被擴展為序信息系統[14-15]。基于模糊集理論，信息系統又被擴展為模糊信息系統[16-18]。不過，這些信息系統都無法直接處理信息表中的多維數據。

其實，對于信息系統，除了討論其取值域以及二元關系之外，還可以考慮從取值域的代數結構和幾何結構進行分析。如將所有屬性值限定在同一個度量空間，那么，在引入度量之后，所得度量信息系統則可解決信息表中多維數據的處理問題。此外，度量信息系統更是部分信息系統的推廣，這些信息系統不過是度量信息系統在合適度量下的特例；在相同的信息表中，引入不同度量，還可從不同角度獲取不同知識。

屬性約簡是信息系統理論研究的核心問題之一[8]，即在保持知識庫分類能力不變的條件下，刪除其中不相關或不重要的屬性，從而簡化知識的表示。本文將基于度量空間研究信息系統的屬性約簡與特征描述。

1　度量信息系統

將度量引入信息系統，考慮度量信息系統上論域子集在相似關系下的上、下近似。

定義1[19]稱(T,d)為度量空間，其中

d:T×T→

是一個非負函數，且對任意x,y,z∈T,滿足

(1)d(x,x)=0,

(2)d(x,y)=d(y,x),

(3)d(x,z)≤d(x,y)+d(y,z)。

定義2稱信息系統(U,A,F,T)是一個度量信息系統，若(U,A,F)是信息系統，其中

U={x1,x2,…,xn},A={a1,a2,…,am},F={fl:U→T,al∈A},

且(T,d)為度量空間。

定義3設(U,A,F,T)是一個度量信息系統。對于任意的ε>0,B?A，定義二元關系

并記

其中,ε稱為系統誤差。

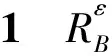
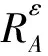
例1某市內行政區規劃的部分數據如表1所示。對象集U={x1,x2,x3,x4,x5}是5個住宅區。屬性集A={a1,a2,a3,a4}是規劃擬建的4個公園。屬性值表示各住宅區相對于特定公園的距離(單位：km)。例如，第1列表示以公園a1為笛卡爾坐標系的坐標原點，住宅區xi(i=1，2，3，4，5)所在的位置。那么，(U,A,F,T)即是度量信息系統。其中:fl∈F，如f1(x1)表示對象x1在屬性a1下的屬性值，即f1(x1)=(-1，0);T=2為二維平面，d代表歐氏距離，即對任意(x1,y1),(x2,y2)∈2，有

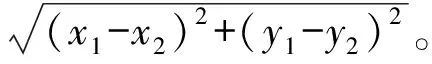
表1　度量信息系統實例

當ε=2，B=A時，按照定義3，可以求得

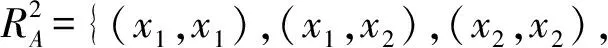
即若以與住宅區相對距離在2 km之內為準則，建設4個公園，則住宅區x1和x2將被劃歸同一個居住帶,亦即小區x1和x2的居民距公園遠近或游玩的便利程度相當。

定義4設(U,A,F,T)是一個度量信息系統，X?U,ε>0,稱

為X關于B的ε-下近似，稱

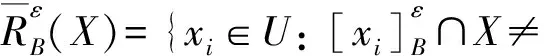
為X關于B的ε-上近似。

例2設(U,A,F,T)是例1提到的度量信息系統。取X={x1,x5}，由定義4可知

定理1設(U,A,F,T)是一個度量信息系統，任給ε>0，X,Y?U,則X和Y關于B的ε-下近似與X和Y關于B的ε-上近似具有性質

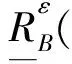
(1)

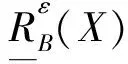
(2)

(3)

(4)

其中,┐X=U-X。

證明僅證明式(3)中的

其余類似可證。

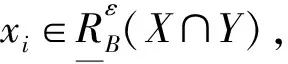
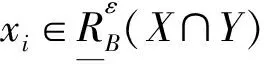
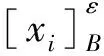
故有等價式

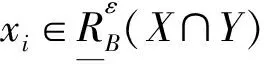
故待證等式成立。

2　度量信息系統的屬性約簡

針對度量信息系統的屬性約簡問題給出約簡準則，并利用辨識矩陣進行屬性約簡。

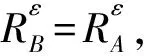
定義6設(U,A,F,T)是一個度量信息系統，記

Dε(xi,xj)={al∈A:d(fl(xi),fl(xj))>ε},D=[Dε(xi,xj)](xi,xj∈U),

稱Dε(xi,xj)為xi與xj間的辨識集，D為度量信息系統的辨識矩陣。

定理2設(U,A,F,T)是一個度量信息系統，則B是ε-協調集,當且僅當Dε(xi,xj)非空時，B∩Dε(xi,xj)也非空。

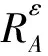
例3表1所對應的辨識矩陣D可表示為

其中

D1={a1,a2,a3,a4},D2={a1,a2,a4},D3={a2,a3}。

取B1={a1,a3}，由定理2可知，B1為2-協調集。因B2={a1}?B1和B3={a3}?B1不滿足定理2的條件， 故其不是2-協調集。除B2和B3外，B1再無其他非空真子集，故由定義5知，B5={a3,a4}和B1={a1,a3}為2-約簡。另外，在上述矩陣中亦可以觀察到B4={a2}，也是2-約簡。

3　度量信息系統的屬性特征

設(U,A,F,T)是度量信息系統，給定ε>0,B={Bk:k≤l}是所有ε-約簡構成的集合。記

則稱C為(U,A,F,T)的核心屬性集，K為(U,A,F,T)的相對必要屬性集，I是(U,A,F,T)的絕對不必要屬性集。

定理3設(U,A,F,T)是一個度量信息系統，則有等價命題

(1)a∈C；

(2) 存在xi,xj∈U，使得Dε(xi,xj)={a}；

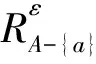
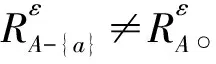
定理4設(U,A,F,T)是一個度量信息系統，則成立命題

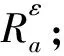
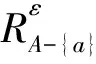
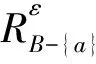
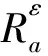
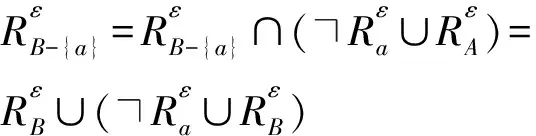
故a不在任何ε-約簡中，所以a∈I。

(2) 結合命題(1)，由定理3及C，I和K的定義,即可知命題(2)顯然成立。

例4分析例1給出的度量信息系統。由例3知，{a1,a3}，{a3,a4}，{a2}為該度量信息系統的全部ε-約簡，故由C,I和K的定義知

C=?，K={a1,a2,a3,a4}，I=?。

結合實際得到的屬性約簡結果表明,為了節約地皮同時保證居住帶不變，可以不用建設4個公園，只需建設公園a1,a3或者只需建設公園a3,a4或者只需建設公園a2。同樣可以保證同一居住帶居民的休息娛樂場所。

4　結語

通過結合度量空間，改變信息系統的取值域，提出度量信息系統。針對度量信息系統，給出了屬性約簡的判定定理、利用辨識矩陣求解約簡的方法以及3種屬性特征的等價刻畫。

度量信息系統在一定程度上是經典信息系統及連續值信息系統的推廣，本文考慮的是沒有決策的信息系統，關于度量信息系統上的決策問題還可另行討論。在信息系統上引入度量，不僅為以后利用鄰域概念等討論屬性間的依賴關系創造了條件，還可以研究信息系統之間的同構關系，由此對信息系統作分類，便于信息系統的統一。