高超聲速飛行器非線性巡航控制器設計

趙宏宇, 黃得剛, 何啟志, 章衛國

1.兵器工業集團 航空彈藥研究院, 黑龍江 哈爾濱　150036;2.西北工業大學 自動化學院, 陜西 西安　710129;3.陜西省飛行控制與仿真技術重點實驗室, 陜西 西安　710129

我國著名科學家錢學森于1946年首次提出了高超聲速(Ma>5)的概念,能夠超過這個速度的飛行器包括導彈、火箭和航天飛機,而在大氣層內飛行的飛行器還未能以該速度巡航。從戰略偵查的角度來講,如果偵查飛行器具備了這種高超聲速巡航能力,那么其隱身性能將不再重要。速度是新的隱身,為應對未來數十年可能產生的威脅與挑戰,提高飛行速度十分必要。正如隱身技術改變今日的戰場環境一樣,速度將改變未來的戰場規則和作戰模式。

高超聲速飛行條件下,氣動熱彈性為主要的物理問題[1-4]。氣動熱彈性現象的存在將會引發飛行器的外形發生變化、機體彈性形變、彈性振動等問題,也引入了動態不確定因素[5],這種現象的存在已經在美國SR-71偵察機上得到了驗證[6],另外這種氣動熱彈性引起的彈性振動是一種極具破壞力的氣動彈性不穩定現象,劇烈的震顫將會對飛行器壁板結構的疲勞壽命甚至飛行器的飛行性能產生十分不利的影響,甚至會導致飛行器在短時間內解體[7]。再者,相比于亞聲速和超聲速飛行器來說,高超聲速飛行器在其控制問題上相對復雜[8],原因在于:①以X-43A和X-51A為代表的新一代高超聲速飛行器,普遍采用吸氣式沖壓發動機為高速飛行推進系統的設計方案,研究表明,對于這一類飛行器來說,推進系統與機身之間存在嚴重的耦合效應;②高超聲速飛行器與亞聲速/超聲速飛行器相比有許多不同的飛行特性,有的方面目前還無法完全掌握,使得高超聲速動力學呈現強不確定性。高超聲速飛行器的不確定性主要來源于氣動特性、氣熱特性和大氣干擾三方面[9-10];③高超聲速飛行時,需要對飛行包線進行保護,一旦偏離飛行包線就會出現“熱阻現象”,這種熱現象顯著降低飛行器的整體性能,最直接的方法對航跡角進行高精度控制[11];④隨著飛行速度的不斷提高,對飛行器的實時性要求越來越苛刻,對于以5馬赫速度飛行的飛行器,每延時1 ms,就會產生1.5 m的誤差。因此,控制系統的快速性也是一個需要解決的問題[12];⑤目前大量文獻中的高超聲速飛行器的控制問題一般只考慮縱向控制,如果加上橫側向的控制會使得問題變得更加復雜[13],因此,橫側向的控制對縱向控制的影響需要予以考慮。

對于高超聲速飛行器的控制問題,國內外已有不少相應的研究成果,如魯棒控制[14-16]、Backstepping控制[17-18]、滑模控制[19]、基于優化方法的控制[20]、動態逆控制[21]等,雖然這些先進控制方法都取得了不錯的控制效果,但是對于上述給出的高超聲速飛行器獨有的特性來說,這些控制方法中并沒有給予充分的考慮。本文以高超聲速飛行器在30 km處以6馬赫定速巡航飛行為研究背景,提出一種指令濾波積分動態面backstepping滑模控制方法,該方法首先利用一個二階指令濾波器解決傳統backstepping方法中存在的“計算膨脹”問題;其次,引入滑模控制解決存在匹配不確定性和外界擾動的控制問題,采用帶調節函數的自適應backstepping方法來處理存在匹配不確定性的控制問題。為了降低引入滑模控制帶來的抖動,本文利用高階滑模控制的思想,在傳統backstepping方法上增加了一個虛擬控制狀態方程,將系統的最終輸出作用在一個積分器上,從而達到降低滑模抖動的目的。這樣所設計的控制器不僅可以解決匹配和非匹配不確定性以及外界擾動的問題,而且還可以降低引入滑模控制帶來的抖動;然而引入一個附加虛擬控制方程會導致傳統backstepping方法的“復雜性膨脹”問題,即隨著系統階次的增加,控制方法設計過程中的中間虛擬變量導數的計算將會維持不住[22],而動態面方法可以有效解決這一問題[23]。最后,本文從理論上證明了所提方法的全局穩定性,并同時通過仿真實驗驗證了該方法的魯棒性和有效性。

1　高超聲速飛行器6自由度非線性數學模型

本文采用高超聲速飛行器的6自由度非線性模型作為研究對象

(1)

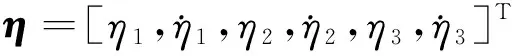
力和力矩的表達式為[16,26,27]

(2)

nA=nmrc+XcgY

i=1,2,3

式中

(3)

j=T,M,L,D

i=1,2,3

相關氣動系數具體數值參見文獻[7,15-16,18,24,26]。

為了便于實際應用中的控制器設計,需要將(1)式按照縱向和橫側向解耦的形式進行整理變形,可得縱向數學模型為

(4)

式中

fα=-tanβ(pcosα+rsinα)+

gα=1

fγ=

fh=0

gh=V

符號mA(δe)和L(α)表示俯仰力矩和升力的表達式中含有升降舵和迎角變量,可以利用相應的氣動關系導出所需的控制變量。同理橫側向的數學模型為

(5)

式中

由于fμ書寫過長,此處不在給出,按照(1)式中的傾斜角μ的微分方程可以很容易的導出fμ的具體表達式。另外符號lA(δa)和nA(δr)表示滾轉力矩和偏航力矩中含有副翼δa和方向舵δr變量,利用氣動特性可以導出相應的控制關系式。同樣的方法可以得到發動機推力的數學模型為

(6)

式中

至此,根據(4)～(6)式的形式,很容易實現縱向為h→γ→α→q→δe的控制,橫側向為μ→p→δa和β→r→δr的控制,以及空速為V→Φ的控制。同時根據非線性數學模型的特點,還需要引入各種交叉耦合的影響。下面根據(4)～(6)式來設計6自由度非線性數學模型的控制器。

2　非線性控制器設計

2.1　二階指令濾波

本文采用二階backstepping控制方法,這樣推導控制律時需要計算期望輸入的二階導數,故這里采用二階指令濾波。假設濾波器的傳遞函數如下

(7)

式中，ζ為阻尼比,ωn為濾波器的自然頻率,增加ωn可以使得閉環控制系統的解任意精度接近求解解析導數的閉環系統的解[28-29]。

2.2　積分backstepping控制

為了方便說明問題,本文僅以推導最內環的俯仰角速率控制器的設計過程為例,其它控制環的設計過程類似,此處不再贅述。假設俯仰角速率狀態變量為x1,實際升降舵控制變量為x2,引入的虛擬控制u,則有

(8)

式中

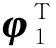
首先定義位置誤差為

z1=x1-zd

(9)

式中，zd為狀態x1期望的輸入指令信號,則

(10)

定義

z2=x2-α1

(11)

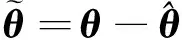
(12)

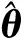
定義Lyapunov函數

(13)

并定義

(14)

式中，Γ是正定矩陣,V1對時間求導可得

(15)

令

(16)

τ1=φ1z1

(17)

從而可得虛擬控制量α1為

(18)

式中，c1>0,并將α1通過一個一階濾波器

(19)

這樣可以利用(19)式直接得到α1的一階導數,無需再計算α1的解析一階導數,因為隨著系統階數增加,α1各階導數的解析形式十分復雜。

再對(11)式求導可得

(20)

(21)

如果z2=0,則V1≤0,為此需要進行下一步的設計

定義Lyapunov函數

(22)

對V2求導可得

(23)

由此可見,當采用動態面后,推導自適應backstepping方法的第二步時,彈性模態部分也被包含在中間虛擬變量α1中,同樣無須計算彈性模態的導數,降低了backstepping方法的復雜性。

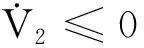
(24)

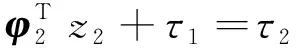
(25)

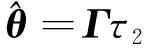
(26)

整理可得最終的虛擬控制量u為

(27)

從而可得

(28)

由(27)式可見,相比于傳統的backstepping方法,所得最終控制律的形式十分簡潔。

以上可稱為標稱系統的控制律設計,可以記為ueq=u,為了保證系統對外界的擾動和匹配不確定性的魯棒性,設計切換控制律usw為

usw=-εsgn(s)-ks

(29)

式中，s為

s=λ(z1+z2)

(30)

式中，ε>0,k>0,λ>0,sgn(·)為符號函數,從而系統總的輸出量為

U=ueq+usw

(31)

將(31)式的結果積分后恰為模型所需的升降舵控制輸入x2,該指令濾波積分backstepping滑模控制的結構方框圖如圖1所示。

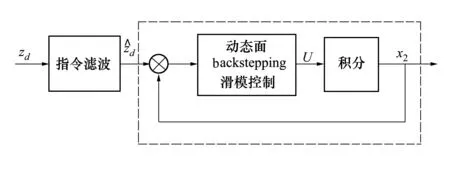
圖1　指令濾波積分動態面backstepping滑模控制結構圖

3　控制器的穩定性分析

為了分析控制器整體的穩定性,首先分析動態面Backstepping控制的穩定性,為此給出如下假設1和定理2。

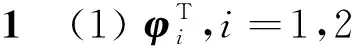
定理1考慮非線性系統(8),給定非線性特性和不確定性滿足假設條件1,則對于任意初始狀態,存在面增益系數ci,i=1,2和時間常數ε1使得動態面backstepping控制器能夠保證系統狀態收斂到原點。

證明略,詳細證明過程參見文獻[22]。

得到動態面backstepping控制的穩定性之后,需要繼續證明指令濾波動態面積分backstepping滑模控制器的穩定性。不失一般性,假設圖1中的虛線內為一般非線性控制系統為

(32)

式中，y為實際控制輸入經過指令濾波器后的控制量,同時將(7)式指令濾波器轉化為狀態空間形式

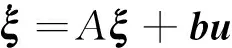
y=hξ,ξ∈Rq,u∈R

(33)

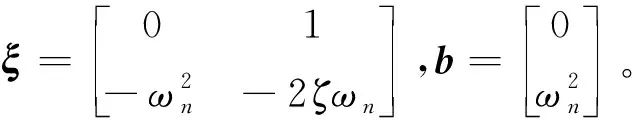
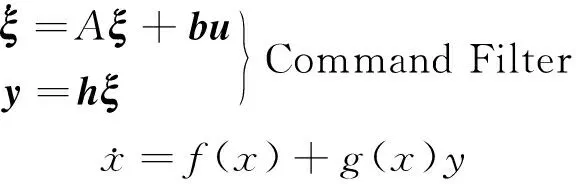
(34)

假設當y=0時,系統(32)在平衡點x=0處全局穩定,且存在Lyapunov函數V(x)滿足

(35)

式中，W(x)正定。此時需要解決系統(34)是否為全局穩定的問題,該問題可以轉化為鎮定系統(33)不影響系統(32)穩定性的問題。

假設2系統(A,b,h)為反饋正實系統,即對于系統(33),存在線性反饋變換u=Kξ+v,使得(A+bK)是Hurwitz的,且存在p>0,Q≥0滿足

(A+bK)TP+P(A+bK)=-Q

Pb=hT

(36)

引理設V(x)為系統(32)的Lyapunov函數,且滿足式(35)。如果(A,b,h)是反饋正實系統,那么系統(34)的Lyapunov函數為

Va(x,ξ)=V(x)+ξTPξ

(37)

且控制律

(38)

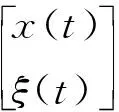
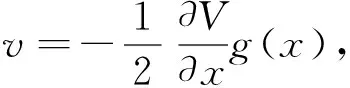
因為Va徑向無界,且Va的導數為負半定,故x(t)和ξ(t)全局有界。此外LaSalle定理保證了x(t)和ξ(t)收斂到Ea的最大不變集Ma上。為了說明鎮定系統(33)不影響系統(32)的穩定性,首先證明圖1中虛線框內的積分動態面backstepping滑模控制器的穩定性。

定理2對于系統(8),采用控制律(31)可以使系統(8)漸近穩定。

證明:根據等效控制理論可知,為使設計的控制律U穩定系統(8),需滿足滑模穩定條件[31],則定義Lyapunov函數

(39)

將其對時間t求導可得

(40)

整理可得

(41)

定理3如果y=0時,系統(32)在平衡點x=0處為全局漸近穩定,那么系統(33)在平衡點x=0,ξ=0處也為全局漸近穩定。

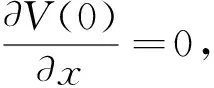
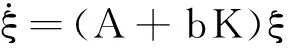
定理4如果內回路控制為全局漸近穩定,那么外回路控制亦為全局漸近穩定。

證明假設內回路俯仰角速率控制系統的跟蹤誤差為eq,針對外回路的迎角控制,需要考慮內回路對外回路的影響,為此選取Lyapunov函數為

(42)

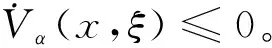
(43)

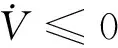
(44)

即內環俯仰角速率若為全局漸近穩定,那么其外環的迎角控制也為全局漸近穩定。由此易知,外環的航跡角控制和高度控制,各個回路均為全局漸近穩定;同理可知,橫側向控制系統亦為全局漸近穩定。至此,證明了所設計的控制系統能夠保證高超聲速飛行器6自由度非線性數學模型的穩定性。

4　仿真計算驗證

臨近空間指的是20～100 km的空間范圍,本文假設高超聲速飛行器以6馬赫的速度飛行,飛行高度為30 km,該高度屬于平流層,臨近空間平流層的氣流運動相對穩定,氣流以水平運動為主,根據NASA給出的35 km以內的平均風速隨高度的變化曲線示意圖可知30 km處的風速平均為14 m/s左右[33],故本文利用Matlab中的Dryden風場模型,在高超聲速飛行器過程中加入14 m/s的常值風干擾,并將文獻[7,14-15,17,21]給出的所有氣動數據攝動+20%,以此來驗證所提方法的控制效果。

初始條件設定為

x0=[h,V,γ,μ,α,β,p,q,r]=[30 000,5 859.7,0,

0,0.447 88°,-0.1,0,0,-0.082]，仿真時間設定為50 s,以高度30 km定高飛行時,6馬赫對應的飛行速度為5 859.7 m/s,仿真結果如圖2所示。

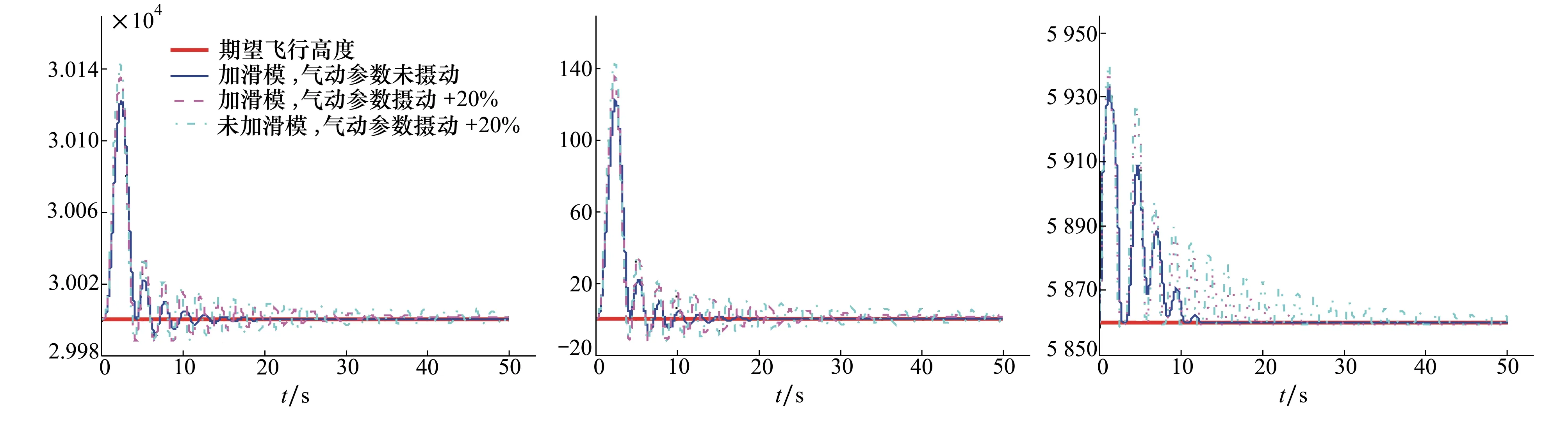
圖2　高度跟蹤　　　　圖3　高度跟蹤誤差　圖4　速度跟蹤

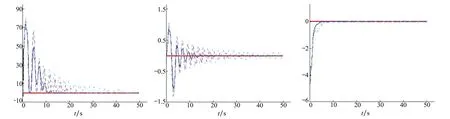
圖5　速度跟蹤誤差　　　　圖6　航跡角跟蹤　圖7　側滑角跟蹤

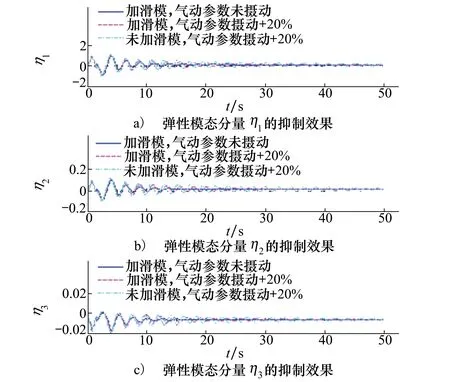
圖8　彈性模態的分量

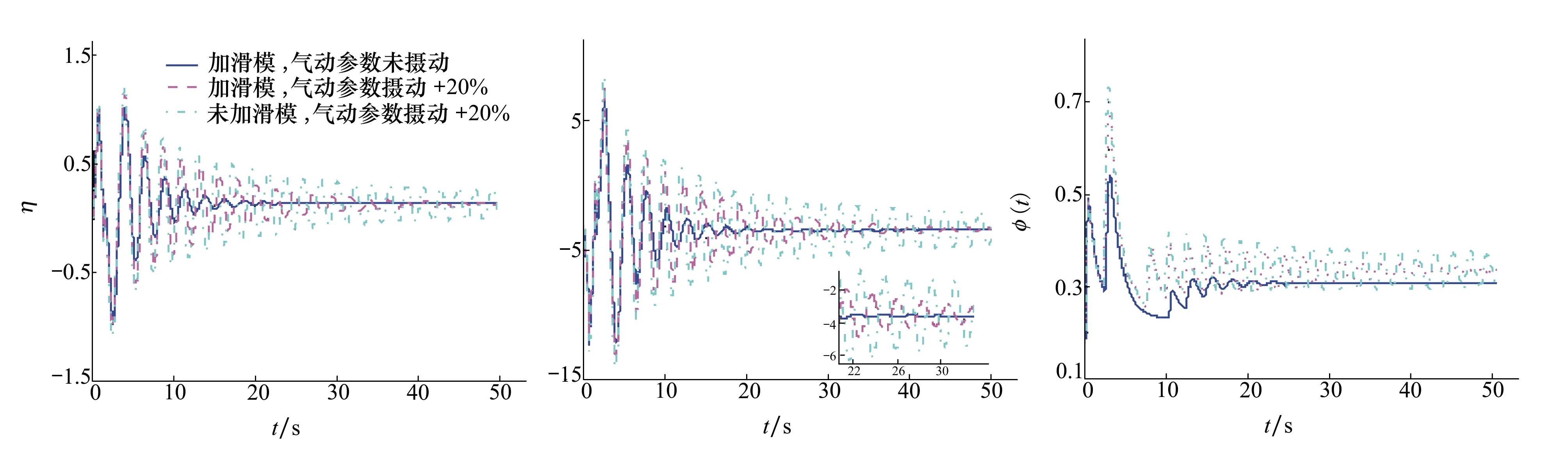
圖9　彈性模態分量的疊加　　　圖10　升降舵偏轉　圖11　燃料當量比

利用文獻[16, 24]中給出的氣動熱引起的彈性振動表達式得到的仿真結果如圖8和9所示,圖8給出了彈性模態的3個分量,圖9給出彈性模態3個分量的疊加結果,將這三者疊加后分別作用在升力、阻力、俯仰力矩和推力力矩上,以此來模擬氣動彈性熱對高超聲速飛行器定速巡航時的影響。根據仿真圖8和圖9可知,當所有氣動參數攝動+20%時(彈性模態參數同樣攝動+20%),由于迎角、升降舵和彈性模態之間的耦合影響,使得舵面偏轉加劇的同時,彈性模態分量的變化也隨之加劇,從而使得疊加后的彈性模態振動加劇,顯著影響高度跟蹤的精度;從圖2～圖7的仿真結果可以發現,氣動參數未攝動的情況下,高超聲速飛行器可以很好實現高度的跟蹤、航跡角的跟蹤、側滑角的跟蹤和速度的跟蹤控制,然而當所有的氣動參數攝動+20%之后,去掉滑模控制的控制效果顯然要差,這樣從實驗的角度說明了滑模控制在處理匹配不確定性和外界擾動問題的優越性。然而,即便是所有的氣動參數攝動+20%之后,本文所提控制方法能夠保證系統的全局穩定性,而且跟蹤誤差成漸近收斂的趨勢。另外,根據圖6的實驗結果可知,航跡角約在1°范圍內進行波動,系統不會出現“熱阻現象”。再者,在設定的50s仿真時間內,升降舵的偏轉如圖10所示,該實驗結果表明,在飛行器高超聲速飛行時,升降舵的偏轉角度在規定的范圍內偏轉,同時觀察圖10右下方的小圖,該小圖表明所設計的控制器沒有因為引入了滑模控制而產生抖動現象;值得注意的是在仿真開始時,舵面的調整幅度較大,原因在于氣動熱彈性模態引起的振動較大,需要利用升降舵的偏轉對其進行抑制。而在參數未攝動的情況下,隨著氣動熱彈性振動趨于平穩狀態,升降舵的偏轉也趨于穩定狀態,收斂值約為-4°,而當升降舵偏轉角度出在5°偏轉角的范圍內時,飛行器高超聲速飛行的阻力會顯著降低[25],適合高超聲速飛行;在參數攝動+20%的情況下,升降舵偏角同樣可以收斂到5°偏轉角的范圍內,同樣滿足高超聲速飛行的條件;最后,利用文獻[16]中給出的燃料當量比的計算公式,可以得到相應的燃料當量比的仿真結果,如圖11所示,根據該仿真結果可知,燃料當量比滿足其約束范圍。

5　結　論

高超聲速飛行器在30 km處以6馬赫定速巡航時,不僅存在氣動參數的不確定性和外界大氣擾動,而且由于高超聲速飛行導致的氣動熱彈性問題較為嚴重,這種彈性振動對飛行器的穩定性的影響十分顯著,處理不好這種彈性振動會使得高超聲速飛行器變得不可控,甚至出現飛行器解體的危險,為此,本文提出了一種指令濾波積分動態面backstepping滑模控制器,仿真結果表明,所提出的控制方法不但可以有效地應對引言中提到的高超聲速飛行器獨有的一些飛行特性問題,而且可以較好地完成高超聲速飛行器6馬赫定速巡航的飛行任務。