結合小波框架與TV的一個正則化方法

劉 通,崔卓須

(武漢大學數學與統計學院,湖北武漢 430072)

1引言

從模糊的、有噪聲的或者部分觀測圖像做圖像恢復可以看成一個反問題的應用,數學表達式可以寫成如下形式

其中x,y∈Rm×n分別代表著原始圖像與觀察到的圖像,?是方差為σ2的高斯噪聲.A是從Rm×n映射到Rm×n的線性算子,在圖像的去卷積過程中,取A為卷積算子.在反問題中,A是不可逆或者有很大條件數的病態的算子.由于噪聲的存在,完全恢復圖像是不可能的,所以只能使用正則化方法尋找近似解.修改后的模型為

其中αR(x)就是包含著解的先驗信息的正則項,α是正則化參數.

我們在正則項中使用R(x)=|Dx|,其中D取局部差分算子.這個正則項是非光滑非可分的,一個自然的想法是使用光滑化的l1范數逼近,基于全變分(TV)的圖像恢復經常使用這種方法.而TV有利于保持圖像的銳利和物體的邊界,而且在恢復圖像過程中保住分片光滑的物體[1,2].但是同時TV也有一些缺點,比如會在平坦區域產生階梯現象造成圖像細節丟失等.

在圖像恢復過程中另一個重要性質就是圖像的稀疏表示.最好的稀疏性由L0范數生成,但L0范數導致了NP困難問題,所以我們使用了L1范數做逼近.利用小波框架表示圖像則有利于保證稀疏性的存在[3,4].本文將TV和小波框架兩種正則化模型結合在一起以保持各自的優點.在正則化模型的使用過程中,用ADMM算法以達到快速穩定的目標.在之后的數值實驗中,將看到新方法提高了原有的TV和框架模型的效果[5,6].

2 基于ADMM的圖像恢復模型

2.1 兩種圖像恢復模型

TV去噪可以看做最有效和最難計算的幾種方法之一.為了去除它的缺點,近年已經發展出了原對偶方法,FTV d和增廣拉格朗日方法等[7].在這里將TV方法應用于原問題.

對于圖像x∈Rm×n,用符號? 表示離散階梯算子從Rm×n映射到Rm×n×Rm×n.即?x=(?1x,?2x),在這里

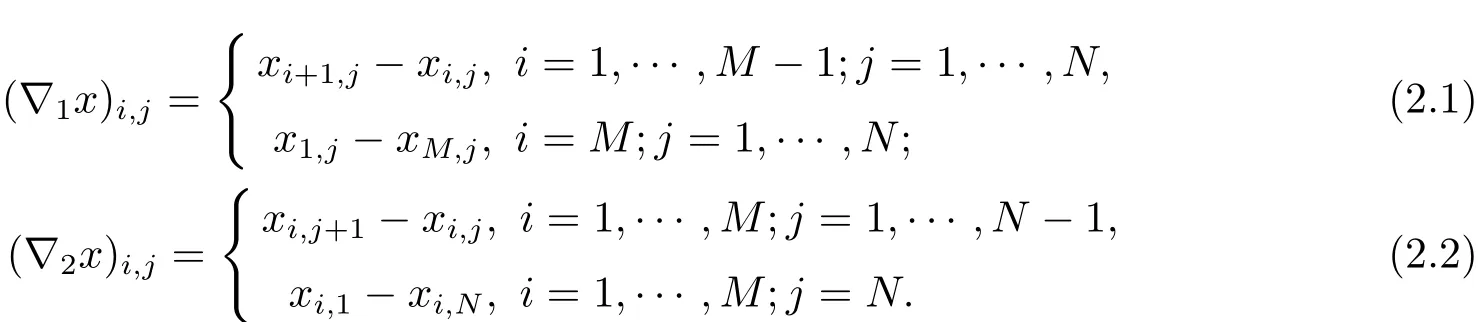
由于使用的是L1范數,定義 ∥x∥TV= ∥?x∥1=|?1x|+|?2x|,稱為各向異性,那么在應用ADMM算法時會有兩個正則化項.此時問題變成

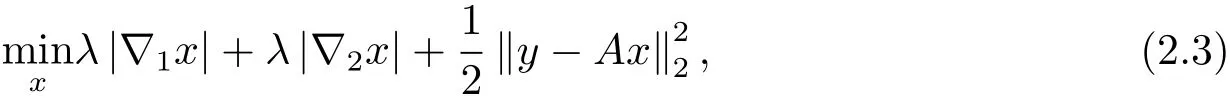
這里取λ>0作為正則化參數,用來平衡三項的最小化取值.把該最小化問題變成約束最優化問題

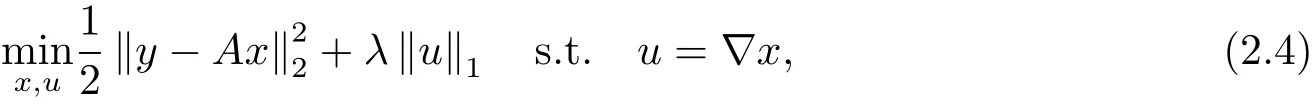
再得到增廣拉格朗日函數

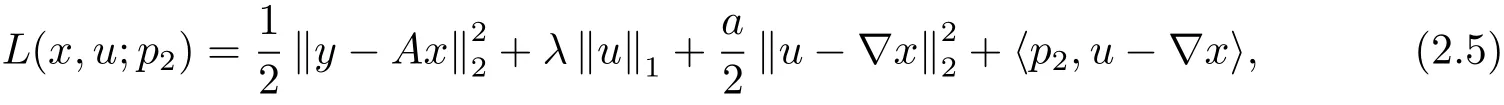
這里 p2=(p2,1,p2,2)∈RM×N×RM×N為拉格朗日乘子,作用是防止λ>0在計算中趨向于無窮大.

類似的,取框架分解算子W,那么可以把原反問題寫成最小化問題

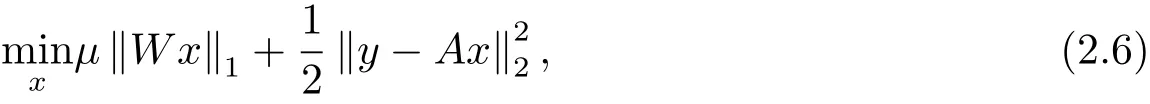
這里取μ>0為正則化參數.把該最小化問題變成約束最優化問題

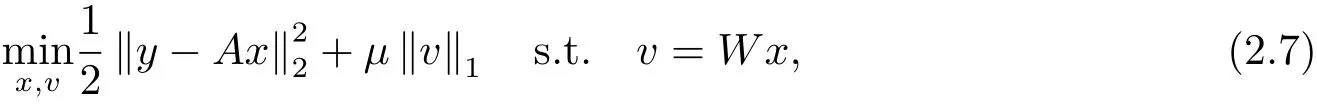
再得到增廣拉格朗日函數

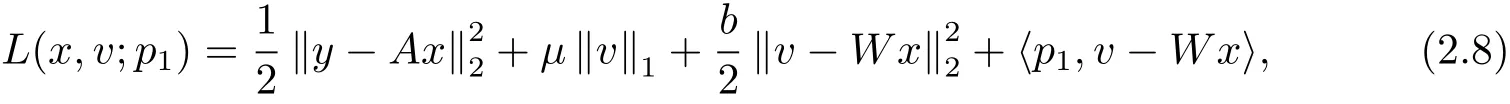
這里p1∈RM×N為拉格朗日乘子,作用是防止μ>0在計算中趨向于無窮大.

2.2 結合兩種模型的圖像恢復

結合兩個模型,在用小波框架作為第一步求出一個最優解之后,把該最優解作為一個初始值帶入到第二個模型算法之中做第二次運算,以求出更好的解.于是得到新的方法如下

1.1:輸入初始值y,A,μ>0,b>0,x0=y,v0=Wx0,=0;

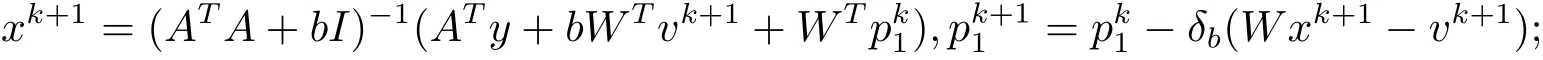
1.3:輸出xn;

2.1:輸入新的初始值y,A,λ>0,a>0,xn=y,u0=?xn,=0;

選定的停機準則為

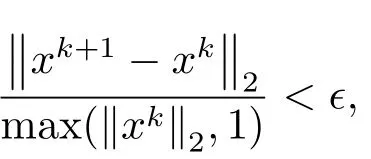
其中?>0是一個給定的值.

3 數值試驗結果與分析

3.1 圖像去模糊結果及分析

圖1:去模糊效果對比圖

表1:去模糊時的峰值信噪比

3.2 圖像去噪聲結果及分析

在去噪聲實驗中,δa=0.5,δb=1,μ =5×e?3,λ =5×e?3,a=b=1;作為對照,TV部分λ=0.01,δa=1和a=1;框架對照部分μ=0.01,δb=1.5和b=1.實驗結果在圖2中顯示,峰值信噪比見表2.

圖1:去噪聲效果對比圖

表2:去噪聲時的峰值信噪比

4 結語

在帶噪聲圖像恢復后的背景和草地的細節中,能夠很明顯地看到本文方法的優勢在于保持了更多的細節信息.從PSNR的數據中,可以看到從模糊圖像和帶噪聲圖像的恢復中,本文的方法得到了更好的恢復結果.

針對圖像從模糊和噪聲中恢復的問題,本文結合了小波框架和TV模型,提出了新的L1正則化模型,并且應用ADMM算法來結算這個新的模型.數值實驗的結果顯示本文的方法在圖像恢復過程中保留原始圖像的邊緣信息和細節上具有優勢.于是本文的方法尤其適合恢復帶有很多紋理細節的圖像信息.在實驗得到的PSNR數值結果佐證了這個判斷.而這種將兩種模型結合的思想可以應用在更多的場景之中.在今后的研究中可以應用同樣的思想,將不同的算子組合來恢復具有不同的幾何信息和不同噪聲的圖像.