一類HIV傳播人群的非線性動力學模型

馮依虎, 汪維剛, 莫嘉琪

(1. 亳州學院 電子與信息工程系, 安徽 亳州 236800； 2. 合肥幼兒師范高等專科學校, 合肥 230011；3. 安徽師范大學 數學與統計學院, 安徽 蕪湖 241003)

0 引 言

人體免疫缺陷病毒(HIV)的傳播嚴重威脅人類的健康. 目前, 利用動力學方法研究HIV的傳播已得到廣泛關注[1-3]. 該方法先建立反映其基本現象的微分模型, 再用解析方法求出模型的近似解, 然后將研究結果與實際觀測數據作為依據, 從醫學、生態學、數學等角度考察其動態規律. 本文考慮一類非線性動力學HIV傳播模型, 利用微分系統解析理論給出這類HIV的傳播規律.

非線性問題能代表自然界較普遍的復雜現象, 在應用數學中應用廣泛, 目前已有很多可行的近似求解方法[4-31]. 本文利用一個簡單、有效的方法考察HIV傳播的傳染人群非線性微分動力學模型[1], 通過對其進行定量和定性分析, 給出調解感染者人數和易感者人數的分布規律.

1 HIV傳播動力學微分系統

考慮如下更廣泛的一類HIV傳播人群的生態動力學非線性微分系統模型：

其中:u(t)為在HIV傳播區域內的感染者人數;v(t)為易感者人數;t為時間；e≥0為易感者的出生率;a,b,c,h為非負常數. 在系統(1)-(2)中,a(u+v)v項表示感染者與易感者因“交感”而導致的患者增加速度, -hu項表示由于患者死亡而導致的患者減少速度, -eu項表示由于患者死亡而導致的易感者減少速度, -a(u+v)u項表示感染者與易感者“交感”易感者變為患者后使易感者減少的速度, -bu2v2項表示采取一般防疫措施后使感染者減少的速度, -cu2v2項表示采取一般防疫措施后使易感者減少的速度,F(u,v)項表示由于其他相關因素的干擾使感染者增加的速度, -G(u,v)項表示采取特殊防疫措施后使易感者減少的速度, 不妨設F,G為充分光滑的有界函數. 系統(1)-(2)是一類在患區人群HIV傳播的生態動力學模型. 本文通過構造模型(1)-(2)的近似解, 利用得到的表示式考察HIV的傳播性態和規律.

先考慮系統(1)-(2)的一類相關問題:

由系統(3)-(4), 可得

其中C0和D0為任意常數, 可由系統的初始狀態確定.

2 泛函同倫映射

考慮HIV生態動力學非線性微分模型(1)-(2)的解. 顯然, 非線性微分系統一般不能用有限項的初等函數得到其精確解. 下面用泛函同倫映射方法求其近似解.

先引入如下一組泛函分析同倫映射[27]Hi(u,v,p)(i=1,2):2×I→:

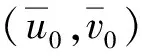
顯然, 由泛函分析同倫映射(7),(8)知,Hi(u,v,1)=0(i=1,2)與系統(1)-(2)相同. 故系統(1)-(2)的解(u(t),v(t))即為當p→1時,Hi(u,v,p)=0(i=1,2)的解.

設

(9)

將式(9)代入Hi(u,v,p)=0(i=1,2)中, 并比較方程Hi(u,v,p)=0(i=1,2)關于p同次冪的系數, 由p零次冪的系數得

(10)

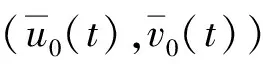
在Hi(u,v,p)=0(i=1,2)中, 取關于p1的系數, 得

由系統(13)-(14), 在零初值下可得

于是令p=1, 由式(9)可得系統(1)-(2)的一次近似解(u1app(t),v1app(t))為

將式(9)代入Hi(u,v,p)=0(i=1,2)中, 并取關于p2的系數為零, 得

其中:

由于系統(19)-(20)在零初值下, 故可得

于是令p=1, 由式(9)可得系統(1)-(2)的二次近似解(u2app(t),v2app(t))為

同理依次可得(ui(t),vi(t))(i=3,4,…). 再將(ui(t),vi(t))(i=0,1,2,…,n)代入式(9), 并令p=1, 依次可得系統(1)-(2)的各次解(unapp(t),vnapp(t))(n=3,4,…).

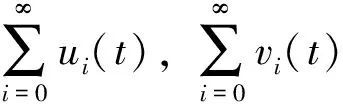
3 應用實例

為簡單, 設HIV傳播人群生態動力學微分系統(1)-(2)中的參數為無量綱數:a=b=c=e=h=1,F=G=0, 于是系統(1)-(2)為

利用泛函分析同倫映射方法, 由式(11),(12), 不妨取任意常數C0=D0=1, 則

由式(15),(16)得

由式(21),(22)得

于是由式(23),(24)和式(27)～(32), 可得系統(25)-(26)的二次近似解(u2app(t),v2app(t))為

感染者人數和易感者人數二次近似式(33),(34)的模擬曲線及相應的模擬精確解曲線分別如圖1和圖2所示. 繼續進行， 可依次得到HIV傳播人群的生態動力學微分系統模型(25)-(26)的更高次近似解.

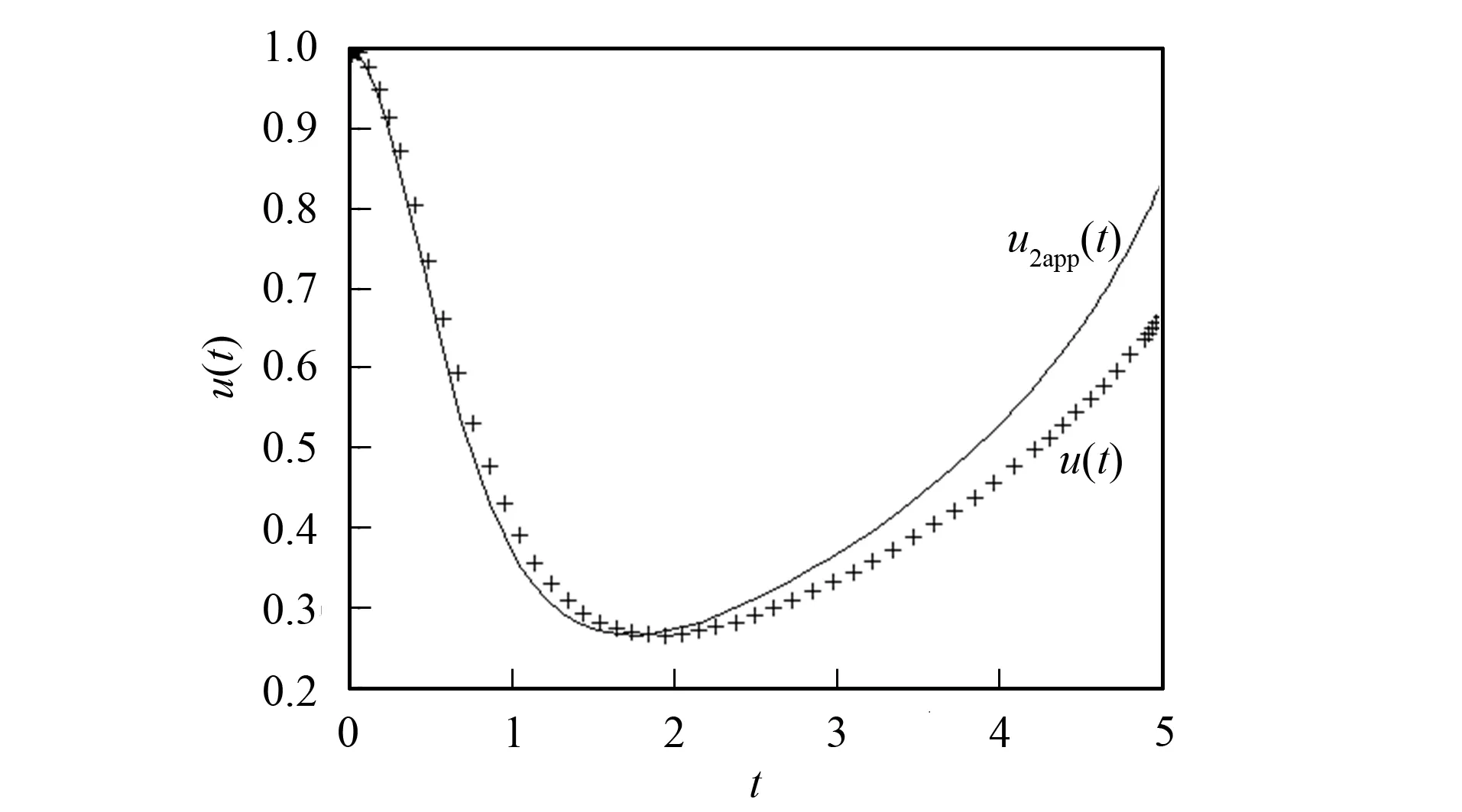
圖1 二次近似解u2app(t)與精確解u(t)的模擬曲線Fig.1 Simulation curves of second approximate solutions u2app(t) and exact solutions u(t)

圖2 二次近似解v2app(t)與精確解v(t)的模擬曲線Fig.2 Simulation curves of second approximate solutions v2app(t) and exact solutions v(t)

4 改變系統參數

改變無量剛系統模型近似解u2app(t),v2app(t)的相關參數, 可調節HIV傳播人群感染者人數和易感者人數的分布. 下面以系統(25)-(26)為例進行說明.

1) 改變參數a. 在無量剛系統(25)-(26)中, 僅改變參數a, 其他參數不變, 得到u2app(t)和v2app(t)的模擬曲線分別如圖3和圖4所示.

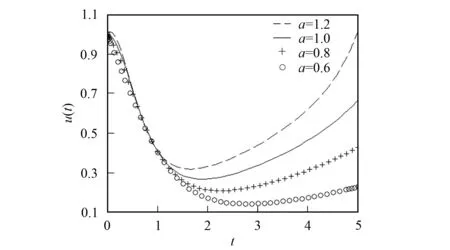
圖3 當a=1.2,1.0,0.8,0.6時, u2app(t)的模擬曲線Fig.3 Simulation curves of u2app(t) when a=1.2,1.0,0.8,0.6

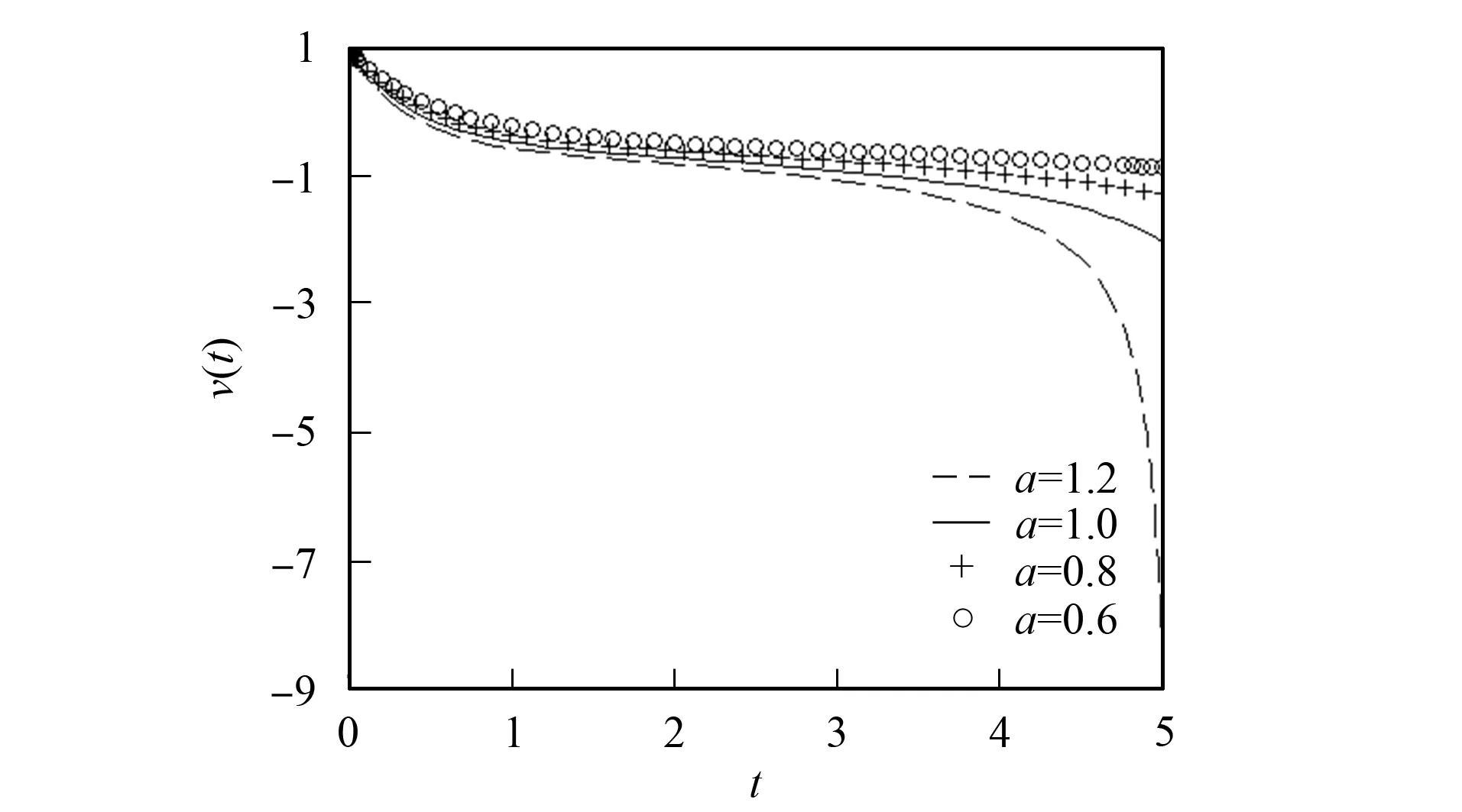
圖4 當a=1.2,1.0,0.8,0.6時, v2app(t)的模擬曲線Fig.4 Simulation curves of v2app(t) when a=1.2,1.0,0.8,0.6

2) 改變參數b,c. 在無量剛系統(25)-(26)中, 僅改變參數b,c, 其他參數不變, 得到u2app(t)和v2app(t)的模擬曲線分別如圖5和圖6所示.

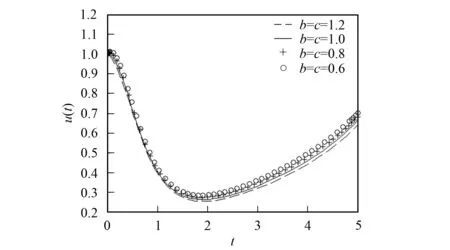
圖5 當b=c=1.2,1.0,0.8,0.6時, u2app(t)的模擬曲線Fig.5 Simulation curves of u2app(t) when b=c=1.2,1.0,0.8,0.6

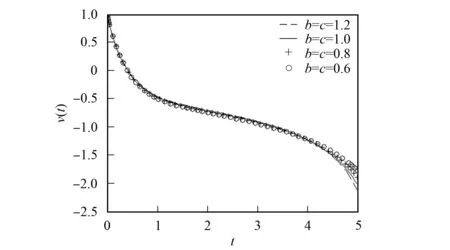
圖6 當b=c=1.2,1.0,0.8,0.6時, v2app(t)的模擬曲線Fig.6 Simulation curves of v2app(t) when b=c=1.2,1.0,0.8,0.6

3) 改變參數e,h. 在無量剛系統(25)-(26)中, 僅改變參數e,h, 其他參數不變, 得到u2app(t)和v2app(t)的模擬曲線分別如圖7和圖8所示.

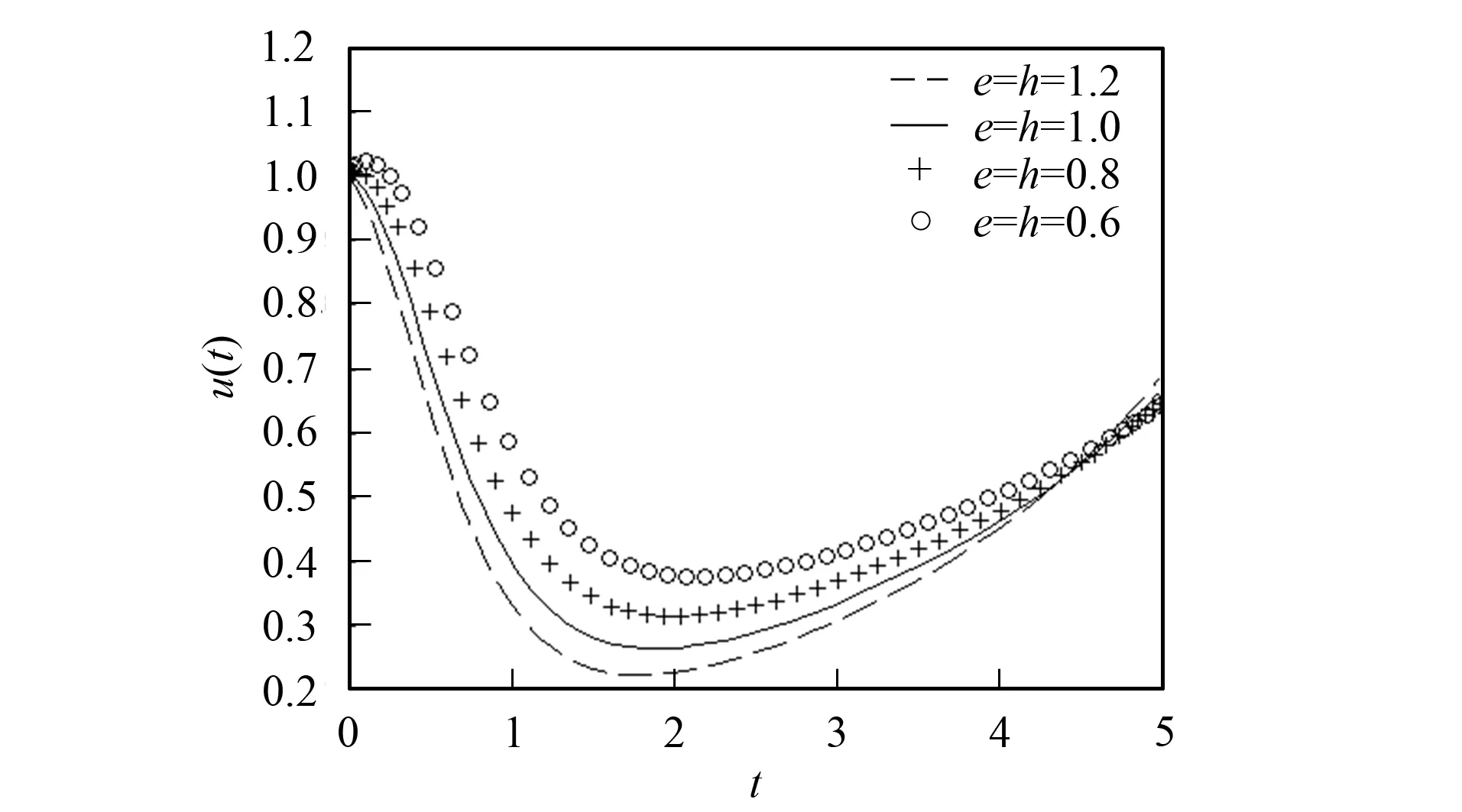
圖7 當e=h=1.2,1.0,0.8,0.6時, u2app(t)的模擬曲線Fig.7 Simulation curves of u2app(t) when e=h=1.2,1.0,0.8,0.6

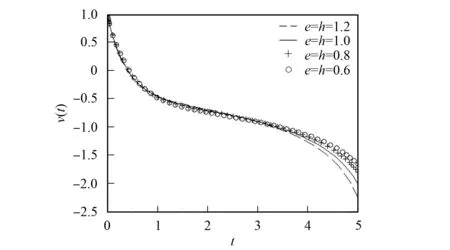
圖8 當e=h=1.2,1.0,0.8,0.6時, v2app(t)的模擬曲線Fig.8 Simulation curves of v2app(t) when e=h=1.2,1.0,0.8,0.6

由圖3～圖8可見, 改變系統(25)-(26)的參數, 可改變感染者人數和易感者人數的分布. 因此, 可利用近似解的表示式調節感染者人數和易感者人數的分布, 達到在各時間段內控制相關人數的目的.