一類分數階橢圓型方程的非平凡解

張 申 貴

(西北民族大學 數學與計算機科學學院, 蘭州 730030)

0 引 言

考慮如下分數階橢圓型方程:

(1)

其中:Ω是N中具有局部Lipschitz邊界?Ω的有界開集,N>ps,s∈(0,1),p∈(1,+∞); 參數λ≥0;F(x,u)=f(x,s)ds. 設A(t): [0,+∞)→+和B(t):→為連續函數.

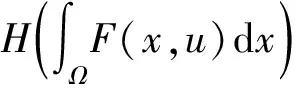
分數階微分方程在控制論、電化學和神經元等領域應用廣泛. 目前, 關于分數階橢圓型方程的研究已有很多結果, 如: 文獻[3]討論了分數階Sobolev空間的性質; 文獻[4]研究了一類帶有臨界指數的分數階Kirchhoff型方程的可解性; 當非線性項帶有參數時, 文獻[5]討論了分數階Laplace方程非平凡解的存在性和分歧問題; 文獻[6]研究了分數階Laplace方程在自由邊界上的變分問題; 當p=2,A(t)=B(t)=1時, 文獻[7-8]利用山路定理研究了問題(1)多重解的存在性; 文獻[9]利用Morse理論和計算臨界群的方法, 得到了分數階p-Laplace方程

非平凡解的存在性, 其中方程右端的非線性項f(x,u)滿足(AR)型超線性條件: 即存在μ>p,L>0, 使得

0<μF(x,u)≤f(x,u)u

其中函數K:N{0}→(0,+∞)滿足:

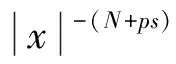
?t∈.

本文在一類不同于(AR)條件的超線性條件下, 利用文獻[13]中建立的臨界點定理研究問題(1)非平凡解存在的充分條件.

1 預備知識

定義1[9]分數次Sobolev空間Ws,p(N)定義為

其中S表示可測實值函數組成的集合. 記

X(Ω)={u∈Ws,p(N)|u(x)=0, a.e.x∈NΩ},

X(Ω)上的范數為

引理2[9]記

?u,v∈X(Ω).

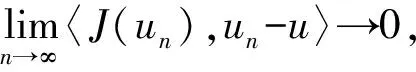
引理3(臨界點定理)[13]設X為Banach空間, 泛函Iλ∈C1(X,), 且下列條件成立:

2) 泛函Iλ下方無界;

3) 記泛函Iλ∶=Φ-λΨ, 且Φ,Ψ∈C1(X,)滿足Φ下方有界,Φ(0)=Ψ(0)=0. 給定r>0, 對每個有則對于泛函Iλ至少有兩個非平凡的臨界點.

若對?v∈X(Ω), 有

則稱u∈X(Ω)為問題(1)的弱解.

在X(Ω)上定義能量泛函Iλ如下:

其中:

則Iλ(u)∈C1(X(Ω),), 且

從而u∈X(Ω)是問題(1)的(弱)解等價于u是泛函Iλ的臨界點.

2 主要結果

假設下列條件成立:

(H1) 設存在常數a0>0, 使得對所有的t∈[0,+∞)，A(t)≥a0均成立；

(H2) 設存在常數η≥1, 使得對所有的t∈[0,+∞)，

均成立；

(H3) 設存在常數b0>0,b1>0, 使得對所有的t∈,b0≤B(t)≤b1均成立;

(H6) 設存在常數L>0,c1>0,c2>0, 使得:

1) 當|u|≥L時, 有

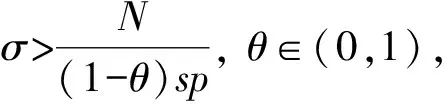
本文主要結果如下:

定理1設條件(H1)～(H7)成立, 則存在λ*>0, 使得對每個λ∈[0,λ*], 問題(1)均至少有兩個非平凡解.

證明: 1) 證明泛函Iλ滿足(C)條件. 設{un}?X(Ω)為泛函Iλ的(C)序列, 則

(un)‖≤c3, |Iλ(un)|≤c3.

(2)

首先, 證明序列{un}在X(Ω)中有界. 假設{un}在X(Ω)中無界, 則當n→∞時,

‖un‖→+∞.

(3)

且

(4)

由假設條件(H2)～(H4)和式(3), 有

由假設條件(H5)及(H6)中1)知, 存在常數c5>0, 使得對所有的x∈Ω和u∈,

(7)

均成立. 結合式(6),(7), 有

(8)

(9)

結合式(5),(9), 當n→∞時, 有

(10)

當n充分大時, 由條件(H6)中2)及式(6), 有

(11)

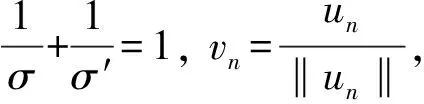
由假設條件(H1),(H3), 有

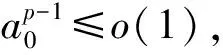
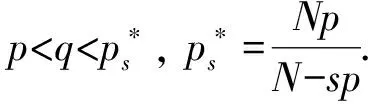
記

?u,v∈X(Ω).

2) 證明泛函Iλ滿足引理3中條件2). 令

由假設條件(H2), 有

(14)

利用假設條件(H4)同理可證, 存在c9>0,c10>0, 使得對?t∈時, 有

(15)

由假設條件(H7), 對于?υ>0, 存在c11>0, 使得

(16)

對所有的x∈Ω和u∈成立. 取u0∈X(Ω){0}, 對于t>1, 由式(14)～(16)及λ≥0, 有

令υ充分大, 使得

3) 證明泛函Iλ滿足引理3中條件3). 記

Iλ(u)∶=Φ-λΨ∈C1(X(Ω),),

其中:

由條件(H1), 有

(18)

式(18)表明, 泛函Φ下方有界, 且對于u∈X(Ω), 滿足Φ(u)<1, 有

‖u‖

(19)

(20)

(21)

結合假設條件(H3),(H5)及式(19)～(20), 對于u∈X(Ω), 且滿足Φ(u)<1, 有

注1令非局部系數A(t)=a+bpt, 其中:t≥0;p∈(1,+∞);a和b為正常數. 則函數A(t)滿足條件(H1)和(H2).

事實上,A(t)=a+bpt≥a>0, 易見a0=a. 取η=p, 對t≥0, 有

令B(t)=arctant+π, 則有

從而B(t)滿足條件(H3),(H4). 取A(t)=B(t)=1, 此時η=1, 令p=2, 且

則F滿足定理1中條件, 但不滿足(AR)條件, 也不滿足文獻[2-12]中定理的條件.