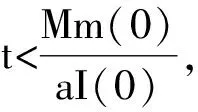一維可壓縮量子Navier-Stokes方程組解的爆破
董建偉, 朱軍輝, 薛紅霞
(鄭州航空工業(yè)管理學(xué)院 理學(xué)院, 鄭州 450015)
1 引言與主要結(jié)果
考慮如下一維可壓縮量子Navier-Stokes方程組[1]:
其中: 粒子密度ρ與粒子速度u為未知函數(shù); Planck常數(shù)ε>0與黏性常數(shù)ν>0為物理參數(shù); 函數(shù)P(ρ)=ργ(γ≥1)表示壓力. 該類模型可用于描述超流體[2]、量子半導(dǎo)體[3]、弱相互作用的玻色氣體[4]和波曼力學(xué)的量子軌跡等[5]. Brull等[6]利用動量方法和Champan-Enskog展開法由Wigner方程得到了可壓縮量子Navier-Stokes方程組; Jüngel等[7-8]用不同方法得到了完整的量子Navier-Stokes方程組(包含能量方程). 可壓縮量子Navier-Stokes方程組是可壓縮Navier-Stokes方程組的重要逼近方程組, 可用于證明三維黏性退化可壓縮Navier-Stokes方程組弱解的整體存在性[9-10]. 此外, 可壓縮量子Navier-Stokes方程組也是不可壓縮Navier-Stokes方程組[11-13]和不可壓縮Euler方程組[14]的逼近方程組.
在周期邊界條件下, Jüngel[15]首先證明了當(dāng)Plank常數(shù)大于黏性常數(shù)(ε>ν)時, 多維可壓縮量子Navier-Stokes方程組弱解的整體存在性; Dong[16]和Jiang[17]分別將文獻(xiàn)[15]的結(jié)果推廣到ε=ν和ε<ν的情形. 但在文獻(xiàn)[15-17]的整體弱解定義中, 動量方程的試驗函數(shù)是ρφ, 而不是φ, 導(dǎo)致在三維空間中要求條件γ>3, 使得其在物理意義上受到限制. 通過在動量方程(2)中引入額外的冷壓力[18]或添加阻尼項[10], 可改進(jìn)動量方程的試驗函數(shù)及條件限制γ>3.
目前, 關(guān)于模型(1)-(2)光滑解整體存在性的研究文獻(xiàn)報道較少. 文獻(xiàn)[19]在初始密度為正且ε=ν的條件下, 得到了模型(1)-(2)一維模型光滑解的整體存在性; 文獻(xiàn)[1]在一維有界區(qū)域中得到了當(dāng)ε≥ν時一個解的爆破結(jié)果, 即其解將在有限時刻失去其正則性. 本文在去掉條件ε≥ν的情形下, 得到另一個解的爆破結(jié)果. 考慮一維量子Navier-Stokes方程組的如下初邊值問題:
與文獻(xiàn)[1]不同, 本文通過假設(shè)與初始動量有關(guān)的泛函充分大, 得到解的爆破結(jié)果. 為此定義:
其中: m(t)表示區(qū)域(0,1)中的粒子總質(zhì)量; E(t)表示總能量泛函, 包括動能、熱力學(xué)焓(若γ>1, 則H(ρ)=ργ/(γ-1), 若γ=1, 則H(ρ)=ρ(lnρ-1)+1和量子能; I(t)表示加權(quán)動量; 權(quán)函數(shù)f(x)滿足下列條件:
(H1) f(x)∈C2[0,1], f(0)=0, 且f′(x)>0, x∈[0,1]. 記
本文主要結(jié)果如下:
定理1設(shè)ρ∈H1(0,T;L2(0,1))∩L2(0,T;H3(0,1)), 在[0,1]×[0,T]上ρ>0, u∈H1(0,T;L2(0,1))∩L2(0,T;H2(0,1)), (ρ,u)是問題(3)-(8)的解, 其中初始條件滿足
0<ρ0(x)∈H1(0,1),u0(x)∈L2(0,1),I(0)>0,
且權(quán)函數(shù)f(x)滿足條件(H1). 若
(15)
其中a∈(0,1)是任意固定的常數(shù), 則其解的存在時間T滿足
(16)
注1如文獻(xiàn)[1]中注1.1所述, 雖然關(guān)于定理1正則性解的局部存在性研究目前尚未見文獻(xiàn)報道, 但由量子Navier-Stokes方程組與黏性量子Euler方程組的等價性[15], 可利用文獻(xiàn)[20-21]中方法和技巧證明其解的局部存在性, 本文只關(guān)注其解的爆破.
注2邊界條件(7)表示在右邊界處量子效應(yīng)消失, 邊界條件(8)是為了使邊界積分為零而提出的技術(shù)性條件.

2 定理1的證明
引理1在定理1的條件下, 對任意t∈[0,T], 成立m(t)=m(0), E(t)≤E(0).
證明: 由式(3)和式(8), 有
(17)
所以對任意t∈[0,T], 有m(t)=m(0). 將式(4)兩邊同乘以u, 再在(0,1)上積分, 得
利用邊界條件(6),(8), 并注意到P′(ρ)=ρH″(ρ), 有
(20)
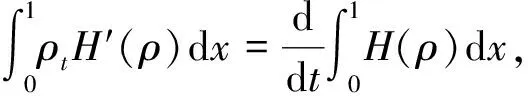
(21)

(22)

(23)
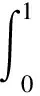
(24)

(25)

(26)
由式(20)~(26)知, 式(18)與式(19)之和為
(27)
所以對任意t∈[0,T], 有E(t)≤E(0).
引理2在定理1的條件下, 對任意t∈[0,T], 成立
(28)
證明: 將式(4)兩邊同乘以函數(shù)f(x), 再在(0,1)上積分, 得
其中用到了P(ρ)=ργ, γ≥1. 下面逐項估計式(29)的右端.
由Cauchy不等式, 得
(30)
由式(30),(12),(9)和引理1可得
(31)
利用分部積分、條件(H1)和式(6), 可得
(32)
利用分部積分、式(6)~(8)、條件(H1)和Cauchy不等式, 可得式(29)右端最后兩項的估計為
由式(29),(31)~(34),(13)~(14),(9)~(10)和引理1, 可得
下面證明定理1. 由式(28), 有
(35)
其中a∈(0,1)是任意固定的常數(shù). 由式(35)和條件(15)知, 當(dāng)t較小時有I(t)>I(0), 由I(0)>0知, 當(dāng)t較小時有I(t)>0, 再由式(35)和條件(15)知, I(t)>0在[0,T]上是遞增函數(shù), 且下列不等式成立:
(36)
固定t∈(0,T), 將式(36)兩邊同除以I2(t), 再在(0,t)上積分, 得