奇異隨機(jī)微分方程的依分布幾乎自守解

常 晶, 趙 昕, 蔣慧杰

(吉林農(nóng)業(yè)大學(xué) 信息技術(shù)學(xué)院, 長春 130118)

隨機(jī)微分方程的幾乎自守解在力學(xué)、物理、統(tǒng)計(jì)學(xué)和生物數(shù)學(xué)等領(lǐng)域應(yīng)用廣泛. 幾乎自守函數(shù)是幾乎周期函數(shù)的推廣, 由于幾乎自守現(xiàn)象在符號(hào)動(dòng)力系統(tǒng)中表現(xiàn)出某種復(fù)雜性和混沌現(xiàn)象, 因此得到廣泛關(guān)注. 付苗苗等[1]首先引入了幾乎自守過程, 此后關(guān)于隨機(jī)微分方程幾乎自守解的研究得到深入發(fā)展[2-3]. 但關(guān)于依分布幾乎自守解的研究目前文獻(xiàn)報(bào)道較少, 文獻(xiàn)[4-6]得到了隨機(jī)微分方程的依分布幾乎自守解; 陳鋒等[7]得到了依狀態(tài)切換的隨機(jī)微分方程的幾乎自守解. 奇異線性系統(tǒng)在網(wǎng)絡(luò)理論等領(lǐng)域應(yīng)用廣泛[8-9]. Diagana等[10]研究了奇異隨機(jī)微分方程均方意義下的幾乎周期解. 本文利用文獻(xiàn)[10-11]中塊對(duì)角化的技巧, 考慮奇異隨機(jī)微分方程依分布意義下的幾乎自守解.

1 預(yù)備知識(shí)

設(shè)(H,‖·‖) 是可分的Hilbert空間,W(t)為定義在概率空間(Ω,F,P,(Ft)t≥0)上的布朗運(yùn)動(dòng), 其中Ft=σ(W(u)-W(v)|u,v≤t),L2(Ω,H )為所有H值隨機(jī)變量x組成的空間, 且

設(shè)(U,‖·‖U)為可分的Hilbert空間,L(U,H )是從U到H的所有有界線性算子空間.

定義1[7]對(duì)于隨機(jī)過程x(t):→L2(P,H ), 如果對(duì)所有的s∈, 有

定義2[7]對(duì)于L2-連續(xù)隨機(jī)過程x(t):→L2(P,H ), 如果對(duì)于序列?, 存在一個(gè)子列sn?和一個(gè)隨機(jī)過程y(t):→L2(P,H ), 使得

對(duì)所有的t∈都成立, 則稱x(t)是二階矩意義下幾乎自守的.

定義3[7]對(duì)于一個(gè)連續(xù)隨機(jī)過程x, 如果t→μt∶=μ(x(t)):→Pr(C(,X))是幾乎自守的, 則稱x為依分布幾乎自守的, 其中μ(x(t))∶=P°[x(t)]-1為P下分布的.

則稱x(t)是依分布幾乎自守的.

2 主要結(jié)果

考慮奇異隨機(jī)微分方程

Adx(t)+Bx(t)dt=f(t)dt+g(t)dW(t),t∈

(1)

依分布的幾乎自守解, 其中：A:D(A)?H→H,B:D(B)?H→H是閉的線性算子, 且D(B)?D(A);f:→L2(Ω,H ),g:→L(U,H )為幾乎自守隨機(jī)過程;W(t)是U-值布朗運(yùn)動(dòng).B(H )表示所有有界線性算子H的集合,D(S),ρ(S),N(S)和R(S)分別表示線性算子S的定義域、豫解式、值域和像集, 且R(λ,S)∶=(λI-S)-1, 其中:λ∈ρ(S);I: H→H為H的單位算子. 假設(shè)f,g為幾乎自守的隨機(jī)過程, 且線性算子B有一個(gè)有界逆. 因?yàn)锽有連續(xù)逆, 且D(B)?D(A), 定義T=AB-1: H→H為連續(xù)線性算子, 則R(λ,T)=(λI-T)-1:ρ(T)→B(H ). 利用文獻(xiàn)[8-9], 令Bx=y,x∈D(B)?D(A), 則方程(1)可化為

Tdy(t)+y(t)dt=f(t)dt+g(t)dW(t),t∈.

(2)

且H =R(T)⊕N(T)=X1+X2. 顯然, 由R(λ,T)定義知,T為限制在X1=R(T)上的有界逆算子, 則T可寫為

其中M為限制在X1上的有界線性算子.T也可視為X1上的C0半群. 利用T的對(duì)角塊形式及f,g兩個(gè)隨機(jī)過程分別在X1和X2上的投影分解:

方程(2)可分解為

M-1dy1(t)+y1(t)dt=f1dt+g1(t)dW(t),y2(t)=f2(t)+g2(t).

(3)

則y=(y1,y2)有如下形式:

(4)

其中t,τ∈且t≥τ. 則式(3),(4)可等價(jià)地寫成如下等式:

(5)

其中t,τ∈且t≥τ.

假設(shè)原點(diǎn)的C0-半群T(t)=(e-Mt)t≥0是指數(shù)穩(wěn)定的, 即存在常數(shù)K≥1和ω>0, 使得

‖T(t)‖X1≤Ke-ωt,t≥0.

定理1如果f,g為幾乎自守的, 則方程(1)存在唯一依分布的幾乎自守解.

證明: 首先y為方程(1)的有界溫和解, 下面證明y是方程(3)的唯一幾乎自守解. 要證y2是幾乎自守過程, 只需證y1滿足方程(4)也是幾乎自守過程.y1可化為

即

對(duì)所有的t∈均成立. 利用Cauchy-Schwarz不等式, 可得

其中F為幾乎自守函數(shù). 類似地, 因?yàn)間1也是幾乎自守的, 則對(duì)于>0, 有

因?yàn)?/p>

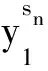
下面證明解的唯一性. 令

為方程(1)在分布意義下的兩個(gè)幾乎周期解, 再令w1=u1-v1, 可得w1=e-M(t-s)w1(s). 當(dāng)t≥s時(shí),w1有界, 則對(duì)所有的t≥s, 有

令(τn)n∈, 當(dāng)n→∞時(shí),τn→-∞, 對(duì)于任意固定的t∈, 存在子序列(τnk)k∈, 使得對(duì)于所有的k∈, 有τnk