一種改進的LSTSVM增量學習算法

周水生, 姚 丹

(西安電子科技大學 數學與統計學院, 西安 710126)

支持向量機(support vector machines, SVM)[1]的主要思想是最大限度地分開兩類訓練樣本. 由于SVM能較好地克服維數災難等問題, 因而在模式分類、回歸分析、文本分類和生物信息學等領域應用廣泛[2-4]. 為了研究交叉分類問題, Jayadeva等[5]提出了非平行平面的分類器, 即孿生支持向量機(twin support vector machines, TWSVM), 其基本思想是構造兩個非平行的超平面進行分類, 其中每個超平面擬合一類樣本且盡量遠離另一類樣本. TWSVM將傳統的一個規模較大的凸二次規劃問題轉化為兩個規模較小的凸二次規劃問題, 提高了訓練速度[6]. 邵元海等[7]在TWSVM的基礎上提出了孿生邊界支持向量機(twin bound support vector machines, TBSVM), 其通過在目標函數上增加正則化項實現結構風險最小化. 目前, 對TWSVM的改進已有許多[8-9], 使得TWSVM在魯棒性和泛化性能等方面均有提高. Kumar等[10]提出了最小二乘孿生支持向量機(least squares twin support vector machines, LSTSVM), 與LSSVM的不同點在于求解過程變成了求解兩個等式方程組, 因而提高了求解效率, 減少了存儲空間. 基于LSTSVM, 陳靜等[11]提出了加權的最小二乘孿生支持向量機(weighted least squares twin support vector machines, WLSTSVM), 其通過對樣本增加權重, 提高該算法的魯棒性, 但WLSTSVM分類效果的好壞取決于權重的選擇, 從而制約了其應用范圍.

當樣本數據規模較大時, 文獻[10,12-13]給出的LSTSVM算法需要訓練樣本較多, 使模型出現求逆過程計算量大、易產生過擬合、訓練速度慢、計算復雜度高等缺點. 針對LSTSVM算法的不足, 本文基于Sherman-Morrison定理[14]和迭代算法提出一種改進的最小二乘孿生支持向量機(based on Sherman-Morrison theorem and iterative algorithm an improved least squares twin support vector machine, SMI-ILSTSVM)增量學習算法, 對最小二乘孿生支持向量機進行改進和優化.

1 最小二乘孿生支持向量機

LSTSVM的基本思想是通過構造兩個超平面進行分類, 每個超平面回歸一類樣本且盡量遠離另一類樣本[5]. 線性的LSTSVM就是求解下述問題：

LSTSVM1：

(1)

LSTSVM2：

(2)

其中: A表示正類樣本; B表示負類樣本;c1,c2表示懲罰參數; e1和e2表示全一向量. 根據式(1),(2), 可求得線性LSTSVM的解為

(3)

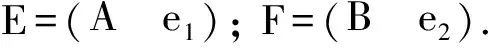
(4)

最后, 可使用所得到的超平面(4), 并應用判別函數, 即

(5)

非線性情況通過構造核函數的方法獲得, 非線性的LSTSVM為

(6)

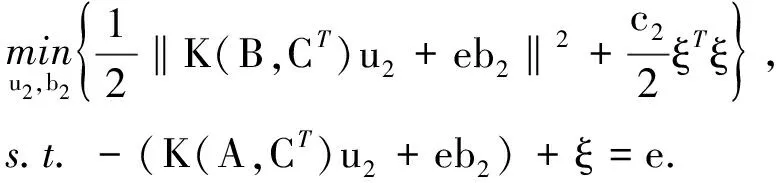
(7)

根據式(6),(7), 可求得非線性LSTSVM的解為

(8)

(9)

(10)

2 改進的最小二乘孿生支持向量機

由于LSTSVM的求解難度在于求解規模為(m+1)×(m+1)矩陣的逆, 如果該矩陣為非滿秩矩陣, 則求解結果會出現病態解的現象[6]. 文獻[13,15]都是基于經驗風險最小化原則對LSTSVM進行不同的改進, 所以本文提出一種改進的最小二乘孿生支持向量機(improved least squares twin support vector machine, ILSTSVM).

2.1 線性ILSTSVM

在線性LSTSVM的目標問題上加入經驗風險最小化原則, 得到下述問題：

ILSTSVM1：

(11)

ILSTSVM2：

(12)

可以求出式(11),(12)的解, 即

(13)

2.2 非線性ILSTSVM

對于非線性的情況, 采用核函數的方法, 即

類似于線性ILSTSVM的求解方法, 可求出式(14),(15)的解, 即

(16)

3 SMI-ILSTSVM增量學習算法

3.1 矩陣求逆分解定理

本文提出的SMI-ILSTSVM算法, 主要采用對矩陣的逆進行分解, 然后重組矩陣的逆, 最終得到一種結構相對簡單、計算量較小的迭代求解算法, 其原理是通過迭代求解利用前一次的計算結果求逆, 不必直接求大樣本矩陣的逆.

定理1(Sherman-Morrison定理)[14]若矩陣A是一個可逆矩陣, u和v均為向量, 且

1+vTA-1u≠0,

則當u=v時,

(17)

3.2 線性SMI-ILSTSVM增量學習算法

增量學習(incremental learning)[16]算法降低了對時間和空間的需求, 更能滿足實際要求, 但每次迭代過程中只增加一個樣本, 會導致計算效率偏低. 本文采用隨機法選擇訓練樣本, 在一定程度上降低了增量學習算法對分類精度的影響, 且每次隨機選擇一列訓練樣本也提高了計算效率.

(18)

所以對于擴展矩陣E計算更新后的ETE, 僅添加了一個小矩陣ssT, 更新后SMI-ILSTSVM模型的解可寫為

(19)

由于式(19)中存在單位矩陣, 所以式(19)總是非奇異的, 此時可利用式(17)分解矩陣的逆. 令

(20)

則v1=-M-1FTe2, v2=N-1ETe1. 進一步計算可得

根據上述推導過程, 線性SMI-ILSTSVM增量學習算法如下.

算法1線性SMI-ILSTSVM增量學習算法.

輸入: 訓練集{X,L}, 罰參數ci>0(i=1,2,3,4);

1) (n,m)=size(X);

3) fori=1∶ndo

s=(Si)T和l=Li;

4) ifi==1 then

5) else

7) end if

8) end for.

觀察線性ILSTSVM的解式(13), 可知該模型的復雜度為O(((m+1)3+(m+1)2)n), 而線性SMI-ILSTSVM增量學習算法的復雜度為O(2(m+1)2n), 降低了復雜度, 因此, SMI-ILSTSVM增量學習算法計算效率更高.

3.3 非線性SMI-ILSTSVM增量學習算法

非線性SMI-ILSTSVM的擴展向量為

由于非線性情形下計算高斯核矩陣需花費大量的時間和內存, 因此可先隨機選取樣本C的子集Z, 用核矩陣K(A,ZT)代替K(A,CT), 使SMI-ILSTSVM算法在訓練時僅使用部分樣本數據, 不但減少了算法的總計算量, 且降低了存儲空間, 在不影響分類性能的基礎上, 使算法具有稀疏性.

衡量稀疏性的一個指標----稀疏水平[17]的計算公式為

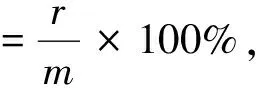
(22)

其中:r為訓練樣本中非零解數量的比例;m為訓練樣本的大小. 先令

(23)

則

v1=-P-1HTe2, v2=Q-1GTe1.

進一步計算可得

其中:

根據上述推導過程, 非線性SMI-ILSTSVM增量學習算法如下.

算法2非線性SMI-ILSTSVM增量學習算法.

輸入: 訓練集{X,L}, 罰參數ci>0(i=1,2,3,4), 高斯核函數參數σ∈(2-11,23);

1) (n,m)=size(X);

3) fori=1∶ndo

4) ifi==1 then

5) else

7) end if

8) end for.

4 實驗結果與分析

為了評價SMI-ILSTSVM算法的性能, 下面進行人工數據和UCI數據集的仿真實驗. 實驗條件為： Windows7系統, 8 GB內存, Intel(R)Core(TM)i7-4790 CPU@3.6 GHz, MATLAB R2014a, 核函數為

4.1 人工生成數據實驗

先隨機生成200個交叉型樣本點, 其中左類和右類各100個, 分別用SVM和TWSVM構造分類面. 實驗結果表明, TWSVM的精度約為90%, 而線性SVM的精度約為60%. 對于交叉型數據集, TWSVM的分類效果比SVM的分類效果好. LSTSVM,WLSTSVM和SMI-ILSTSVM三種分類器針對含有噪聲的交叉樣本集的分類結果如圖1所示.

圖1 3種分類器的分類結果Fig.1 Classification results of three classifiers

由圖1可見, LSTSVM和WLSTSVM分類器在交叉樣本點上受噪聲影響較大, 這是因為文獻[11]提出的權重算法對于交叉數據集缺乏魯棒性, 而本文提出的SMI-ILSTSVM增量學習算法的分類效果較好.

4.2 UCI數據集的實驗結果

為了驗證SMI-ILSTSVM增量學習算法的分類性能, 本文選取列于表1中的6個標準UCI數據集, 并分別對線性和非線性兩種類型的SMI-ILSTSVM,WLSTSVM,LSTSVM,TWSVM進行分類精度與訓練時間的仿真實驗. 在實驗中, 線性情形采用線性核函數, 非線性情形采用高斯核函數, 訓練集隨機選取原有訓練集的30%進行訓練, 核參數在區間[2-11,23]內選取, 懲罰參數ci>0(i=1,2,3,4)在區間[0,2]內選取, 所有參數的選取方法均采用十折交叉驗證法[7,10]. 4種方法得到的分類結果列于表2～表5.

表1 標準UCI數據集屬性

表1可見, 本文提出的線性SMI-ILSTSVM增量學習算法對于6種UCI數據集的分類精度和訓練時間均好于TWSVM,LSTSVM和WLSTSVM. 對于同一個數據集, SMI-ILSTSVM的分類精度基本上最高, WLSTSVM的分類精度次之, 而TWSVM和LSTSVM的分類精度差別不大； SMI-ILSTSVM的訓練時間最少, TWSVM的訓練時間最多.

表2 線性核情形下4種方法的分類精度比較

表3 線性核情形下4種方法的訓練時間比較

表4 非線性核情形下4種方法的分類精度比較

表5 非線性核情形下4種方法的訓練時間比較

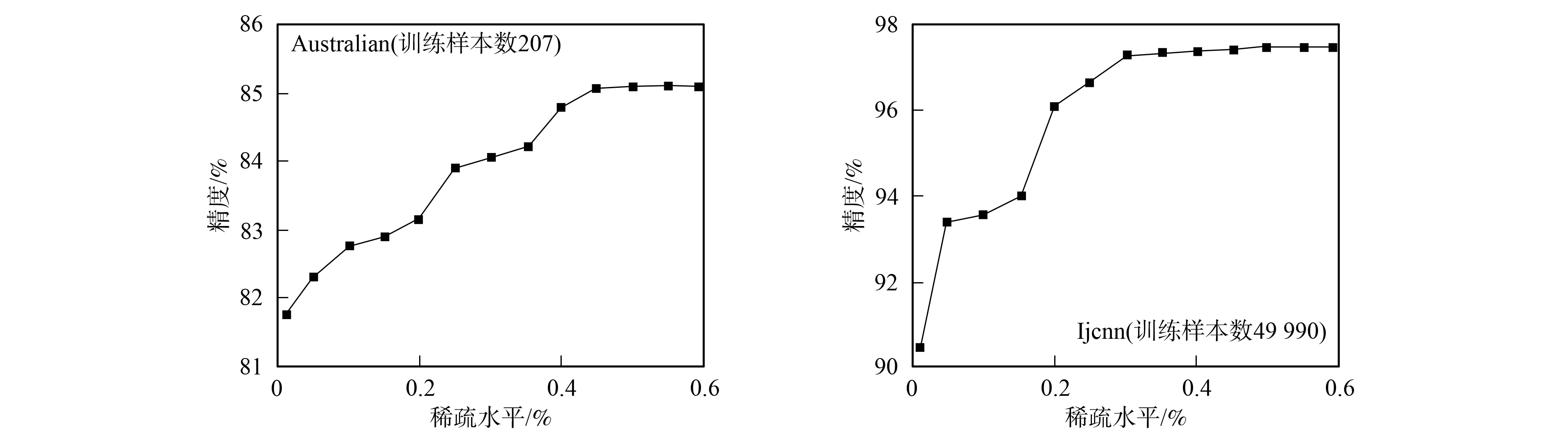
圖2 大規模數據集的稀疏水平Fig.2 Sparse level of large scale datasets

由表2～表5可見, 本文提出的非線性SMI-ILSTSVM增量學習算法對于6種UCI數據集的分類精度和訓練時間均好于TWSVM,LSTSVM和WLSTSVM. 對于同一個數據集, SMI-ILSTSVM的訓練時間最少, 這是由于隨機選取訓練樣本的子集進行訓練, 可確保較少的訓練時間, 但犧牲了一定的分類精度； WLSTSVM的訓練時間最多, 是由于計算樣本權重提高分類精度比較耗時, 所以其分類精度較高. 因為非線性SMI-ILSTSVM增量學習算法在訓練時僅使用部分樣本數據, 所以在UCI數據集上并非一致地優于其他3種已有算法, 這也是本文算法有待進一步提高之處. 本文算法的優勢在于不僅降低了存儲空間, 而且減少了算法的總計算量, 使算法具有稀疏性. 稀疏性是解向量的非零元素個數, 本文使用其相對值, 即稀疏水平. 利用式(22)計算出不同訓練樣本對應的稀疏水平如圖2所示. 由圖2可見, 本文提出的非線性SMI-ILSTSVM增量學習算法對于大規模數據集均具有一定的稀疏水平.

綜上可見, 本文提出的SMI-ILSTSVM增量學習算法較LSTSVM算法具有更好的泛化性能, 避免了在求解該目標函數時對病態矩陣求逆的處理, 算法的分類精度和訓練時間有明顯提高； 采用隨機選擇法選取訓練樣本的一列, 在一定程度上降低了增量學習算法對分類精度的影響, 也提高了計算效率； 引入隨機選擇訓練樣本的一個子集代替全部訓練樣本, 使核函數的計算量減小, 從而使算法具有稀疏性, 減少了運算時間. 在UCI數據集上的實驗表明, 本文算法能實現高精度和高效率的分類效果, 且適用于含有噪聲的交叉樣本集分類.