基于離群因子的不確定數據生成算法

劉 鋼, 唐東凱, 王紅梅, 胡 明

(1. 長春工業大學 計算機科學與工程學院, 長春 130012； 2. 長春工程學院 計算機技術與工程學院, 長春 130012)

在對不確定數據進行分析、融合與挖掘前, 首先要獲得不確定數據. 目前, 現有的不確定數據主要從兩方面生成不確定數據集： 1) 從模擬數據集出發, 由于沒有真實數據集, 所以先人工產生確定的模擬數據集, 再采用相應的轉化策略生成不確定數據； 2) 從真實數據集出發, 如UCI機器學習數據集, 根據生成算法得到不確定數據集. 對于第一種方式, Chau等[1]首先在100×100的二維空間中隨機生成一系列點, 然后對每個點選擇一個不確定模型產生不確定性數據; 文獻[2-4]在此基礎上增加了一個大小隨機且位置固定的矩形MBR(minimum bounding rectangle), 然后將不確定對象均勻分布在MBR內, 并將MBR內的每個樣本點隨機產生一個概率值, 使概率值之和為1. 對于第二種方式, 金萍等[5]先在UCI數據集Glass,Iris,Wine的每一維上設置一個擾動區間, 然后使用擾動因子β(0<β<1)控制每個數據對象對應的MBR大小; 文獻[6-7]在確定數據集上添加了一個不確定數據生成策略, 為每個數據源中的樣本數據定義了一個概率密度函數fi, 使每個樣本對象由一組樣本點表示, 每個樣本點都對應一個概率值, 且概率之和為1; 文獻[8-10]使用不同的分布函數作為概率密度函數生成不確定數據.

目前不確定數據集的生成方法主要存在兩方面的不足： 1) 幾乎所有的不確定數據生成算法都未考慮原始數據集的數據分布特征, 如數據集中存在離群點, 離群點的存在會影響最后的挖掘結果； 2) 在上述生成方法中, 存在擾動因子β(0<β<1), 且其值在整個算法過程中固定不變, 不能很好地反映數據的分布特征. 為了解決目前不確定數據集生成方法存在的不足, 本文通過分析不確定數據的模型, 針對屬性級不確定數據, 先通過引入局部離群點檢測算法計算每個對象的離群因子, 然后使用離群因子的值產生擾動因子, 自動控制MBR的大小, 提出了AC-UDGen(attribute level continuous uncertain data set generation algorithm)算法. 實驗結果表明, AC-UDGen算法生成的不確定數據集在聚類時具有更好的聚類效果.

1 不確定數據模型

不確定數據模型的表示方式有多種, 較常見的是概率分布模型[11-12]. 概率分布模型由一個[0,1]間的概率值及確定的元組屬性值表示. 在實際應用中, 將不確定性數據分為存在級不確定性(也稱元組不確定性)和屬性級不確定性(也稱值不確定性)兩種.

1) 存在級不確定性. 一個事件在每次測試中是否發生都以一定的可能性存在, 而這個可能性的大小即為對應該事件發生的概率, 存在級不確定性是指一個數據對象存在與否用一個概率值的大小表示. 例如, 數據庫中有兩個不確定對象A和B, 其中A存在的概率為65%, 而B存在的概率為70%.A和B之間可能是相互獨立也可能存在依賴關系.

2) 屬性級不確定性. 數據對象是確定存在的, 但其屬性值具有不確定性. 一般采用概率值或概率密度函數表示屬性的不確定性[13]. 例如, 在位置服務中, 數據對象屬性A存在的情況是：i位置概率35%,k位置概率53%,j位置概率12%, 可見屬性A的值是不確定的, 但其所有可能值的概率之和為1.

2 AC-UDGen算法

針對屬性級不確定數據, 王建榮[14]進一步將屬性級不確定性數據分為屬性級離散不確定性和屬性級連續不確定性數據. 本文主要考慮屬性級連續不確定性數據, 定義為： 在m維空間m中, 給定不確定數據集O={o1,o2,…,on}和概率密度函數fi:m→, 如果將不確定數據對象ou的屬性Ai值記為ou[Ai], 用概率密度函數fi表示, 且滿足

則屬性Ai稱為不確定連續屬性.

由定義可知, 連續屬性級不確定數據的概率密度函數滿足一定的分布, 如均勻分布、高斯分布等. 針對屬性級連續不確定數據, 目前的生成算法[1-10]都未考慮到原始數據的分布特征, 如離群點等. 按目前算法進行轉化時, 不確定數據集的離群點數量會相應增加, 從而對不確定數據的挖掘帶來困擾; 此外, 在不確定數據生成過程中引入的擾動因子是固定不變的, 不能很好地體現數據的分布特征, 因此, 本文提出一種AC-UDGen算法, 該算法分為4步: 1) 在輸入的確定數據集上運行基于密度的局部離群點檢測-LOF算法[15], 計算出每個點的離群因子； 2) 由離群因子的大小判斷出該點周圍的密度大小, 并根據離群因子產生擾動因子； 3) 將擾動因子作為參數, 計算MBR值的大小； 4) 輸出不確定數據集. AC-UDGen算法流程如圖1所示.

圖1 AC-UDGen算法流程Fig.1 Flow chart of AC-UDGen algorithm

2.1 計算離群因子

離群因子是指數據集中每個對象的偏離程度, 根據每個對象的偏離程度可確定該對象是否為離群點. 實質上一個數據對象的偏離程度正是數據對象分布的表達, 偏離程度越高說明該對象周圍數據對象越少, 就最可能是離群點; 而偏離程度越低, 則該數據對象分布在較集中的局部區域中, 就不會是離群點. 本文采用LOF算法計算離群因子, 設D表示數據集,o,p分別為數據集D中的對象,k為正整數, 則離群因子的計算過程可分為3步, 下面以對象p為例進行說明.

1) 構建對象p的第k距離鄰域. 對象p的第k距離鄰域是指小于等于對象p最近的第k距離內的所有對象組成的集合. 實際上該集合反映了數據對象的偏離程度. 如果該集合較大, 說明該對象的第k距離鄰域較大, 則它的偏離程度就較大; 反之, 若集合較小, 則偏離程度就小. 其計算公式為

Nk(p)={q∈D{p}|d(p,q)≤k-dis(p)},

(1)

其中:d(p,q)表示數據對象p和數據對象q之間的歐氏距離；k-dis(p)表示對象p的第k近的距離,k為正整數.

2) 計算對象p的局部可達密度. 對象p的局部可達密度是指對象p的Nk(p)內所有對象平均可達密度的倒數, 計算公式為

(2)

如果至少有k個對像和p有相同的坐標值, 卻是不同的數據對象, 則式(2)的分母將趨近于0, 而對象p的局部可達密度將趨于∞; 相反, 如果數據對象p距離聚類簇較遠, 則其Nk(p)領域內所有對象的可達距離之和就會較大, 相應的lrdk(p)值則較小.

3) 計算對象p的離群因子. 結合式(1)和式(2)計算p的離群因子, 計算公式為

(3)

由式(3)可知, LOFk(p)的大小反映了數據對象p的第k距離范圍內空間點的平均分布密度, 易見, 若p的局部可達密度越小,p的Nk(p)內對象可達密度越大, 則對象p的LOF值越大. 即一個對象的LOF值越大, 則該對象是離群點的概率越大.

由式(1)～(3)可知, 離群因子的值反映了一個數據對象與其他對象間的分布關系, 并可根據其值的大小刪除異常點, 因此, 本文使用LOF的值經過適當處理作為不確定數據生成算法的參數.

2.2 計算擾動因子

結合離群因子確定β(0<β<1)的值. 在離群因子計算過程中, 如果一個對象的LOF值越大, 則其離群概率越大, 周圍的密度就較小, 落在其周圍的數據對象就較稀疏, 在AC-UDGen算法中, 其MBR值較大; 相反, 若一個對象的LOF值越小, 則該對象周圍區域就有更多的數據對象, 即落在其周圍的對象較密集, 在AC-UDGen算法中, 其MBR值較小. 所以, 本文使用下列公式計算擾動因子的值：

(4)

其中:βi表示第i個元組的擾動因子; LOFi表示每個對象的離群因子.

2.3 計算MBR值的大小

在原始數據集上, 先計算出每個數據對象的離群因子, 然后計算出每個對象的擾動因子β, 最后在數據對象的每一維上設置一個擾動區間,Ih=β×max_length, max_length表示所有對象在該維上的最大距離, 并使用擾動因子β控制每個數據對象對應的MBR值, 在每個MBR中隨機分布服從同一分布的固定數目的數據對象.

2.4 算法描述

AU-UDGen算法.

輸入: 確定數據集D,S(每條原始記錄所生成的不確定對象的個數);

輸出: 不確定數據集U.

1) 在D上運行LOF算法, 根據式(3)計算出每個數據對象的離群因子LOFi;

2) 根據LOFi及式(4), 計算出每個對象的擾動因子;

3) ① 對于數據集的每一維j;

② 對于數據集的每個對象i;

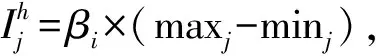
4) ① 對于每個數據對象i;

② repeat;

③ 對于每一維j;

④ 根據該維確定的值, 隨機生成滿足某個分布的不確定值Uij;

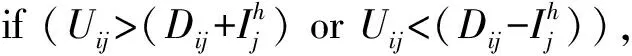
⑥ until每個數據對象都生成S條記錄；

5) 輸出不確定數據集U.

3 實驗結果分析

本文使用Python語言實現所提算法及涉及的相關算法, 版本為Python2.7.0. 運行環境為： Intel(R) Core(TM) i5-3470 CPU, 3.20 GHz, 8.00 GB內存, 操作系統為Windows8.1系統, 64位.

實驗分為3部分: 第一部分驗證AC-UDGen算法的準確率； 第二部分驗證不同概率密度函數對聚類結果的影響； 第三部分驗證AC-UDGen算法的時間效率. 實驗整體框架如圖2所示. 由圖2可見, 算法共分為5個過程, 由1)輸入確定數據集, 由2)運行本文算法, 將其變為3)中不確定數據集, 然后再統一使用4)中UK-means聚類算法進行聚類, 對結果使用5)中的評價標準, 分別從準確率和時間兩個維度驗證本文算法的有效性.

圖2 實驗整體框架Fig.2 Overall framework of experiment

1) 選取UCI機器學習數據集中的4種數據集作為原始確定數據集, 數據集屬性列于表1.

2) 對確定數據集, 運行本文提出的AC-UDGen算法, 將其變為不確定數據;

3) 得到不確定數據集;

4) 在不確定數據集上統一使用文獻[3]提出的不確定聚類算法UK-means進行聚類；

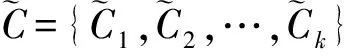
(5)

表1 UCI實驗數據集

F-measure針對的只是聚類結果, 而內部評價標準考慮到了聚類過程, 類內距表示聚類簇之間的緊密度, 類間距表示聚類簇間的分離程度. 類內距的計算公式為

(6)

類間距的計算公式為

(7)

其中, D(o,o′)表示數據對象o和o′的期望距離.

令Q(C)=inter(C)-intra(C)作為內部評價標準,intra(C)越小,inter(C)越大, 則聚類質量Q(C)越好. 由于intra(C)和inter(C)的值在[0,1]內, 則Q的范圍是[-1,1].

3.1 驗證AC-UDGen算法的準確率

采用文獻[6]和文獻[8]提出的不確定數據生成算法, 分別記為ABRAC算法和UK-medoids算法作為對比算法. 涉及的參數設S=100(S表示每個MBR內的樣本數),β=0.5. 對比算法只取其不確定生成算法, 聚類過程統一使用UK-means算法進行聚類. 概率密度函數采用uniform,normal,exponential,Laplace 4種分布. 在4種數據集上分別進行10次獨立實驗, 記錄每次的實驗結果, 并求出均值進行對比, 使用F-measure作為評價標準.

在不確定數據生成過程中, ABRAC算法首先在原始數據集的每一維上設置一個擾動區間Ih=0.1×max_length, 其中max_length表示所有點在該維上的最大距離, 然后使用擾動因子β(0<β<1)控制每個數據對象對應的MBR值大小, 且每個MBR內服從同一分布.

從上述兩種算法的生成過程可見, 在整個聚類過程中,β一旦選中就不再改變, 即β是固定不變的(UK-medoids中隨機選擇后也不再改變), 也即每個不確定數據對象的分布區域是確定的, 并未反映出數據對象周圍密度空間的分布情況, 如數據對象分布較密集, 則MBR的值也應該變小, 但由于β不變,Ih就不變, 導致MBR值也不變. 反之, 如果數據對象分布較稀疏, MBR值應該變大, 但由于β, MBR值不變. 所以β固定無法反應數據對象的分布特征. 而在AC-UDGen算法中, 首先對每個數據對象計算出其離群因子, 離群因子大表示數據整體分布稀疏,β也會變大, MBR值變大. 離群因子小, 表示密度大, 數據分布密集,β會變小, MBR值也變小, 更貼合數據的實際分布情況, 從而減少聚類的迭代次數, 提高運行效率. 圖3為3種不同算法在不同分布上的F-measure值比較. 由圖3可見, AC-UDGen算法的F-measure值, 除了在圖3(B)中的Wine數據集上與UK-medoids算法的F-measure值相同外, 在其他情況下AC-UDGen算法均優于ABRAC和UK-medoids算法.

圖3 3種不同算法在不同分布上的F-measure值比較Fig.3 Comparison of F-measure values of three different algorithms on different distributions

圖4 3種不同算法在不同分布上的Q值比較Fig.4 Comparison of Q values of three different algorithms on different distributions

F-measure是外部評價標準, 下面從內部評價標準出發, 比較各算法的Q值, 運行10次, 取均值, 結果如圖4所示. 由圖4可見, 在Wine數據集上, 采用uniform作為概率密度函數時, AC-UDGen算法的Q值低于UK-medoids算法, 但在其他情況下顯然高于另外兩種算法. 綜合F-measure和Q值兩種評價標準, 可知在多數情況下, AC-UDGen算法的聚類效果都優于其他兩種對比算法, 因此本文提出的算法是有效的.

3.2 不同概率密度函數對結果的影響

上述實驗結果表明, 不同概率密度函數會對聚類結果產生不同的影響. 下面選用normal, uniform,exponential,Laplace 4種分布進行實驗驗證, 在同一數據集上, 采用不同的概率密度函數, 分別運行10次, 結果如圖5所示. 由圖5可見, 在Iris數據集上, 采用uniform分布時結果波動較大, Laplace分布不適合Wine和Glass數據集, 而exponential分布也不適合于Glass和Ecoli數據集. 可見, 同一數據集采用不同分布時, 聚類結果不同； 在分布相同時, 數據集不同, 聚類結果也不同. 因此, 在生成不確定數據集時, 應對具體數據具體分析, 采用合適的概率密度函數.

圖5 不同數據集不同分布的聚類結果Fig.5 Clustering results of different data sets with different distributions

3.3 驗證AC-UDGen算法的時間效率

圖6 3種算法的運行時間對比Fig.6 Comparison of running time of three algorithms

圖6為3種算法的運行時間對比. 由圖6可見, AC-UDGen算法的執行時間比其他兩種方法長, 且對于3種算法隨著實驗數據集的規模增大, 執行時間也隨著延長. 雖然AC-UDGen算法有較高的時間代價, 但在可接受的范圍內, 獲得了較好的聚類結果.

綜上所述, 本文提出了一種屬性級連續不確定數據生成算法AC-UDGen, 通過引入離群點檢測算法, 計算每個數據對象的離群因子, 并將離群因子作為控制數據分布范圍的參數產生擾動因子, 降低了離群點對聚類結果的影響, 使每個數據對象MBR的值均可根據自身的分布特征自適應的變化, 可用于產生滿足任何已知分布的不確定數據對象. 通過實驗對比AC-UDGen算法與其他算法生成數據集上的準確率、聚類精度和執行時間, 也驗證了選擇不同的概率密度函數對聚類結果會有不同的影響, AC-UDGen算法可較好地彌補傳統算法的不足, 在可接受的時間內取得了較好的聚類精度.