使用因素對滾動輪胎振動特性影響的有限元分析

張穎文，王國林，周海超，楊 建

（江蘇大學 汽車與交通工程學院，江蘇 鎮江 212013）

汽車噪聲是交通噪聲的主要來源之一。相關研究表明，乘用車和商用車速度分別高于40和75 km·h-1時，輪胎的振動噪聲將成為車輛噪聲的主要來源[1]。而結構振動噪聲是載重子午線輪胎振動噪聲的主要部分[2-3]。因此，研究輪胎振動特性及其影響因素對低噪聲輪胎開發具有重要的意義。

輪胎振動噪聲產生的機理是其結構的振動引起周圍空氣的擾動通過空氣傳播到人耳[4]。J.Lin等[5]采用結構模態分析方法分析了輪胎振動特性與輻射噪聲之間的關系，結果表明，低階模態對輪胎振動輻射噪聲影響程度較大，并且峰值聲壓對應的頻率往往在輪胎固有頻率附近。Trong將輪胎簡化為包含剪切應力和非線性效應的圓環，通過有限元分析驗證了模型的準確性，并且用此模型分析了輪胎在非滾動和滾動狀態下的特性，得到不同速度下輪胎的固有頻率不同[6]。V.Q.Doan等[7]采用試驗測試和有限元分析相結合的方法研究胎面振動加速度與輪胎噪聲之間的關系，發現兩者之間關系顯著。包秀圖等[8]提出一種輪胎在滾動時頻域下的計算方法，將表面節點的振動速度轉化為聲學計算的頻域邊界條件，再利用聲學邊界元技術計算輪胎的低頻振動噪聲。蔡瓊陽[9]研究了輪胎的振動特性，發現輪胎的振動模態影響其聲輻射特性以及關系到車輛的多種性能。許志超等[10]采用試驗方法研究了輪胎通過噪聲與速度的關系，得到通過噪聲聲壓級與速度對數呈線性關系的結果。國內外學者研究了輪胎結構部件的振動對噪聲的影響，認為兩者之間存在緊密的聯系。因此，輪胎結構的振動特性可以成為振動噪聲的主要評價指標，用于研究輪胎的振動噪聲。

為了驗證滾動輪胎有限元模擬分析方法的有效性，選取215/75R17.5載重子午線輪胎為研究對象，將試驗和有限元仿真所得輪胎胎側各測點時域下的振動速度進行傅里葉變換。在此基礎上，研究輪胎使用因素對輪胎振動特性的影響，以期為解決輪胎在使用過程中遇到的噪聲和振動問題提供指導。

1 滾動輪胎有限元分析

1.1 有限元模型的建立

利用文獻[11]中的方法建立有限元模型，如圖1所示。模型中輪輞和路面定義為解析剛體，橡膠部分采用CGAX3和CGAX4R單元模擬，鋼絲簾線采用SFMGAX1和REBAR單元模擬。分析時，輪胎的載荷為10 000 N，充氣壓力為0.83 MPa。

圖1 輪胎三維有限元模型

橡膠的本構模型通過單軸拉伸試驗獲得，將測得的橡膠拉伸數據輸入Abaqus中，利用其自帶的Ogden，Neo-Hookean和Yeoh等橡膠本構模型分別進行擬合。以胎肩墊膠為例，其材料應力-應變曲線參照文獻[12]，在名義應變小于0.5時，Yeoh模型擬合的應力-應變曲線與試驗結果吻合較好。因此，本研究選用Yeoh模型描述輪胎橡膠的力學特性。輪胎各部位的膠料參數由單軸拉伸試驗數據擬合獲得。

1.2 滾動輪胎數值仿真

利用Abaqus/Explicit模擬輪胎在30 km·h-1速度時的滾動過程。為分析滾動輪胎胎側的振動特性，在胎側上布置4個振動測試點，如圖2所示。4個測點分布在與接觸區域夾角為45°，135°，180°和315°的位置。測點1為接地后端，測點4為接地前端。有限元分析得到各測點時域下的振動速度如圖3所示。

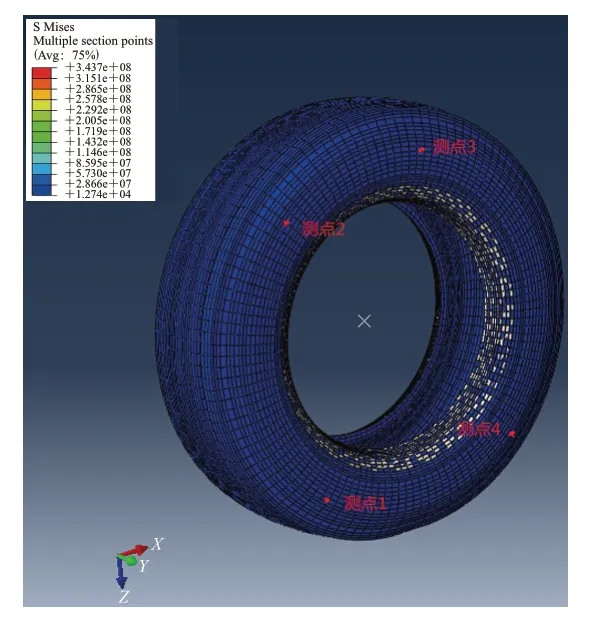
圖2 有限元模型胎側測點位置

從圖3可以看出：測點與接地區域距離越近，振動速度幅值越大；接地后端的振動比接地前端劇烈。

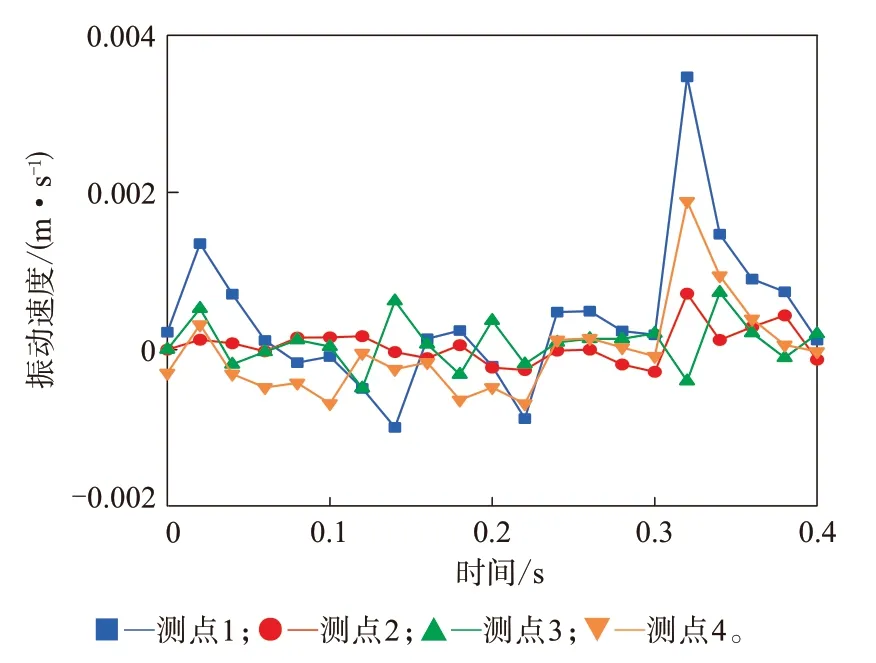
圖3 不同測點時域下的振動速度

2 滾動輪胎胎側振動試驗

2.1 輪胎振動響應試驗

滾動輪胎胎側振動特性試驗是在轉鼓試驗臺上進行的，如圖4所示。試驗時輪胎載荷為10 000 N，充氣壓力為0.83 MPa，測量速度為30 km·h-1。采用單點式多普勒激光測振儀測量輪胎胎側的振動特性。為與有限元分析結果進行對比，振動測試點的布置與有限元分析一致。

圖4 輪胎振動試驗

試驗時將多普勒激光測振儀固定在三腳架上，并將其通過數據采集器與電腦連接，如圖5所示。三腳架距離被測輪胎大約50 cm，將激光束打到胎側測點上，旋轉調焦旋鈕，當激光點最小、最亮時最佳，依次調節三腳架的位置分別對不同測點進行測量。

圖5 多普勒激光測振儀

采樣時間（ts）和頻率（fs）分別設置為

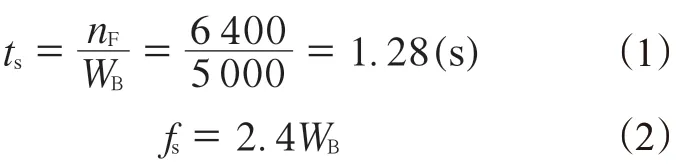
式中，nF為頻譜數，WB為帶寬。測試時對每個測點多次測量，結果取平均值。為了方便與有限元分析結果進行對比，對試驗數據進行濾波。濾波時采用Matlab中等波紋低通濾波器Firpm函數，其通過頻率為20 Hz，截止頻率為500 Hz。圖6示出了隨機測點濾波前后的振動速度對比結果。

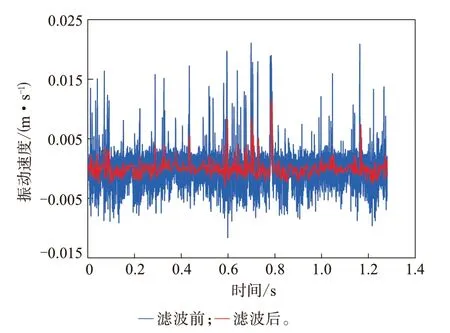
圖6 測點濾波前后振動速度對比

從圖6可以看出，濾波前后曲線的波動趨勢大致相同，峰值分布也類似。

2.2 結果與分析

圖7和8分別示出不同測點振動速度以及接地前后端測點振動速度的對比情況。

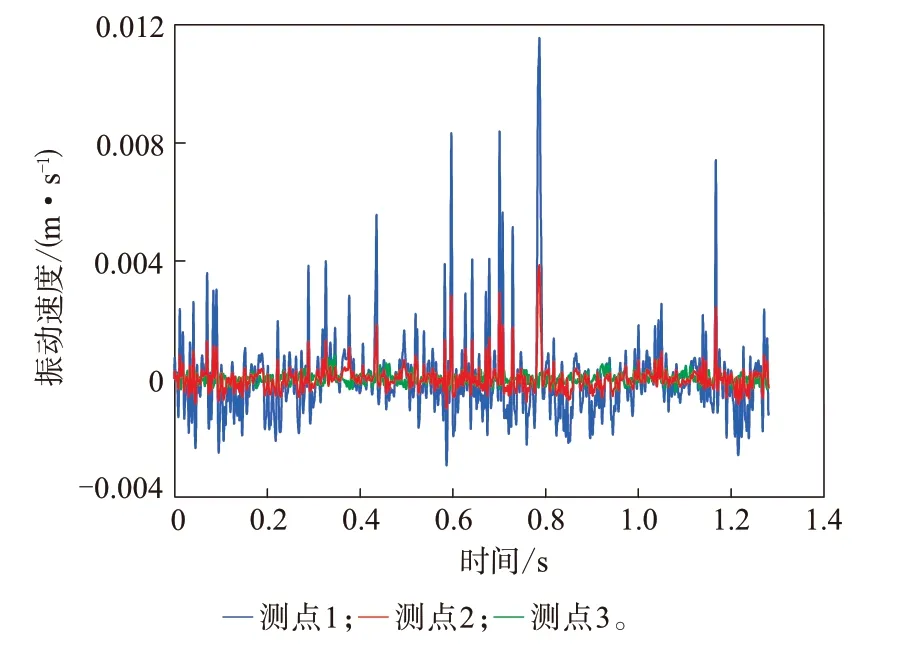
圖7 不同測點的振動速度

從圖7可以看出，在相同速度下，測點1，2和3的振動速度幅值呈遞減的趨勢，這說明越靠近接地區域，胎側的振動越劇烈。這與文獻[13]中靠近接地區域聲能量分布高表明該區域振動劇烈的結論相一致。從圖8可以看出，輪胎接地后端的振動響應大于接地前端，接地前端振動速度的峰值明顯小于接地后端。文獻[14]采用室內轉鼓試驗測試載重子午線輪胎近場噪聲，結果表明，輪胎接地后端的振動噪聲聲壓級大于輪胎接地前端的振動噪聲聲壓級，而振動噪聲聲壓級與振動劇烈程度呈正相關性，這一結果與試驗結果相一致。

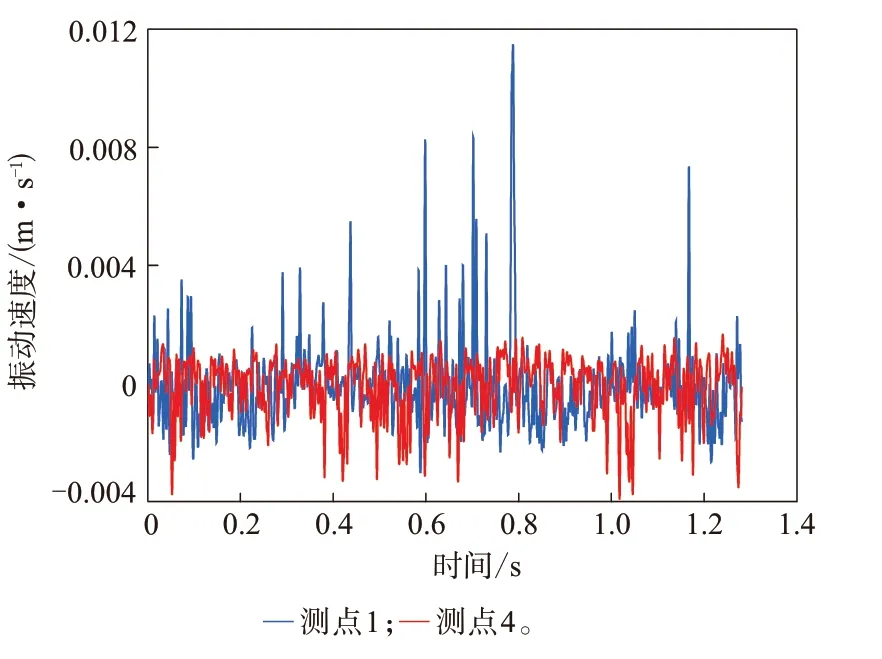
圖8 接地前后端測點的振動速度

不同測點時域下實測結果與有限元仿真結果的對比情況如圖9所示。

從圖9可以看出，3個測點時域下的振動速度曲線變化趨勢一致。為了更好地將實測值與仿真值進行比較，將時域下的信號進行離散傅里葉變換，得到頻域下的振動速度曲線，結果如圖10所示。可以看出，胎側測點試驗和仿真得到的振動速度在頻域下的分布具有良好的一致性，證明所建滾動有限元模型有效。

圖9 不同測點時域下振動速度實測值與仿真值對比

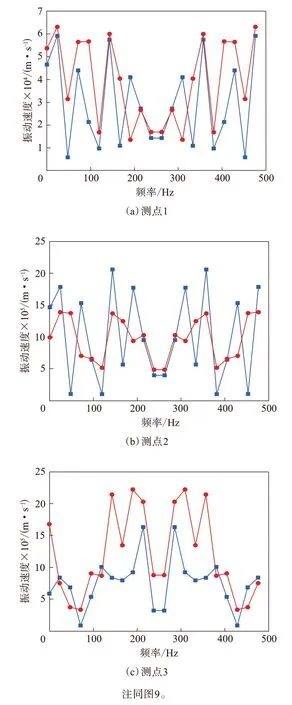
圖10 離散傅里葉變換后不同測點頻域下振動速度實測值與仿真值對比

3 使用因素對輪胎振動特性的影響

為分析輪胎使用因素對振動特性的影響，采用單一變量法，研究速度、充氣壓力和載荷對胎面和胎側振動特性的影響規律。

3.1 滾動速度

在輪胎充氣壓力和載荷均為額定值的情況下，研究不同速度下胎側和胎面圓周上振動速度分布，結果如圖11所示。

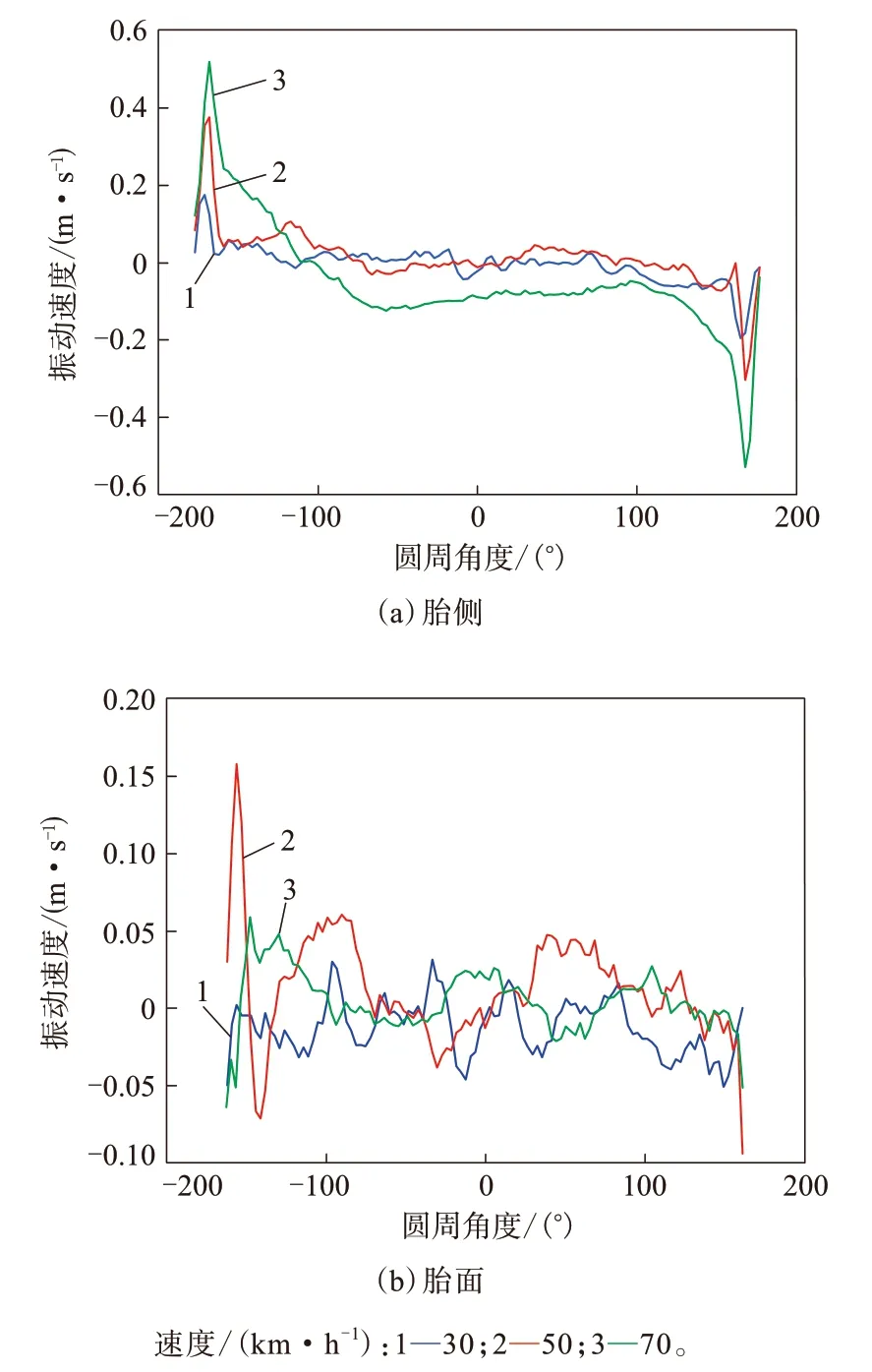
圖11 不同速度下輪胎圓周上振動速度分布

圖11中坐標軸原點代表輪胎上頂點位置，沿著X軸正方向為輪胎接地前端方向圓周區域，負方向為輪胎接地后端方向圓周區域，圖形兩邊端點即為輪胎的接地中心點。從圖11（a）可以看出：胎側圓周振動速度分布近似關于原點對稱；隨著速度的增大，胎側的振動速度也隨之增大，在±169°的圓周上出現峰值，在－150°～150°范圍內振動幅值較小，且趨于平緩。從圖11（b）可以看出，隨著輪胎滾動速度增大，胎面部分的振動速度也隨之增大，不同速度下胎面振動速度總體波動較大，在±153°圓周點上出現峰值。胎側、胎面接地后端的振動速度均大于接地前端的振動速度。

3.2 充氣壓力

在輪胎滾動速度一定（70 km·h-1）和載荷為額定負荷的情況下，研究不同充氣壓力下胎側和胎面圓周上振動速度分布，結果如圖12所示。

從圖12（a）可以看出：胎側圓周振動速度分布關于原點對稱；隨著充氣壓力的增大，胎側的振動速度也隨之增大，在±169°的圓周上出現峰值，在－150°～150°范圍內振動幅值較小，且趨于平緩。從圖12（b）可以看出：0.9倍額定充氣壓力和額定充氣壓力下胎面的振動速度大致相等，1.2倍額定充氣壓力下胎面振動速度最大；不同充氣壓力下胎面振動速度總體波動較大，在±153°圓周點上出現峰值。胎側、胎面接地后端的振動速度均大于接地前端的振動速度。

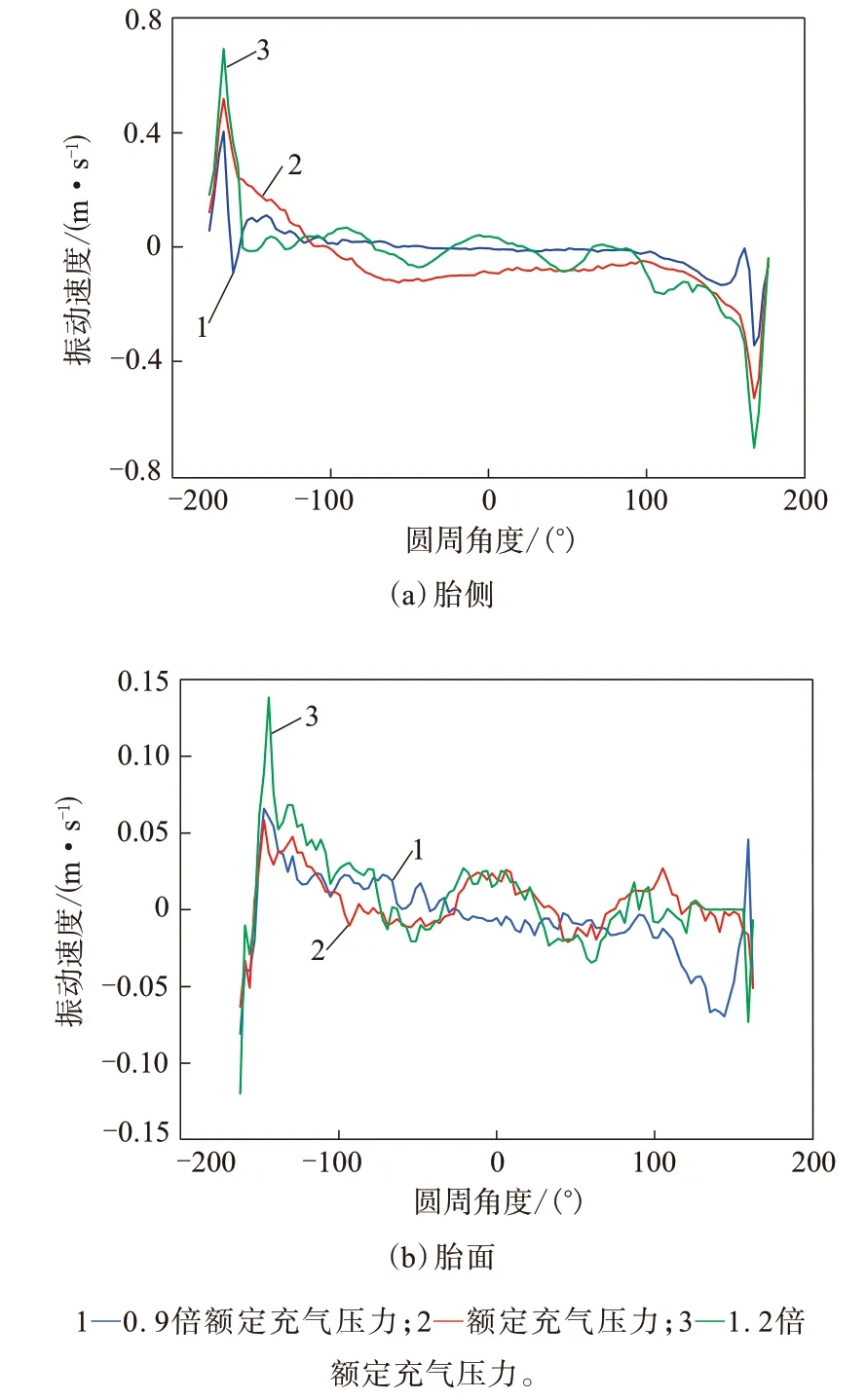
圖12 不同充氣壓力下輪胎圓周上振動速度分布

3.3 載荷

在輪胎滾動速度一定（70 km·h-1）和額定充氣壓力的情況下，研究不同載荷下胎側和胎面圓周上振動速度分布，結果如圖13所示。

從圖13（a）可以看出：胎側圓周振動速度分布近似關于原點對稱；隨著載荷的增大，胎側振動速度變化量較小，在±169°的圓周上出現峰值，在－150°～150°范圍內振動幅值較小，且趨于平緩。從圖13（b）可以看出，胎面振動速度隨著載荷的增大變化較小，但波動較大。胎側和胎面接地后端的振動速度均大于接地前端的振動速度。

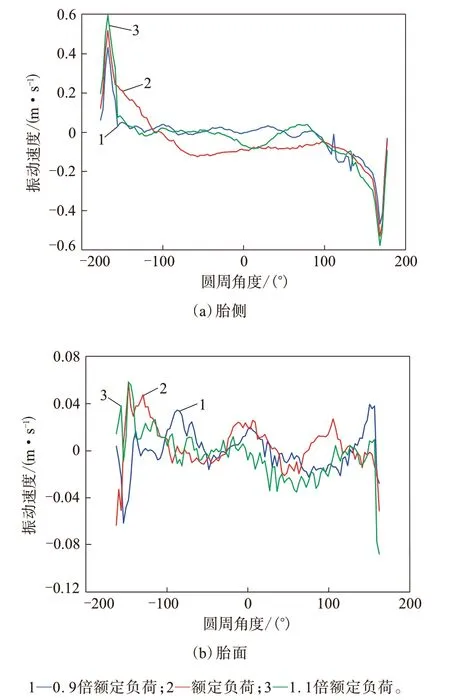
圖13 不同載荷下輪胎圓周上振動速度分布

4 結論

（1）輪胎滾動有限元模型胎側測點頻域下的振動速度與輪胎轉鼓試驗時胎側的振動速度具有良好的一致性，驗證了輪胎滾動有限元模型的準確性。

（2）胎面的振動速度分布關于輪胎頂點對稱，靠近接地區域振動速度幅值最大，接地后端振動速度大于接地前端；隨著速度和充氣壓力的增大，胎面和胎側的振動速度隨之增大，載荷對胎面和胎側振動速度的影響較小。