基于三次樣條函數的長線路GNSS高程擬合研究

張海燕，李秀海,韓 冰

(1.廣東省佛山市南海區房地產測繪中心,廣東 佛山 528220 ;2.黑龍江工程學院 測繪工程學院，黑龍江 哈爾濱 150050;3.哈爾濱測量高等專科學校測量工程公司，黑龍江 哈爾濱 150050；4.黑龍江測繪地理信息局 地理信息工程院，黑龍江 哈爾濱 150081)

GNSS高程擬合仍是目前測繪工程技術研究的熱點，并取得了可喜的研究成果[1-9]。公路測繪GNSS高程擬合不斷有測繪科技工作者進行理論研究和實踐探索[10-12]。公路測繪具有測區狹窄和線狀的特點，且高程控制測量等級以四等和等外水準測量為主。在面狀、線狀測區具有較多高等級高程控制點的情況下，已有的GNSS高程擬合研究成果已證明能夠達到四等或更好的精度。由于國家已有高等級測量控制點破壞較嚴重，外業公路控制測量能夠利用的高級水準點并不多，在高程起算點數量較少和擬合線路較長的情況下研究GNSS高程擬合的精度和可靠性更具有實際應用價值。已有公路GNSS高程擬合研究成果多以分區、分段，以線性、曲線模型擬合，需要較多的高程起算數據，實際工程很難滿足。三次樣條函數具有連續光滑的特點，對一些連續光滑的曲線物理模型具有很好的擬合效果，而線狀區域大地水準面具有連續光滑的特性，因此利用三次樣條函數對線狀GNSS高程擬合具有很好的適應性。本文利用某道路改擴建工程的一級GNSS和四等高程控制網的工程實例，基于三次樣條函數對GNSS高程擬合進行了研究，得到了一些有益的結論。

1 公路GNSS高程擬合常用的數學模型

公路GNSS高程擬合常采用以下線性模型、二次曲線模型和三次曲線模型：

ξ=a0+a1x,

(1)

ξ=a0+a1x+a2x2,

(2)

ξ=a0+a1x+a2x2+a3x2,

(3)

ξ=H大-h正.

(4)

式中:ξ為高程異常;x為擬合坐標(或是設計公路的里程數)。通過公共點的大地高和正常高，根據最小二乘原理可求出式(1)—式(3)中的系數ai，進而可求出擬合點的高程異常及正常高。

2 三次樣條函數及三彎矩方程

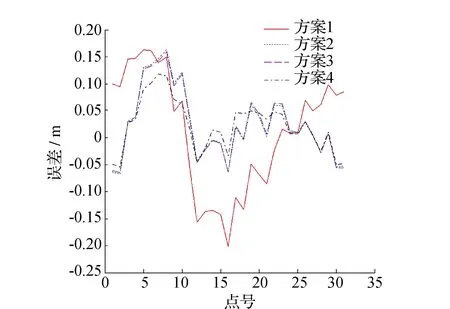
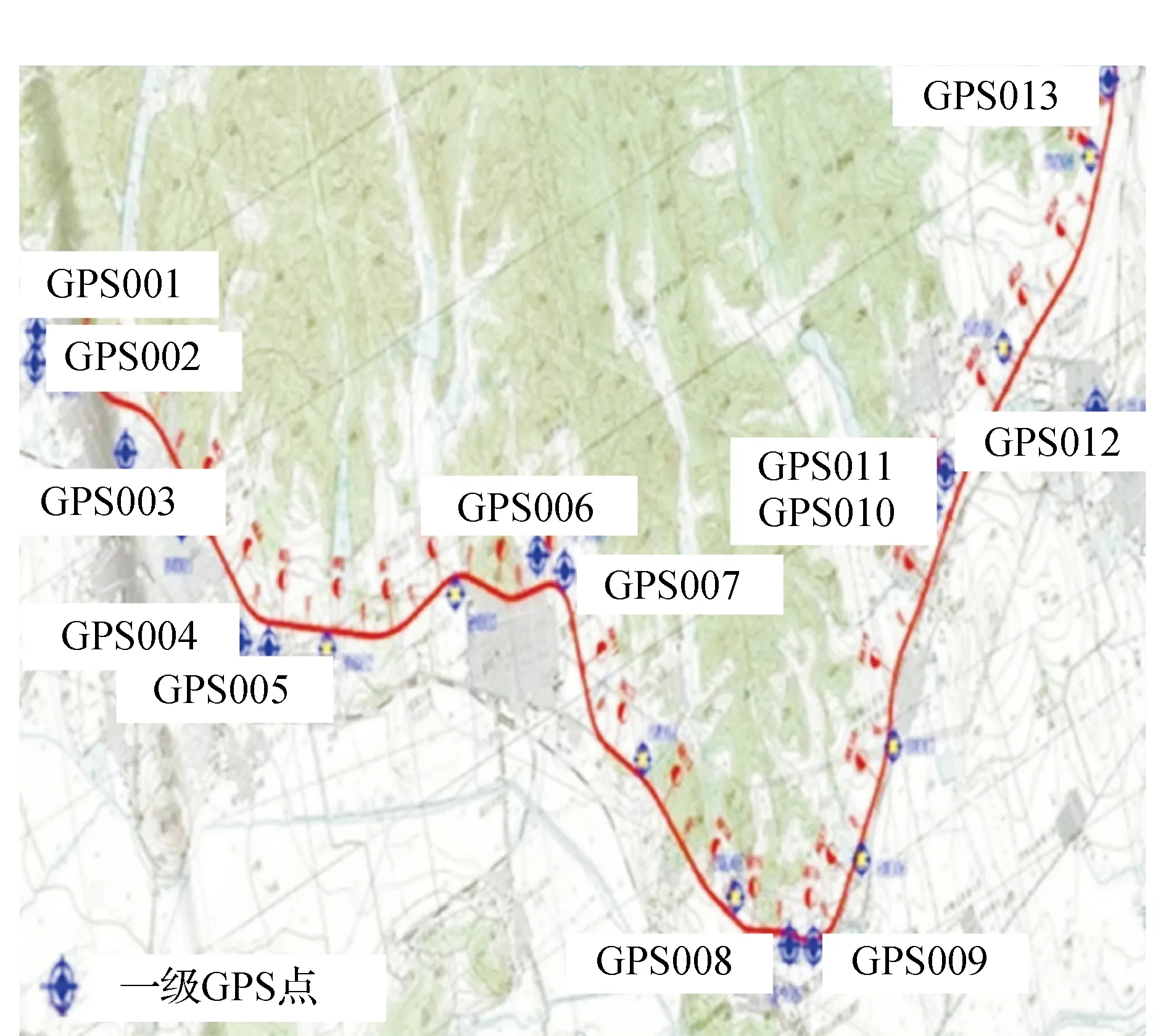
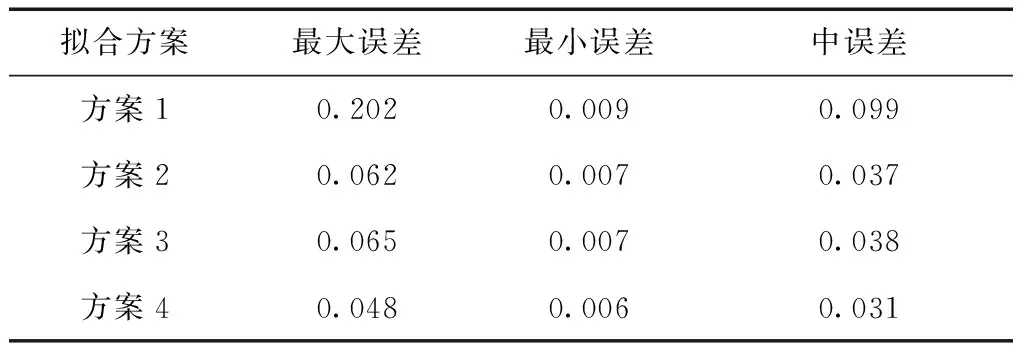
設有一剖分Ω，p1=x1

B(x)∈C2[p1，p2](即B(x)在閉區間[p1，p2]具有連續的一階、二階導數)。

B(x)在每一個子區間[xi,xi+1]上(j=1,2,…，n-1)是次數≤3的多項式，則稱B(x)為關于剖分Ω的一個三次樣條函數[13]。

設有函數f(x),其函數值表(xi，f(xi))，(i=1,2，…，n),如果三次樣條函數B(x)滿足插值條件

B(xi)=f(xi),(i=1,2,…,n).

稱B(x)為f(x)的關于剖分Ω的三次樣條插值函數。分段三次多項式函數可由Hermite插值函數表示，即B(x)在[xi,xi+1]的表達式為

B(x)=Bi(x)=yi+ai,1(x-xi)+

ai,2(x-xi)2+ai,3(x-xi)3.

(5)

(6)

其中Di是三次樣條函數B(x)在節點處的二階導數，即

B″(xi)=Di,(i=1,2,…,n).

確定三次樣條函數需要求解Di，在滿足自然邊界條件D1=Dn=0的條件下，其它Di由下式求解

(7)

其中，

(8)

方程中的未知量Di在力學上解釋為細梁在xi截面處的彎矩，且彎矩與其相鄰兩個彎矩有關，故方程(7)稱為三彎矩方程。由方程(7)求出Di后，帶入式(6)，即可確定三次樣條差值函數。

3 實例分析

某高等級公路改擴建工程需要建立一級GNSS工程控制網和四等水準高程控制網。按規范要求，每5 km左右布設1對控制點，設計公路線路長度約83 km，全網共布設31個一級GNSS點，聯測三等以上水準點5個，每個新布設的一級GNSS點均聯測四等水準。線路約東西走向，故高程擬合以橫坐標作為自變量。5個高級水準點分割的4段擬合路線長度由西向東分別為25 km、15 km、20 km、23 km。西部第1段經過礦區和山區，地貌起伏較大，最大高差約100 m，其余3段地勢較平坦。GNSS控制網外業采用徠卡1 200雙頻GNSS接收機觀測，采用邊連接方式，每時段觀測45 min以上，內業使用LGO軟件解算，獲得合格的三維無約束平差結果，并進行高程擬合計算。

設計如下4種高程擬合方案：

方案1：利用線性函數式(1)作為高程擬合模型；

方案2：利用二次曲線式(2)作為高程擬合模型；

方案3：利用三次曲線式(3)作為高程擬合模型；

方案4：利用基于三彎矩方程的三次樣條函數進行高程擬合。

各種擬合方案及精度統計見表1和圖1，擬合精度統計由式(9)計算。

(9)

其中，H正為正常高；H擬為擬合高程；n為擬合點的個數。

表1 全線路GNSS高程擬合誤差精度統計 m

注：共31個點

圖1 高程擬合誤差曲線

由表1可看出，方案1利用線性模型進行高程擬合精度最低，而方案2和方案3分別采用二次曲線模型和三次曲線模型進行高程擬合精度基本相當，比方案1擬合精度有明顯提高。方案4利用三次樣條函數進行高程擬合中誤差為4.6 cm，明顯優于其它幾種方法，表明用三次樣條函數進行高程擬合是成功的。由圖1可看出，方案4高程擬合誤差曲線較平滑，震蕩較小，顯示該方法的優越性。在四種方案中，方案1高程中誤差達dm級，表明對較長線路的GNSS高程擬合用單一的線性模型擬合是不合適的。其它幾種方案擬合精度均高于方案1，達到cm級，擬合精度能夠滿足一般的測圖需要，在實際公路勘察測量中可以選用。方案4在擬合線路較長、高程起算點較少的情況下，總體擬合精度小于5 cm，且擬合誤差曲線較平滑，更接近于大地水準面的實際情況，具有較好的擬合效果。認真分析各方案，發現在線路的第1段(見圖2，最西邊2個高程起算點之間的設計路線)擬合誤差最大，其余3段擬合效果均較好，分段統計精度如表2、表3所示。

圖2 第1段公路線路

表2 第1段線路GNSS高程擬合誤差精度統計 m

注：共10個點

表3 其余3段線路GNSS高程擬合誤差精度統計m

注：共21個點

由表2、表3可看出，除方案1外，其它3種擬合方案第1段擬合的誤差均較大，而其余3段擬合的中誤差均小于4 cm。究其原因，主要有三：一是第1段線路兩端高程起算點之間的線路長近25 km，線路較長；二是該段線路高差起伏較大，路線經過山區和礦區，大地水準面變化較大，期間僅有2個高程起算點很難準確擬合；三是該段線路非直線，呈U字形，而擬合坐標是以橫坐標為自變量，與假定線路基本直線實際差別較大，但利用三次樣條函數插值擬合精度仍達到cm級。

4 結束語

利用三次樣條插值函數進行線路高程擬合，在擬合線路較長及高程起算點較少的情況下，仍能達到cm級的擬合精度。在地勢較平坦地區，利用二次曲線和三次曲線進行線路高程擬合，擬合精度沒有太大差別。在地形和線路變化較大地區，各種模型擬合誤差均較大，如何提高此類線路的GNSS高程擬合精度需進一步研究。