坐標系轉換中基于象限分布的公共點選取方法

李金濤，王 微,石 波

(山東科技大學 測繪科學與工程學院，山東 青島 266590)

在工程應用中，實現坐標系統的變換與統一問題，需已經變換參數進行坐標轉換。提高坐標轉換參數精度方面，牛琳等提出逐步剔除精度不高和分布不合理的公共點的方法[5]；王玉成等提出分區轉換的方法[6]，這兩種方法都有效地提高轉換參數的求解精度，但對公共點的數目要求較高，需要布設和施測大量的公共點；兼顧轉換參數的求解精度和公共點數量，尹暉等提出了有效面積分析法[7]，可以減少公共點的數量且保證轉換參數的求解精度，但該方法主要考慮三維公共點在水平面上分布的合理性，對于在垂直面上的分布考慮較少，存在一定缺陷。因此本文提出了基于象限分布的公共點選取方法，充分考慮到二維及三維坐標系中公共點的數量及空間分布的幾何特征。實驗證明，利用該方法選擇的公共點求得的轉換參數精度高且數量少，對公共點的布設、選取具有指導作用。

本文介紹了四參數平面坐標轉換和七參數空間坐標轉換的方法，然后詳細論述了平面坐標轉換和空間坐標轉換中一種基于象限分布的公共點選擇新方法，最后為驗證該方法的可行性，利用模擬數據分別在平面坐標系和空間坐標系下進行可行性分析。

1 坐標轉換模型

1.1 平面四參數坐標轉換模型

四參數模型是從布爾莎模型演化而來的，其計算式為

(1)

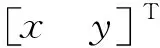
1.2 空間七參數坐標轉換模型

設有兩個空間直角坐標系，坐標原點不同，空間尺度不同，3個坐標軸也互不平行，將其中一個坐標系下的某空間點A轉換到另一個坐標系下，需要計算兩坐標系之間的7個轉換參數，包括3個旋轉參數εx，εy，εz，3個平移參數ΔX,ΔY,ΔZ和一個尺度因子λ。這7個參數與兩空間直角坐標系中公共點坐標之間的關系[8-9]：

(2)

若已知兩坐標系中至少3個公共點的三維坐標，可利用最小二乘原理求解7個轉換參數的最或然值。若將原坐標系依次繞Z軸、新的X軸和新的Y軸進行旋轉，則相應的旋轉矩陣為

2 基于象限分布的公共點選取方法

2.1 平面坐標轉換中公共點的選取

基于象限分布的公共點選取方法主要考慮了公共點的幾何分布對求解結果的影響，在公共點點位精度相同的條件下，公共點分布比較密集時，從幾何角度上來講，各點與原點所成直線間夾角過小；從向量線性關系的角度來看，相當于各點所成向量接近于線性相關。因此公共點分布不合理時容易導致轉換參數解算過程中法方程的病態性，其程度可用條件數K表示[10-12]。公共點分布越離散，點位幾何強度越好，K值越小，求解精度越高；反之求解精度越低。點位分布將直接影響參數求解精度。基于象限分布的公共點選取方法是根據公共點在坐標象限中的分布情況，選取出分布盡可能離散的一定數目的公共點參與計算，以提高點位的幾何強度，從而提高參數求解精度。平面坐標轉換中假設原坐標系下有如圖1所示分布的公共點，利用公共點象限分布的方法選取公共點。

1)對各公共點的Χ坐標和Y坐標取平均值，將坐標原點O移到均值處，完成公共點坐標的重心化；

2)在四個象限中，分別找到該象限中距離坐標原點最遠的點，即圖2中P1,P2,P3,P44點，并計算它們各自到坐標原點的距離d1,d2,d3,d4；

3)取d1,d2,d3,d4的平均值d，以坐標原點為圓心，以d為半徑做圓，用該圓邊界所在的區域表示初始概略搜索區域，如圖3中的實線圓所示；

4)根據公共點間的平均距離s確定搜索參數L，L=k×s，k為實數，初始值可取為1。半徑為d+L和d-L的圓之間的區域即確定為初始搜索區域，如圖3中兩虛線圓之間的區域，該區域內的點最先被搜索到。

5)計算每個象限中初始搜索區域內公共點到該象限中線(圖4中實對角線)的距離，距離中線最近的公共點視為滿足條件的公共點，完成一次搜索；

6)若初次搜索后搜索到的公共點數目大于最終需要的數目，則適當減小k值以縮小初始搜索范圍再次搜索；反之則增大k值，從而擴大初始搜索范圍繼續進行搜索，直到搜索到滿足數目要求的公共點。

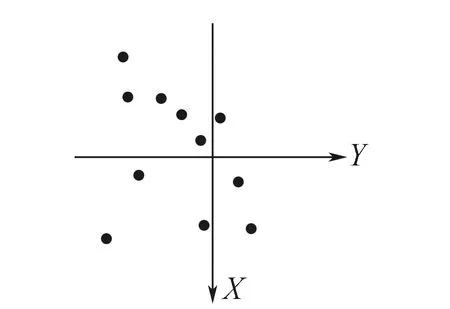
圖1 平面公共點分布

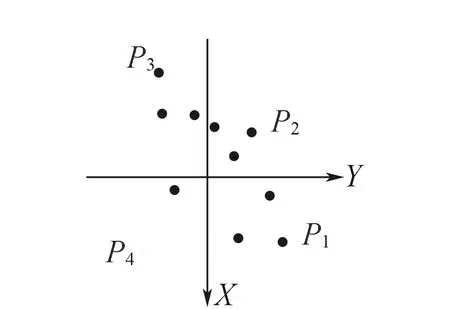
圖2 重心化后公共點分布

圖3 初始概略搜索區域

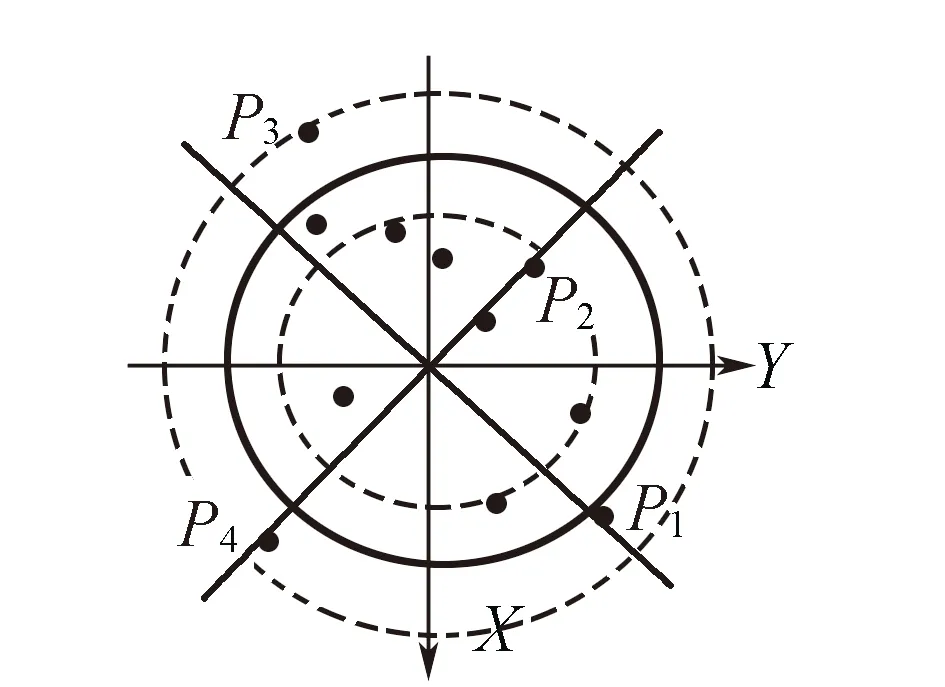
圖4 象限中線與搜索區域

平面坐標轉換至少需要兩個公共點，由于該方法搜索得到的公共點分布具有最佳性，因此從3個或4個象限中搜索3～4個公共點求解的轉換參數就具有很高的精度。

2.2 三維坐標轉換中公共點的選取

將二維平面拓展到三維空間，基于公共點象限分布的選擇方法從8個象限中搜索一定數目的公共點，使得這些公共點的幾何強度最高。公共點的選擇方式與二維空間中類似，假設在三維空間下，兩坐標系中有7個公共點，分別為P1～P7，它們在8個象限的空間分布如圖5所示，為形象地表示點與點之間的位置關系，在圖6中表示在XY平面內的投影圖。

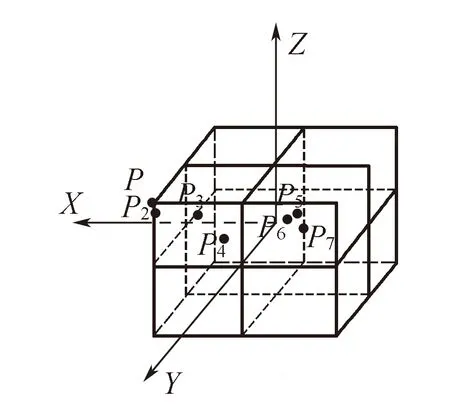
圖5 三維空間公共點分布

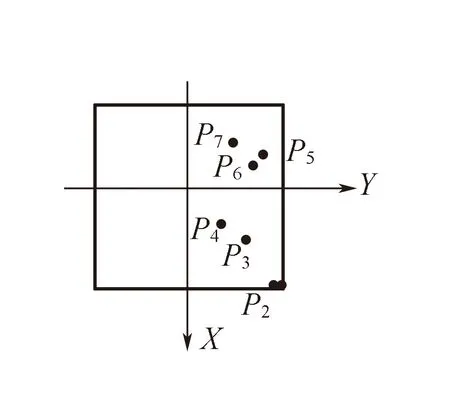
圖6 公共點的平面投影

基于象限分布的公共點選擇方法：對7個公共點進行坐標重心化，使得7個公共點在8個象限中盡量均勻分布；確定初始概略搜索區域，概略搜索區域為一球面，球心在坐標原點，半徑為各個象限中與坐標原點相距最遠點的平均值。初始概略搜索區域在XY平面內的投影如圖7中虛線圓所示；確定初始搜索區域，在三維空間中，初始搜索區域為兩個同心球體的非公共部分。兩同心球與第一象限的位置關系如圖8所示，P1，P2兩點位于此象限初始搜索范圍內；從每個象限中搜索距離該象限中線(圖8中虛對角線為第一象限的中線)最近的點作為搜索到的公共點，盡量使得搜索到的點所在的象限互不相鄰。若第一次搜索后滿足條件的公共點數目多于最終需要的公共點數目則適當減小k值以縮小初始搜索范圍；反之則增大k值，擴大搜索范圍，循環搜索，直到搜索到最終需要數目的公共點。

要求得7個坐標轉換參數需知道至少3個公共點，利用基于公共點象限分布的方法指導空間坐標轉換公共點選取時，可以找到分布合理且盡量少的公共點，使得用少量的點求得的結果與大量的點求得結果相當甚至精度更高。

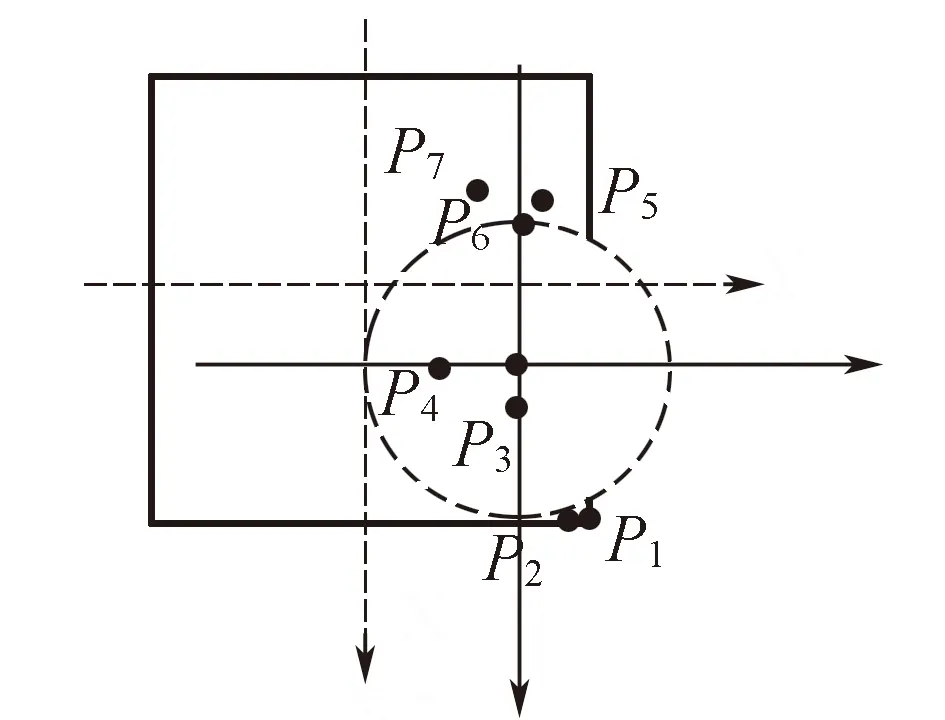
圖7 初始概略搜索區域

圖8 第一象限搜索區域

3 實驗分析

3.1 平面坐標轉換公共點選取實驗

假設在兩平面坐標系中有7個公共點，它們在原平面直角坐標系中的分布如圖9所示，坐標值如表1所示。對7個公共點先繞坐標原點旋轉10°，再分別沿X，Y軸方向平移10 m，20 m，得到目標坐標系下的坐標，對目標坐標系下的坐標加上σ=5 mm的高斯白噪聲擾動。

圖9 原平面公共點分布

公共點點號P1P2P3P4P5P6P7X坐標值/m-50-45-40-40-101020Y坐標值/m50604010-201030

若從7個公共點中選出3個參與求解轉換參數的平差計算，利用本文提出的方法選出的3個公共點為P3,P4,P7，對應的公共點組合序號為28(表2列出了組合序號與公共點組合方式的對應關系)。為表示其求解精度，利用未參與計算的點檢驗所求的轉換參數，并計算標準差σ。

Δs2=Δx2+Δy2.

(3)

任意3個公共點參與計算時求得的方程條件數、標準差、平移誤差和角度旋轉誤差如表3所示，其中組合序號為36的表示利用7個公共點共同求解的結果，將此結果作為參考值，對應的標準差由7個點求得。

表2 公共點組合序號與公共點組合方式的對應關系

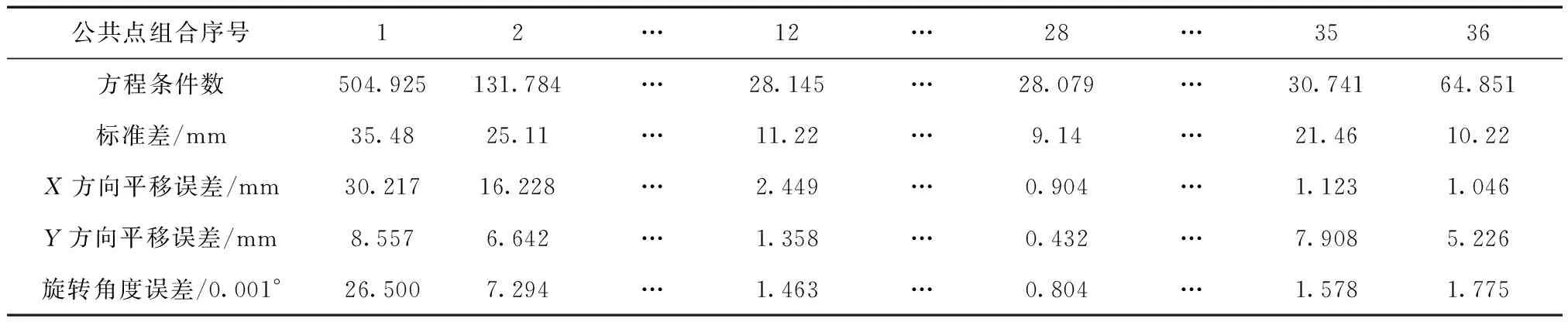
表3 平面坐標轉換公共點組合方式與對應的求解結果

為比較求解結果的精度，將各種組合方式下求得的結果繪制成圖10所示的直方圖。從圖中可以看出，標準差、角度和距離參數誤差與方程條件數有一定關系，條件數較小時標準差較小，角度和距離的求解誤差也均較小，反之條件數較大，標準差變大，角度和距離的求解誤差至少有一個較大。即反映了公共點分布幾何強度的好壞對求解結果精度的影響，當公共點分布合理時條件數較小，對應的參數求解精度及坐標轉換精度也較高。

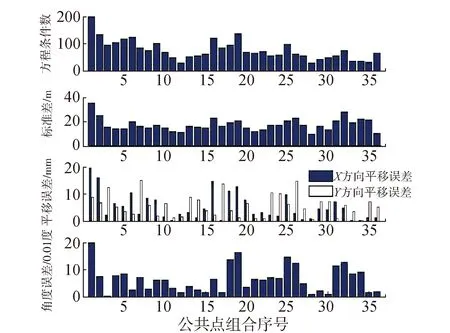
圖10 平面坐標轉換各種求解結果

從圖10中可以看出方程條件數較小的組合序號為12和28，即這兩種組合公共點的幾何強度高，再通過比較標準差和轉換參數誤差可知，組合序號為28的求解精度較高，這與利用本文的方法選出的公共點組合方式一致，且只用了3個公共點參與計算，減少了所需公共點的數量。

3.2 三維坐標轉換公共點選取實驗

假設在兩空間直角坐標系中有7個公共點，在原空間坐標系中的分布如圖11所示，坐標值如表4所示。對7個公共點分別繞X,Y,Z軸旋轉20°,40°,60°，再分別沿X,Y,Z軸方向平移10 m,20 m,30 m，得到目標坐標系下的坐標，對目標坐標系下的坐標加上σ=5 mm的高斯白噪聲擾動。

圖11 原三維空間公共點分布

公共點點號P1P2P3P4P5P6P7X坐標值/m100-1001001003080-10Y坐標值/m10010010095-3060-20Z坐標值/m100100-100-95-304020

從7個公共點中選出3個來求解7個轉換參數，并計算它們的真誤差。利用本文提出的方法選取到的公共點為P1,P2,P33個點，對應的組合序號為1(見表5)，各種組合方式所求得的條件數、標準差和七個轉換參數誤差如表5所示。

表5 三維坐標轉換公共點組合方式與對應的求解結果

為分析各種組合方式下的求解精度，將各種組合方式下求解的條件數、標準差、平移誤差和旋轉角度誤差繪制成如圖12所示的條形圖。

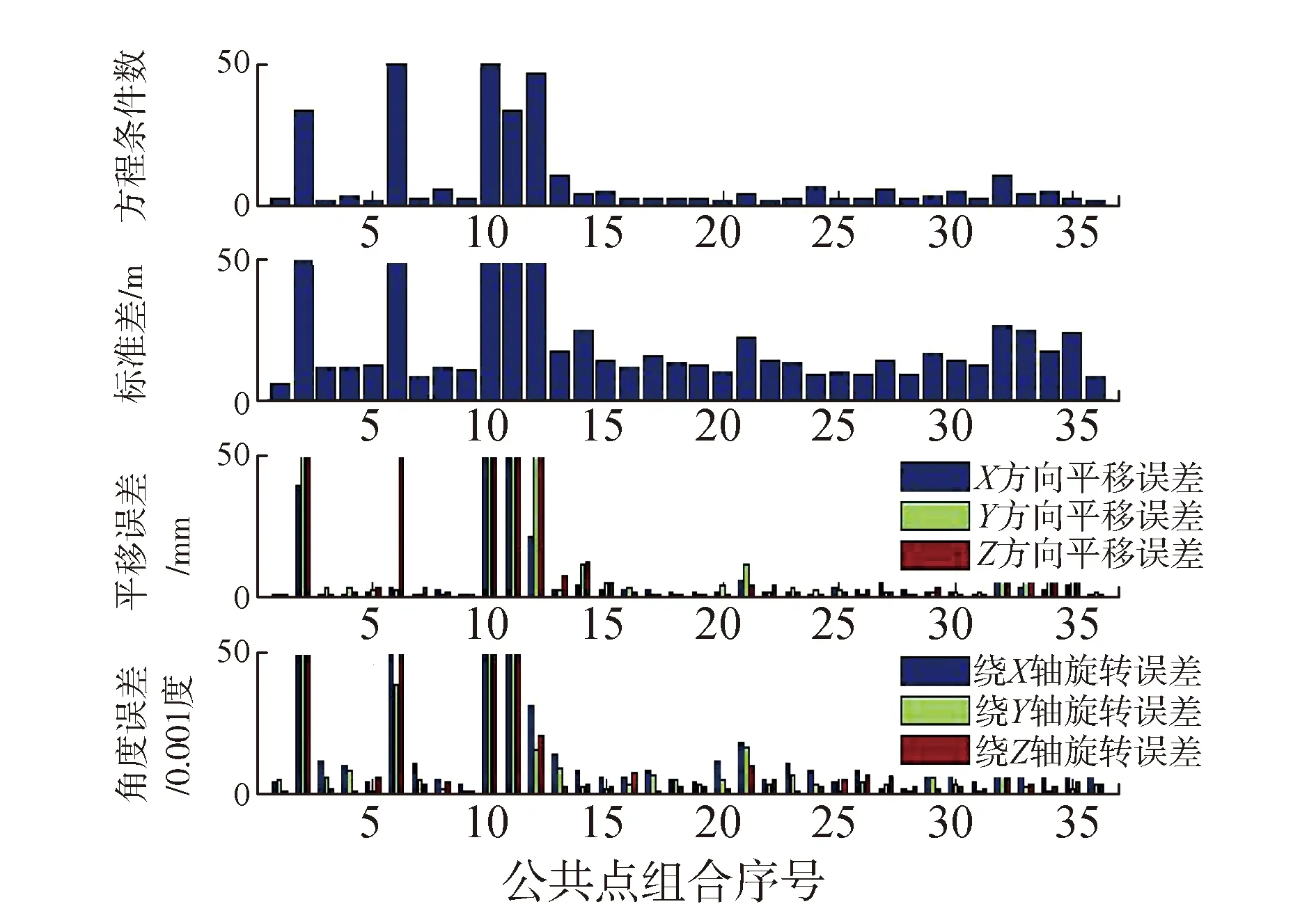
圖12 三維坐標轉換各種求解結果

從圖中各種組合方式求得的標準差與參考值(組合序號為36)比較可以看出公共點組合序號為 1、7、20、25、26、28的6種組合方式求解結果精度較高，與之相對應的條件數均較小，對應的參數解算精度較高。在這6中組合方式中，組合序號為1的解算精度更高，這與利用本文提出的方法搜索到的公共點組合方式一致，因此本文提出的基于象限分布的公共點選擇方法在三維坐標轉換中能夠選出分布合理、數量少、參數求解精度高的公共點組合方式。

4 結束語

本文提出一種基于象限分布的公共點選取新方法，并結合模擬數據驗證該方法指導平面坐標轉換和空間坐標轉換時公共點布設和選取的可行性，實驗結果證明在公共點數量相同且較少的條件下，利用該方法選取公共點分布最為合理，幾何強度最高，只需少量公共點即可達到大量公共點共同求解的效果。