深海高強度鋼環肋圓柱殼單位容積重量優化設計

余 俊，歐陽呂偉，李艷青，陸 波

(中國船舶科學研究中心，江蘇 無錫 214082)

0 引 言

環肋圓柱殼是典型的深海耐壓結構，在結構設計時，在一定容積下減輕結構重量，提高結構裝載重量，是深海耐壓結構設計常常關心的問題。高強度鋼材料屈服強度、抗拉強度比普通鋼要高，在滿足同樣的結構強度、使用容積的情況下，結構設計中采用高強度鋼材料，可以減少鋼材使用量，進而減小結構的單位容積重量，故高強度鋼在深海耐壓結構中被廣泛應用。

為了減輕環肋圓柱殼重量，需要對其進行優化設計。國內外學者對環肋圓柱殼優化方法進行了廣泛的研究。Liang 等[1]提出了在穩定性和屈服強度約束條件下，受靜水壓力的潛艇耐壓殼體結構重量最輕的優化設計方案。由于該設計問題屬于離散變量多模態約束最小值問題，作者采用回溯程序設計方法進行求解，獲得的優化設計方案的重量比原有模型重量減輕6.65%。Bagheri 等[2]采用遺傳算法對環肋圓柱殼進行多目標優化設計，以最大固有頻率和最小結構重量為目標函數，采用權重法將多目標轉化為單目標，研究了權重系數、加強筋結構形式和設計變量的取值范圍對優化結果的影響。

國內丁海旭等[3]對潛艇耐壓船體進行優化設計，以結構重量和滿應力設計為目標，建立單目標非線性約束優化的目標規劃模型，求解連續與離散混合變量的最優解，并進行規整，獲得了關于滿應力設計和結構重量較輕的耐壓船體設計方案。楊卓懿等[4]對環肋圓柱殼進行了優化，建立了強度計算的響應面模型，并采用罰函數法進行優化，獲得了結構重量最輕的優化解。王燕[5]對潛艇耐壓結構優化設計方法進行探索，采用有限元法對系列潛艇環肋骨圓柱殼進行強度和穩定性分析，分別建立了分析的二次響應面模型和Kringing近似模型，然后以重量為目標，采用混合整型優化方法對環肋圓柱殼進行優化設計，并進行了對比。

目前國內外環肋圓柱殼結構優化研究均是針對具體模型的優化，主要研究優化算法和優化過程，優化結果只適用于具體的設計模型，缺少對高強度鋼材料通用性的優化成果，以指導環肋圓柱殼結構設計。本文首先建立了600 MPa級高強度鋼環肋圓柱殼結構優化計算方法。以多學科優化軟件Isight為平臺，聯合利用多島遺傳算法（MIGA）和序列二次規劃法（NLPQL）對高強度鋼環肋圓柱殼單位容積重量進行優化，得到了最小環肋圓柱殼單位容積重量、最優的半徑厚度比與最大工作壓力的關系曲線和擬合公式。

1 環肋圓柱殼無量綱化的強度穩定性計算方法

適用于600 MPa級高強度鋼環肋圓柱殼無量綱化的強度和穩定性計算方法，主要依據GJB/Z 21A-2001潛艇結構設計計算方法[6]和現代潛艇結構強度理論與試驗[7]進行計算。計算時選用以下幾個無量綱的變量、，，，，，。 其 中為 環 肋 圓柱殼耐壓殼體中面半徑；t 為耐壓殼體厚度；為T型肋骨腹板厚度；為T型肋骨腹板高度；為T型肋骨的面板寬度；為T型肋骨面板厚度；和為無量綱化的結構參數，計算公式如下：

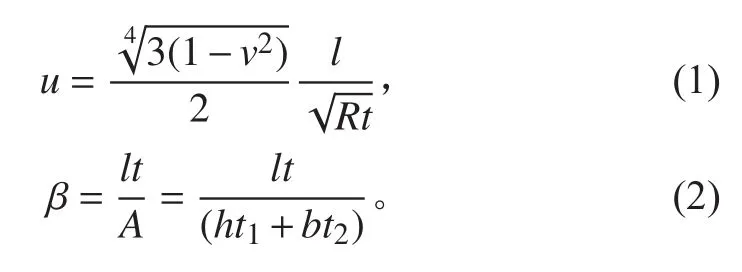
1.1 環肋圓柱殼無量綱化的強度計算方法

計算下列參數：

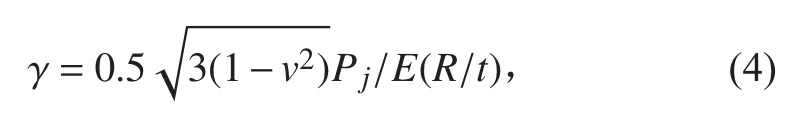
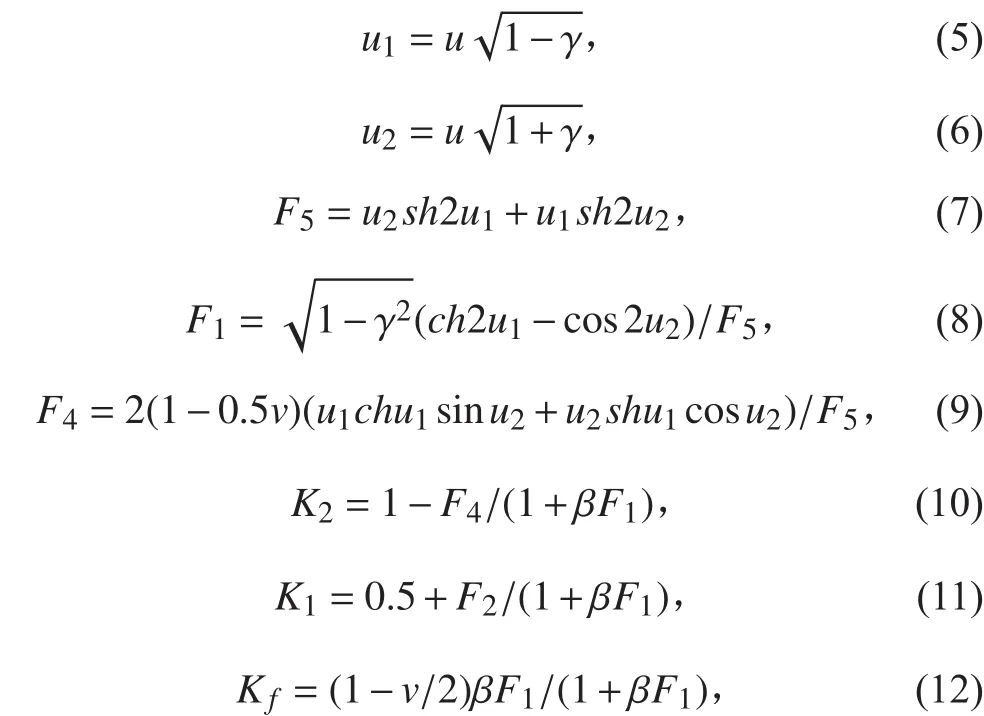
肋骨根部殼板內表面的縱向應力：

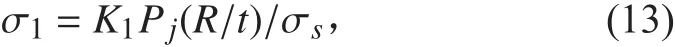
跨中殼板的中面周向應力：

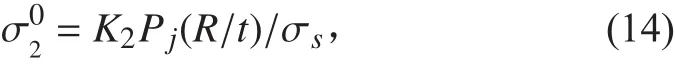
肋骨平均應力：

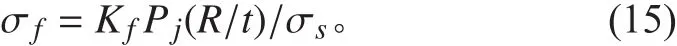
1.2 環肋圓柱殼無量綱化的穩定性計算方法

相鄰肋骨殼板歐拉失穩壓力：

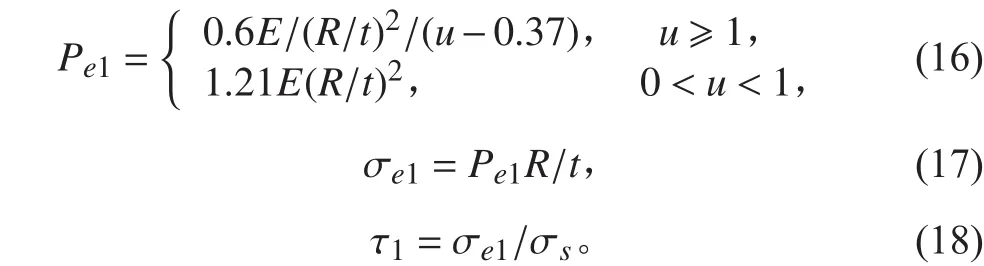
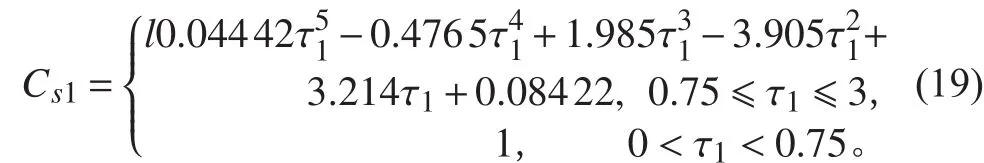
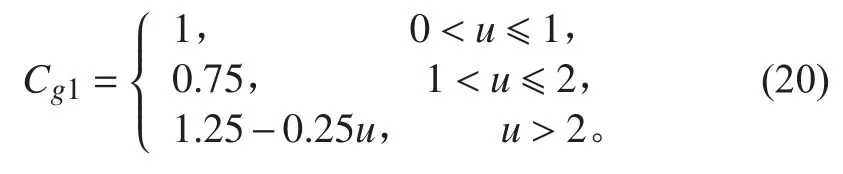
肋間殼板失穩臨界壓力：

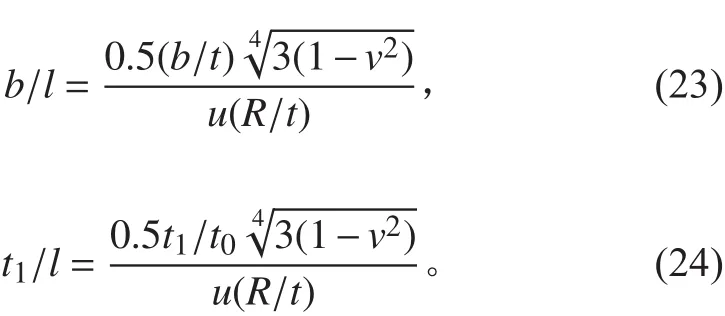
肋骨型心具體殼板表面高度與厚度之比：

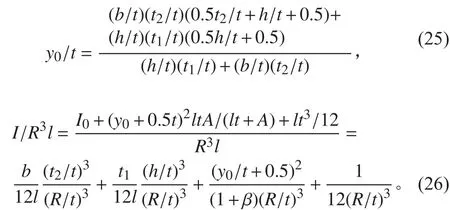
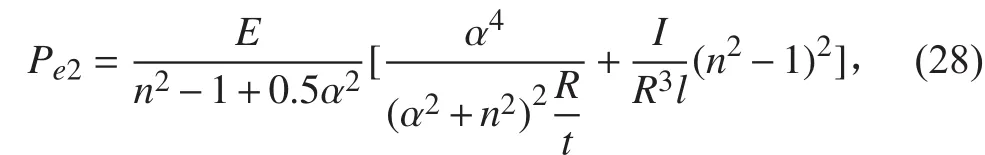
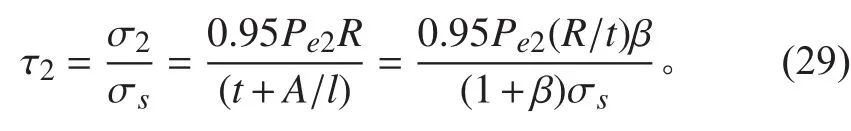
艙段間失穩臨界壓力：

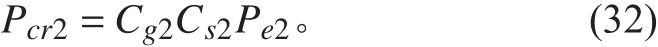
2 優化模型和優化算法

2.1 設計變量

查閱相關資料，設計變量取值范圍如下：

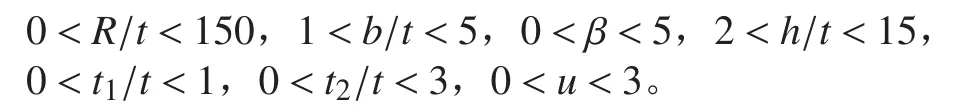
2.2 目標函數

單位容積重量為目標函數：

2.3 約束條件

1）強度約束

跨中殼板中面周向應力：

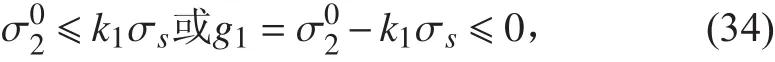
肋骨根部殼板內表面縱向應力：

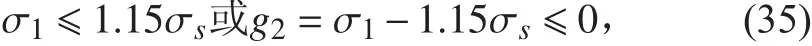
肋骨平均應力：

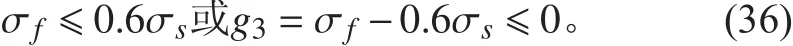
2）穩定性約束

肋間殼板失穩臨界壓力：

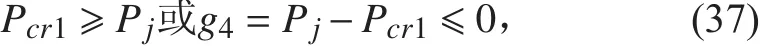
艙段總體失穩臨界壓力：

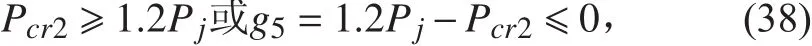
3）幾何約束

肋骨高度與殼板半徑之比：

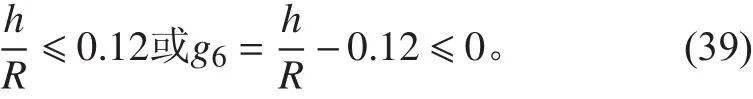
2.4 優化算法

該優化問題屬于連續型變量約束優化問題，聯合運用多島遺傳算法（MIGA）和序列二次規劃法（NLPQL）進行優化，采用多島遺傳算法進行全局搜索，得到一個最優解，然后在該最優解基礎上采用進一步局部尋優，從而得到滿足約束條件單位容積重量最輕的設計方案。

多島遺傳算法是全局優化算法的一種，它能求解全局最優解，避免了在局部區域搜索；同時它只評價設計點，不計算任何函數的梯度，適合處理離散型和連續性設計變量。相比傳統遺傳算法，它將每一代的種群劃分為幾個“島”，每個“島”都進行傳統遺傳算法操作，島與島之間有個體發生“遷移”，這使其具有更優良的全局求解能力。

序列二次規劃法（NLPQL）能夠處理設計變量實型問題。NLPQL算法將目標函數以二階泰勒級數展開，并把約束條件線性化，通過解二次規劃得到下一個設計點。該方法能夠有效地探索初始設計點周圍局部區域，如果設計空間是連續單峰的形態，能夠沿最快下降方向快速搜索。

2.5 優化過程

本文采用Isight軟件對強度和穩定性計算模型進行集成，然后在Isight軟件優化算法下進行驅動優化，圖1為Isight對環肋圓柱殼進行確定性優化的流程圖。

3 600 MPa 級高強度鋼單位容積重量優化結果

表1列出了600 MPa級高強度鋼環肋圓柱殼單位容積重量優化結果，從表1可以看出，時，在同一工作壓力下，最小單位容積重量及對應化不大。

從統計學角度，一項試驗中欲考察的變量稱為因子或因素，因子被考察的范圍稱為試驗范圍，試驗結果稱為響應（Response）或輸出（Output），在試驗范圍內，因素所取的值稱為水平。常用的試驗設計方法有全因子設計、正交設計、中心組合設計、拉丁方設計和最優拉丁方設計等。對于因子數目較大時，可以采用拉丁方設計或最優拉丁方設計[8]，拉丁方設計中每個因子的設計空間等分份，然后每個因子水平隨機組合共確定個采樣點（一個因子每個水平只研究一次）。而最優拉丁方法是在拉丁方法基礎上，對每個因子組合方式進行優化，使設計點在設計空間均勻分布，如圖2所示。

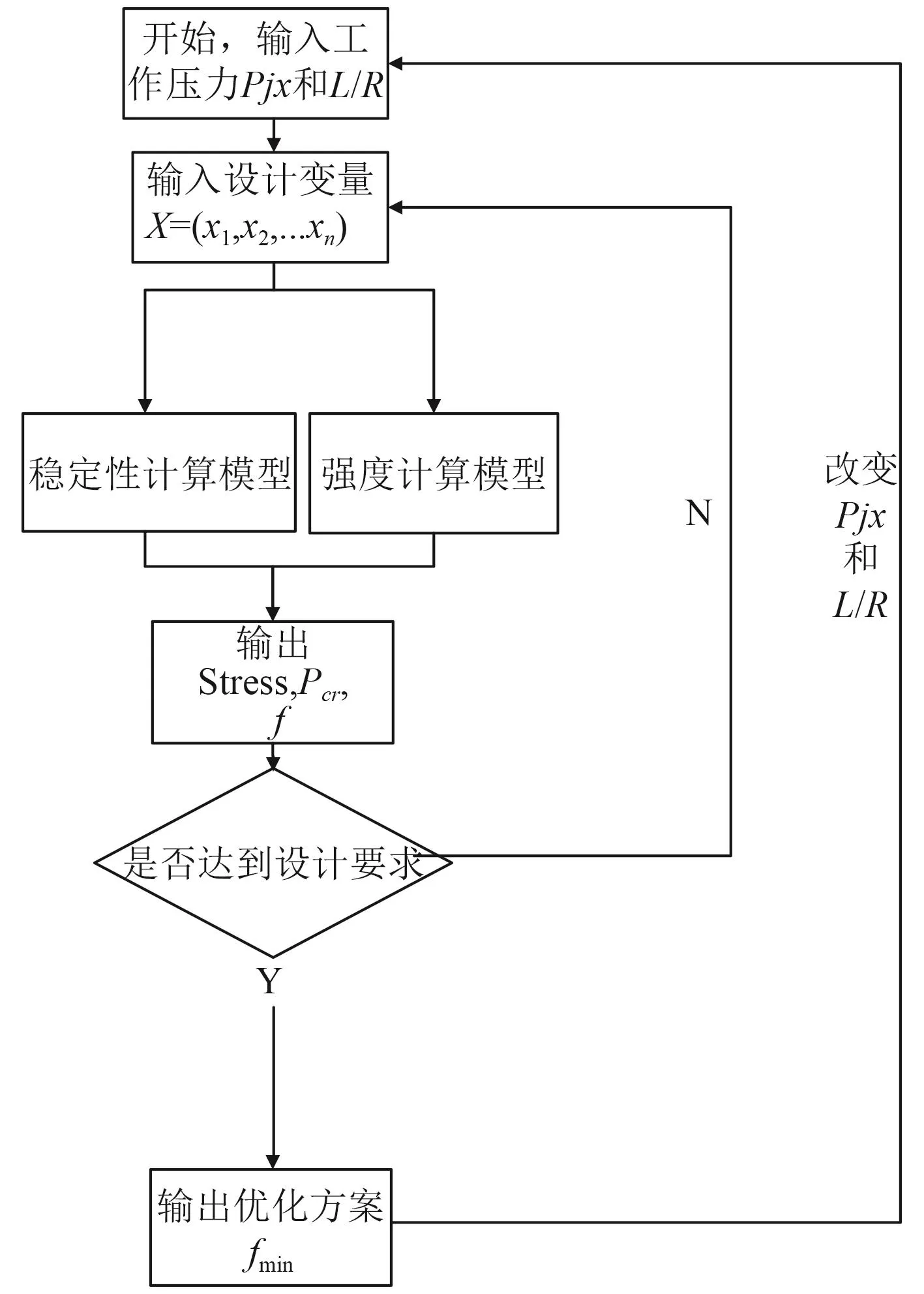
圖1 環肋圓柱殼確定性優化流程圖Fig.1 Deterministic optimization process of ring-stiffened cylindrical shell

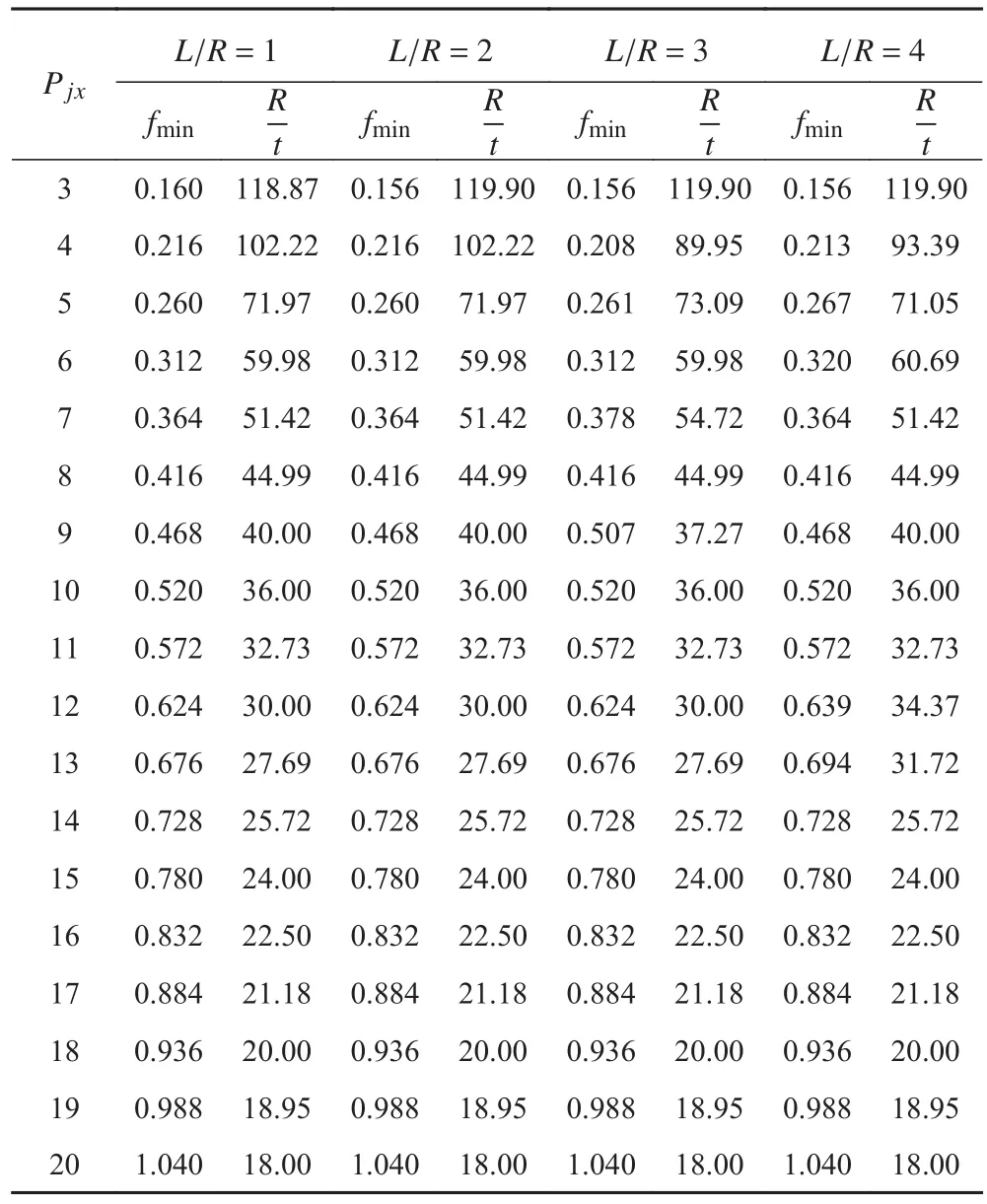
表1 600 MPa級高強度鋼環肋圓柱殼單位容積重量優化結果Tab.1 Weight to Volume Optimization results of the 600 MPa ring-stiffened cylindrical high-strength steel shell

本文采用最優拉丁方進行試驗設計，取500個取樣點，對每個采樣點進行單位容積重量計算，然后進行各變量之間的相關性分析，得到單位容積重量和自變量的復相關系數，如圖3所示。（）與自變量的復相關系數圖如圖4所示，與自變量的復相關系數圖如圖5所示，與自變量的復相關系數圖如圖6所示。圖中縱坐標為因變量相關系數，橫坐標為自變量。

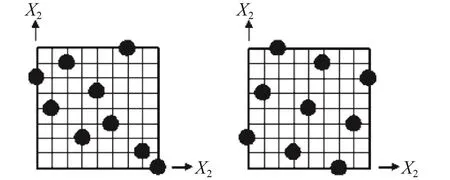
圖2 拉丁方設計（左）和最優拉丁方設計（右）Fig.2 Latin square design (left) and optimal Latin square design (right)

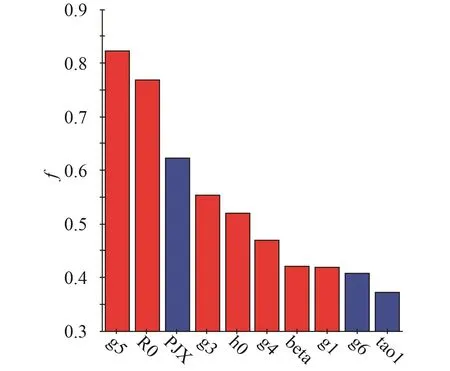
圖3 與自變量的復相關系數Fig.3 Multiple correlation coefficient between and independent variable

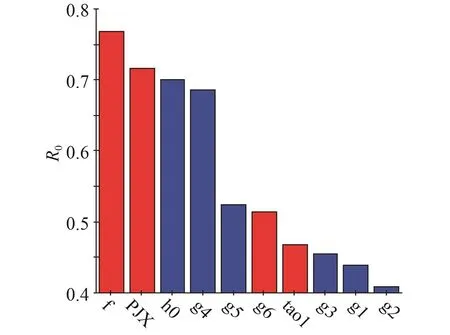
圖4 （）與自變量復相關系數Fig.4 Multiple correlation coefficient between ( ) and independent variable

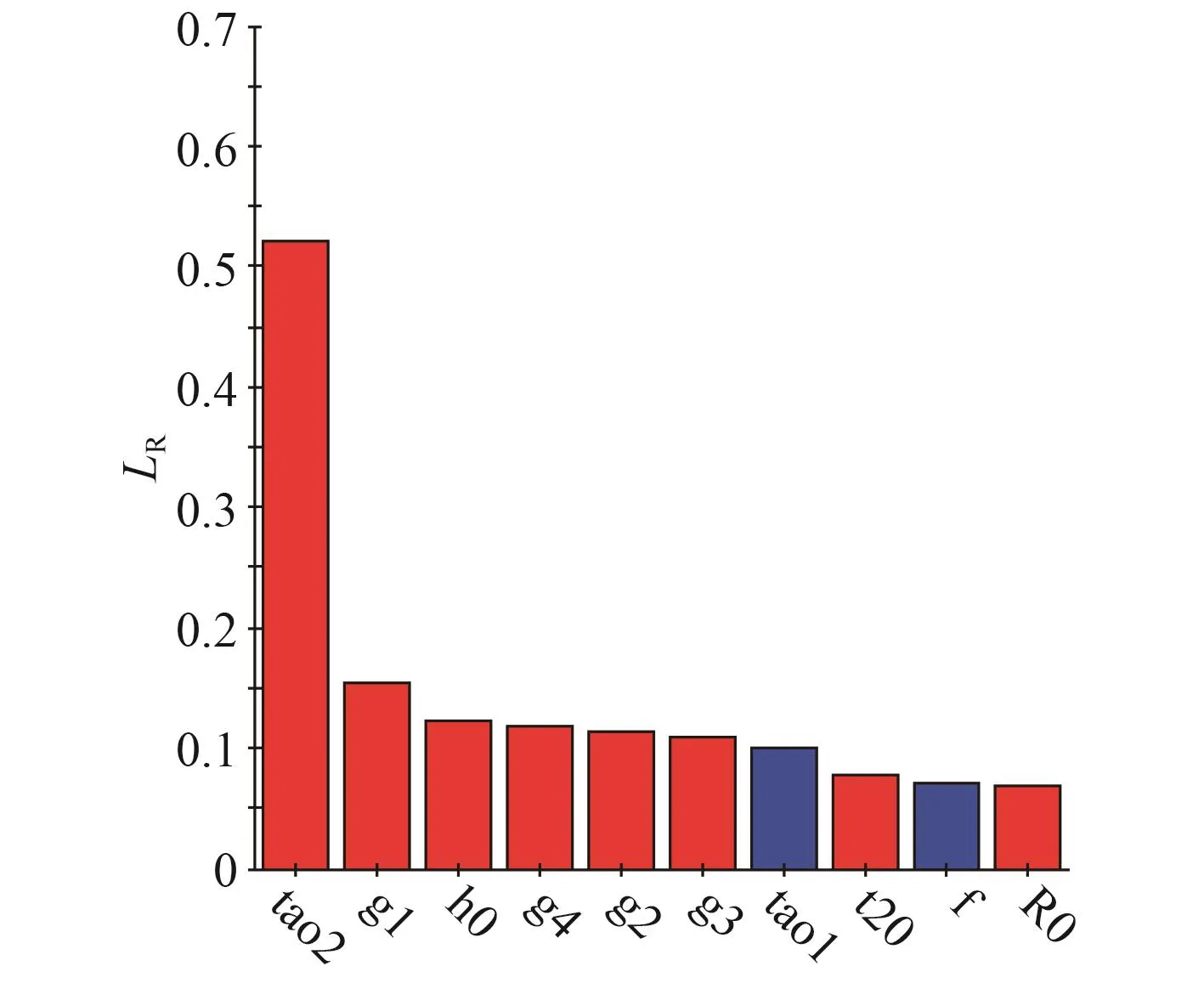
圖5 與 自變量復相關系數Fig.5 Multiple correlation coefficient between and independent variable

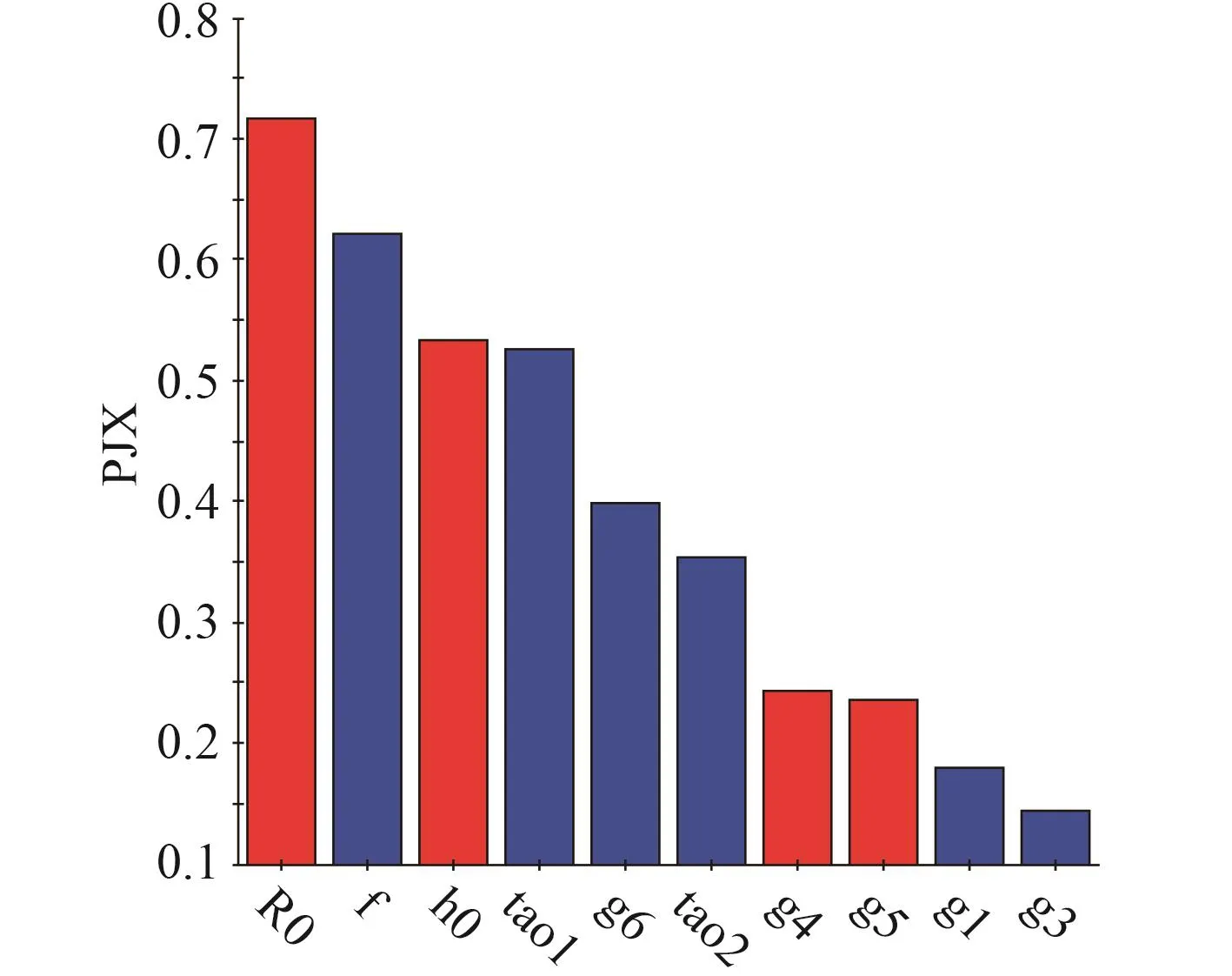
圖6 與自變量復相關系數Fig.6 Multiple correlation coefficient between and independent variable

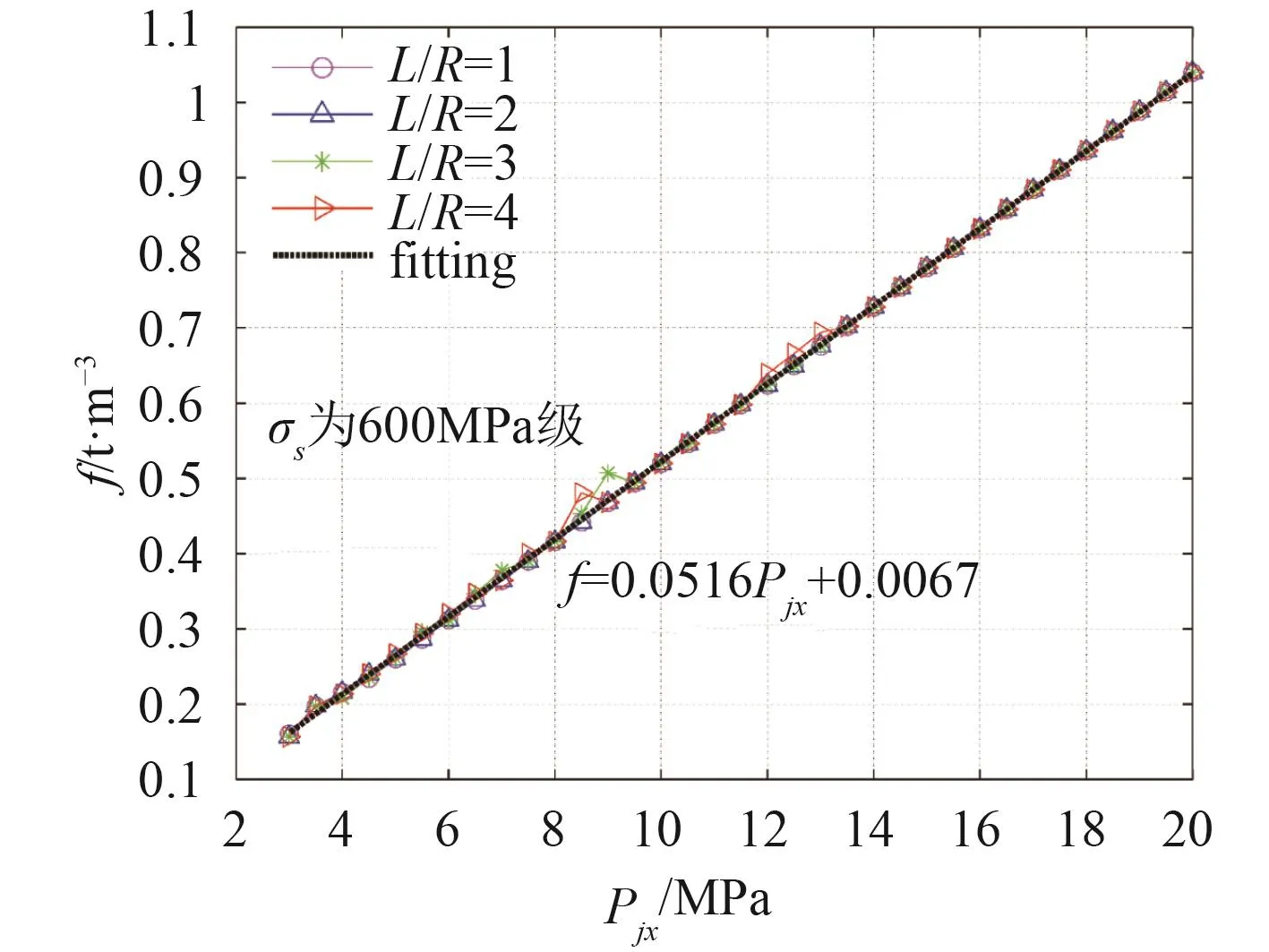
圖7 600 MPa 級高強度鋼環肋圓柱殼與關系Fig.7 Relation between and of the 600 MPa ring-stiffened cylindrical high-strength steel shell

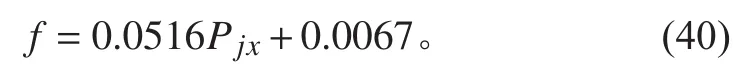
與1接近，說明擬合精度較高，該公式可以用于600 MPa高強度鋼環肋圓柱殼最小的單位容積重量計算。

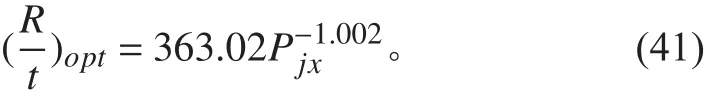
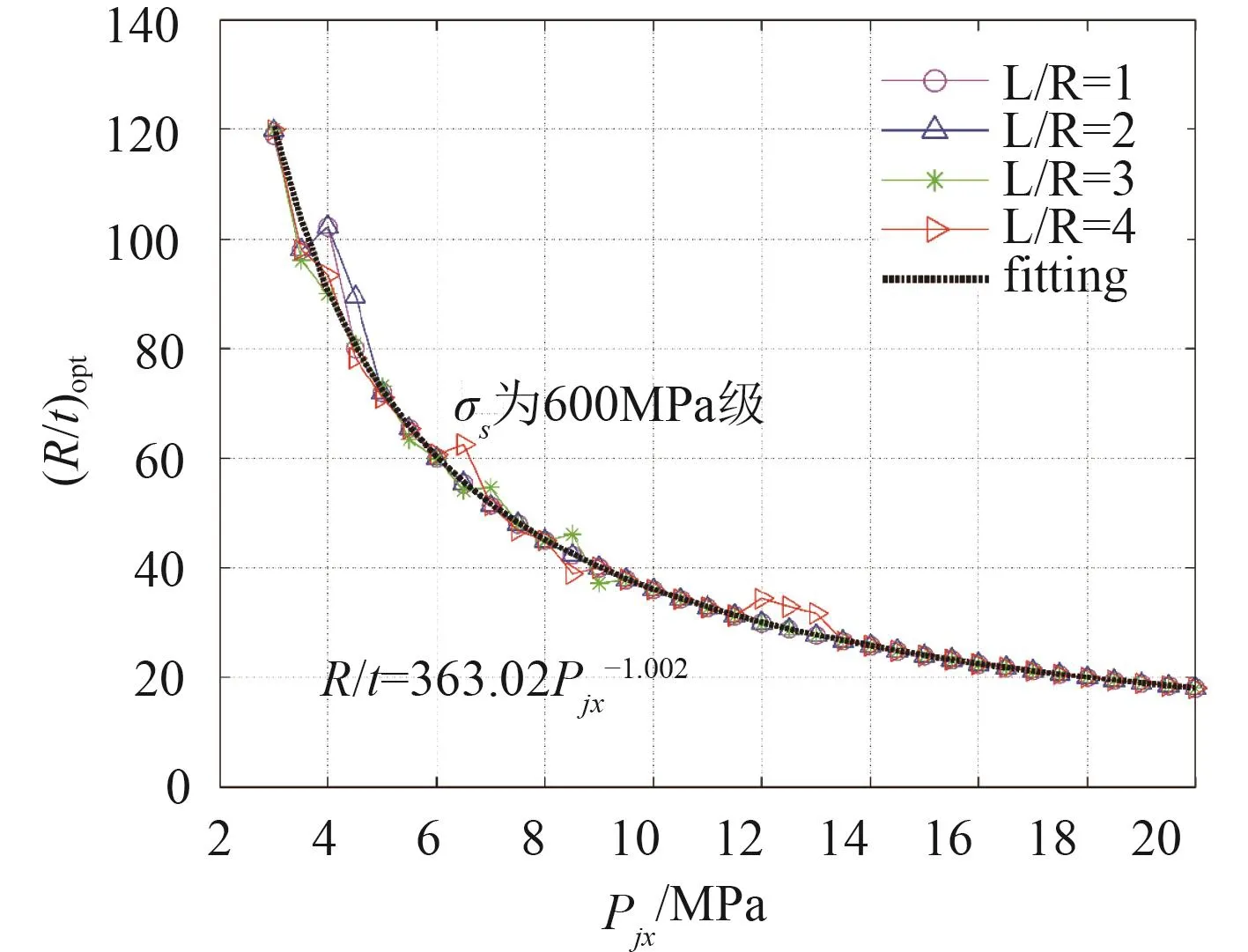
圖8 600 MPa級高強度鋼環肋圓柱殼Fig.8 Relation betweenan of the 600 MPa ringstiffened cylindrical high-strength steel shell

4 結 語

1）本文依據GJB/Z 21A-2001潛艇結構設計計算方法建立了600 MPa級高強度鋼環肋圓柱殼強度和穩定性無量綱的計算方法，該方法可用于環肋圓柱殼強度和穩定性校核和優化設計。

2）在上述計算方法的基礎上對環肋圓柱殼單位體積重量進行優化，通過多島遺傳算法（MIGA）整體尋優和序列二次規劃法（NLPQL）局部尋優，得到了在不同的圓柱殼長度半徑比、不同的最大工作壓力下，600 MPa級高強度鋼環肋圓柱殼最小的單位容積重量和對應的最優的半徑厚度比，在圓柱殼長度半徑比為1，2，3，4情況下分別繪制了600 MPa級、高強度環肋圓柱殼最大工作壓力與最小的單位容積重量關系曲線，最大工作壓力與最優的半徑厚度比關系曲線，并證明了最小的單位容積重量、最優的半徑厚度比僅和材料、最大工作壓力有關，和圓柱殼長度半徑比關系不大。

3）根據上述優化結果，提出了計算600 MPa級高強度環肋圓柱殼最小的單位容積重量、最優的半徑厚度比的擬合公式，該公式可以用于評估高強度鋼環肋圓柱殼單位容積重量是否最優，可以計算單位容積重量最優情況下的半徑厚度比，指導深海耐壓環肋圓柱殼優化設計與評估。