一種大規模水下聲傳感器網絡定位技術

王連文，姚 曜，杜紅松，王 涵

(1. 中國人民解放軍92942部隊，北京 100161；2. 中國人民解放軍91977部隊，北京 100036)

0 引 言

水下聲學傳感器網絡是新興的海洋技術熱點，通過在目標水域大量布放傳感器節點，以水聲無線通信方式形成的一個多跳的自組織網絡系統，協作地感知、采集和處理網絡覆蓋區域中的信息，并發送給接收者[1]。主要應用于海洋環境監測、海洋資源開發、災難預防，輔助導航、戰術監視、水雷偵察等方面[2]。

大規模水下聲傳感器網絡通常用于監測部署區域的各種環境參數，比如溫度，鹽度等，而這些信息只有在與網絡中的節點的位置綁定時才是有意義的[1]。此外，在有效利用節點能源、提高網絡的吞吐量等方面，基于位置信息的地理路由算法比單純的廣播方法往往更有效，相當數量的MAC協議也需要節點的位置信息。因此大范圍水下聲傳感器網絡中的精確定位技術是一個亟待研究的關鍵技術。

目前的水下聲傳感器網絡定位方法主要分為兩大類：基于測距的定位方法和不基于測距定位算法[3]。基于測距的定位算法，節點首先測量到錨節點之間的距離和角度，然后利用三邊測量法或三角測量法進行目標的定位解算，測距方式主要有RSSI，TOA，TDOA，角度測量主要有AOA等。不基于測距的定位方法，主要包括質心定位算法（Centroid scheme）、DV-hop定位算法、APIT定位算法、ALS定位算法、Amorphous定位算法等。基于測距的定位算法具有較高的精度，但精確測距需要額外的硬件裝置支持，有些測距方法依賴精確的時間同步。不基于測距的定位算法普遍定位精度不高，應用面有限，需要較大的通信消耗。在水下傳感器網絡中，總體來說基于距離測量的、有精度能力保障的定位技術是研究與應用的主流。

文獻[4]中，作者提出了一種水下GPS系統，用可以與衛星通信得到自己的精確位置的水面浮標充當水下的GPS衛星節點，為浮標通信范圍內的節點提供位置信息，供其進行定位解算，但是這種方法需要時間同步，且只適用于單跳網絡。文獻[5]提出了一種基于無線傳感器網絡的水下定位系統，使用大量的裝有水聽器和GPS的標準站，采用聲功率水平測距，利用發送和接受的電壓差來計算距離，提出了新的方法，但是該方法是接收信號強度指示（RSSI）的水聲測距應用，定位精度一般。文獻[6]中，針對在稀疏網絡中三維定位的問題，設計了USP分布式定位框架，將3D定位問題通過平面投影技術轉化成對應的2D問題，通過迭代改善精度，有更低的數據存儲量和更低的數據計算要求，但該方法由于網絡中采用的錨節點數量很少，在稀疏網絡中網絡定位覆蓋率較低，網絡定位時間長。文獻[7]中，作者提出了一種AUV輔助的水下傳感器網絡定位方法，AUV上浮到海面時接收GPS信號，然后以設定的軌跡下降到特定的深度，在巡航過程中喚醒節點，節點利用請求/應答的方式進行測距，實現自己的定位解算，但是AUV是非常昂貴的。而且這些方法都是適用于小規模水下聲傳感器網絡定位的技術，對于大規模聲傳感器網絡并不適用。

迭代定位算法首先由Joe Albowicz等提出并應用于密集的無線電傳感器網絡[8]，作者提出了一種位置傳播算法，在密集網絡中布放少量的錨節點，提出了一種基于殘差的定位精度評價方法評價成功定位的普通節點的定位精度，將精度高的節點升級為錨節點，從而使得系統的定位覆蓋率迭代地增加，實現了大范圍傳感器網絡較高的定位覆蓋率和較小的定位誤差。

本文研究水下傳感器網絡中的迭代定位方法，研究了節點定位過程中錨節點共線度的選取方式，并將一種新的三維歐幾里得距離估計方法應用到網絡中研究了普通的定位方法、三維歐幾里得方法、迭代定位方法、聯合三維歐幾里得距離估計的迭代方法的定位覆蓋率和定位誤差。

1 迭代定位機制

1.1 網絡結構

迭代定位的原理如圖1所示，節點部署在三維水下區域中，共有水面浮標、錨節點和普通節點3種。

其中，水面浮標部署在水面，可以通過與GPS衛星或地面站進行無線電通信獲得自己的精確位置供錨節點進行精確的位置解算。錨節點是水下節點中一類數量較少但是通信能力較強的節點，它與水面浮標進行通信可以獲得自身的精確位置，并廣播自己的位置信息供通信范圍內的普通節點進行定位解算。普通節點主要通過與自己周圍的鄰居錨節點通信進行測距和自身的位置解算。

1.2 定位步驟

水下聲傳感器網絡中迭代定位方法主要分成4個階段：

1）錨節點獲得自身位置并泛洪廣播定位信息的階段

錨節點在定位過程中周期性與水面浮標進行通信，當節點接收到4個以上滿足條件的浮標的位置和距離信息之后，進行自身定位解算，并泛洪廣播定位信息（包含錨節點的ID，時間戳和節點坐標）。

2）普通節點定位解算的階段

普通節點周期性發送信標信息（包含自己的節點ID和時間戳）供鄰居節點進行測距，并且接收鄰居節點的信標信息對鄰居節點進行測距并在鄰居節點鏈表中保存鄰居節點的節點ID和距離信息，同時節點接收錨節點的定位信息，并在錨節點信息鏈表中添加得到的錨節點的節點ID，距離，坐標。當普通節點接收到滿足條件的4個以上錨節點的定位信息之后就可以利用球面交匯的方法進行定位解算。球面交匯定位解算的基本方程如下：

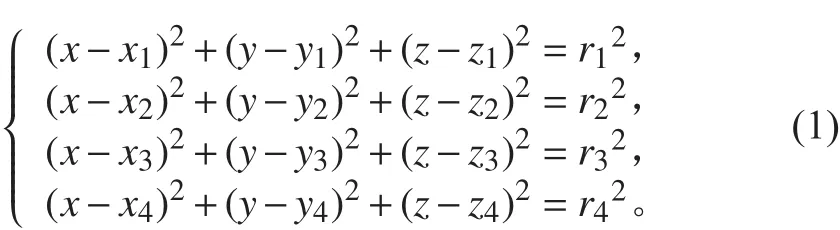
經過降次處理，得到三元一次方程組：

3）普通節點定位結果自評價階段

迭代定位算法，普通節點位置估計成功之后，利用已估計的位置信息和測距信息利用式（3）計算置信值[9]，評價自己的定位結果。

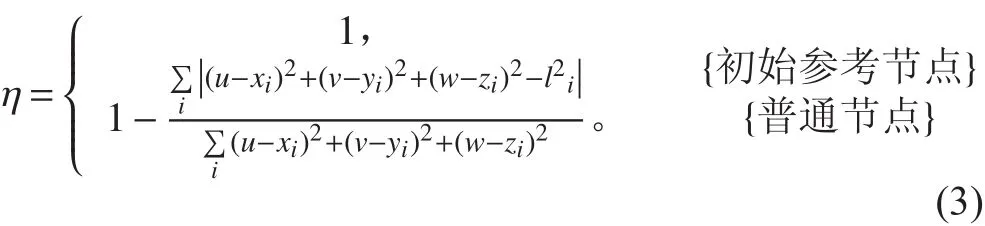
4）迭代定位階段

普通節點計算置信值之后，如果置信值大于提前設定的門限，則該普通節點升級為錨節點，廣播自己的定位信息供其他鄰居普通節點進行位置解算。隨著定位過程的進行，將會有越來越多的普通節點通過評價定位質量的機制升級為錨節點，這樣節點部署區域的定位覆蓋率就會迭代地增加。

1.3 迭代算法流程

2 三維歐幾里得算法

2.1 算法描述

在三維無線傳感器網絡空間中，未知節點只要獲得至少4個錨節點的位置信息便可以應用三維最小二乘定位算法來實現其定位。但當未知節點通信范圍內錨節點數目少于4個時，未知節點將無法定位[10]。Euclidean定位算法是由美國路特葛斯大學（Rutgers University）的Niculescu等提出的，它的定位是利用已知平面幾何原理來估測與錨節點距離兩跳的未知節點的所在位置。文獻[9]中將二維歐幾里得距離估計擴展到了三維。當錨節點數量不足時，普通節點可以通過三維歐幾里得距離估計計算到一跳范圍之外的錨節點距離信息。這樣，待定位節點可以利用一跳范圍之外的錨節點參與定位解算，增加定位成功率。

圖2 迭代算法流程圖Fig.2 The flow chart of iterative algorithm

基本原理如圖3所示，待定位節點E和參考節A的不相鄰，并且有2個鄰居錨節點BC，節點E想要計算到節點A的距離，如果存在D點使得節點E已知節點對AB，AC，AD，BD，BC，CD，EB，EC，ED之間的距離信息，則節點E利用ABC基本平面解算兩個D位置，再利用BCD求解出4個E的位置，再找一個與D相異的W點求出另外4個E的位置，即可篩選出E的位置求出AE距離。

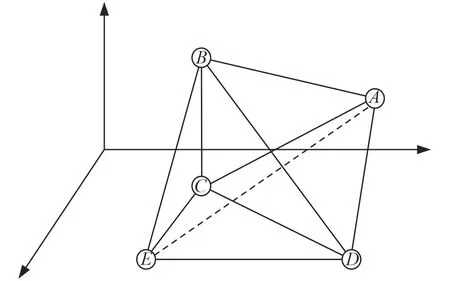
圖3 三維歐幾里得距離估計示意圖Fig.3 The schematic figure of 3D Euclidean distance estimation

文獻[11]提出了一種利用坐標法解決三維歐幾里得距離估計的問題，大大減小了算法的計算量，對算法中BCD平面的錨節點沒有數量要求，是解決三維歐幾里得距離估計的一種較好的方法。其原理如圖4所示。

利用BC為x軸與BC垂直的軸為y軸，與BCD所在平面垂直的軸為z軸，建立坐標系，可利用方程（4）求得D點的坐標

圖4 相對坐標法三維歐幾里得距離估計原理圖Fig.4 The schematic diagram of 3D Euclidean distance estimation in

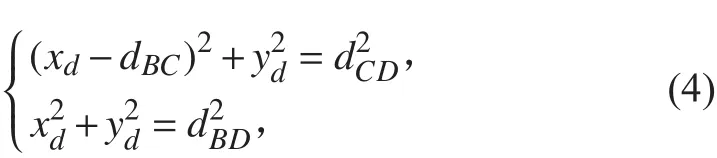
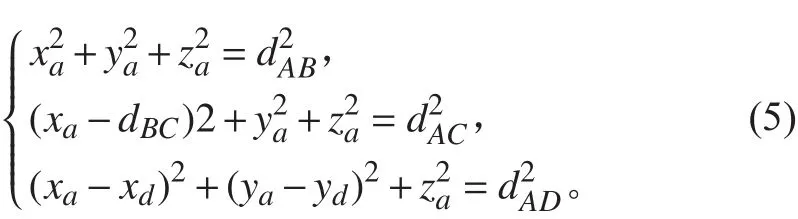
2.2 算法流程

算法流程如圖5所示。

圖5 3DEculidean 算法流程Fig.5 The flow of 3D Euclidean algorithm

3 仿真結果

本文的仿真過程中，節點布放在 20 km×20 km×4 km的區域中。節點的通信距離為2 km。距離測量值符合均值為真值，標準差為1 m的正態分布。節點數量從以步長值為50，從500到900變化，錨節點占20%。普通節點升級為錨節點的置信值為0.98。每個節點密度（節點數量對應）運行100次，每次運行所有節點進行5次迭代。

3.1 節點部署情況

圖6代表仿真區域中有500個節點，錨節點占20%的情況下一次運行所產生的節點部署情況示意圖。

圖6 傳感器節點分布圖示例Fig.6 Example of sensor node distribution diagram

3.2 節點密度與節點數量關系

節點密度定義為區域中當前節點數量下每個節點通信范圍內的平均節點數量。在部署區域中網絡中的節點數量與節點密度的關系如圖7所示。

圖7 節點密度與節點數量關系Fig.7 The relationship between node density and number of node

3.3 不共線方式的選取

由于節點定位過程中節點共線會導致較大誤差，所以在定位解算過程中需要避免3個節點或者4個節點共線的情況。

用于解算的錨節點每3個組成1個組合，共線度的定義為任意3個錨節點組成的三角形內角余弦值的最大值。圖7仿真了節點位置為[0,0,0]，錨節點位置為，測距信息服從真值為均值，標準差為1 m的正態分布時錨節點共線度與定位誤差的關系圖。從圖8中可以看出隨著角度值的變小，當節點最小角度余弦值小于0.99（對應角度為8°）時，節點定位精度變化不大，但是當最小角度余弦值大于0.99時節點的定位誤差急劇增大，造成很高的定位誤差。本文迭代定位過程中選取不共線條件是任意3個節點組合三角形內角最小角度余弦值不大于0.95（對應角度為18.2°）。

圖8 最大余弦值與定位誤差關系圖Fig.8 Relation diagram of maximum cosine value and positioning error

3.4 定位覆蓋率

定位覆蓋率定義為：定位過程結束后所有節點中已知位置的節點數量與總節點數量的比值。此處普通定位方法指節點僅用1跳范圍內的錨節點進行定位，不進行評價升級的定位方法。圖9中可以看出，普通的定位方法定位覆蓋率很低，而單純的三維歐幾里得方法對普通定位方法的結果有所改善但是效果并不明顯。這是由于節點密度較低，錨節點數量較少時，節點兩跳范圍內的錨節點數量也較少，即使應用3DEculidean方法節點也較難找到足夠數量的錨節點，導致定位覆蓋率改善不大，隨著節點密度的升高定位結果有所改善。迭代定位方法的定位覆蓋率要明顯高于前兩者，是因為隨著迭代過程的進行，錨節點數目迭代地增加，導致系統定位覆蓋率迭代地升高。帶三維歐幾里得距離估計方法的迭代定算法的定位覆蓋率要比單純的迭代算法的定位覆蓋率高，是因為節點在運行過程中在參解算的錨節點數目不足時，會尋找一跳范圍以外的錨節點參與定位解算，隨著節點數量增加，節點密度升高，大部分節點只通過迭代作用就能找到足夠的錨節點進行定位解算，三維歐幾里得的作用將降低。

圖9 節點數量與定位覆蓋率關系圖Fig.9 Relation diagram of node number and location coverage

3.5 定位誤差

定位誤差定義為所有節點的平均定位誤差與通信距離的比值。

從圖10中可以看出，常規定位方法的定位精度最高，三維歐幾里得方法定位誤差高于常規方法，這是因為三維歐幾里是基于測距信息進行AE距離計算，其中計算節點D相對位置，計算節點A相對位置，計算節點E的相對位置，各個步驟都有誤差，由于誤差積累，最后的距離值比真實測距的誤差高，所以三維歐幾里得方法的定位誤差高于常規方法。迭代方法中由于有的錨節點是普通節點升級而來，本身就存在定位誤差，隨著迭代的進行會產生誤差的積累，導致平均定位誤差最高。聯合三維歐幾里得距離估計的迭代方法的定位誤差最高，一方面是待定位節點找到的兩跳范圍內的錨節點可能是普通節點升級之后的錨節點本身具有一定誤差，另一方面是由于之前提到的三維歐幾里得算法的誤差積累導致距離估計誤差較大。

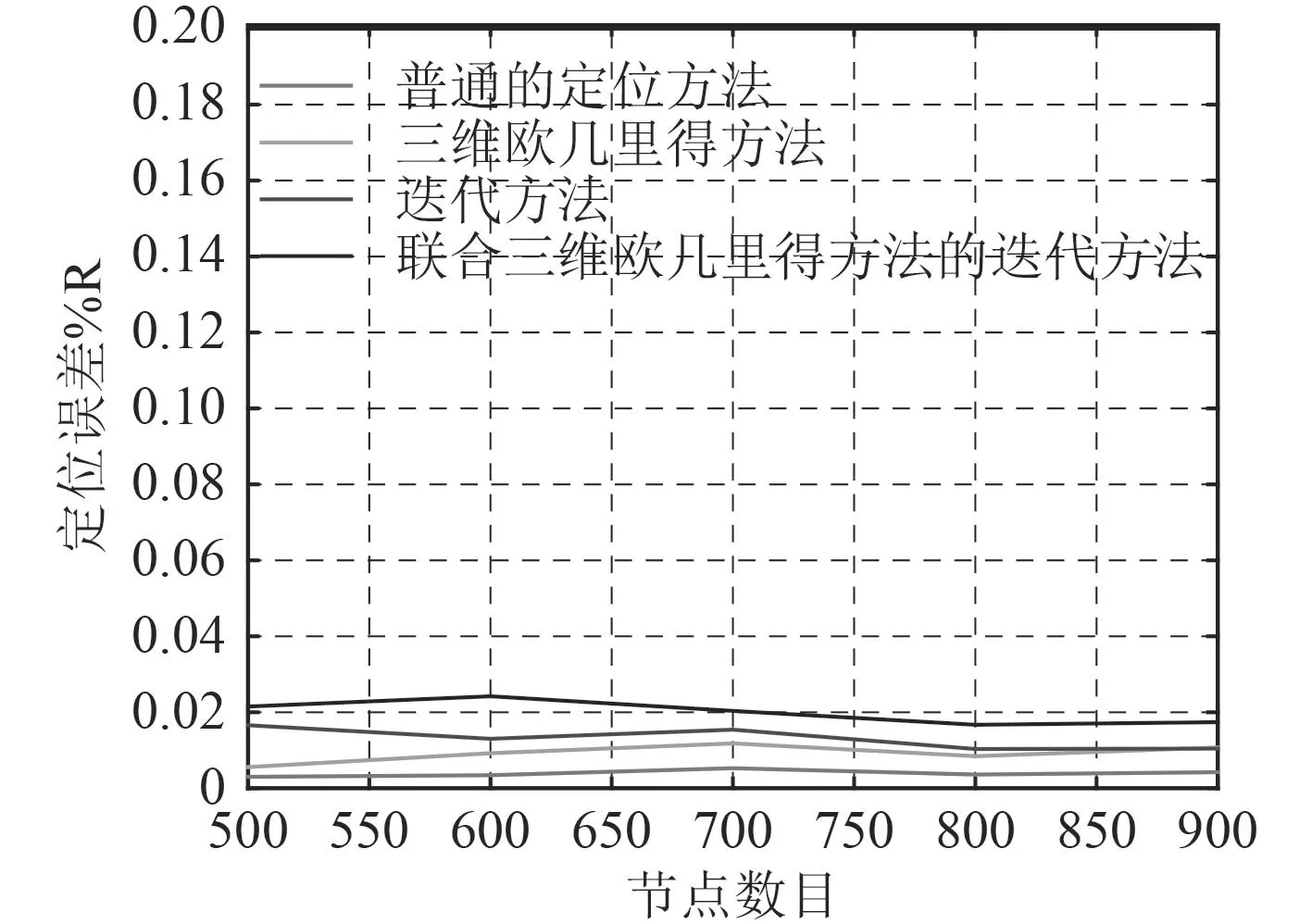
圖10 節點數量與定位誤差關系圖Fig.10 Relation diagram of node number and positioning error

4 結 語

本文研究了大規模水下傳感器網絡中的迭代定位方法，通過少量初始錨節點定位普通節點，評估定位

成功節點的精度保持情況，升級定位精度高的普通節點為錨節點參與定位余下的普通節點，使網絡的定位覆蓋率迭代地升高。利用一種相對坐標三維歐幾里得距離估計方法去估計1跳范圍外的錨節點，提高定位成功率。給出了網絡定位中節點不共線的選擇方法，比較了普通定位方法，單純的三維歐幾里得方法、迭代定位方法，聯合三維歐幾里得的迭代定位方法的定位誤差和定位覆蓋率。結果表明，以一定的精度損失為代價，迭代定位方法顯著提高了定位覆蓋率，而聯合三維歐幾里得距離估計的迭代方法可進一步提升定位覆蓋率。