不確定理論下帶懲罰機制的城市污水處理期望收益模型

張 林,李存林,2*,李 丹 (.北方民族大學數學與信息科學學院,寧夏 銀川 75002；2.北方民族大學管理學院,寧夏 銀川 75002)

隨著我國城市化率和生活水平的提高,城市產生的污水越來越多.此前,我國主要靠政府建設污水處理廠處理污水.現在,政府對污水處理都進行了市場化管理,外包(BOT)給專業企業[1].這使得政府和污水處理企業形成了委托代理關系,隨之也帶來了“道德風險”問題:政府無法準確評估企業實際的污水處理量,造成雙方信息不對稱.這種不對稱可能引發企業的投機行為,即:為了追求利潤最大化,企業不顧污水處理過程中,不確定性因素對實際污水處理量的影響,惡意提高簽約量,使簽約量大于實際處理量,來獲取更多利潤.這可能造成大量污水得不到及時處理,甚至導致城市環境污染或城市環境公共危機事件.由此造成環境和社會利益負的外部性,政府還可能為此埋單.為了降低委托代理關系中的道德風險,維護政府和社會公共利益,預防污水處理企業惡意提高簽約量的投機行為,政府必須在與企業簽訂外包合同時[2-3],引入懲罰機制降低道德風險.引入懲罰機制,致使企業充分、合理地評估生產中可能存在的不確定因素,客觀、科學地確定簽約量.

國內外學者對城市污水處理的研究主要分為兩類.一類研究污水處理的生物化學方法及工藝流程.如:污泥對水中硫化物的吸附特性[4]、冬季硝化強化與微生物種群分析[5]、污水地下滲濾系統強化脫氮試驗的研究、化學強化、污染物分析、城市廢水指標[6-8]等方面;另一類研究污水處理過程的優化與管理.如排污權價格對污水處理投資決策的影響[9]、污水處理系統最優控制[10]、企業運營成本的污水處理費制度[11]、城鎮污水處理設施空間優化配置[12-13]等.第二類研究在涉及污水處理量時,都將其刻畫為一個確定的數值.事實上,污水處理實踐中常常遇到一些復雜的、主觀的和不確定的因素[14],如管理不善、工人操作失誤、設備故障、天氣情況等,影響企業實際完成的污水處理量.因此,許多學者將企業實際污水處理量刻畫為隨機變量[15-19].眾所周知,隨機變量依賴于事件的可重復性.現實中,很多企業無法收集到足以估計其處理量的歷史數據,也無法找到其統計規律.企業只能讓同行專家利用經驗判斷或不完全的數據做出粗略估計[20].從另外角度看,之前專家對污水處理問題的研究,都聚焦在企業內部處理方式的優化或處理技術的更新.沒有學者從政府與企業關系角度研究污水處理問題.

針對以上不足,本文從以下兩個方面進行改進:一是引入公理化的不確定決策空間,將企業污水處理量刻畫為不確定空間中的不確定變量.這種不確定變量,不依賴于歷史統計數據,只依賴于專家對污水處理企業的經驗評估.這種經驗評估是建立在公理化不確定系統上,使得這種處理方式更科學,更合理;二是從政府和企業的關系角度,在污水處理的模型中引入懲罰機制,抑制企業決策中的“道德風險”.

1 研究方法

現實中,企業處理污水量受眾多因素的影響,每次影響正常生產的原因也不盡相同.這些影響生產的不確定因素,通常也是無規律可尋.一方面,如果污水處理企業有很多條生產線,企業可以在不同的生產線同時收集數據,很容易收集到估計產量分布規律的統計數據.而實踐中,污水處理企業只有一兩條相同的生產線,不具備同時收集污水處理量統計數據的條件,統計數據的收集只能一年一年積累,要收集到足以估計其產量概率分布的大樣本,需要幾年的時間,這對實際生產幾乎沒有指導意義.另一方面,隨著居民生活水平的變化,污水成分也發生變化,處理技術也在更新,整個企業生產條件發生變化,造成之前收集的數據和現在的數據不具備同分布的性質.這種背景下,用概率變量估計污水處理量顯然是不科學的,也不可行.當然,也有學者利用專家經驗進行估計,用主觀概率刻畫污水處理企業的實際處理量,然后用概率理論進行處理.這些學者忽略了專家的經驗估計相對于統計數據是較為粗略的.主觀概率又是建立在概率理論可加測度上的理論,將這種粗略的經驗估計變量用在具有可加性的概率測度上,意味著人為將專家粗略估計的變量假定為一個相對精確的統計變量.這使得專家的經驗估計在運算中具有了可加性.而理論上沒有人證明主觀經驗具有可加性,實踐中也不可能有人相信一個主觀的經驗判斷還具有可加性.這種用概率理論或主觀概率理論處理專家主觀經驗數據,必然造成企業對自己實際污水處理量估計的過度自信,導致企業簽約量大于實際處理量.在具有懲罰機制的條件下,企業觸發懲罰條款的可能性大增,收益也會受損.若由于樂觀估計造成的過多簽約污水,得不到及時處理,還可能導致環境危機事件.

本文引入 Liu[20-21]提出的公理化不確定理論.這種理論中的不確定變量,不依賴于事件的可重復性,只依賴于行業專家對實際狀況的經驗評估,這種經驗評估不但是建立在非可加測度基礎上的,而且是建立在公理化系統上的.這有效的避免了主觀概率系統中,主觀經驗估計具有可加性的弱點.

定義1[20]設Γ是一個非空集,l是Γ上的一個σ?代數,l上的元素Λ稱為事件,M{Λ}是事件Λ發生的信度. Λc是Λ在l上的補集.若以下三個公理

公理1. (規范性公理) 對于全集Γ,有M{Λ}=1.

公理 2. (對偶性公理) 對于任意事件Λ,有M{Λ}+M{Λc}=1.

公理3. (次可加性公理)對于事件Λ1, Λ2,??,Λn,???,有則稱M為一個不確定測度,稱三元集(Γ,l,M)為一個不確定空間.

定義 2[20]設ξ是一個不確定變量,則Φ(x) = M { ξ ≤x}是ξ的分布函數,其中x∈?.

定理 1[20]設ξ是一個具有不確定分布Φ的不確定變量,若它的期望值存在,則期望值為

定義3 一個不確定變量ξ滿足

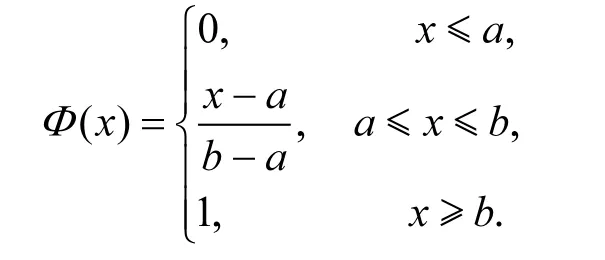
則稱ξ是線性的,且服從線性不確定分布,記為ξ ～ L[a,b].

定理 2[22]設ξ是一個具有不確定分布Φ的不確定變量,若 f(x)是一個嚴格單調(單增或單減)函數,則存在期望值

2 模型的建立與求解

如引言所述,政府在與污水處理企業簽訂委托代理合同時,應增加懲罰條款,以遏制企業“道德風險”.模型中政府對污水處理企業的懲罰機制設計為:對未完成的污水量,按照合約價乘以一定的懲罰率實施懲罰.

2.1 模型假設

(1)假定企業實際污水處理量為不確定空間的不確定變量.

(2)假設政府能提供給企業足夠的污水量,若污水供給量不足,政府應按簽約量支付費用;

(3)對企業的懲罰只針對簽約量中未完成部分,對完成部分按照合同計價;

(4)一切不可抗力因素導致的不良后果,由政府和企業雙方共同承擔,不影響簽約效果.

現在給出模型中使用的符號說明

x企業與政府簽約的污水量(萬t), Qx≤≤0,Q表示政府提供給企業的污水量,假設 Q足夠大;ξ企業實際能夠處理的污水量(萬t),是不確定變量,0≥ξ;p污水處理費用單價(元/t),0≥p;c處理污水的總成本費用單價(元/t),0＞＞cp;v政府對企業違約部分的懲罰率,0＞v;)(xμ污水處理企業收益(萬元).

2.2 模型構建

設企業實際能夠處理的污水量ξ是一個不確定變量,具有不確定分布Φ.如果企業污水簽約量是 x,則收益不確定函數μ(x)為

注:企業污水處理量ξ在年初簽訂合約時是一個不確定的量,但到了年終, ξ是具體的確定值.因此,算子min{x,ξ}雖然是不確定變量與確定變量的取小運算,實踐中仍然是有意義的.根據目標函數(1),考慮帶懲罰機制的污水處理問題,可建立如下期望收益模型.

定義 4 設污水處理企業的收益小于μ*的最大不確定指數要小于等于β,則基于不確定理論的污水處理期望收益模型為

式中:β為企業所能承受的最大不確定指數(0≤β≤1),μ*是污水處理企業的保守收益.

2.3 模型轉化與求解

模型(2)是不確定規劃,要用去不確定性的方法,將其轉化為等價的經典數學規劃求解.

定理 3 設政府對未完成污水量的總價值(x?ξ)p以懲罰率v進行懲罰,若ξ～L[a,b],則帶懲罰機制的污水處理期望收益為

證明 因ξ服從線性不確定分布 L [ a,b],分布函數為 Φ (t ) ,(t∈?+).μ( x,ξ)是關于ξ的單調遞增函數,將(1)式代入E[μ( x,ξ)],根據定理2及線性不確定分布 L [ a ,b]的性質[20-21]可得

積分可得

證畢.

對于約束條件

又ξ是一個不確定變量,根據文獻[20]可知μ( x, ξ)是 不 確 定 變 量 的 函 數,連 續 且 單 調,用D ( v ,β,μ*)表示可行解的集合,可得如下定理

定理4 模型(2)可行解集合具有下列性質:

(1)若 D ( v ,β,μ*)是空集,則污水處理企業就會放棄和政府進行簽約;

(2)若 D ( v ,β,μ*)非空,則

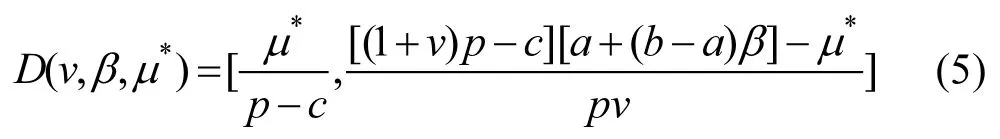
證明 將(1)式代入約束條件(4)式,可得

或

(1)由*式,有

此時企業不會選擇和政府簽約,即可行集D ( v ,β,μ*)是空集.

(2) 若 D ( v ,β,μ*)非空,對*式,可行解 x應滿足同理,對**式,有

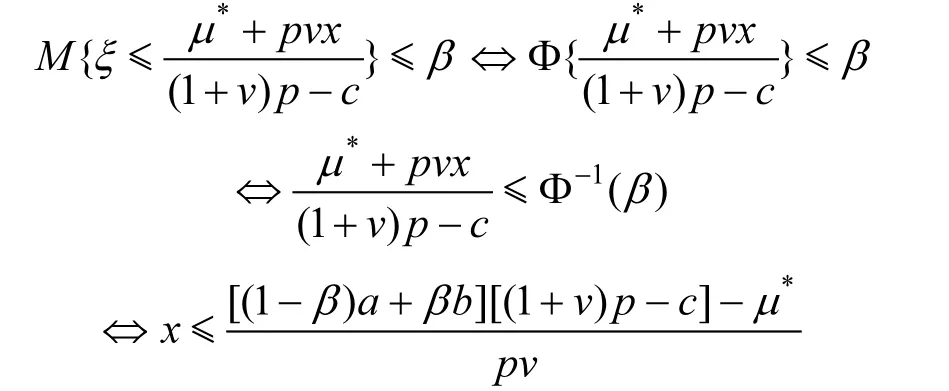
綜上所述,若 D ( v ,β,μ*)非空,則滿足

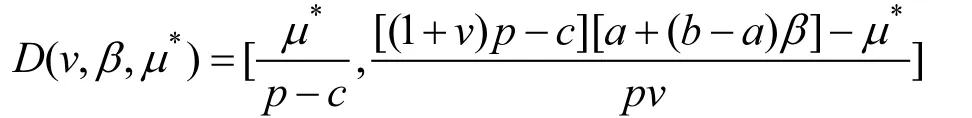
證畢.

因此,模型(2)可轉化為下列等價模型(6).

定義 5 不確定理論下帶懲罰機制的污水處理期望收益模型為

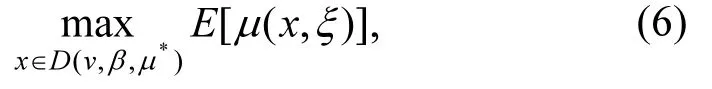
其中,E[μ(x,ξ)]滿足(3)式,x∈ D (v,β,μ*)滿足(5)式.

3 數值算例

政府以每噸 p = 3元將本城市部分污水委托給某企業處理,企業處理污水的成本為每噸 1=c 元,政府對未處理完污水量懲罰率為 1.0=v ,企業實際污水處理量]200,150[～Lξ, 即150=a萬t,200=b萬t.則基于不確定理論,帶懲罰機制的污水處理企業期望收益(3)式為

設企業保守收益為300萬元,則可行集(5)式為

若,05.0=β則模型(6)為

用Matlab軟件算出最優解 17.169=x 萬t,最大期望收益89.329=μ萬元.如圖1

圖1 期望收益和簽約量關系Fig.1 Expected return and contract volume

圖1中第1、2、4條豎線分別代表兩個區間:外圍區間 [1 50,200]為目標函數的分段區間,前面第1、2條豎線表示約束集 [1 50,507.5/3],第 3條豎線代表期望收益函數的全局最優解xq.分析圖1可知,當企業承受的不確定指數為 0.05時,企業受到可行集的約束.當x取最大約束值 xj=507 . 5/3(≈169.17)時,得到最大收益值為 329.89萬元.當 xj大于全局最優解xq= 1 93. 4 8時,函數圖中有極大值點(193.48, 343.48),此刻企業獲得穩定的最大收益值343.48萬元.

4 結果與分析

下面利用Matlab軟件的粒子群算法分別對模型中的參數:不確定指數β、懲罰率v、不確定度區間[a , b]取不同的值,求得相應的污水簽約量x和期望收益E[μ],然后再分別討論各個參數值的變化對結果的影響,及實際意義.

4.1 對不確定指數β的討論

結合上面算例,取

則計算如表1

表1 期望收益、簽約量和不確定指數的關系Table 1 Expected return, contract volume and uncertain index

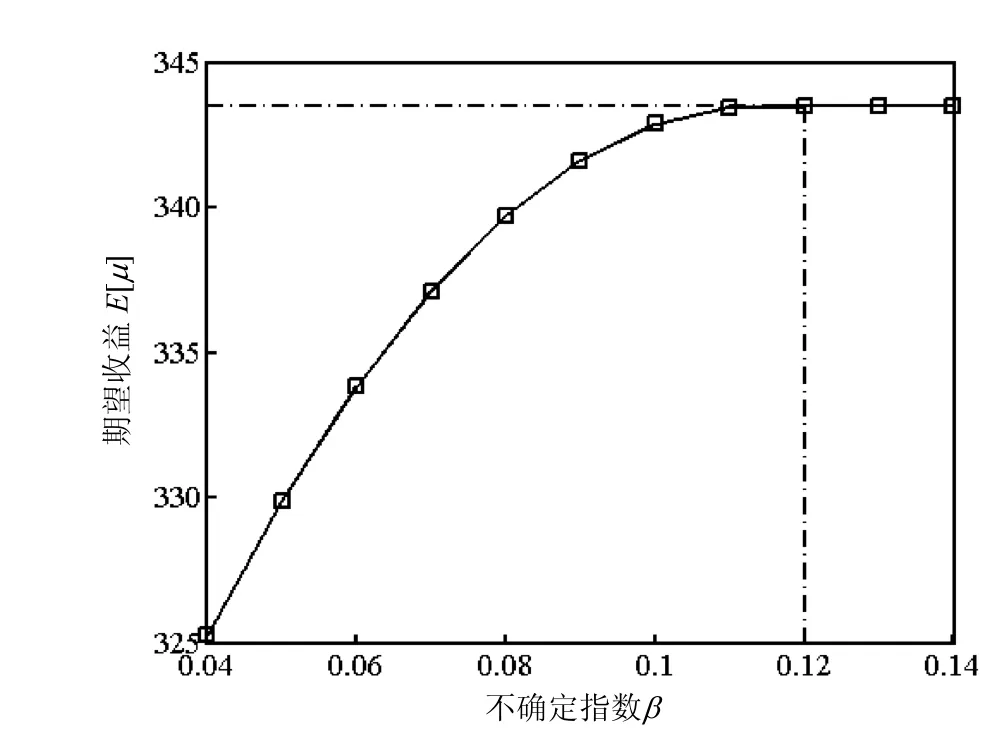
圖2 期望收益和不確定指數的關系Fig.2 Expected return and uncertain index

從圖2、圖3和表1可知,(1)懲罰率不變的條件下,隨著企業所能承受的不確定指數β的逐漸增加,簽約量逐漸增大,期望收益也快速增加.當β增加到 0.12時,][μE和x均達到最大值.(2)當β大于0.12以后,其對期望收益和簽約量將不在有影響.因為隨著β增大,可行集范圍漸漸擴大.可行集的右端點值已經超過了期望收益函數的全局最優解 48.193=q x ,之后全局最優解xq保持不變,且在企業污水處理能力范圍 ]200,150[之間,固然最大收益值不變(如圖1).

圖3 簽約量和不確定指數的關系Fig.3 Contract volume and uncertain index

4.2 對懲罰率v的討論

同樣地,結合上述算例取 p = 3,c = 1, μ*=300,β =0.05,[ a , b]=[150,200],可得

表2 期望收益、簽約量和懲罰率的關系Table 2 Expected return, contract volume and penalty rate

圖4 期望收益和懲罰率的關系Fig.4 Expected return and penalty rate

從圖4、圖5和表2可知,(1)給定不確定指數,隨著懲罰率的增大,簽約量逐漸減小,期望收益也減小.(2)當懲罰率達到0.7時,簽約量達到最大值154.88萬t,收益達到最大值308.79萬元.若懲罰率繼續增大,簽約量減小較為緩慢,懲罰率對簽約量的影響減小.此時,企業簽約量已接近無風險生產量a,企業違約的不確定指數比較低,懲罰對企業的影響較小;(3)當v較小時,x和E[μ]減小非常快,說明懲罰因子具有明顯遏制企業簽約量的作用.換句話說,懲罰因子較小時,企業簽約量較大,違約風險也較大,此時增加懲罰率,對企業道德風險具有明顯抑制作用.(4)若沒有懲罰因子,企業最大簽約量就會選擇為最大設計產能 200,此時企業違約風險很高.

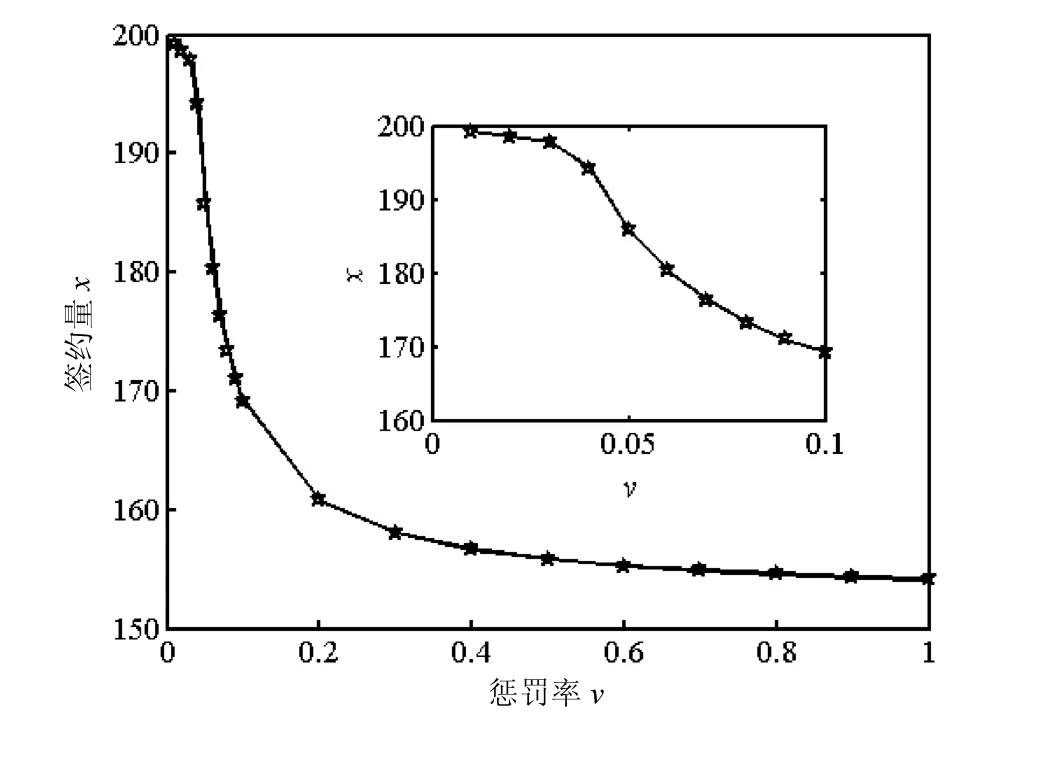
圖5 簽約量和懲罰率的關系Fig.5 Contract volume and penalty rate

4.3 對無風險處理量a的討論

類似上面取p=3,c=1, μ*=300, v = 0.1,β=0.05,可得模型為

表3 期望收益、簽約量和a值的關系Table 3 Expected return, contract volume and a value

當企業簽約量為a時,企業違約的不確定指數為0,a稱為無風險處理量.a與企業管理能力有關,如果管理水平高,影響正常生產的不確定因素就減少,企業無風險處理量就提高,收益也就增加.利用Matlab軟件計算如表3.

結合表3、圖6和圖7分析可知,在一定的不確定指數β和懲罰率v下,隨著無風險處理量a的取值逐漸增大,簽約量x逐漸增大,期望收益E[μ]也在逐漸增大.(1)從圖6中觀察到E[μ]一開始的增大趨勢相比x較大,這是因為在企業剛開始提高管理水平,降低不確定因素時,降低了企業的違約指數,也就大大的降低了企業違約的懲罰成本,此時,管理能力提高對企業的效益提高具有明顯的貢獻.(2)當a的值大于 110時,從圖6和圖7發現,x和E[μ]增加較為緩慢,這是因為隨著企業的無風險處理量a逐漸增加,企業的管理經營水平逐漸提升,經營管理水平提高對企業效益的顯著影響逐漸降低,也就是x和E[μ]的增加速度降低,這正好符合經濟學中的邊際效益遞減規律,因此出現了圖6和圖7的現象.綜上分析,建議企業應該加強內部控制與管理,降低影響污水處理的不確定因素,提高無風險處理量a,可有效的增加期望收益.

圖6 期望收益和a的關系Fig.6 Expected return and a

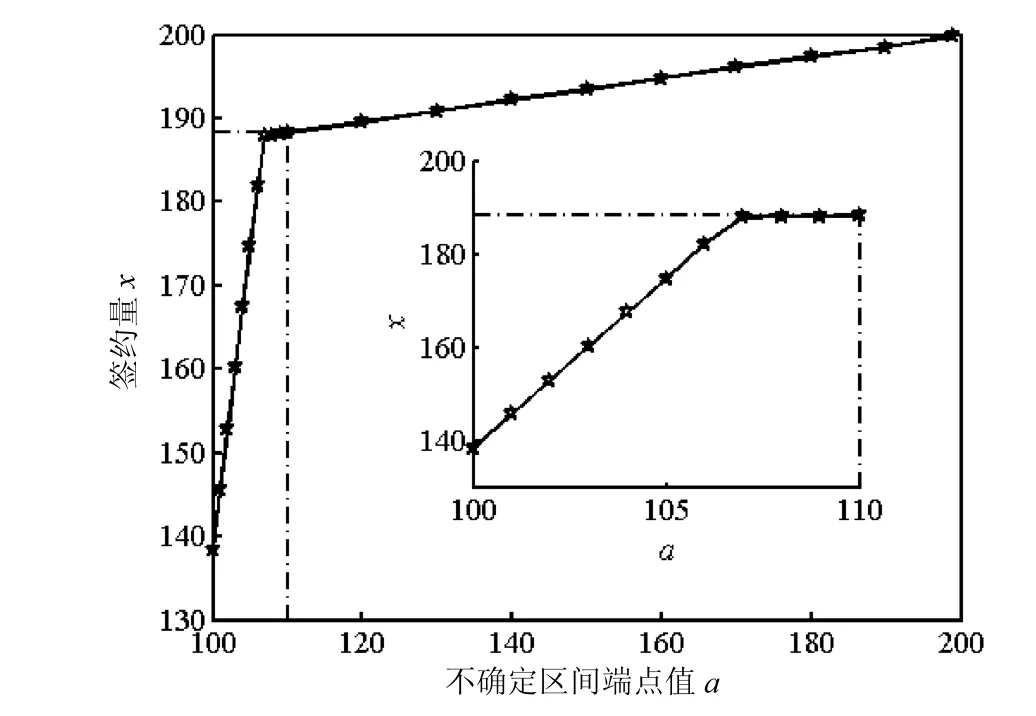
圖7 簽約量和a的關系Fig.7 Contract volume and a

5 結論

5.1 企業簽約量越大,收益越高,所承受的風險也越大.這符合企業生產與風險的經濟學現象.

5.2 懲罰率越高,企業簽約量越小,收益也隨之減少.說明懲罰因子起到了重要的作用:有效地降低了企業的投機行為和道德風險.

5.3 企業的無風險處理量越高,企業的簽約量越大,收益也越大.說明企業運行中要加強內部管理運營,努力提高無風險處理量.