基于非光滑方程組的智能電網實時定價

2018-07-26 01:52:58王宏杰

系統工程學報 2018年3期

王宏杰,高巖

(上海理工大學管理學院,上海200093)

1 引言

隨著科技的高速發展和生活水平的不斷提高,人們對電力的需求有了更高的要求.電力用戶希望電網是可靠的,安全的,經濟的,高效的.用戶希望可以實時了解供電能力,電能質量,電價狀況和停電信急,根據相關信急合理安排電器使用,避峰填谷;電力企業希望可以及時獲取用戶的詳細用電信急,合理安排生產,并為用戶提供更多的增值服務.現有的電網雖然已經開始實施分段電價,但是現有的電價定價機制是基于較長時間段上的價格變化,例如按白天和夜晚,冬季與夏季劃分時間段,每個時段制定不同的電價.這種實時定價研究已有較長的歷史并取得了一系列的研究成果,但是顯然這種定價機制不能完全滿足用戶和電力企業對電網的多樣化需求.所以近年來具有現代先進的傳感測量技術,通訊技術,信急技術,計算機技術和控制技術的智能電網引起了各國的高度關注和研究.美國,歐洲等發達國家目前都在發展智能電力系統,并且在智能電網領域取得了顯著的發展.相對于美國和歐洲,我國在智能電網的研究剛剛起步,研究還集中在智能電網定價機制和理念的研究上.所以智能電網短時段實時定價問題的研究對促進智能電網的發展至關重要[1?4].

目前在智能電網實時定價問題上主要從兩方面進行研究:一方面是從電力生產公司,電力銷售商等角度考慮的商業定價機制.例如,文獻[5,6]從供應商和需求側管理方面利用博弈的方法建立和研究實時定價問題,通過動態和靜態的博弈使價格趨于更合理.這類優化模型求解通常采用求均衡解的方法;另一方面是從公共產品角度考慮,追求社會效益的定價機制,根據社會效益最大化為目標建立優化模型,在總電量不超過發電能力前提下最大化用戶收益和最小化電力供應商成本.文獻[7–11]采用了社會效益模型,分別通過對偶法,乘子法和分布式算法來解決優化模型.利用乘子法,對偶法和分布式算法解決乘子問題,往往需要求解一系列無約束最小化問題,計算量大,數值不穩定,而且在算法中更多的注重資源的優化配置,電價被作為了資源配置的附屬問題.本文從社會效益定價機制方面出發,利用互補理論將社會效益模型轉化為帶有影子價格的非光滑方程組,通過求解非光滑方程組來確定短時段的實時電價.該方法可以避免數值不穩定,計算復雜等問題,并且電價作為重要變量被求出.

2 智能電網的社會效益模型

在電力市場中,不同用戶消費的電能也不同,即使消耗等價等量的電能也可能會擁有不同的滿意程度.在本文中,采用效用函數來反映消費者的電量消費能力和這種偏好,即效用函數表達了用戶對電能消費水平的滿意度.關于效用函數,假定消費者滿意度隨著使用電量的增加而增加直至達到飽和消費的最大滿意度,并且滿意度不會出現負滿意的情況(即效用函數小于零的情況).根據社會效益模型[9,10],定義電力用戶的效用函數和社會效益函數.其中效用函數為

是一個二次函數,x代表電力用戶的電力消費水平,它隨用戶與時間的不同而不同;α和ω是根據用戶在每個用電時段對用電量的不同要求和滿意情況選取的兩個非負參數.α是預先給定的,并且滿足0＜α≤1的常數;ω是隨著用戶和用電時段而改變的非負數,如圖1.

圖1 用戶效用函數(α=0.5)Fig.1 The utility function for powers subscribers(α=0.5)

假設共有N個電力用戶和1個電力供應商,每個用電周期分為K個時段.社會效益函數為

在電力系統中成本函數一般采用分段線性函數或二次函數表示[5?10],根據電力系統成本的常用計算方式,采用二次函數來表示成本,即

根據社會效益最大化,建立優化模型如下

因為實際生活中,在沒有突發事件的情況下用戶的實際消費水平往往小于該時段其最大需求量,所以在模型中只考慮實際生產能力不超過該時段最大生產能力的情況.根據模型(4)可以通過在K個時段里分別求社會效益最大來解決,所以模型(4)可以轉化為下面K個子優化問題,即

根據式(1)和式(3)的定義,可知式(5)是一個二次規劃問題.根據極值定理可以知道,對于二次規劃問題

其中f(x)為二次函數,g(x)=(g1(x),g2(x),...,gm(x))T,gi(x)為N元函數,x∈RN.

若x為問題(6)的一個最優解,則存在λ∈Rm使得x和λ滿足下列KKT條件

式(8)與式(5)等價,并且式(8)中的λ按經濟學上的解釋為電力資源的影子價格,所以可以通過式(8)來確定智能電網短時段的基礎電價λ.

3 算法構造

近年來,互補問題的研究得到了極大的重視和發展,并且在力學、交通及經濟等許多領域得到廣泛應用.形如

的問題被稱為互補問題,其中x∈Rn,F:Rn→Rn.顯然,式(8)是一個互補問題.取x和F(x)的第i個分量xi和Fi(x),為了書寫方便,記第xi=a,Fi(x)=b.根據非線性互補理論[12,13]有

所以式(8)等價于方程組

由于函數ψ(a,b)=a?max((a?b),0)在a=b處是非光滑的,因而式(10)是一個非光滑方程組,無法使用傳統的牛頓法求解.目前解決這類問題常用的方法是非光滑牛頓法和光滑化牛頓法.非光滑牛頓法是利用廣義牛頓類型即利用Jacobi矩陣求解;光滑化牛頓法是通過構造具有良好收斂性質的光滑函數來逼近非光滑函數求解.通過以往的研究和數值驗證,研究者們發現光滑化牛頓法具有良好的收斂性,并且在數值上比非光滑牛頓法更穩定和有效.因此本文采用光滑化牛頓法來求解問題(10).

首先介紹光滑化基本思想,假設一個非光滑方程組

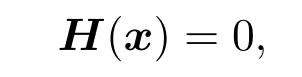
其中H(·):Rn→Rn是一個非光滑函數.再假設有一序列光滑函數Hμk(·):Rn→Rn,且滿足

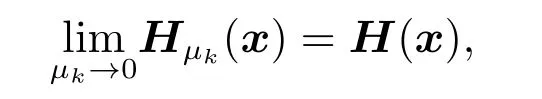
光滑化方法是希望通過求解光滑方程組Hμk(x)=0的解來逼近原方程組的解.

目前,構造光滑逼近函數常用方法有二次函數法,密度法,極大熵法等[12,13].為了保證解的逼近,光滑逼近函數應該滿足如下定義

定義1(光滑逼近函數)[12]給定函數H(·):Rn→ Rn,稱光滑函數Hμ(·):Rn→ Rn,μ ＞ 0為H(·)的一致光滑逼近函數,如果對任意x∈Rn,存在κ＞0,使得‖Hμ(x)?H(x)‖≤κμ,?μ＞0.

根據定義1和構造光滑函數的二次函數法,首先構造一個二次函數

下面證明函數ψμ(a,b)為ψ(a,b)的光滑逼近函數.

定理1函數ψμ(a,b)為函數ψ(a,b)的一個光滑逼近函數.

證明根據ψ(a,b)=a?max((a?b),0),可以得到

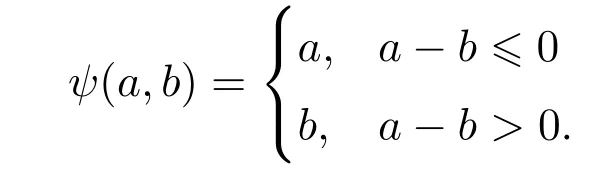
因為當?μ≤a?b＜0時,有

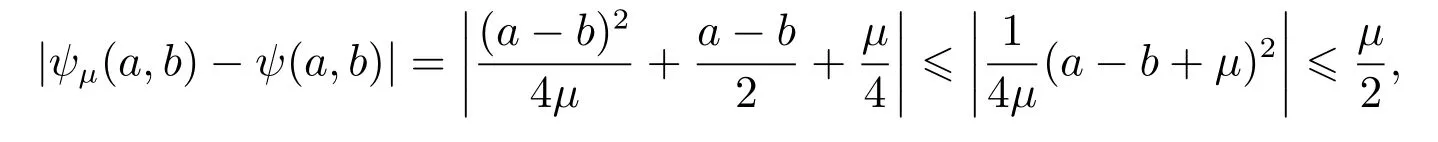
當μ≥a?b≥0時,有

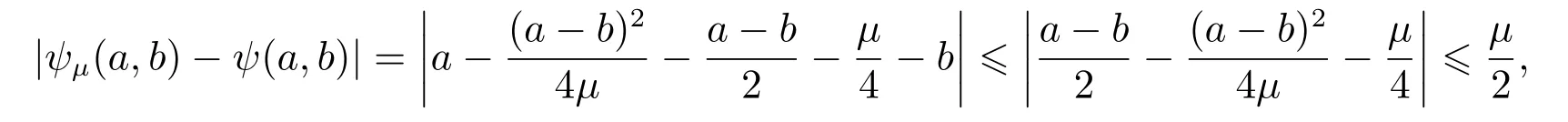
當μ＜a?b或?μ＞a?b時,有|ψμ(a,b)?ψ(a,b)|=0.

綜上所述,當取κ≥ 1/2時,對?μ＞0,有|ψμ(a,b)?ψ(a,b)|≤κμ成立.根據定義1,函數ψμ(a,b)為ψ(a,b)的一致光滑逼近函數. 證畢.

函數ψμ(a,b)在區間[?μ,μ]內的逼近情況如圖2所示.

圖2 非光滑函數ψ(a,b)與光滑逼近函數ψμ(a,b),在點a=b處的逼近情況,?=a?bFig.2 The approximation of nonsmooth function and smooth function at point a=b,? =a?b

根據定理1,可知光滑函數ψμ(a,b)具有良好的收斂性并且隨著參數μ減小逐漸逼近ψ(a,b),滿足光滑化方法對光滑函數的要求.因此根據ψμ(a,b)和式(10)中F(x,λ)的構造方法,定義光滑逼近函數Fμ可以得到光滑方程組

而式(13)即為要求解的問題.為了書寫方便將變量x和λ記為變量X=(xT,λ)T.

因為利用擬牛頓法解方程組(13),可以避免Hesse矩陣退化的情況,而且還可以同時求出變量和電價λ,所以本文選用擬牛頓法求解方程組(13).根據擬牛頓法的PEF修正迭代公式[12,13]有

因為用戶使用電量不能是負值,為了確保λ是在變量x≥0時的影子價格,解方程組(13)時,只取x≥0時的解.

算法步驟如下:

步驟1取初始點X0≥0,其中參數λ0∈(0,100),取參數Lk,選取足夠小正數ε.令k=0,H0=In,μ=0.05;

步驟2判斷‖Fμ(Xk)‖＜ε是否成立,若成立則停止迭代,Xk即為所求;否則轉步驟3;

步驟3令dk=?HkFμ(Xk),解優化問題Min‖Fμ(Xk+δdk)‖得到最優解δk.Xk+1←Xk+δkdk,轉步驟4;

步驟4令Pk=Xk+1?Xk,Qk=Fμ(Xk+1)?Fμ(Xk),▽HkHk+▽Hk,k←k+1,轉步驟2.

4 仿真模擬

取ak=0.01,bk=0,ck=0,α=0.5,ω∈[1,4],μ=0.05,N=6.以24 h為一個用電周期,那么在用電周期中,總電量的使用情況是由低到高再到低,在仿真中Lk的取值符合這樣的形態.通過仿真模擬,得到了每個時段的實時電價λ以及電量的最優分配.同時,將新方法與固定電價方法進行了比較.其中固定電價方法的定價公式[10]為λk=ωmax?Lkα/N.結果如表1～表4及圖3～圖6.

表1 基于非光滑方程組方法和固定電價方法的電價(1)Table 1 The electricity price based on non-smooth equations method and traditional fixed price method(1)

表2 基于非光滑方程組方法和固定電價方法的電價(2)Table 2 The electricity price based on non-smooth equations method and traditional fixed price method(2)

表3 基于非光滑方程組方法和固定電價方法的社會效益(1)Table 3 The social benefit based on non-smooth equations method and traditional fixed price method(1)

表4 基于非光滑方程組方法和固定電價方法的社會效益(2)Table 4 The social benefit based on non-smooth equations method and traditional fixed price method(2)

圖3 基于非光滑方程組方法的智能電網生產能力Fig.3 The power Capacity of smart grid based on non-smooth equations method

圖4 基于非光滑方程組方法的每時段總分配電量Fig.4 The total power distribution per time interval based on non-smooth equations method

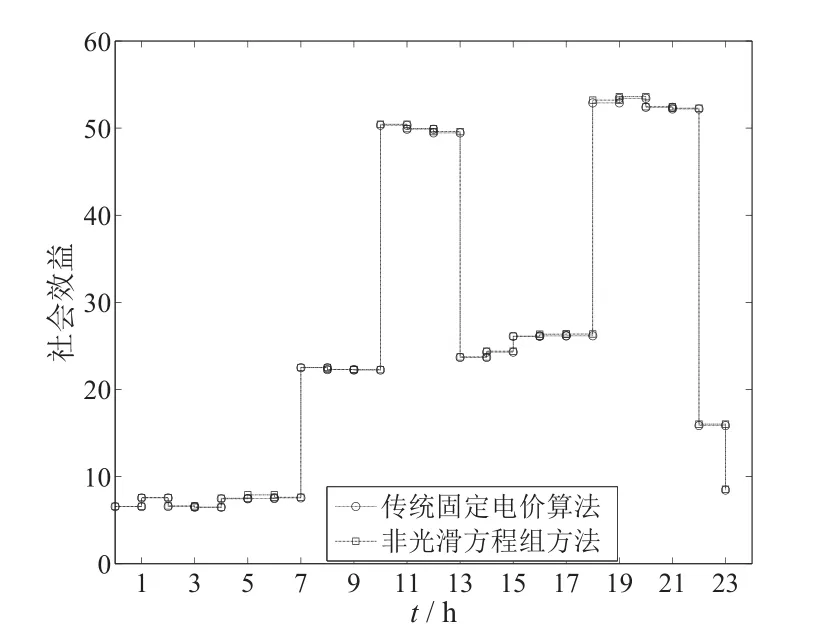
圖5 基于非光滑方程組方法與傳統固定電價方法的社會效益Fig.5 The social benefit based on non-smooth equations method method and traditional fixed price method

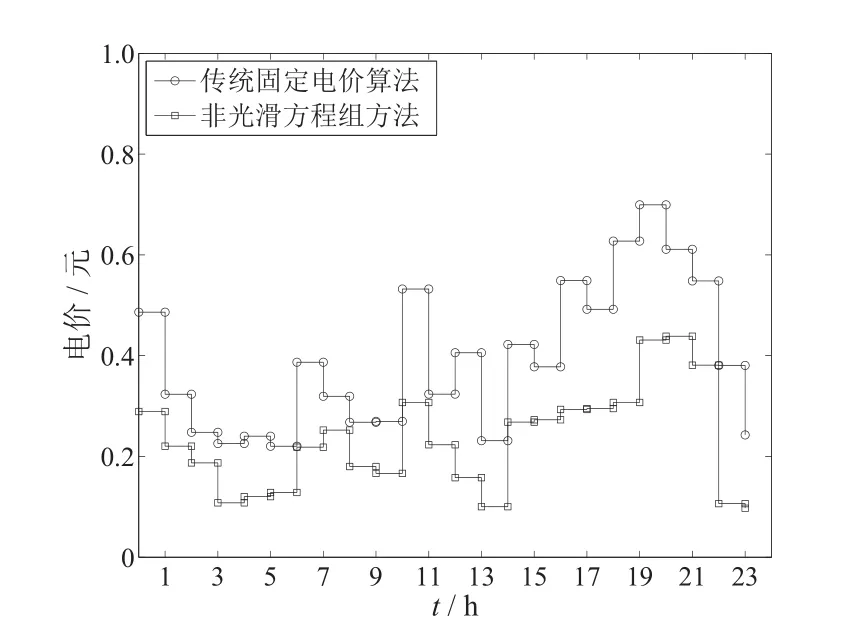
圖6 基于非光滑方程組方法與傳統固定電價方法的短時段電價Fig.6 The short time interval price based on nonsmooth method and traditional fixed price method

從圖3和圖4可以看出,當實際生產的電力資源被完全分配時,資源得到最優配置.從圖5和圖6可以看出,與固定電價方法相比，新方法得到的社會效益要略高于固定電價方法,但是新方法計算的電價更低.這是因為每個用戶對電量消費水平的滿意程度不同.固定電價方法傾向于平均分配電力資源,沒有考慮用戶的電量消費水平滿意度;而新方法考慮了用戶的電量消費水平滿意度,優先分配滿意度高的用戶,所以在社會效益相近的情況下,利用新方法得到的電價更低.該結果與文獻[9,10]中的結果相符,所以利用新方法解決智能電網實時定價問題是有效可行的.

5 結束語