基于VMD的諧波檢測方法
陳強偉,蔡文皓,孫磊,牛春光
(西安科技大學 電氣與控制工程學院,西安 710054)
0 引 言
近年來由于電力電子器件的發展,使得大量的非線性負載運用到電網中,由此引起的電能質量問題得到了社會的廣泛關注,而諧波對于電網的污染首當其沖[1-3]。隨著新能源在電力的快速發展,使得各種分布式電源應運而生,比如光伏發電、太陽能發電和風力發電等等,這些小型的發電設備并網運行時,同樣也給電力系統帶來了一系列的諧波污染問題[4]。
諧波污染問題會給電網帶來各種不良的結果,其中最為重要的表現如下:諧波諧振會使得電力系統過電壓,造成電力網絡中的電氣元件老化與損毀;增加發電機系統額外的諧波損耗和發熱,大大縮短了發電機的運行時間;在繼電保護中會使得敏感的電氣保護元件誤動和拒動;對通信設備產生電磁干擾,將很大程度上減弱了通信質量[5]。
一直以來,許多學者專家關于諧波檢測問題進行了大量的探索與研究,提出了一系列諧波檢測的有效方法。具體方法有:瞬時無功功率理論(p-q和ip-iq)算法[6-7]、Fryze功率理論算法[8]、傅里葉變換算法[9-10]、小波變換算法[11-12]、自適應濾波算法[13-14]、神經網絡算法[15]、經驗模態分解[16-18]等算法。瞬時無功功率理論算法雖然能準確的檢測出諧波分量,但是實現方法數學公式較多,實現困難,并且要求電網電壓無畸變這一理想條件。Fryze功率理論算法同樣是要求電網電壓無畸變這一理想條件。而傅里葉算法只在信號穩定時檢測結果較為精確,但在非穩定信號傅里葉算法并不能檢測出來。雖然小波變換算法恰好克服了傅里葉變換的缺點,但是小波變換要對小波基函數進行選擇,不同的小波基函數所檢測出來的諧波分量也有一定的影響。自適應濾波算法和神經網絡算法需要大量的檢測樣本這一前提條件,并且自適應濾波算法的迭代步長不太好控制。EMD雖然實現簡單,但是得到的模態函數容易產生虛假分量和模態混疊。在上述方法進行諧波檢測之中,有許多算法需要用到低通濾波器來提取基波分量,然后用待檢測信號減去基波信號得到所要檢測的諧波分量。顯然,低通濾波器對檢測結果準確性有著一定的關系。
VMD是一種新提出的對信號進行時頻變換的方法[19],它的分解結果與EMD有著相似之處,但是它與EMD算法的原理截然不同。VMD算法通過迭代搜索變分模型最優解以此來提取每一個分量的中心頻率及帶寬,從而得到本征模態分量。同時VMD算法可以抑制噪聲和沖擊信號所引起的模態混疊這一不利因素。VMD算法已成功的運用到風電機組故障診斷[20]、機械故障診斷[21]、變壓器的放電去噪[22]中。本文首次將VMD算法運用于電網的諧波檢測當中,通過VMD算法將含有諧波分量信號分解為本征模態分量,然后對每一個本征模態分量進行Hilbert變換,找出基波的幅值和頻率參數,最后將電力待測信號減去所提取的基波信號,即可檢測出電力網絡的諧波。該方法對電網的電壓沒有任何要求,在實現過程中也無需用到低通濾波器,所檢測出來的諧波具有很高的精度。
1 變分模態分解算法
VMD算法是由加利福尼亞大學的Konstantin Dragomiretskiy等人2014年提出的一種新的可變尺度信號分解方法。VMD算法是利用迭代搜索變分模型最優解的方式來提取每個IMF分量,它可以把一個復雜的信號分解為K個IMF分量信號,因為K值是我們自己選定的,如果K值取得合適,那么就可以避免待檢測信號由于模態混疊現象而給分解帶來的不利影響。
1.1 本征模態分量
對于任意個IMF分量都可以看成是一個調幅-調頻信號,其可表示為:
uk(t)=Ak(t)cos(φk(t))
(1)
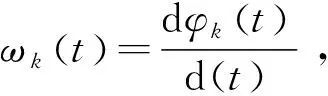
1.2 變分模型
VMD算法的核心是將一個待檢測信號x分解成許多個本征模態分量uk(t),這些uk(t)可以通過如下方式計算得到:
(1)對uk(t)進行Hilbert變換,就可以獲得uk(t)的解析信號,從而計算出uk(t)的單邊頻譜。
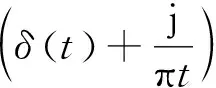
(2)
式中δ(t)為單位脈沖函數;j為虛數單位;*表示卷積。
(2)對模態分量uk(t)的解析信號估計它的中心頻率e-jωkt,然后將每一個uk(t)的頻譜調制到與它相對應的基頻帶。
(3)
(3)最后計算式(3)解調信號的梯度的L2范數的平方。
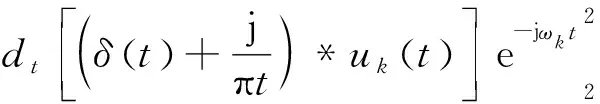
(4)
式中dt為函數對時間t的偏導數。
通過步驟 (1)~步驟(3)得到變分約束模型為:
(5)
式中uk={u1,u2,…uk}為模態的集合;ωk=(ω1,ω2,…ωk)為相對應中心頻率的集合。
上述變分約束模型實際上是一個約束的最優化問題,為了求解上述優化問題,利用二次懲罰項和拉格朗日乘子法引入增廣Lagrange函數η。
1.3 變分模型的求解
對于式(5)引入增廣Lagrange函數η后可得:
η({uk},{ωk},λ)=
(6)
式中α表示罰參數;λ為Lagrange乘子。
利用交替方向乘子算法求解式(6)變分模型增廣Lagrange函數η的最優解。
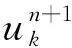
(7)
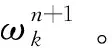
(8)
將公式(8)轉換為非負頻率區間積分的形式:
(9)
則變分問題的解為:
(10)
同樣求得中心頻率ω(k)的更新為:
(11)
其中迭代停止準則 :
(12)
從對求解步驟來看,VMD算法是將每一個本征模態分量直接在頻域上在更新結束后滿足停止準則的前提做一系列的更新。
2 基于VMD的諧波檢測
根據前面第1節所述的變分模態分解算法,將電網的待測電流作為復雜信號x。接著按以下步驟:
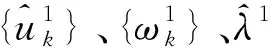
(2)對于n=n+1執行整個迭代;
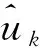

(13)
式中γ代表噪聲容限參數。為了分解結果不受噪聲影響,可讓γ=0。
(5)循環步驟(2)~步驟(4)直到當滿足式(12)的迭代停止準則。
3 算例仿真和實測數據分析
3.1 算例1
假設在一個含有諧波的電流信號為:
x(t)=100sin(100πt)+30sin(300πt)+
20sin(500πt)+10sin(700πt)
(14)
由式(14)可知該電流信號一共含有四種成份,公式的第一項為電流的基波成份,并且幅值為100,頻率為50 Hz。公式的后三項分別為3次、5次和7次諧波,其幅值分別為30、20、10。電流信號的采樣頻率為5 000 Hz,采樣點數為5 000(這里取前2 000個點)。圖1是該電流信號的原始波形圖。對x(t)分別進行VMD和EMD分解,獲得的IMF如圖2和圖3所示。
由圖2可知,VMD分解能夠很清晰的分解出含有諧波的電流信號的四種分量,使得分解結果很合理。而圖3 EMD分解出來的四種分量,雖然50 Hz和150 Hz的分量能夠清晰的分解出來,但是對于250 Hz和350 Hz的分量的分解不盡理想,分解出來的也不是正弦波,誤差很大。EMD分解的不合理是因為所假設的諧波的電流信號存在嚴重的模態混疊現象,而VMD分解能抑制模態混疊現象,所以二者的分解結果存在著差異。現在單獨對這兩種分解結果下的基波做Hilbert變換。圖4和圖5分別代表了VMD和EMD分解下基波的Hilbert變換。
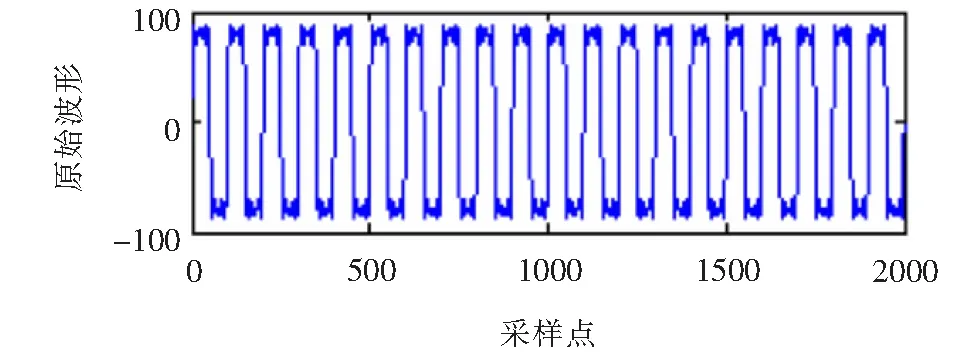
圖1 諧波信號
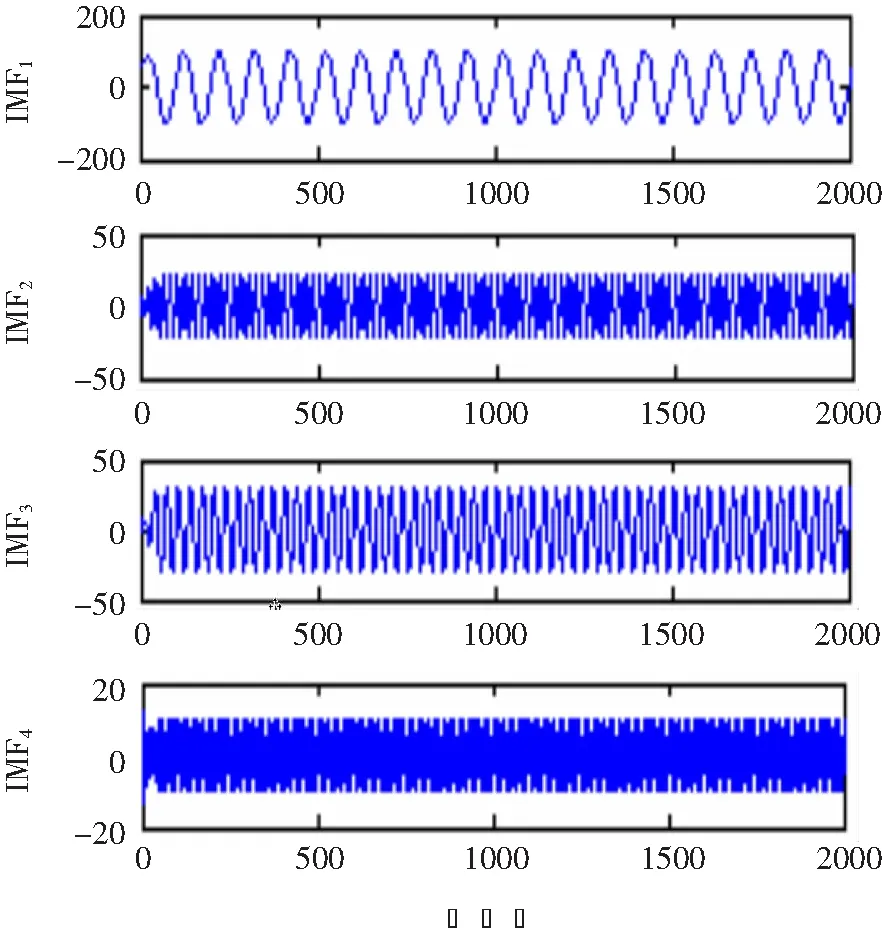
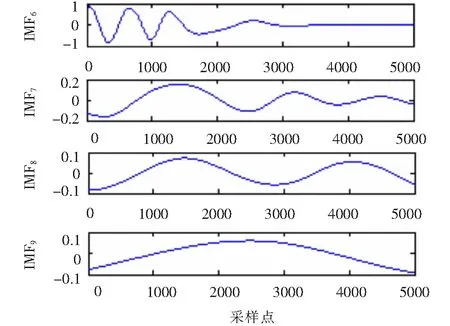
圖2 VMD分解結果
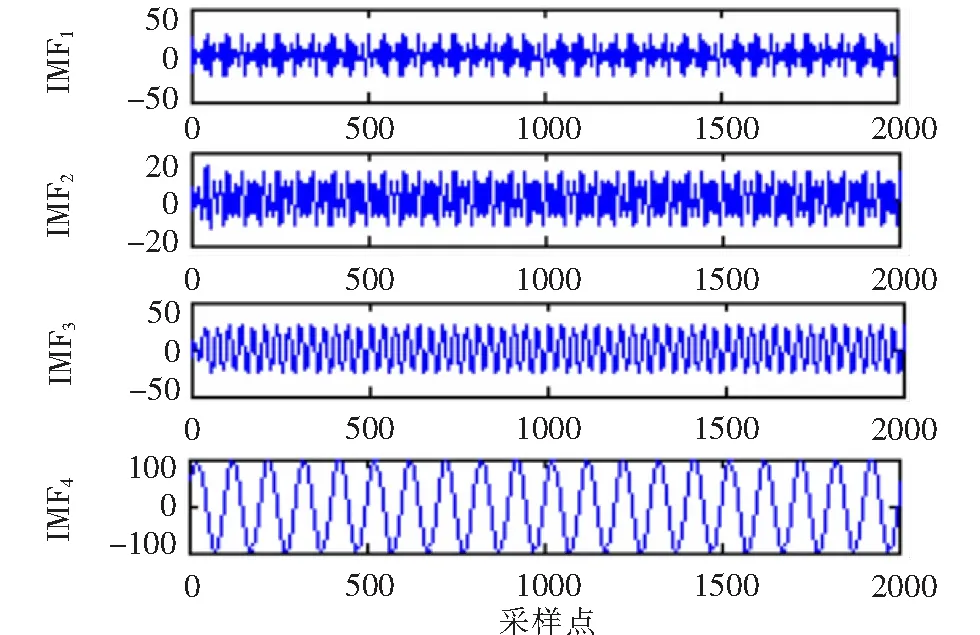
圖3 EMD分解結果
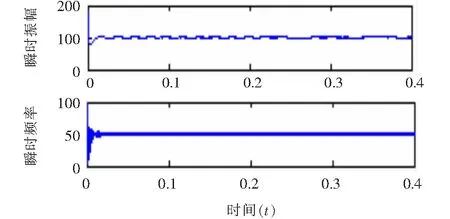
圖4 VMD分解基波的Hilbert變換
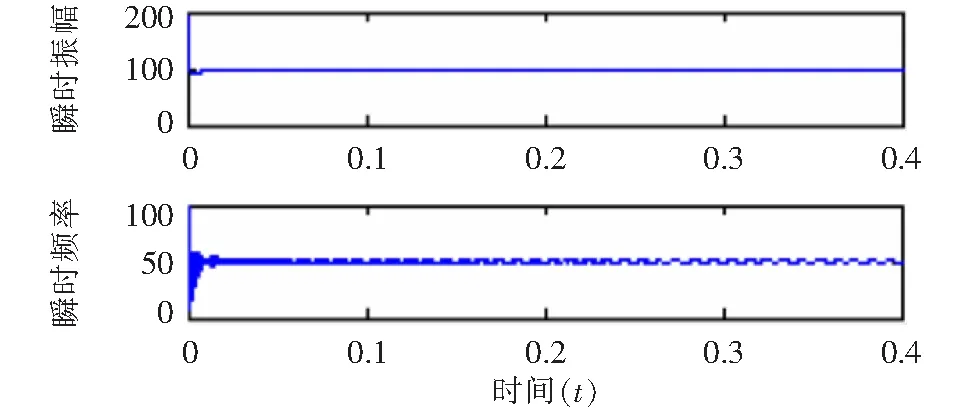
圖5 EMD分解基波的Hilbert變換
利用平均值求出以上兩種分解方法基波頻率和幅值的估計值,在VMD分解下,基波頻率的估計值為49.916 3 Hz,幅值的估計值為99.780 5。在EMD分解下,基波頻率的估計值為49.923 1 Hz,幅值的估計值為98.764 9。相比之下,兩種分解方法對于基波都能準確的分解出來,但是從整體來看VMD分解比EMD分解更能表達原始波形的信息。
3.2 算例2
假設信號x(t)是一個含有諧波的非穩定信號且為:

(15)
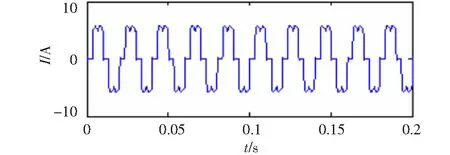
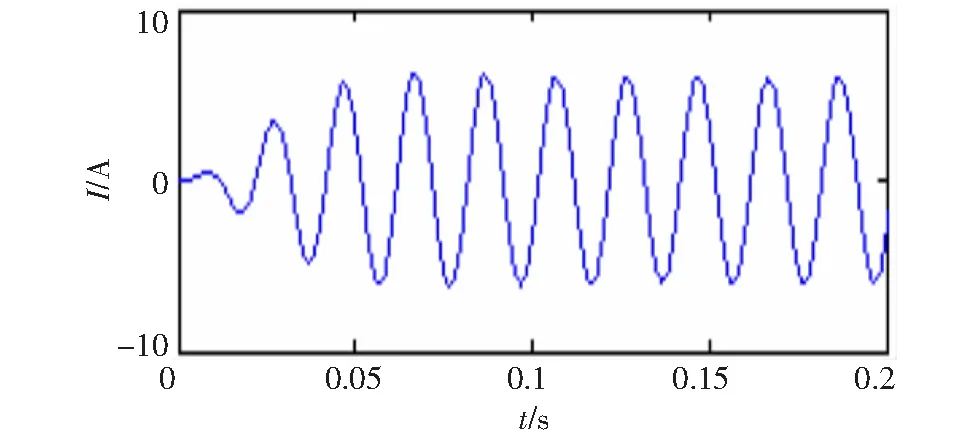
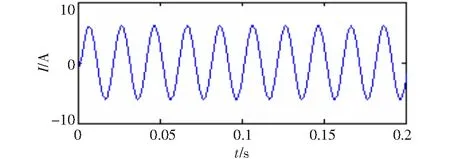
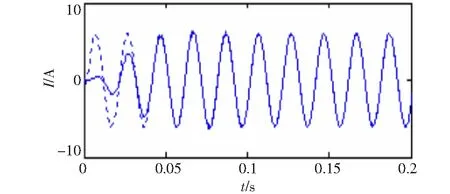
由式(15)可知非穩定信號同樣有四中分量,基波信號一直都有,在0.1 s 圖6 VMD分解結果 圖7 EMD分解結果 由圖6可知,IMF1代表了基波分量,IMF2代表250 Hz的諧波分量,IMF3代表150 Hz的諧波分量,IMF4代表350 Hz的諧波分量。VMD分解的結果清晰準確,基本無誤差。現在單獨分析的基波信號,對IMF1做Hilbert變換結果如圖8所示。 圖8 VMD分解基波的Hilbert變換 利用平均值得出VMD分解方法基波頻率和幅值的估計值分別49.929 8 Hz和99.740 2,所求出的頻率誤差為0.140 4%,幅值誤差為0.259 8%。所以對于VMD分解結果比較準確。而對于圖7 EMD分解結果,所分解的第二項為基波,但是在前500點出現了模態混疊現象,使得分解的基波并不完整,失去了原來諧波信號的物理意義。并且EMD分解的結果出現了虛假分量。對于分解結果,顯然VMD分解比EMD分解更為精確,更能體現原來諧波信號的信息。 為了更好的說明所提出的VMD分解方法的有效性,諧波源采用比較常見的三相橋式晶閘管的整流電路的實際信號,并且將VMD的檢測結果與瞬時無功功率p-q法的檢測結果做比較。 圖9 a相電流 三相橋式晶閘管的整流電路觸發角α=00,電源為三相對稱的并且幅值為220 V,頻率為50 Hz。采樣頻率為50 000 Hz,采樣點數為20 000個。圖9是所給電路中a相負載側電流ia的波形圖。 利用瞬時無功功率p-q法所提取的基波電流ipq如圖10所示。 對ia做VMD分解變換,得到的基波電流iV如圖11所示。 圖10 基波分量ipq 圖11 基波分量iV 現在將兩種方法所求得的基波分量通過同一坐標下進行比較如圖12所示。圖中實線為瞬時無功功率p-q法所求得的基波分量,虛線為VMD所求得的基波分量。從圖中可看出,當所求得的基波分量穩定后兩種發放所得到的基波分量基本一致,并且VMD算法具有更快的收斂時間。 圖12 VMD算法與p-q法檢測基波分量對比圖 為進一步檢驗VMD方法的檢測效果,分別對這兩種方法所求得的基波ipq和iV做Hilbert變換,再利用平均值計算出兩種方法所檢測出的基波的幅值和頻率的估計值(為了消除邊界效應的影響取中間的數據進行計算)。p-q法所求得結果的估計值為:頻率49.993 9 Hz,幅值為6.007 7;VMD法所求得結果的估計值為:頻率50.000 3 Hz,幅值5.996 0。通過數據的比較,相對頻率來說VMD法比p-q法更為準確。對于幅值,將ipq作為參考量,幅值的平均誤差為0.194 8 %。所以對于VMD方法所求得的基波分量無論是從圖直觀看還是實際數據都表明了是非常準確的。 首次提出基于VMD的諧波檢測,通過算例仿真和瞬時無功功率p-q法對比實測數據證明,該方法能準確的檢驗出電網中的諧波分量。與EMD算法相比,該算法能有效的抑制模態混疊現象,分解出的結果也不含虛假分量,對非穩定信號也能進行準確的分解。VMD算法在進行諧波檢測時,無需用到低通濾波器,可很大程度上減少檢驗誤差。本文提出的算法不僅能用在單線電路的諧波檢測,也可以用在三相三線制和三相四線制電路中,而且該算法不需要電網電壓有無畸變這一條件。并且該算法不僅能檢驗出諧波,并且能檢驗出信號中的特定次諧波和間諧波,對分解出的IMF分量做Hilbert變換即可實現,具有很高的推廣價值。


3.3 算例3
4 結束語

