長耳鸮翼型氣動及聲學特性研究

張 康，楊愛玲，董云山，陳二云，戴 韌

（上海理工大學 能源與動力工程學院, 上海 200093）

流動效率、噪聲是風機、水泵、風力機等葉輪機械的重要性能指標，高流動效率、低噪聲的葉輪機械一直是研究人員和制造商努力追求的目標。然而，隨著設計水平與控制技術的提高，許多目前比較常用的翼型流動及噪聲性能優化方法已經遇到了瓶頸，在這種情形下，仿生技術成為一個十分重要的研究方向。

長耳鸮具有靜音飛行的特點，這可能與其翼型有密切的關系。目前已有研究確定鸮翼噪聲（散射噪聲）與飛行速度的5次冪有關［1］，而鸮還能有效降低2 kHz以上的高頻噪聲。Graham［2］認為鸮類具有的天鵝絨般覆羽、鋸齒狀前緣和干涉狀后緣是降噪的主要原因。鸮類飛行時，空氣掠過其翅膀時的流動狀態與結構是決定鸮升力大小的關鍵因素，因此，可以推斷鸮類翅膀截面形狀與鸮類氣動以及其空氣動力噪聲有著內在聯系。Kondo等［3］對鸮翅膀40%截面處的鸮翼繞流流場進行數值模擬的結果表明，在低雷諾數下鸮翼升阻比較NACA0002和NACA0012等標準翼型均有提高，這說明該截面處的鸮翼有著良好的氣動性能。王星等［4］以某長耳鸮翼型為仿生研究原型，通過正交試驗研究發現，翼型前緣厚度對仿生翼型升阻比影響最大，隨著翼型前緣厚度減少，翼型升阻比增加，翼型下表面中部曲率和翼型尾部厚度均存在使仿生翼型升阻比最大的最優值。李典等［5］通過對于海鷗、秋沙鴨、水鴨以及鸮等鳥類翅膀40%截面處翼型繞流場的數值研究發現，頻譜圖中鸮翼型聲壓級明顯低于其他三種翼型，這說明鸮翼的特殊結構具有良好的氣動聲學特性。上述研究表明，長耳鸮翅膀翼型與流動特性有密切聯系，然而對于長耳鸮整體翅翼各截面的流動特性及其對噪聲的影響尚未見報道，故本文將對此展開較為深入的研究。

本文采用數值方法對長耳鸮翅膀展向20%、40%和60%截面處翼型流場及流動誘導聲場進行研究，分析其流動及噪聲性能。將三種翼型進行性能對比，利用計算流體力學模擬繞仿生翼型的非穩態流場，分析可能產生擾動的流場結構。

1 長耳鸮翅翼幾何參數

由于某長耳鸮翅膀展向20%以下、80%以上截面翼型與展向20%和60%處翼型相似，因而本文對其翅膀展向20%、40%及60%三個典型截面處的翼型性能進行研究，相應的翼型幾何參數來源于文獻［6］。根據文獻［6］，長耳鸮翅膀最大彎度Zc，max和最大厚度Zt，max沿翅膀展向分布有

式中：c為翅翼弦長；ξ為展向相對位置，ξ =y/b，y為展向坐標，b為翅膀展長。

文獻［6］同時擬合了各相對展向位置的翅翼的中弧線和厚度分布，得到了光滑的翼型及具體翼型參數。圖1為長耳鸮翅膀20%、40%和60%相對展向位置的翼型形狀，可以看出：翅根側20%截面處翼型前緣半徑、最大彎度和最大厚度是三者中最大的；而翅尖側60%截面處翼型前緣半徑及彎度均最小，厚度沿弦長的分布也較為平緩；40%截面處翼型形狀介于前兩者之間。三個截面處翼型均在翅膀飛行做功過程中發揮了作用，因而通過研究可以了解到各個剖面翼型對長耳鸮飛行所作的貢獻。

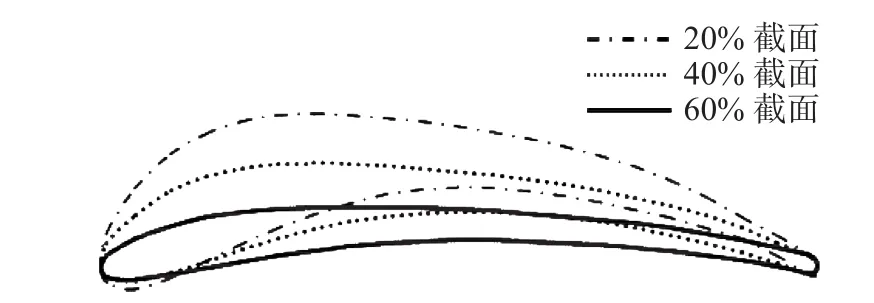
圖1 某長耳鸮翅膀展向三個截面處的翼型形狀Fig. 1 Airfoil shape of three bionic airfoils based on the long-eared owl wing

2 數值計算方法

2.1 計算網格及邊界條件

圖2為二維翼型繞流計算域和網格示意圖。為了合理地給出邊界條件，計算域進口和出口分別位于翼型前緣上游9倍弦長和下游20倍弦長處。為了提高近翼型區域計算網格的正交度，合理布置計算域網格疏密分布，本文采用多區域法進行網格劃分，其中近壁區為O型網格，翼型表面法向第一層網格y+＜1，且翼型表面附近的計算域采取加密處理，如圖2(b)所示。

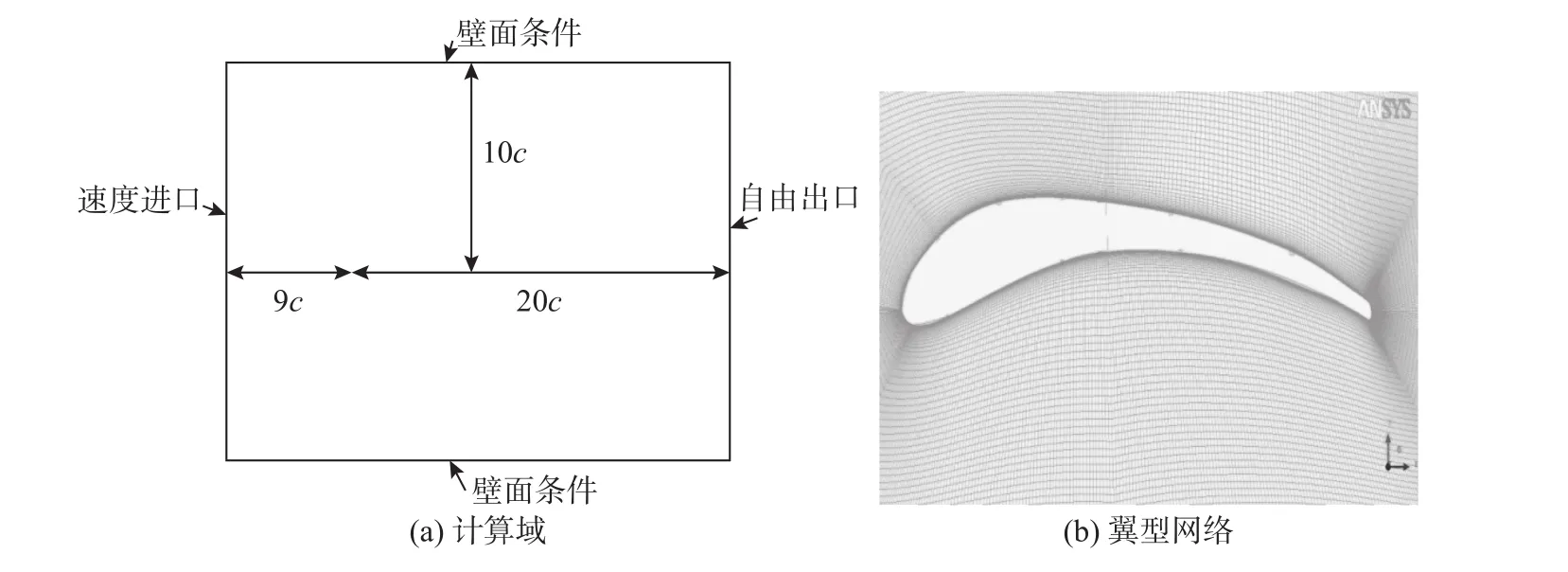
圖2 二維翼型繞流計算域及網格示意圖Fig. 2 Computational region of 2-D airfoil flow and its meshing

本文采用的計算域邊界條件有速度進口、自由出流出口邊界和無滑移壁面邊界條件，其中進口速度均為30 m·s?1，進口雷諾數Re約為4 ×105。為了模擬鸮翼在不同來流攻角（來流方向與翅翼弦長的夾角）下的性能，本文通過改變進口速度方向，在? 5°～20°攻角范圍內對翼型非定常湍流場進行計算。

為了驗證數值計算結果與網格的無關性，本文首先以40%截面處的翅翼為例進行了網格無關性驗證。圖3給出了翼型0°攻角下分別取15萬、30萬、45萬、60萬和75萬網格時的升阻比CL/CD（CL為升力；CD為阻力）曲線，可以看出：網格數從30萬增加到75萬時升阻比增加量約為網格數從15萬增加到30萬時增加量的1%，因而認為網格高于30萬時，升阻比基本不再隨網格數增加而發生改變，表明數值解已不依賴于計算網格。本文綜合考慮，將計算網格數保持在30萬左右。

2.2 數值方法

鳥類飛行時特征速度一般為20 m·s?1左右，故流體繞流翅膀的流動屬于不可壓縮流動，因此本文采用不可壓縮N?S方程作為流動控制方程，應用Spalart?Allmaras單方程模型進行湍流模擬。控制方程的離散格式為二階迎風格式，采用SIMPLEC算法求解離散控制方程組。為了捕捉翅翼表面的湍流特征，本文在繞流場定常數值解基礎上啟動基于大渦模擬技術的非定常流場計算，亞格子尺度模型為Smagorinsky?Lilly模型。在數值計算時，時間步長取為4 × 10?5s。為驗證其合理性，首先對20%截面處翼型非定常流場進行了試算，并將監測到的翼型升力和阻力系數經快速傅里葉變換后發現，翼型升阻力脈動主頻約為160 Hz左右。該脈動周期約為0.006 25 s，遠大于計算所取時間步長，因而判斷所取時間步長可以滿足模擬計算要求。

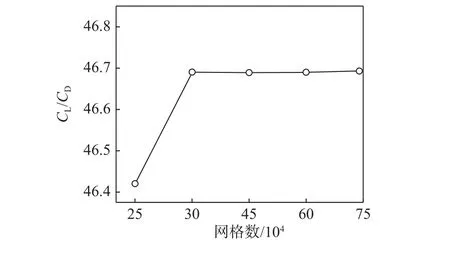
圖3 40%截面處翅翼升阻比隨計算網格數的變化(α =0°, Re = 4 × 105)Fig. 3 Influence of mesh number on the lift-drag ratio of the airfoil at the cross section of 40% (α = 0°,Re = 4 × 105)

本文采用聲學軟件Actran計算翼型流場對于遠場的聲輻射。該軟件是基于Lighthill聲類比理論［7］的有限元聲學軟件。對于靜止固壁繞流誘導的氣動噪聲問題，Actran軟件通常采用Lighthill體聲源方法計算，即將繞翼型的一定區域定義為體聲源區，聲源區外為聲傳播區。在聲源區，流場速度是Actran計算聲源的基礎。本文通過非定常流場計算獲得一定時間段內聲源區所有網格點的速度信息。在聲傳播區，由于本文研究的翼型繞流馬赫數Ma相對較低（Ma ＜0.1），故可忽略聲傳播區背景流動對聲輻射的影響，所求解的聲學方程可為

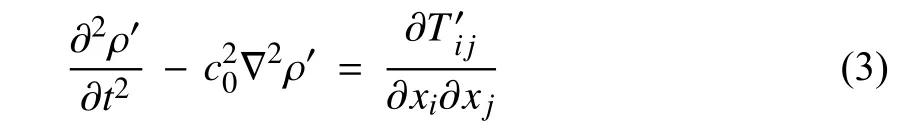
式中：ρ′為流體密度波動量，ρ′ = ρ?ρ′0，ρ、ρ′0分別為擾動、未擾動時的流體密度；t為時間；c0為等熵條件下的聲速；為Hamilton算子；i、j為笛卡爾坐標系兩個坐標分量；為Lighthill應力張量。

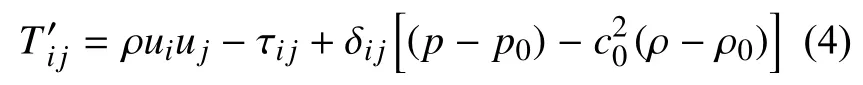
式中：ui、uj分別為液體速度矢量在xi、xj方向上的分量；為黏性應力張量；p、p0分別為擾動、未擾動時流場壓力。

為了模擬聲在無限區域傳播，將最外圍邊界區域定義為無限元區域，模擬遠場輻射，假設聲音在此區域內可自由傳播，沒有反射。

3 計算結果分析

3.1 翼型的氣動特性

圖4為20%、40%和60%截面處翼型升阻力系數及升阻比。從圖中可看出，40%截面處翼型升力系數在大多數攻角下都比其他兩種翼型的要高，60%截面處翼型升力系數最小。但是由于20%截面處的翼型厚、彎度大，因而阻力也相對最大，60%截面處的翼型薄且彎度小，其流動阻力相對最小，因此，40%和60%截面處翼型升阻比基本接近，20%截面處翼型升阻比最低。但幾種翼型總體上而言都具有良好的流動性能，在5 °攻角下60%截面處翼型升阻比達到了25以上，其余兩種翼型均高于45。這也進一步驗證了鳥類翅膀具有高升阻比的特性。

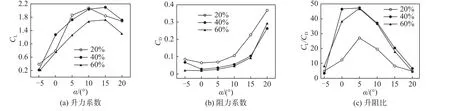
圖4 20%、40%和60%截面處翼型升阻力系數及升阻比(α = 0° ～ 20°, Re = 4 × 105)Fig. 4 Influence of the attack angle on the lift coefficient, drag coefficient and lift-drag ratio of three bionic airfoils (α =0° ～ 20°, Re = 4 × 105)

圖 5（a）、（b）和（c）分別給出了 0°攻角下、進口風速為30 m·s?1時翅翼表面的壓力系數分布，圖中x為x軸方向坐標。壓力系數Cp為

式中：Ps為靜壓；P∞為無窮遠處未受擾動時流體靜壓；v為來流速度。

由圖5中可知，20%和40%截面處翼型的吸力面在0.2倍弦長位置存在局部吸力峰，從翼型前緣到0.4倍弦長范圍，吸力面壓強變化梯度大。相對來說，60%處翼型表面的壓強沿弦長方向分布較為均勻。圖5（d）給出了翼型載荷ΔCp沿弦長的分布，ΔCp為壓力面與吸力面壓力系數之差。可以很清楚地看到，20%、40%和60%截面處翼型的最大載荷均出現在0.2倍弦長位置，值分別為1.94、2.08和1.04，且在較大的弦長范圍內，40%截面處翼型具有較大的載荷，這表明該翼型的升力最大。從圖5（d）還可看出，20%截面處翼型的載荷沿弦向的總體變化梯度?p/?x非常大，而60%截面處翼型的載荷沿弦向變化則較為均勻。20%和60%截面處翼型在最大載荷點前總體變化梯度為16.38和10.97，在最大載荷點后則分別為?85.96和?22.73。顯然，壓強沿翼型表面的急速變化將改變翼型表面附面層厚度發展規律，從而對翼型的氣動特性、附面層內湍流脈動誘導的噪聲產生重要影響。

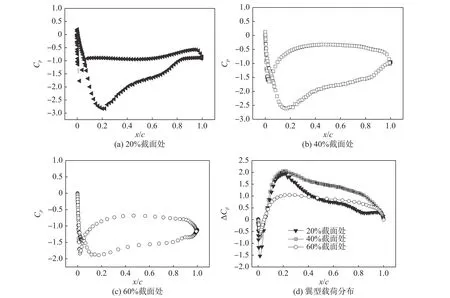
圖5 壓力系數及壓力系數差值分布Fig. 5 Distributions of the pressure coefficient and its difference

圖6給出了0°攻角、進口風速為30 m·s?1、時間為0.04 s時速度云圖和流線圖。由圖中可見，20%截面處翼型的壓力面存在大范圍流動分離，氣流在吸力面x/c = 0.35位置也發生了分離，40%截面處翼型壓力面的分離范圍已明顯減小，而吸力面的分離點位置向后移動至0.67倍弦長處。60%截面處翼型的吸力面附面層基本上沒有發生分離，壓力面在前緣處出現速度分離，但分離范圍小，且在0.45倍弦長位置流體再附。翼型表面的速度場分布特征與圖5給出的壓強及載荷分布特征吻合。

根據渦聲理論［8］，氣動噪聲來源于流場中渦的拉伸和破裂。該理論將氣流輻射噪聲與渦量場相聯系，因此明確流場中渦量的大小、變化和輸運情況，對分析流動聲源的產生機制有十分重要的參考價值。本文根據對各翼型升力及阻力系數的監測結果，將5 000個時間步長的時域數據通過傅里葉變換為頻域信息，得到20%、40%和60%截面處翼型的主頻分別為160、407和977 Hz，則各自周期分別約為0.006 25、0.002 46和0.001 02 s。圖7給出了三個翼型截面在各自的主脈動周期內的渦量圖，間隔為各翼型1/5周期時間。從圖7中可看到：20%截面處翼型在翼型前緣有大量的氣流分離，隨著時間的變化，吸力面上方渦再附后又再次分離，尾緣處也出現穩定的渦脫落，從0.205 40 s至0.206 65 s其壓力面近尾緣處出現了很明顯的渦發展過程；40%截面處翼型在吸力面上方也產生了氣流分離，但其分離點更遠離前緣，也可以很明顯地發現再附及脫落現象，另外，在尾緣及壓力面都有渦產生，尾緣渦脫落現象較為明顯，且強度更大；60%截面處翼型在翼型吸力面邊界層基本依舊附著，沒有很明顯的氣流分離產生，僅在尾緣及前緣下方處出現明顯的渦發展過程。綜合而言，20%截面處翼型渦脫落集中度及強度皆大于其他兩種翼型，40%截面處翼型次之，60%截面處翼型最小，因而僅就渦流噪聲而言，可以預測60%截面處翼型應當為最優，40%截面處翼型次之，20%截面處翼型較差。

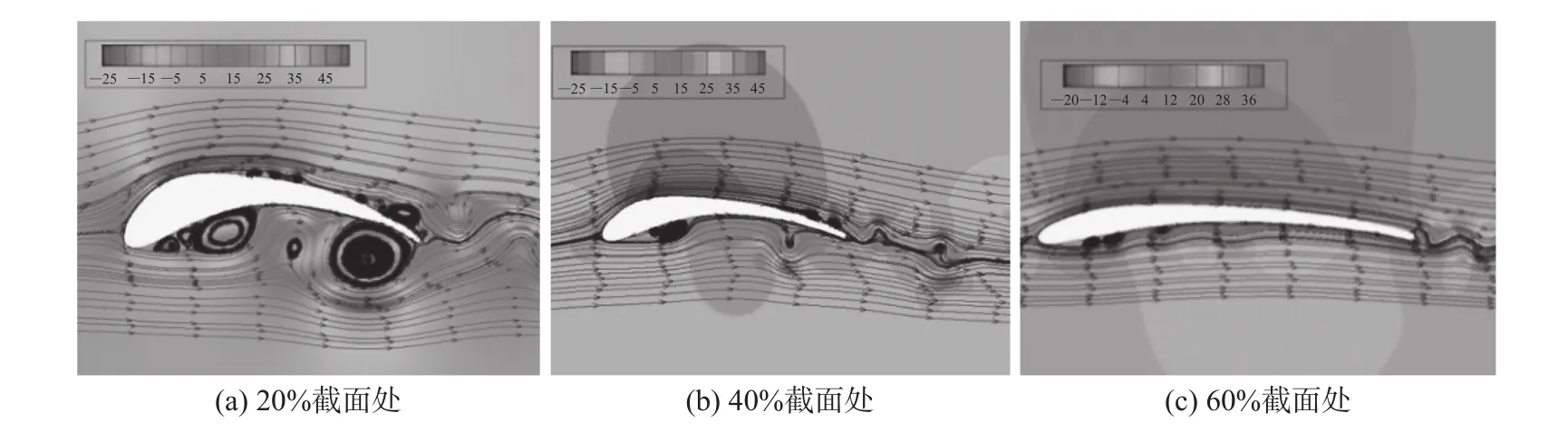
圖6 三個截面處瞬態流場翼型速度云圖和流線圖(t = 0.04 s)Fig. 6 Velocity contours and streamlines of transient flow for three bionic airfoils (t = 0.04 s)

圖7 翼型速度渦量圖Fig. 7 Vorticity and velocity of three bionic airfoils

3.2 翼型繞流聲場分析

為了得到翼型繞流場在各傳播方向上輻射噪聲的能力，在圓心位于翼型前緣、半徑為20倍翼型弦長的圓上布置36個聲壓接收點，分布情況如圖8所示。圖9為三種翼型25 Hz下的聲壓級指向性分布，其中：SPL為聲壓級，單位為dB。圖9表明聲壓級隨輻射方向變化明顯，在上下方和左右方均出現明顯的高、低峰，說明噪聲的主要輻射區在翼型的上下方。可以看出，當進口風速為30 m·s?1、攻角為0°條件下，翼型近壁區渦量最多的20%截面處翼型向周圍輻射的噪聲最大，40%截面處翼型次之，60%處翼型噪聲性能最優。這再次表明渦流噪聲是影響翼型噪聲的重要因素。

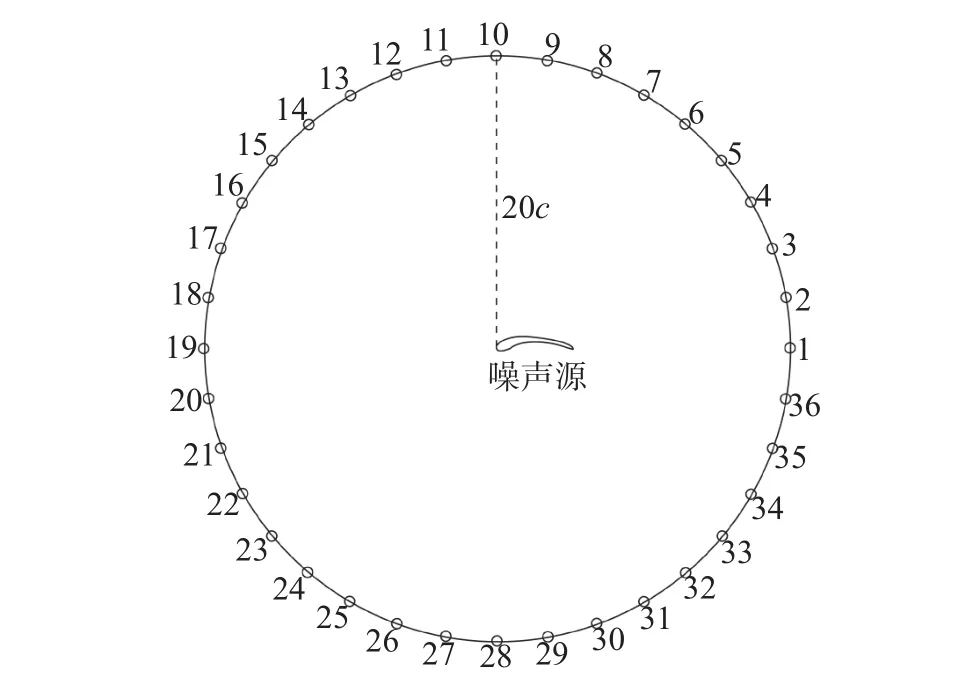
圖8 聲輻射場點分布情況Fig. 8 Field point distribution of the acoustic radiation

圖10給出了長耳鸮翅膀20%、40%和60%截面處翼型的第28個聲壓接收點的聲壓級曲線。從圖中可知，三種翼型的聲壓級頻譜均呈現出明顯的寬頻特性，在0～6 000 Hz范圍內，三種翼型呈現出隨頻率較為相似的變化趨勢。在此范圍內各翼型都有一個聲壓級低峰值，20%截面處翼型低峰值約出現在3 000 Hz處，40%和60%截面處翼型則出現在約4 500 Hz處。三種翼型最高聲壓級皆出現在低頻處，其大小從20%截面處至60%截面處翼型依次下降，分別為85.8、78.6和74.8 dB，對應頻率分別為240、435和 760 Hz。

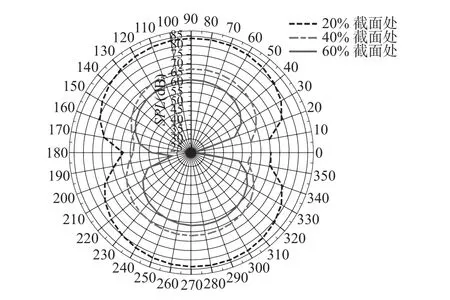
圖9 聲壓級指向性分布Fig. 9 Directional distribution of SPL

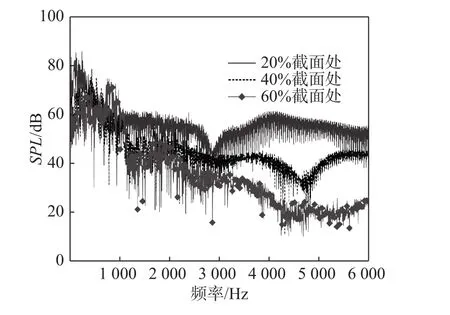
圖10 聲壓級頻譜Fig. 10 SPL spectrum

圖10表明，在0～6 000 Hz范圍內，20%截面處翼型的聲壓最大，40%截面處次之，60%截面處翼型最小。另外，在低于1 000 Hz頻率下各翼型噪聲特性皆比較明顯，三種翼型差距不大，但高于1 000 Hz之后可以明顯地看出，三種翼型噪聲特性隨頻率變化高低有清晰區分。總體而言，20%截面處翼型在各頻率下皆產生了最大噪聲，60%截面處翼型在高頻與低頻下的噪音表現基本都較穩定，噪聲皆為最低，說明該翼型產生的高頻渦流較少，因而此截面擁有最優的噪聲性能。

4 結 論

（1）三種翼型均具有高升阻比特性和良好的流動性能。20%和40%截面處翼型具有較高的升力系數。瞬態流場計算結果顯示，在強烈的逆壓梯度下，這兩種翼型氣流在吸力面前緣后方產生分離，在下游處產生了明顯的不規則渦結構，在脫離尾緣后渦結構發生破碎，并轉化成小尺度湍流；60%截面處翼型阻力系數最小，在升力系數并不出眾的情況下獲得了很高的升阻比。

（2）速度渦量說明三種翼型空氣流動時產生的渦大相徑庭。20%截面處翼型產生最多的渦流，40%截面處翼型次之，60%截面處翼型則有最少的渦流產生。這直接導致了翼型噪聲輻射大小不同，60%截面處翼型噪音最低，20%截面處翼型的則相對最高。

（3）聲壓級指向性分布說明三種翼型的聲源均為偶極子源，并優先向上下方傳播，偶極子圖案偏向性與翼型彎度有關，頻譜圖顯示聲壓級會出現先下降后又逐漸上升的趨勢。這可能是由于隨著流場湍流場的變化，原先產生的頻段中的渦結構逐漸消失，之后隨頻率的增加，高頻渦又開始產生引起的。在低頻段聲壓級達到峰值時有明顯的噪聲特性。三種翼型的噪聲特性產生機理及變化趨勢基本一致，都有各自的高峰與低峰值。聲壓級因各自不同的特殊形態結構有高低之分，其中60%截面處翼型低噪特性更優。