起重機械銷軸連接耳板強度計算的探討
李鵬舉,向金陽,王進峰,王永新
(1.中電投電力工程有限公司,上海 200233;2.山東電力建設第一工程公司,山東 濟南 250131)
1 銷軸連接介紹
銷軸聯接是常用的機械聯接型式之一,在起重機械上得到大量應用,銷軸及連接耳板的強度計算尚無定論,相關文獻的計算方法較多,其結果差異比較大,目前暫無針對性的規范對銷軸連接耳板的強度計算進行明確規定,建議相關組織、機構對此進行試驗研究。
銷軸聯接型式具有承載能力大,拆裝方便等優點,在機械工程中應用廣泛,由銷軸及連接耳板組成,常用的銷軸連接如圖1所示。
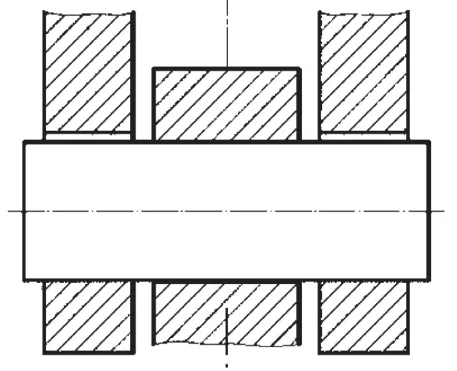
圖1 銷軸連接簡圖
2 強度計算方法
標準規范、設計手冊中給出的強度計算方法有以下幾種可供參考:《塔式起重機設計規范》(GB/T 13752-2017)中關于銷軸連接的計算;《鋼結構設計標準》(GB 50017-2017)中關于銷軸連接的計算;《起重機設計手冊》(第二版,中國鐵道出版社)中關于銷軸連接的計算,此外還有有限元分析法等,下面對主要算法進行介紹和說明。
2.1 算法1
《塔式起重機設計規范》(GB/T 13752-2017)中給出的算法如下,其算法參考ISO 20332-2008新增加內容,包括抗剪承載能力和抗拉承載能力兩部分,即《起重機結構能力驗證》(GB/T 30024-2013)。耳板簡圖如圖2所示。
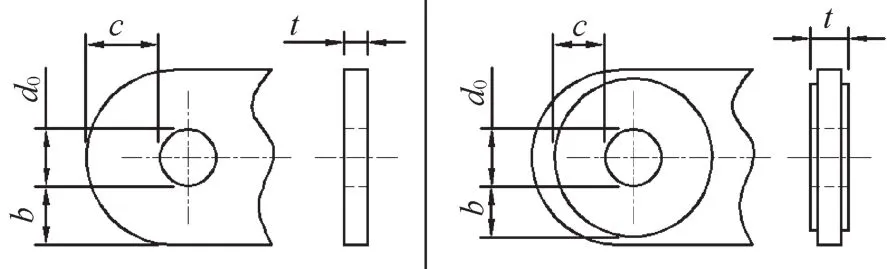
圖2 耳板簡圖一
1)抗剪承載能力銷軸連接的軸心受拉結構件按下式驗算其抗剪承載能力。
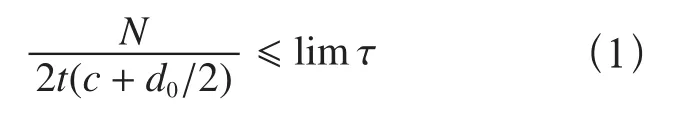
式中:N為作用于連接處的軸向力,b、c、t為幾何尺寸,d0為銷孔直徑,limτ為結構件材料的剪切極限設計應力。
2)抗拉承載能力銷軸連接的軸心受拉結構件應按下驗算其抗拉承載能力。
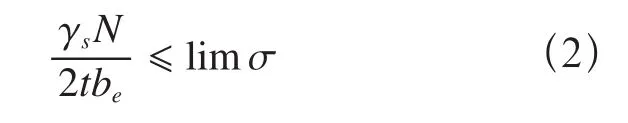
式中:be取(2t+16mm)和b兩者之中的小值,γs為考慮開孔對結構件應力的影響系數,取γs=1.2,limσ為結構件材料的拉壓極限設計應力。
3)構造要求要求c≤b;銷軸和孔之間的配合公差符合GB/T 1800.2-2009的h13/H13或更緊密;在承受變向載荷時,應采用緊密的配合公差;被連接件的剛度應能限制其局部平面外(出平面)變形(表面凹陷)。
2.2 算法2
《鋼結構設計標準》(GB 50017-2017)中給出的算法如下。其算法參考歐標EN 1993-1-8:2005和美標建筑鋼結構規范ANSI/AISC 360-05。考慮凈截面受拉、端部劈開、端部受剪和平面外失穩4種承載力極限狀態。耳板簡圖如圖3所示。
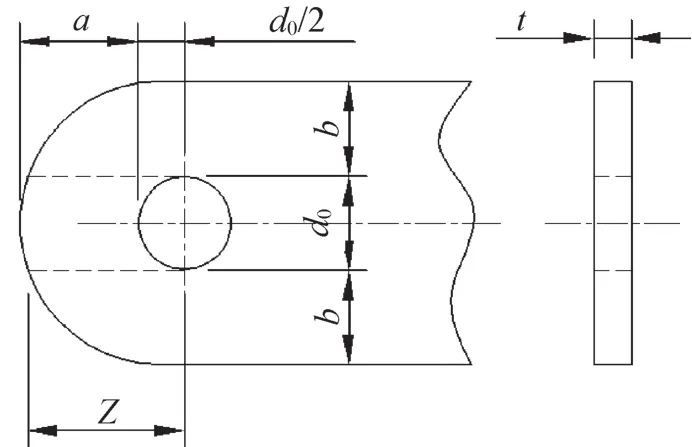
圖3 耳板簡圖二
2.2.1 耳板凈截面處的抗拉強度

2.2.2 耳板端部抗拉(劈開)強度

2.2.3 耳板抗剪強度
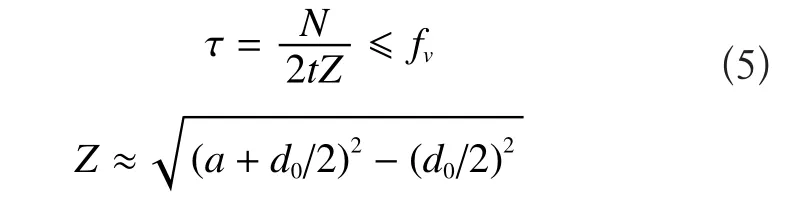
式中:a為順受力方向銷軸孔邊距板邊緣最小距離,t為耳板厚度,b為連接耳板兩側邊緣與銷軸孔邊緣凈距,N為桿件軸向拉力設計值,b1為計算寬度,d0為銷軸孔徑,f為耳板抗拉強度設計值,Z為耳板端部抗剪截面寬度,fv為耳板抗剪強度設計值。
2.2.4 構造要求
要求a≥=2t+16≥b。銷軸孔中心應位于耳板的中心線上,其孔徑與直徑相差不大于1mm;耳板兩側寬厚比b/t不宜大于4;軸孔表面易進行機加工。
2.3 算法3
《起重機設計手冊》(第二版,中國鐵道出版社)中給出的算法如下。其算法根據參考文獻5和6得來,載荷按照余弦規律分布,并根據彈性曲梁理論得出。耳板簡圖如圖4所示。
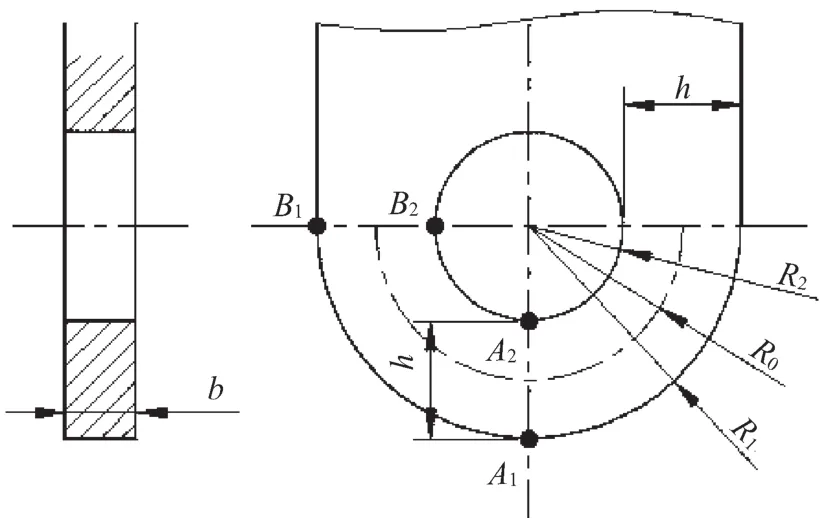
圖4 耳板簡圖三
2.3.1 幾何尺寸
R1、R2、R3為幾何尺寸,
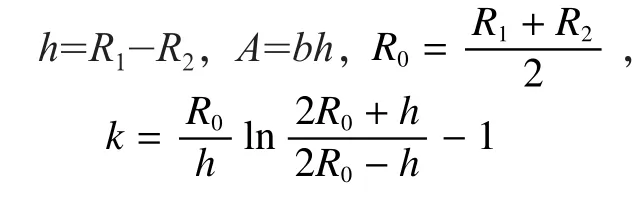
2.3.2 應力大小
P為載荷,內側計算點B2

外側計算點B1
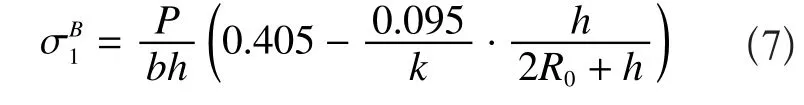
內側計算點A2
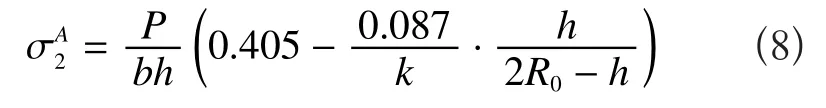
外側計算點A1
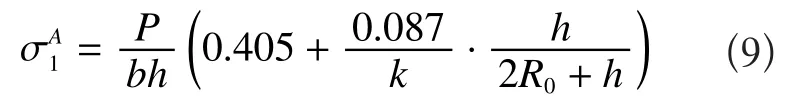
2.4 算法4
有限元分析法,采用SolidWorks三維CAD軟件建立耳板模型,然后導入到Ansys Workbench大型CAE軟件進行分析,選取耳板材料為鋼材,并設置鋼材屬性。對耳板、銷軸和連接板組成的裝配體進行整體分析,如圖5所示。
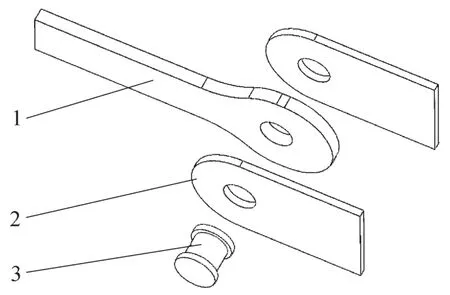
圖5 耳板裝配體示意圖
1)接觸、載荷和約束所有接觸面為摩擦接觸,摩擦系數0.2;在耳板橫截面上添加集中力載荷,方向指向遠離銷軸一側;在連接板橫截面上添加固定約束,如圖6所示。

圖6 耳板載荷和約束
2)網格劃分劃分網格,細化軸孔位置網格大小,如圖7所示。
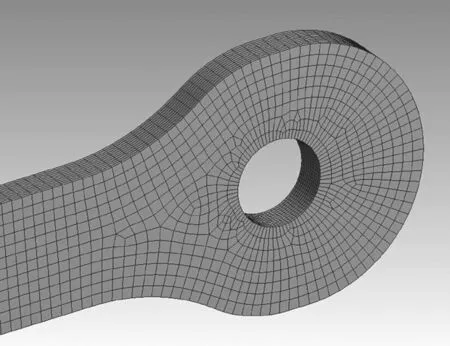
圖7 耳板網格圖
3)應力分布等效應力(Equivalent Stress)大小趨勢及位置分布,如圖8所示。
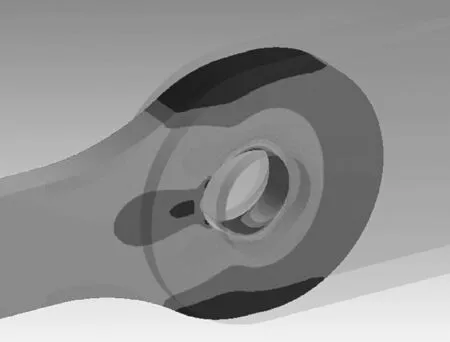
圖8 耳板等效應力分布圖
3 實例對比分析
3.1 材料選擇與強度設計值
選擇材料Q690C,根據低合金高強度結構鋼GB/T 1591-2008中的規定,當σ〉16~40mm時,σs=670N/mm2,σb=855N/mm2,σs/σb≥ 0.7,若按結構件計算,載荷組合A,取S=1.34,則
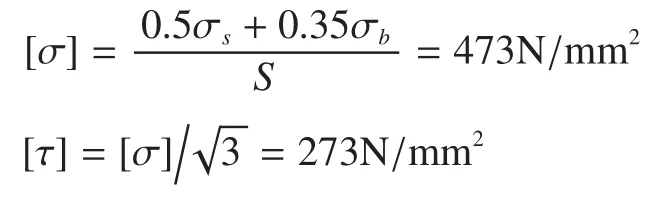
3.2 實例尺寸和載荷
耳板實例尺寸如圖9所示,耳孔承受載荷P=89t,不計動載荷。
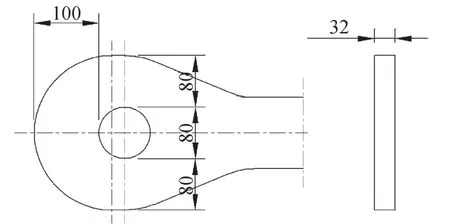
圖9 耳板實例圖
3.3 應力分析
根據以上幾種計算方法,得出各自對應的應力大小和位置,并給出在強度設計值下的極限載荷,見表1。
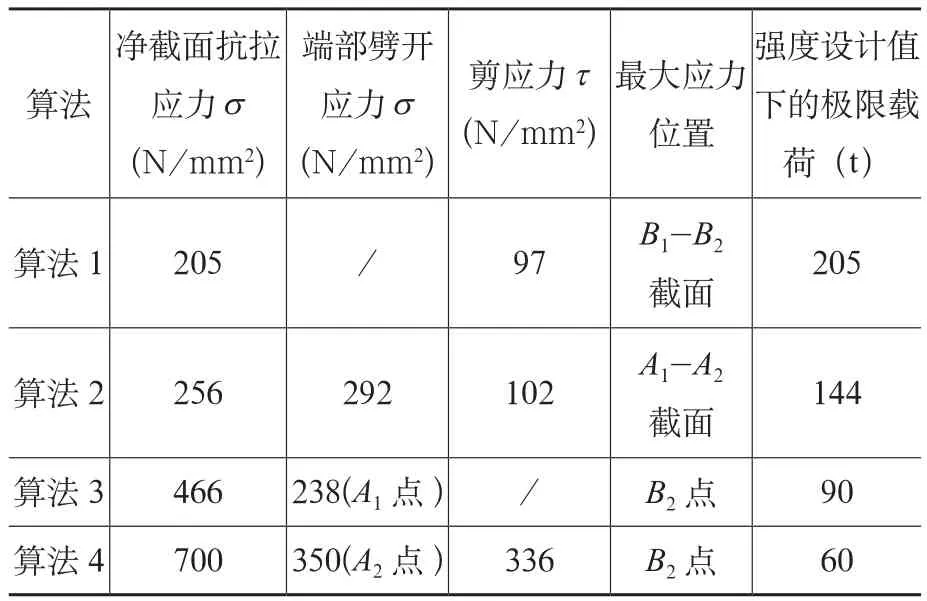
表1 耳板應力大小和位置
由表1可知,算法1和算法2只給出了危險截面的位置,兩種算法的危險截面不同,且都沒有提到合成應力,算法1沒有給出耳板端部劈開位置的應力大小,沒有提及材料是否進入了彈塑性階段,彈性模量是否改變。
算法3和算法4能給出危險點的位置,算法3只給出了正應力,沒有給出剪應力的位置和大小,算法4給出的是等效應力,遵循第四強度理論。
本實例的計算結論滿足算法1、算法2和算法3,算法4(有限元分析法)算得的最大等效應力接近材料的屈服強度。本實例應用于某工程中,經實踐驗證安全可行。
4 結 語
銷軸聯接是起重機械的基本聯接形式,應用廣泛,銷軸連接耳板的安全性至關重要,但目前規范、手冊等文獻給出了多種強度計算方法,其結果差異較大。
算法3[4]為最常用的計算方法,經多年實踐驗證安全可行。
銷軸連接耳板處存在較大的應力集中,隨著載荷的增大,應力超過比例極限,材料進入非線性階段,甚至超過屈服強度,材料彈性模量減小,受力面積擴散,應力得到重新分布。算法4(有限元分析法)能夠計算連接處的集中應力分布情況,當算得的等效應力接近材料的屈服強度且擴散范圍較小時,也可認為耳板是安全的。
算法1和算法2為近期實施標準的新規定,算法1針對的是塔機,算法2側重建筑鋼結構,兩種算法在構造方面提出了嚴格要求,即軸孔需緊密配合。
起重機有別于鋼結構的計算原則是材料在線性的彈性階段,應力不超過比例極限,但實際應用中,耳板局部應力已經進入非線性彈性階段,因此各算法得出的復合應力大小及安全性有待研究。
設計計算中的具體方法和最終取值,應嚴格遵循各行業規程、規范的要求。這類細節問題所反映出的行業難題,說明在基礎問題研究上的缺失和不足,技術人員需要一些安全可靠的正確方法來直接套用。

