基于用戶信任和評分偏置的正則化推薦模型

朱愛云,任曉軍

（濰坊科技學院計算機軟件學院，壽光 262700）

0 引言

隨著網絡和電子商務的快速增長，推薦系統椐據用戶購買或歷史評分信息，能夠快速自動地為用戶提供有用的信息，傳統上推薦系統已經解決了系統對物品評分預測問題。但是，傳統的推薦技術僅僅使用用戶-項目評分信息，為了實現用戶更個性化的推薦結果，開發更智能化的推薦系統，隨著社交網絡的增長，整合社會網絡信息到推薦系統中已引起許多學者的廣泛關注。

傳統的推薦系統[1,2]總是忽視用戶間的社會關系，在現實世界中，人們的社會關系在很大程度上決定了他們的偏好，事實上，當人們面臨多種選擇時，他們可能會通過最好的朋友提供建議，因此為了提供更準確、更個性化的推薦結果，整合用戶間的社會關系到推薦系統中是合理的，基于以上觀點，多種基于信任的推薦系統開始提出,并由此提出了多種信任推薦方法[3-6]，這些方法都是利用單邊信任信息來進一步提高推薦系統的性能，這些方法中顯而易見的弱點是單方面的“信任關系”問題。它不同于那種用戶之間相互合作的“社會關系”。另外，其他弱點也有不可行的假設和弱泛化能力，顯然，基于信任的推薦系統也不太合適。此外，社會網絡的整合從理論上是可以提高傳統推薦系統的性能。因為就預測的準確性而言，朋友關系能夠提高對用戶評分的理解，并且朋友關系也表明在某些方面有共同之處，因此，能夠緩解冷啟動問題[3]。

為了解決以上問題，本文主要關注基于朋友的社會推薦，類似于文獻[8]提出的方法，在矩陣分解中增加用戶、物品偏置信息以及用戶的社會關系，構成正則化推薦模型．通過實驗驗證了增加用戶、項目的評分偏置和用戶的社會關系能提高推薦的準確度，并且也能應用于現實生活中的大規模數據集中。因為在現實生活中，人們經常在購買一種產品或消費一種服務前，借助于他們在社交網絡中的朋友的建議。從社會學和心理學研究發現也表明,人們傾向于結交跟自己的興趣相似的人，由于穩定和持久的社會綁定,人們更愿意與他們的朋友分享他們的個人觀點,因此通常在陌生人、供應商和朋友中首先會選擇他們朋友的推薦。

1 相關工作

傳統推薦方法主要有三類：協同過濾[2,9,10]、內容過濾以及混合過濾[1]。其中協同過濾是最普遍和最成功的方法。

通常，協同過濾推薦方法分為基于模型[9]方法和基于內存[2]方法，基于內存的方法從評分矩陣中查找與當前用戶偏好最相似的用戶，是一種啟發式的評分預測。基于模型的方法使用評分集合來學習，然后用來進行評級預測。

傳統的推薦方法已發展的很成熟，但是它們都是假設用戶是獨立的，沒有考慮用戶間的朋友關系，基于以上考慮，許多研究者提出了許多信任推薦方法[4-7,11,14]并廣泛應用在學術和工業領域。但是推薦進程仍與真實世界的推薦過程不一致，因此,他們提出了另一種集成方法，在同一時間,通過考慮用戶的喜好和受信任的用戶的喜好來計算用戶的評分。實驗表明，該方法是可行的,能夠開發更好的推薦模型。基于信任的推薦系統已被證明是有效的，并取得了巨大的進步。然而,通過分析，它們也有幾個固有的局限性和弱點需要解決。

近年來，在工業界和學術界如何利用社會網絡信息已成為一個研究熱點。通過結合社會網絡信息能夠影響個人在網上的行為，如用戶間的互動、標簽信息等能提高推薦系統的性能。文獻[12]提出了一個融合社會朋友信息的個性化推薦概率模型，并在真實數據集上驗證了用戶與他的朋友在許多方面有相似的偏好。文獻[8]提出了一種基于概率矩陣分解的社會正則化和因子分解法，該方法通過利用網絡信息提高了數據稀疏性問題和冷啟動問題。文獻[8,13]整合朋友關系來提高推薦系統的性能。并且很多社會推薦技術都是基于矩陣分解來解決評分預測問題[8,13,16],矩陣分解方法是是目前比較成功的推薦方法，它將評分/購買矩陣分解成低維的用戶矩陣和項目矩陣，用戶和項目特征向量的點積說明了給定用戶對項目的偏好程度。假定用戶u對物品i的評分用ru,i表示，用戶u對物品i的預測評分用r^u,i表示，其中r^u,i是由用戶特征向量 pu和項目特征向量qi的內積得到。

即：

但是，在實際的推薦系統中，有的用戶往往熱衷于給用戶打分高，有的項目也給予了很高的評分，因此預測評分[15]為：

其中，bu為用戶u的偏置評分，bi為項目i的偏置評分，e為數據集中所有評分的平均評分。

因此，目標函數為：

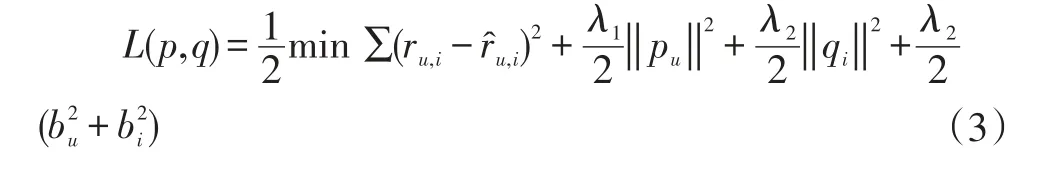
2 融合社會關系和評分偏置的正則化推薦模型

隨著社交媒體的日益普及，使得越來越多的在線用戶參與在線活動，從而產生了更為豐富的社會關系。在社會推薦系統中,除了用戶的評分信息外，還有用戶之間的社會關系，社會關系的有效性為推薦系統提供了一個獨立的資源，也為獨特的社會推薦的屬性帶來了新的機遇。本文將結合用戶的社會網絡關系來提高推薦系統性能，假設用戶有不同類型的社會關系（家人、朋友、同事、同學等），如果兩個人建立一種社會關系，那么就說他們存在一種社會關系。一種社會關系可能對稱也可能不對稱。需要從以下方面定義這種關系。因此，在這一部分描述了本文提出的方法。

定義1假定U={u1,u2,u3,…,un}是一個用戶集，I={i1,i2,i3,…,im}是一個項目集,則社會評分網絡SRN=＜U,I,?,φ＞ 是 一 個 四 元 組,其 中 φ∶U×I→R+∪{"*"}是一個評分函數，用一個真實的值關聯著一個用戶ux∈U和一個項目in∈I，即用戶u對項目i的評分為ru,i，否則用“*”表示。

φ∶U×U→{0,1}是一個社會函數，即一對用戶ux,uy∈U存在一種社會關系，則函數值為1，否則為0。這種社會關系對一些用戶對(ux,uy)通常是不對稱的，也就是 φ(ux,uy)≠φ(uy,ux)。

定義2 假定SRN=＜U,I,?,φ＞是一個社會評分網絡，且用戶ux∈U,用戶ux與他的鄰居Nx存在一種社會關系Nx={uy∈U∶φ(ux,uy)=1}。

在現實生活中,我們通常咨詢我們熟悉的朋友，因為他們熟悉我們的品味，所以來自社會信息的熟悉度和相似度證據表明包含評分信息的社會信息能夠潛在的提高推薦性能，因此，本文中在文獻[9,14]方法基礎上增加了用戶的直接朋友關系作為正則化條件構建模型。猜想如果兩個用戶u,w是直接朋友關系，那么他們應該在特征空間中會映射成一個非常接近的點，換言之假設有三個用戶u,w,x，分別映射到特征空間中的點為 pu,pw,px，但如果只有u,w是朋友，那么 pu,pw之間的距離可能要小于點 puk到點u的距離，事實上，如果一個用戶pu在潛在特征空間中很接近于他的直接朋友 pw，那么用戶 pu的觀點與他的朋友 pw的觀點將會是相似的，為此從數學的觀點考慮在潛在的特征空間中用戶u,w之間的距離為||pu-pw||，其中||·||是歐幾里德距離的范式，用N(u)表示用戶u的直接朋友的最近

鄰居，我們的目的是使盡可能的最小，因此公式（6）增加懲罰因子改為如下公式：

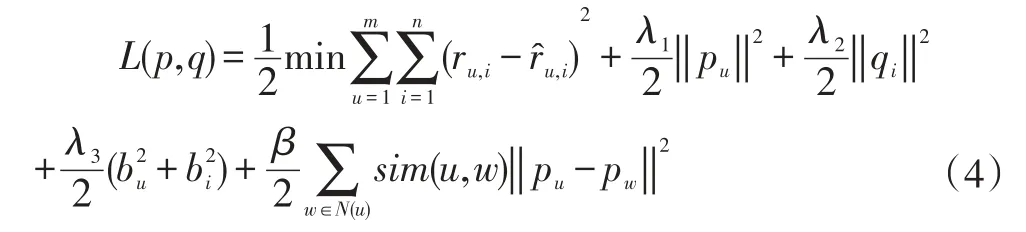
本文稱之為融合社會關系和評分偏置信息的正則化方法（簡稱 Social B-SVD）。其中，（ β,λ1,λ2,λ3均為＞0的常數）用于調整過擬合，sim(u,w)表示用戶u與他的直接朋友w的相似度，我們用皮爾遜相關系數（PCC）即可求出相似度：

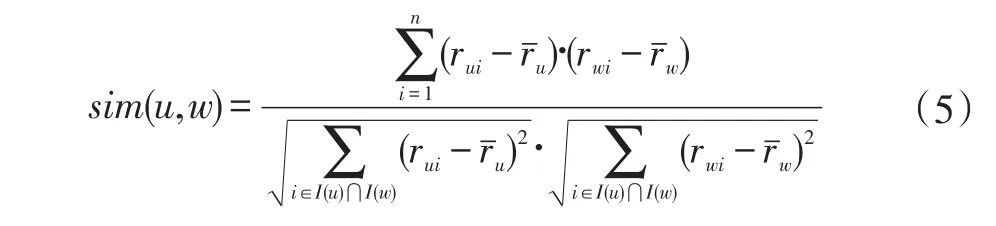
其中，相似度sim(u,w)值越大，表明特征向量pu,pw之間的距離越小，也就表明他們之間有更加相似的偏好，反之，相似度越小，表明特征向量之間的距離越大。其中rˉu是用戶u的平均評分，從這個相似度公式中得到 sim(u,w)∈[-1,1]，為了約束它的范圍[0,1]，采用一個映射函數 f(x)=(x+1)/2。

為了解決這個最優化問題，首先需要對目標函數中的參數puk,qik,bu,bi分別求偏導。

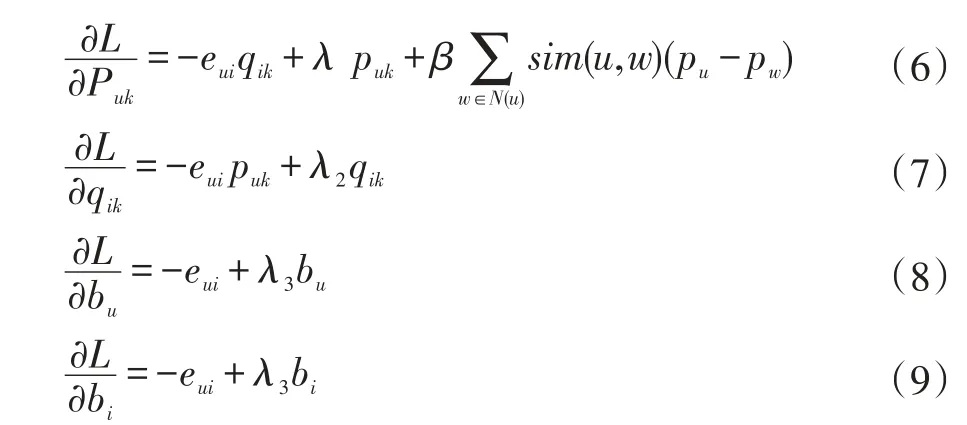
然后利用隨機梯度下降法，沿最速下降方向遞推得到如下公式：

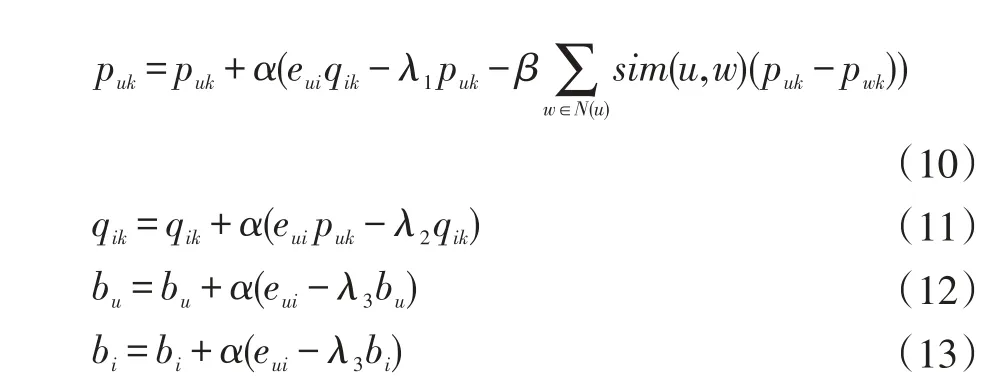
其中，α為學習速率,并按每次迭代縮減為0.9倍的速度遞減。

下面是具體的算法：

算法：融合社會關系的矩陣分解（SocialB-SVD），用戶對項目的分rui,需要分解的特征維數 k

輸入：用戶數m，項目數n，迭代次數為T。

輸出：潛在用戶特征矩陣 U和潛在項目特征矩陣V。

開始

隨機初始化：用戶特征矩陣 U，項目特征矩陣 V,每個用戶u的朋友特征矩陣 pw，每個用戶的偏置向量bu和每個項目i的偏置向量bi。

3 實驗結果

3.1 數據集和結果分析

在本文中，我們采用Flixster數據集作為此實驗數據集，此數據集包含了用戶間的社會網絡和用戶評分，用戶間的社會網絡是無向的，評分值介于[0.5,5.0]之間,且步長為0.5。

在實驗中，我們從數據集中隨機抽取了80%的評分數據作為訓練集，剩余20%作為測試集，并且從社交網絡關系數據中抽取了20000個朋友作為訓練集，學習速率參數α與正則化參數λ1,λ2,λ3,β通過交叉驗證決定。本文采用α=0.0002,λ1=0.003，λ2=0.002，λ3=0.004,β=0.2進行實驗。并且采用均方根誤差（RMSE）和平均絕對誤差（MAE）來評價預測準確度。

取特征維數為k=10,和k=30，迭代次數為30時對比了以下這5種算法的預測準確度。

（1）ItemMean:此方法使用每個項目的平均值來預測缺失值。

（2）SVD:是最傳統的矩陣分解推薦算法，已廣泛應用于推薦系統中,但它忽視了用戶間的社會關系。

（3）Bias_SVD:是 Koren[16]提出的一種推薦方法，該方法使用戶的偏置信息、項目的偏置信息整合到推薦系統中，提高了推薦性能。

（4）Social_SVD:是Ma[8]提出的一種信任感知推薦方法，利用矩陣分解融合用戶和她朋友的品味構建正則化模型。

（5）SVD++:這種方法是 Koren[15]提出的，他考慮了用戶和項目的偏見值對評分的影響，也融合了用戶評分的顯式和隱式影響。

本實驗中，特征維數設置為k=10和30，針對所有用戶做了實驗對比，實驗結果如表1所示，不論k=10,30，與表中其他的方法相比較，我們所提出的Social BSVD方法的性能是最好的（MAE或RMSE值最小），雖然相對提高的比例很小，但是也表明融合社會網絡信息的Social B-SVD方法會大大提高推薦系統的性能。

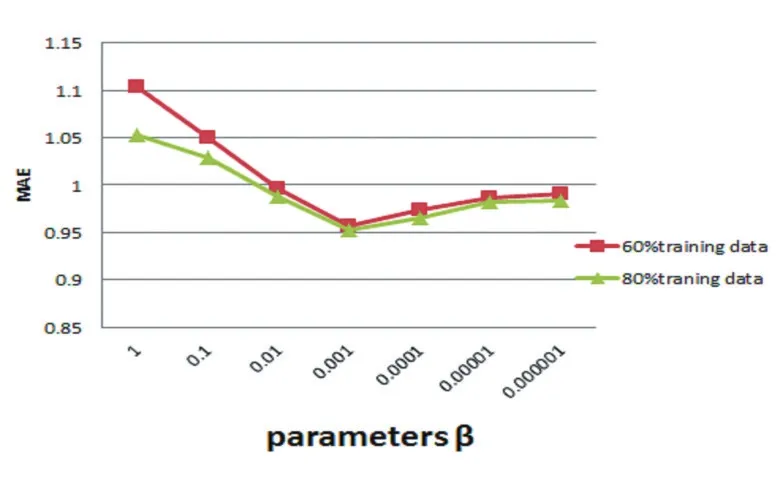
圖1 參數β的影響（k=10）

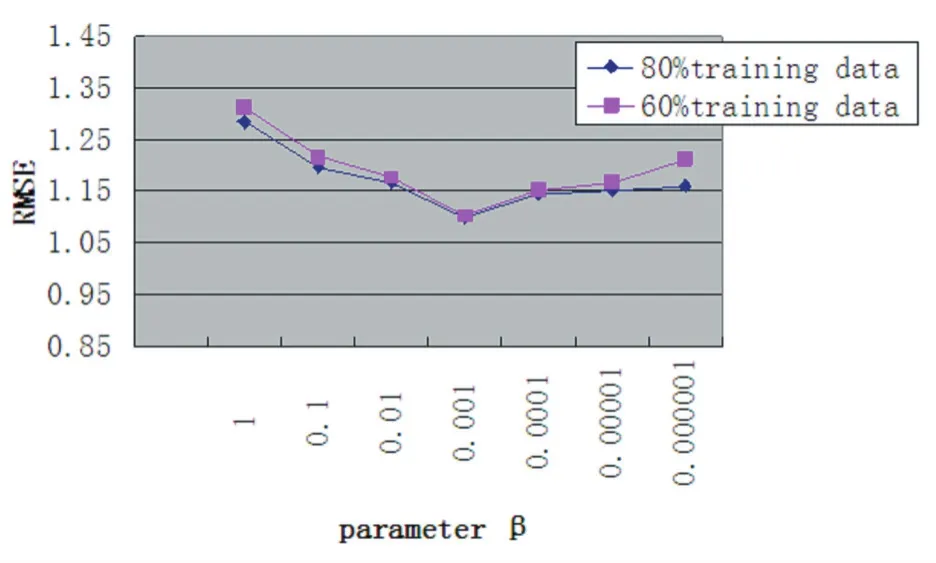
圖2 參數β的影響（k=10）

3.2 參數β的影響

在本文中參數β對預測準確度起著重要的作用，它表示到底應該結合多少社交網絡信息才能達到最佳狀態。在極端的情況下，如果我們用一個很小的β值，它表明僅僅使用用戶自己的品味來做出推薦，相反，我們如果用一個很大的β值，那么社會網絡信息在學習過程中就占支配地位。但在許多情況下，我們都不想設置這些極端值，從圖1，圖2中我們看到不管用哪種數據集，隨著β值的增加MAE/RMSE值開始在減少，但當達到某一個閾值（0.001在Flixster數據集上）時，隨著β值的繼續增加MAE/RMSE又開始增加，這個拐點的存在說明融合社交網絡信息到矩陣分解中進行推薦遠遠好于單純使用用戶項目評分或單純使用社交網絡信息。

表1 Flixster數據集中預測準確度的比較

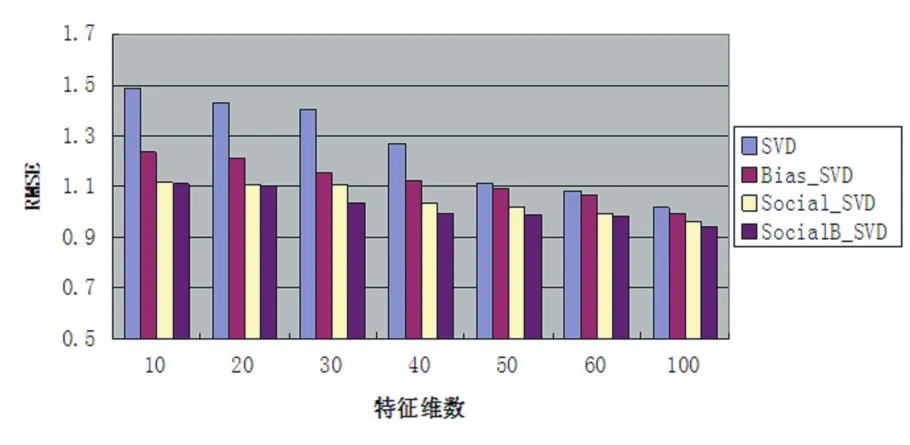
圖3 特征維數k對RMSE的影響

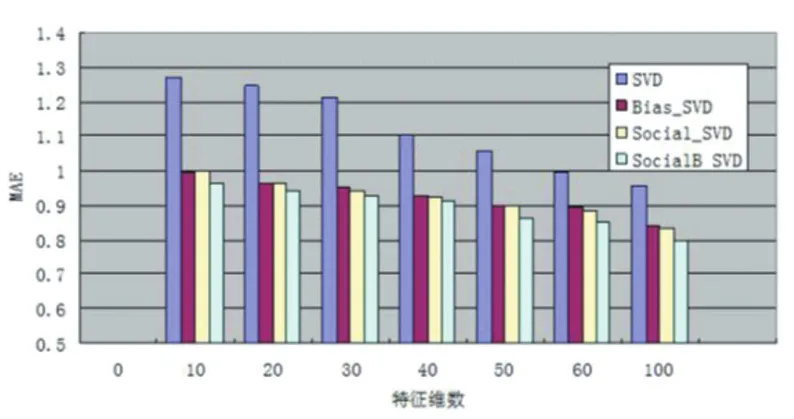
圖4 特征維數k對MAE的影響

3.3 特征維數k 的影響

在本文中通過實驗驗證特征維數k對預測準確度影響較大，我們選擇k=10,20,30,40,50,60,100進行模型訓練。從圖3、圖4可以看到，在我們提出的方法中，隨著特征維數k值的增加，MAE/RMSE值開始下降很快，但是隨著k值的增加MAE/RMSE下降速度變慢（由圖 3、圖 4得到 k值從 60到100，MAE值從 0.8451下降到0.7906，RMSE值從0.9842下降到0.9439），也從側面驗證了算法每次計算出的都是最顯著的特征向量。

4 結語

本文在傳統的奇異值（SVD）矩陣分解模型中融合了社交網絡中的直接朋友關系和用戶評分偏置信息作為輔助信息，設計了基于社交網絡信息的矩陣分解算法。實驗表明，本文提出的算法具有較好的預測效果，其性能明顯優于相比較的相關算法。

[1]Adomavicius,G.,Tuzhilin,A..Toward the Next Generation of Recommender Systems:a Survey of the State-of-the-Art and Possible Extensions.IEEE Trans.Knowl.Data Eng，2005，17（6）：734-749

[2]Bellogin,A.,Castells,P.,Cantador,I..Improving Memory-Based Collaborative Filtering by Neighbour Selection Based on User Preference Overlap.In:Proceedings of the 10th Conference on Open Research Areas in Information Retrieval,Lisbon,Portugal,2013，May 15-17：145-148.

[3]Jamali,M.,Ester,M..A Matrix Factorization Technique with Trust Propagation for Recommendation in Social Networks.In:Proceedings of the 4th ACM Conference on Recommender Systems,Barcelona,Spain,2010，September 26-30：135-142.

[4]Ozsoy,M.G.,Polat,F..Trust Based Recommendation Systems.In:Proceedings of the 2013 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining（ASONAM'13）,Niagara,ON,Canada,2013，August 25-29：1267-1274.

[5]Massa,P.,Avesani,P..Trust metrics in recommender systems.Comput.Soc.Trust,2009:259-285.

[6]Nazemian,A.,Gholami,H.,Taghiyareh,F..An Improved Model of Trustaware Recommender Systems Using Distrust Metric.In:Proceedings of the IEEE/ACM International Conference on Advances in Social,2012.

[7]Ma,H.,Yang,H.,Lyu,M.R.,King,I..SoRec:Social Recommendation Using Probabilistic Matrix Factorization.In:Proceedings of the 17th ACM Conference on Information and Knowledge Management,Napa Valley,California,USA,2008，October 26-30：931-940.

[8]Ma H,Zhou D Y,Liu C.Recommender Systems Withsocial Regularization[C].In Proceedings of the 4th ACM International Conference on Web Search and Data Mining,2011,287-296.

[9]Bergner,Y.,Droschler,S.,Kortemeyer,G.,et al..Model-based Collaborative Filtering Analysis of Student Response Data:Machine-Learning Item Response In:Proceedings of the 5th International Conference on Educational Data Mining,Chania,Greece,,2012,June 19-21:95-102.

[10]Gunes,I.,Bilge,A.,Polat,H..Shilling Attacks Against Memory-based Privacy-Preserving Recommendation Algorithms.Internet Inf.Syst,2013,7（5）：1272-1290.

[11]Nazemian,A.,Gholami,H.,Taghiyareh,F..An Improved Model of Trustaware Recommender Systems Using Distrust Metric.In:Proceedings of the 2012 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining,Istanbul,Turkey,2012，August 26-29：1079-1084.

[12]He,J.,Chu,W.,PhD Dissertation.A Social Network-Based Recommender System（SNRS）.University of California at Los Angeles,CA,USA,2010.

[13]Wang,X.,Huang,W..Research on Social Regularization-Based Recommender Algorithm.Comput.Mod.,2014，1：77-80.

[14]王瑞琴，蔣云良，李一嘯.一種基于多元社交信任的協同過濾推薦算法[J].計算機研究與發展，2016,53（6）：1389-1399

[15]Koren Y,R BeII,C Volinsky.Matrix Factorization Techniques for Recommender Systems[J].Compute Socety,2009,42（8）:30-37.

[16]Koren Y.Factor in the neighbors Scalable and Accurate Collaborative Filtering[J].ACM Transactions on Knowledge Discovery from Data（TKDD）,2010,1（4）:1-11.