兩柱掩護(hù)式液壓支架承載特性研究

韓進(jìn)軍， 王 彪

（1.潞安集團(tuán)常村煤礦， 山西 屯留 046100； 2.潞安集團(tuán)安監(jiān)局， 山西 襄垣 046299）

引言

在以往研究中只是單一分析支架理想水平位時(shí)的受力狀況，且忽略掩護(hù)梁受力對(duì)頂梁合力作用點(diǎn)位置及大小造成的影響，然而實(shí)際工況中，支架姿態(tài)往往會(huì)隨圍巖運(yùn)移及周期來(lái)壓等地質(zhì)現(xiàn)象的發(fā)生而改變，掩護(hù)梁也會(huì)承受后部垮落矸石的壓力，上述研究方法不能準(zhǔn)確求出支架不同姿態(tài)下頂梁合力作用點(diǎn)的位置及大小，繼而無(wú)法確定當(dāng)前姿態(tài)下支架頂梁合力作用點(diǎn)的合理受力區(qū)間，不能提出有效的姿態(tài)調(diào)整策略。因此，為了及時(shí)了解支架與圍巖相互作用關(guān)系，維護(hù)圍巖穩(wěn)定，保證工作面設(shè)備的安全生產(chǎn)，有必要對(duì)支架不同姿態(tài)下的頂梁承載特性開(kāi)展深入研究[1]。

1 液壓支架受力分析

1.1 支架平面力學(xué)模型建立

本文構(gòu)建了支架平面力學(xué)模型，并充分考慮掩護(hù)梁受力對(duì)支架頂梁合力作用點(diǎn)帶來(lái)的影響，該模型可描述兩柱掩護(hù)式液壓支架在縱向平面內(nèi)任意姿態(tài)下的受力狀況，如圖1所示[2]。

圖1 支架平面受力圖

其中：O為參考坐標(biāo)點(diǎn)，O1為支架四連桿機(jī)構(gòu)運(yùn)動(dòng)瞬心，G為頂梁與掩護(hù)梁鉸接點(diǎn)，Q為垂直于頂梁的載荷（即支架頂梁承載力）、XQ為G點(diǎn)到承載力作用線的距離，Qf為頂板對(duì)支架的摩擦阻力（摩擦系數(shù)f一般為0.1～0.3），P為立柱的工作力，PE為平衡千斤頂?shù)墓ぷ髯枇Γó?dāng)活塞腔受壓時(shí)PE取“＋”，當(dāng)活塞桿腔受壓時(shí)PE取“－”），r1為O1點(diǎn)到G點(diǎn)所在直線距離，r2為O1點(diǎn)到頂梁所在直線距離，r3為O1點(diǎn)到立柱所在直線距離，r4為O1點(diǎn)到平衡千斤頂所在直線距離，r5為G點(diǎn)到立柱所在直線距離，r6為G點(diǎn)到平衡千斤頂所在直線距離，F(xiàn)為掩護(hù)梁所承受作用載荷（分解為水平方向FX和豎直方向FY），LF為掩護(hù)梁作用載荷到下鉸點(diǎn)的距離，F(xiàn)1、F2分別為前連桿和后連桿所受作用力，α、β、γ分別為頂梁、后連桿、底座與水平面的夾角，H、X、Y及各鉸接點(diǎn)坐標(biāo)為因變量，構(gòu)建如下運(yùn)動(dòng)方程組，其中K1～K18為中間變量，其中各力與角度的正方向如圖1所示。

1.2 合力作用點(diǎn)計(jì)算

本文對(duì)支架的運(yùn)動(dòng)學(xué)特性進(jìn)行了分析，并推導(dǎo)出了基于頂梁、底座、后連桿三傾角傳感器的兩柱掩護(hù)式液壓支架姿態(tài)算法，利用該算法可對(duì)A、B、D、E點(diǎn)坐標(biāo)進(jìn)行求解，通過(guò)計(jì)算其結(jié)果表示如下[3]：

作BE與AD的延長(zhǎng)線使其交于O1點(diǎn)，如圖1所示，則依據(jù)理論力學(xué)相關(guān)定理可知O1點(diǎn)為支架四連桿機(jī)構(gòu)的運(yùn)動(dòng)瞬心，在已知A、B、D、E點(diǎn)坐標(biāo)前提下，可進(jìn)一步求解瞬心O1點(diǎn)坐標(biāo)，其結(jié)果表示如下：

其中：

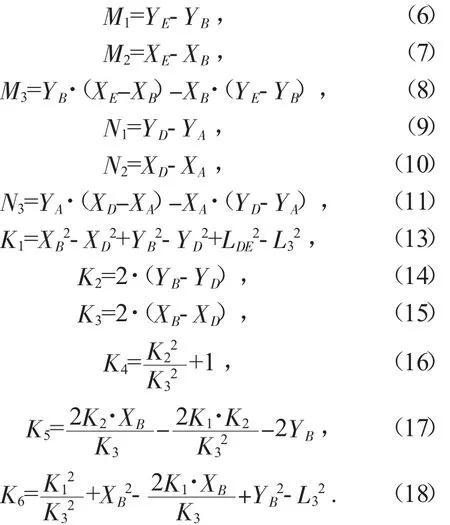
1）若不考慮掩護(hù)梁受力，則：

以頂梁、掩護(hù)梁為隔離體，對(duì)瞬心O1點(diǎn)取力矩平衡方程：

以頂梁為隔離體，對(duì)G點(diǎn)取力矩平衡方程：

聯(lián)立求解可得：

式中：f為頂板與頂梁之間的摩擦系數(shù)，取0.1～0.3。

2）若考慮掩護(hù)梁受力，則：

以頂梁、掩護(hù)梁為隔離體，對(duì)瞬心O1點(diǎn)取力矩平衡方程：

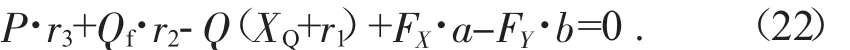
a為GX作用點(diǎn)與瞬心O1之間的距離，其值可表示為：

b為作用點(diǎn)GY與瞬心O1之間的距離，其值可表示為：

以頂梁為隔離體，對(duì)G點(diǎn)取力矩平衡方程為：

聯(lián)立求解可得：

通過(guò)上述計(jì)算可確定支架在任意姿態(tài)下頂梁所承受載荷的大小及作用位置，為對(duì)支架姿態(tài)與頂梁承載特性關(guān)系的進(jìn)一步分析提供了研究基礎(chǔ)。

2 液壓支架承載特性分析

本節(jié)將利用matlab軟件以掩護(hù)梁受力、支架高度、頂梁傾角三個(gè)影響因素為方向?qū)χЪ艹休d特性的變化加以論述。

2.1 掩護(hù)梁受力對(duì)支架承載性能的影響分析

假設(shè)上頁(yè)圖 1中 α、β、γ 分別等于 0°、60°、0°，將支架合力作用點(diǎn)計(jì)算公式編寫(xiě)為matlab可執(zhí)行代碼，利用繪圖功能繪制不同受力狀態(tài)下支架的承載性能曲線。

將不考慮掩護(hù)梁受力與不考慮掩護(hù)梁受力兩曲線疊加分析，如圖2所示。

圖2 掩護(hù)梁受力對(duì)支架承載性能影響曲線

對(duì)考慮掩護(hù)梁受力及不考慮掩護(hù)梁受力兩種狀態(tài)時(shí)支架承載特曲線做比較，可知當(dāng)掩護(hù)梁承受一定載荷時(shí)，支架承載特性曲線向左上方偏移，頂梁承受外部載荷及平衡千斤頂受拉工作區(qū)的承載能力均略有增加，但平衡千斤頂受壓工作區(qū)的承載能力略有下降，支架易出現(xiàn)低頭現(xiàn)象。因此，在實(shí)際生產(chǎn)中，當(dāng)支架掩護(hù)梁承受載荷時(shí)，應(yīng)避免支架低頭，并對(duì)已經(jīng)低頭的支架活塞腔及時(shí)補(bǔ)壓或進(jìn)行其他輔助措施，提高支架前端的支護(hù)能力。

2.2 支架高度對(duì)支架承載性能的影響分析

假設(shè)支架頂梁、底座處于水平狀態(tài)，對(duì)前述matlab可執(zhí)行代碼進(jìn)行修改，繪制支架處于不同高度時(shí)的支架承載特性曲線。

將三組曲線疊加分析，如下頁(yè)圖3所示。

圖3 不同支架高度對(duì)支架承載性能影響曲線

通過(guò)對(duì)上圖中三組曲線作對(duì)比分析可知，該型支架在頂梁底座水平，由低位升至高位的過(guò)程中，支架承載性能曲線向左上方移動(dòng)，平衡千斤頂受拉工作區(qū)變化較小可忽略不計(jì)而受壓工作區(qū)承載能力則顯著提升，立柱工作區(qū)變長(zhǎng)且承受外部載荷能力增加。由此可見(jiàn)，該型支架在實(shí)際工作中，處于高位態(tài)時(shí)的工作姿態(tài)可以提升支架的承載能力，增大立柱工作區(qū)間，提高支架穩(wěn)定性，同時(shí)也可提高支架前端的支護(hù)能力，有利于防止低頭現(xiàn)象的出現(xiàn)。

2.3 頂梁傾角對(duì)支架承載性能的影響分析

假設(shè)支架底座水平，立柱伸長(zhǎng)量為固定值，對(duì)前述matlab可執(zhí)行代碼進(jìn)行修改，繪制支架頂梁不同傾角時(shí)的支架承載特性曲線。

將三組曲線疊加分析，如圖4所示。

對(duì)比圖中三條曲線可知，支架立柱伸長(zhǎng)量為定值、底座水平時(shí)，支架承載性能會(huì)隨頂梁傾角的改變而發(fā)生變化。當(dāng)頂梁呈現(xiàn)抬頭狀態(tài)時(shí)，支架承載性能曲線向右上方移動(dòng)，支架承受外載能力增強(qiáng)，立柱主平衡區(qū)向頂梁后端移動(dòng)，平衡千斤頂受拉工作區(qū)即頂梁后端承載能力增強(qiáng)，有利于阻止頂梁的進(jìn)一步抬頭；當(dāng)頂梁呈現(xiàn)低頭狀態(tài)時(shí)，支架承載性能曲線向左下方移動(dòng)，支架承受外載能力略有降低，立柱主平衡區(qū)向頂梁前端移動(dòng)，但平衡千斤頂受壓工作區(qū)即頂梁前端承載能力增強(qiáng)，有利于阻止頂梁的進(jìn)一步低頭。

圖4 頂梁支架承載性能曲線

3 結(jié)論

通過(guò)從掩護(hù)梁受力、支架高度、頂梁傾角三個(gè)方面對(duì)影響支架承載性能的因素進(jìn)行直觀的圖形曲線分析，可知三者對(duì)支架的承載性能有著重要的影響。在實(shí)際工況中應(yīng)充分考慮掩護(hù)梁受力、支架姿態(tài)及工作高度，對(duì)已處于平衡千斤頂最大受拉及受壓極限狀態(tài)的支架做調(diào)整，使其盡可能工作于立柱主平衡區(qū)，提高支架承載能力及穩(wěn)定性。