磁性斯格明子的賽道存儲?
梁雪 趙莉 邱雷 李雙 丁麗紅 豐友華 張溪超 周艷 趙國平3)
1)(四川師范大學物理與電子工程學院,成都 610101)
2)(香港中文大學(深圳)理工學院,深圳 518172)
3)(山西先進永磁材料與技術協同創新中心,臨汾 041004)
磁性斯格明子是拓撲穩定的自旋結構,它的尺寸小,驅動電流閾值小,被廣泛認為是下一代磁性存儲的基本單元.斯格明子的主要優勢在于它奇特的動力學性質,特別是它能夠與傳導電子相互作用,在低電流密度驅動下可以在賽道上穩定地運動.本文結合磁性斯格明子賽道存儲的最新研究成果,對斯格明子在賽道上的寫入、驅動和讀出三個方面進行了較為詳細的綜述.重點介紹了注入自旋極化電流這一最常見的驅動方法,分析了斯格明子在賽道上的堵塞和湮沒現象,探討了斯格明子霍爾效應及其可能造成信號丟失的危害和相關的解決方法,并在此基礎上詳細介紹了幾種斯格明子塞道存儲的優化設計方案.最后總結了磁性斯格明子賽道存儲面臨的一些挑戰.
1 引 言
斯格明子最早由英國粒子物理學家Skyrme[1]提出,用于描述介子領域中的局域化的準粒子結構.此后,這一物理概念也用于很多其他領域,比如:核物理、量子霍爾體系、液晶以及超冷原子等[2,3].斯格明子是一種受拓撲保護的結構,可以由一個拓撲整數來表征,其拓撲數不會在場的連續形變下而發生改變.有趣的是,這種非拓撲平庸的準粒子也可以穩定地存在于手性磁體中,即磁性斯格明子[3].有了這些開創性的理論工作[4?7],此后不斷涌現出大量研究磁性斯格明子的實驗工作.2009年,Mühlbauer等[8]通過小角度中子散射實驗,在MnSi材料中首次證實了斯格明子晶體(skyrmion lattice)的存在;Yu等[9]利用洛倫茲透射電子顯微鏡(Lorentz transmission electron microscopy,LTEM)在Fe1?xCoxSi首次得到真實空間中斯格明子的成像;Heinze[10]在Ir表面生長的Fe單原子層中用自旋極化掃描隧道顯微鏡(spin-polarized scanning tunneling microscopy,SP-STM)也觀測到了自發的的原子級的斯格明子晶體;2015年,杜海峰等[11]通過實驗發現,在外加磁場作用下,FeGe納米帶中邊緣扭曲的螺旋基態可以演變成斯格明子,即利用邊界效應實現斯格明子的產生;Hsu等[12]證明了局部電場可以實現斯格明子與鐵磁態之間的相互轉換.此外,許多研究者[13?20]也進一步研究了室溫下斯格明子的形成及其基本操控.其中,Zhou和Ezawa[17]以及Jiang等[18]分別通過模擬和實驗實現了室溫下受限幾何結構中帶狀磁疇向單個斯格明子的轉換.無疑,這些結果都為斯格明子自旋電子設備的應用打開了一扇大門.
斯格明子的自旋結構[21,22]如圖1所示,其中心處的自旋向下,而邊緣處的自旋向上,中心與邊緣成反平行排列,而中間的過渡區域磁矩由向下逐步轉到向上.因此,斯格明子也是一種特殊的磁疇壁結構.此外,類似于磁疇壁,根據磁矩的兩種不同轉動方式,將斯格明子分為布洛赫型和奈爾型兩大類.
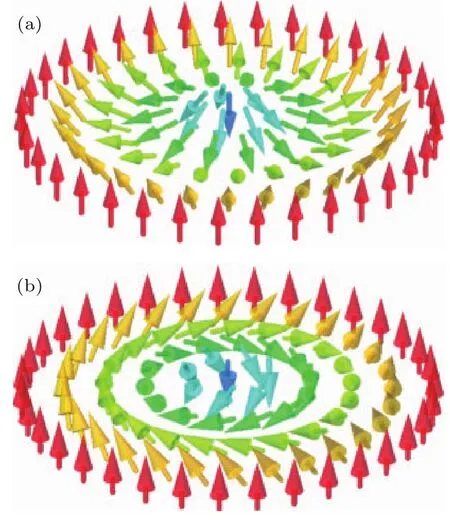
圖1 兩種斯格明子的自旋結構 (a)奈爾型斯格明子;(b)布洛赫型斯格明子[21,22]Fig.1.The magnetic texture of two types skyrmions:(a)Néel-type skyrmions;(b)Bloch-skyrmions[21,22].
磁有序系統中穩定斯格明子的機理有四種,分別是:長程偶極相互作用,Dzyaloshinskii-Moriya相互作用(DMI),阻挫交換相互作用以及四自旋相互作用,并且多種機理可能會同時作用[3].特別地,DMI是目前研究最多的一種.通常在非中心對稱的塊狀磁性材料和界面反演對稱性破缺的過渡金屬薄膜中,由于這些材料中的原子排列結構對稱性極低,并且存在較強的自旋軌道耦合,往往會產生DMI.此外,在Co/Ru/Co多層膜納米盤[23]中,Dai等[24]通過微磁模擬發現,在該體系中雖然不存在DMI,但由于幾何限制以及各種微磁學能量之間的競爭也可以自發地形成穩定的斯格明子基態.近年來,有大量的理論與實驗工作都用于研究單個孤立斯格明子的產生、驅動、刪除、探測等基本操控,并期望將其運用在自旋電子學器件中,如:賽道存儲、邏輯門、振蕩器等.尤其是與傳統的磁疇相比,斯格明子的驅動電流更小,從能源的角度來看,將更適合用于未來的信息存儲設備.
對于信息存儲,最傳統的方式是硬盤存儲和隨機存儲(random access memory,RAM),它們都曾經歷過迅猛的發展.其中,硬盤存儲是將信息(數據)存放在硬盤內的磁盤上,啟動時,硬盤高速旋轉,磁頭將會讀出相應的數據.對于這一設備,雖然價格比較低廉,信息可以長期儲存,但是由于存在大部件的機械運動,可能會造成機械零件以及能量的損耗;其次,外界的振動和干擾對其影響也較大.而隨機存儲器則是利用晶體管和電容器中的電子態來存儲數據位[25],并與CPU直接交換數據,可以隨時讀寫,速度很快,分為靜態隨機存儲器和動態隨機存儲器.不足的是,這種存儲器在斷電以后,內部存儲的信息就會消失,使用壽命短暫,讀寫次數有限.此外,在實現了利用電流誘導磁性隧道結(magnetic tunnel junction,MTJ)中的磁矩翻轉以后,基于MTJ的自旋轉移矩磁性隨機存儲器(spin transfer torque magnetic random access memory,STT-MRAM)立即成為一個研究熱點,得到了大量科研人員的關注,其主要原因在于該存儲設備的非易失性好、存取速度快以及無限持久力[26,27].但在投入實際生產之前,對于該設備的能耗、熱穩定性、信息的可靠性等問題,還有待繼續研究.基于以上分析,這些存儲設備都各有優劣,而對于現在的信息化時代,人們都期望能夠擁有一種同時結合上述存儲器優點的新型設備來儲存信息,即價格便宜、讀寫速度快、信息可靠、能耗低并且非易失性好.幸運的是,在十多年前,Parkin等[25,28,29]提出了一種新的存儲方式——賽道存儲(racetrack memory,RM),在這一模型中,納米線作為賽道,數據全部儲存在賽道上的磁疇壁中,這些疇壁是非易失的,可以實現信息的復寫.有別于傳統的硬盤存儲,它沒有運動的大部件,而是攜帶信息(二進制數據)的磁疇壁在賽道上來回運動,從而實現信息的讀寫存儲.因此,賽道存儲具有較強的防震性與抗干擾性,有利于移動設備的信息存儲.理論上當利用自旋極化電流驅動疇壁時,速度可達到每秒幾百米甚至數千米[30,31],可見這一設備的數據讀寫速度也是很可觀的.
綜合考慮斯格明子的優良特性,并結合基于磁疇的賽道存儲機理,文獻[3,32—36]提出磁性斯格明子也可以作為信息的載體用于賽道存儲,因此引發了大量相關的實驗和理論工作,比如:斯格明子在賽道上的多種產生方式、驅動過程以及讀出過程.Romming等[34]和Sam paio等[37]分別在實驗和理論上利用自旋極化電流實現了斯格明子的產生,這為斯格明子的賽道存儲提供了無比重要的基礎條件.有研究發現[38?40],相比于傳統的磁疇壁,驅動斯格明子的電流密度小了5—6個數量級[32],從而降低了能耗,符合當代“綠色環保,節能減排”的科學發展觀.并且,這種以斯格明子為基礎的賽道存儲能突破磁疇壁賽道存儲的密度極限,極大地提高了存儲密度.因此,集各種優勢于一身的斯格明子賽道存儲將有望成為下一代磁性存儲的主導.
本文詳細介紹了斯格明子在賽道上的寫入、運動和讀出這三個基本過程.在第2部分主要介紹斯格明子在賽道上的多種寫入方式,包括注入自旋極化電流、外加磁場和激光加熱等,同時,考慮到實際應用的需要,也對室溫下斯格明子的產生做了簡要的論述.第3部分討論斯格明子在賽道上的驅動方式,其中,注入自旋極化電流,不論是操作的簡易度還是能量的利用率,都是比較有效、也有望應用于實際的一種方式.第4部分簡要地介紹斯格明子在賽道上的讀出過程,主要論述了拓撲霍爾效應和磁阻效應.特別地,非共線磁阻效應作為一種新的全電氣化方案將有望應用于未來的斯格明子賽道存儲設備中.本文第5部分針對斯格明子在極化電流的驅動下所產生的斯格明子霍爾效應,介紹了幾種消除這一效應的方法.
2 斯格明子在賽道上的寫入
斯格明子是一種拓撲數為1的自旋結構,而自旋螺旋態或者鐵磁態都是拓撲數為0的拓撲平庸態.對于這些拓撲數不同的自旋結構,它們不可能通過連續形變從一種狀態過渡到另一種狀態,即在這些態之間存在著一個有限的能量勢壘,并以此將它們區分開[34,41].因此,如果要實現兩種自旋結構的轉換,必須要克服它們之間的拓撲勢壘[22,37].最常用的方法有:注入自旋極化電流、外加磁場、局部加熱等.然而,在實際應用中,我們都期望能在室溫下進行操作,因此,本部分也對斯格明子在室溫下的產生(即成核)情況做了簡要的論述.
2.1 自旋極化電流誘導斯格明子的產生
對于普通電流,是由自由電子的定向移動而形成,電子所攜帶的自旋方向隨機分布,總體不帶極性.當普通電流穿過“鐵磁層/非鐵磁層/鐵磁層”三明治結構的自旋閥時,由于自旋散射作用,最終將使普通電流變成自旋極化電流.利用自旋極化電流來產生斯格明子,不論是實驗還是理論的角度,無疑都是一種比較簡單、有效、也有望應用于實際的產生方式.
2.1.1 實驗研究
相比于傳統的磁疇壁[42],斯格明子具有特定的手性,要想清楚地知道其內部磁矩的具體分布,在實驗上就需要更為復雜的流程.除了利用小角度中子散射實驗和洛倫茲透射電鏡研究斯格明子,自旋極化掃描隧道顯微術[43?46]作為一種新興的、空間分辨率能達到原子尺寸的表面自旋分辨技術,也可實現對真實空間中斯格明子的研究[34].當其只用于研究表面磁結構及其特性時,為了不改變或者破壞樣品的本身結構、影響SP-STM成像,一般利用低電壓(約為幾十毫伏)和低電流(約為幾十納安)來掃描樣品表面.若加大掃描電壓和隧穿電流,則通過針尖的特殊結構將產生高能的自旋電子,形成自旋極化電流注入到材料的表面,實現對樣品的操控.
Romm ing等[34]就利用SP-STM對PtFe表面進行處理,通過注入自旋極化電流來控制斯格明子的成核與湮沒.考慮到鐵磁態(Q=0)與斯格明子態(Q=1)之間相互轉換時會出現明顯的磁信號,因此,可以作為這兩者之間的轉換信號.為了進一步研究在自旋極化電流下鐵磁態與斯格明子之間的轉換機理,Romm ing等主要探究了轉換率f和出現斯格明子的概率P分別與掃描電壓U,隧穿電流I,以及外磁場B之間的關系[47,48].實驗結果顯示,自旋極化電流所引起的熱燥聲和焦耳熱的影響可以忽略不計,而注入電子的能量eU是影響轉換率的主要因素,如圖2(a),電壓越大,轉換率f越大.除此之外,通過圖2(b)的P-B關系可以清楚地看到,當固定入射電子的能量|eU|和隧穿電流I的大小時,對于大小相同、方向相反的兩個掃描電壓,即電流的方向相反,整個圖線會出現一個?B≈100 mT的平移,而且自旋極化電流所產生的自旋轉移力矩(spin-transfer torque,STT)主要與電流的極化強度和方向有關.由此表明,引起兩條圖線發生?B的平移,其主要原因就是兩者的自旋轉移力矩的不同.因此,STT將是一種新的控制自旋結構轉換方向的方法,同時也是一種很有效的操控單個斯格明子的方式.

圖2 T=4.2 K時電壓和外場對斯格明子成核和湮沒的影響[34] (a)轉換率f與電壓U的關系(I=300 nA,B=2.7 T);(b)斯格明子概率P與外場B的關系(I=100 n A)Fig.2. Voltage and magnetic field characteristics of skyrmion creation and annihilation at T =4.2 K[34]:(a)Measured switching rates f depend sensitively on U(I=300 n A,B=2.7 T);(b)the relationship between skyrmion probability P and field B(I=100 nA).
2.1.2 數值模擬
目前,在實驗上已經觀察到了單個的斯格明子或者斯格明子晶體,而且通過SP-STM向薄膜材料注入自旋極化電流,在外場的作用下也可實現斯格明子的成核和刪除[34].但是對于實際應用,不僅是斯格明子的賽道存儲,基于斯格明子的其他自旋電子設備也一樣,它們都需要一種更簡單有效的方法來產生或者操控斯格明子,這也正是當前在實驗上所面臨的挑戰.而通常情況下,一定的數值模擬工作可以為實驗研究做出重要的指導,因此,對于利用自旋極化電流產生斯格明子,數值模擬也是必不可少的.目前,在這一領域已有不少的理論工作.
其中,Sam paio等[37]在這一領域做出了具有里程碑意義的重要工作,他們通過微磁模擬軟件The Object Oriented Micro Magnetic Framework(OOMMF)進行模擬,研究了不同參數對單個斯格明子的大小及穩定性的影響.Rohart和Thiaville[49]的計算結果表明,對于較小的D值,斯格明子的大小對納米盤的依賴性較小,而對于較大的D值,由于納米盤的邊界影響,斯格明子的大小會隨著盤的增大而增大(如圖3所示).文獻[22]中還提到只有當電流超過一個閾值,并且經歷一定的弛豫時間,斯格明子才能產生.對實際應用而言,臨界電流和弛豫時間無疑都是至關重要的因素,臨界電流越小,耗能越低,弛豫時間越短,則有效性和靈敏度越高.有研究發現臨界電流的大小與材料的阻尼系數α有關,α越小,成核所需的臨界電流就越小[37].對于CoFeB薄膜,其阻尼系數α=0.015,此時,臨界電流可以減小到0.5×108A·cm?2.其次,減小磁晶各向異性常數或增加外磁場,也可以減小臨界電流[37].此外,Iwasaki等[33]在帶有缺口的垂直磁化的納米線上注入脈沖電流,通過自旋轉移力矩的作用可以產生布洛赫型的斯格明子.Yuan和Wang[50]研究了在自由層是垂直磁化的自旋閥中通入納秒級電流脈沖,即使沒有外場的幫助,也可以實現斯格明子的成核和刪除.

圖3 在不同大小的圓盤中斯格明子的半徑隨D/D c的變化[49]Fig.3.Variation of the skyrmion core radius R s versus D for different dot radius.The radius is defined at the m z=0 line[49].
對圓盤產生斯格明子的研究為斯格明子賽道存儲打下了堅實的基礎.在納米賽道中,產生單個斯格明子或者斯格明子鏈的方法有很多,目前比較常用的就是注入自旋極化電流.對斯格明子而言,存儲器中的納米賽道是一個受限系統.因此,斯格明子的產生、運動以及湮沒過程都會受到鐵磁納米賽道邊界的影響[33,36,51?53].最近有關研究表明,在具有DMI的納米薄膜上,邊界的不穩定性可能會導致斯格明子在其邊界附近產生[54].另外,斯格明子在受限系統中的運動也會受到邊界的作用,包括振蕩和回旋運動[55?57],而且賽道的寬度會直接影響斯格明子的大小和斯格明子間的平衡距離[36].Ran等[58]基于微磁學模擬,系統地研究了在受限系統中斯格明子成核的邊界效應.圖4為自旋結構在不同的注入電流j下隨d1的變化,其中d1是賽道左端到注入中心的距離.除了距離d1,材料參數、賽道幾何參數和電流密度也會對受限系統中斯格明子的成核情況產生影響.文獻[58]中指出斯格明子態只能在特定的參數區間產生.

圖4 自旋結構在不同電流密度j下隨d1的變化 形成事件的成功或失敗表示的是斯格明子形成的成功與否,黃色箭頭指出的是自旋結構中的類缺口點,比色刻度尺表示的是磁矩z的分量[58]Fig.4.Spin structures varying with the distance between the current injection point and the left end d1.The success or failure of the generation event rep resents whether a sTable skyrmion is generated successfully or not.The yellow arrow indicates the defect-like point in the spin structure.The color scale shows the z-component of the magnetization[58].
2.2 外加磁場下斯格明子的產生
2.2.1 斯格明子的B-T相圖
在一個自旋體系中,由于磁交換、自旋軌道耦合以及靜磁效應的存在,通常會使自旋之間產生多種不同的相互作用,如交換相互作用、磁晶各向異性相互作用、退磁相互作用等.特別地,在非中心對稱的塊狀磁性材料和反演對稱性破缺的過渡金屬薄膜中,由于這些材料的對稱性極低,并且存在較強的自旋軌道耦合,從而會產生一個較強的DMI[59,60].對于整個體系,它的哈密頓量可以寫成如下形式[61]:
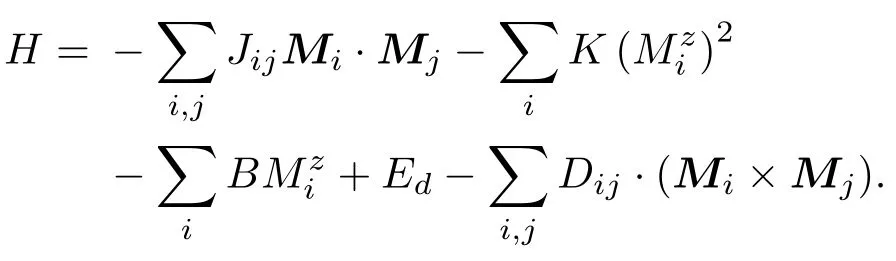
等式右邊各項分別代表交換能、磁晶各向異性能、塞曼能、退磁能和DMI能.其中磁交換相互作用是使相鄰磁矩平行或反平行排列,而DMI則更傾向于使相鄰磁矩垂直排列[41].因此,在這一體系中,各種相互作用進行競爭,最終可形成多種亞穩態(即能量極小).Mühlbauer等[8]首次在MnSi手性磁體中利用小角度中子散射實驗證明了斯格明子晶體的存在,并被確認為A相[62](如圖5).從相圖中可以看到,A相處在居里溫度附近,當外場比較小時,螺旋態最為穩定,加大磁場,螺旋態過渡到圓錐態,若繼續加大磁場,最后形成與外場同向的鐵磁態.從橫向來看,增加體系的溫度,由于熱擾動的作用,使圓錐態轉化為穩定的斯格明子態(即A相),但斯格明子晶體只能在較小的一個溫度范圍內.研究發現,材料的厚度會影響斯格明子的熱穩定性,材料越薄,存在斯格明子相的溫度范圍越大,Yu等[63]對FeGe的觀測也進一步說明了斯格明子的穩定性對材料厚度的依賴性.事實上,在二維的螺旋磁體中,斯格明子晶體能夠在較大的溫度和磁場范圍內穩定存在[64,65].
改變體系的磁場強度來產生斯格明子是一種最基本的方式.理論上已經討論了在磁場作用下,單軸各向異性、不均勻手性調制等對斯格明子穩定性的影響[66?71].此外,Romm ing等[34,72]也進一步研究了單個斯格明子的大小和形狀對外場的依賴性.

圖5 MnSi關于磁場和溫度函數的相圖[3,8]Fig.5.The phase diagram of MnSi as a function of T and B[3,8].
2.2.2 外加磁場誘導室溫斯格明子的成核
對于生長在重金屬上的磁性薄膜,如生長在Ir上的Fe單層膜或者Pd Fe雙層膜,亦或是直接生長在Cu基片上的FeNi雙層膜等,在這些體系中如果要形成穩定的斯格明子,通常需要較大的磁場(約1 T)和極低的溫度(約幾十K).無論是從能量的有效利用還是實驗的操作難易度來講,這都不是我們最想要的結果.對于實際應用,我們都期望能在室溫下操控穩定的斯格明子,而要實現室溫下的操控,其前提是能在室溫下產生穩定的斯格明子.最近,Moreau-Luchaire等[20]利用非對稱多層膜體系,實現了室溫下單個斯格明子的成核,并且所需要的外場很小(約幾十毫特斯拉),從而大大地降低了能耗.
這種非對稱多層膜的物理結構為:在不同的重金屬薄膜層(如Ir和Pt)之間夾一鐵磁層,形成“重金屬A/鐵磁層/重金屬B”的三明治結構,并以此為基本單元,重復疊加,形成多層膜.這一新型的體系主要有兩大優勢,首先,由于磁性薄膜的多次疊加,有效的磁體積增大,可以大大提高體系的熱穩定性.其次,如果重金屬A和B與鐵磁層的界面DMI剛好相反,則在“重金屬A/鐵磁層/重金屬B”三層膜中,鐵磁層能得到一個較大的附加手性相互作用.
如圖6(a),該多層膜的基本單元為Ir/Co/Pt,Co/Ir之間的DMI與Co/Pt之間的DMI方向相反[73],因此,鈷層上下表面的DMI方向一致,使鈷層附加一個很大的DMI.通過掃描透射X射線顯微術(STXM)成像,可以很清楚地觀測到該體系的磁結構隨外場的變化,如圖6(b).在完全磁化之前,當外場μ0H⊥=68 mT時,出現了圓形磁疇,選取特定的圓形磁疇,研究其大小與外場之間的變化關系,得到如圖6(c)的X射線磁圓振二向色性信號(XMCD)圖,將實驗所得的數據與數值模擬[74]的結果進行對比,最后證實了鈷層確實有很大的DMI(D約為1.9 mJ·m?2),而且圓形磁疇也正是由較大的界面DMI所產生的拓撲數為1的斯格明子,而不是由偶極相互作用產生的磁泡[75?77].此外,還通過實驗研究了由該多層膜構成的納米盤和納米軌道上斯格明子大小隨外場的演變過程,并與微磁模擬進行對比,兩者能夠很好地符合.綜上所述,考慮到這種非對稱多層膜的兩大優勢,不僅能實現在室溫下單個斯格明子的成核,而且僅需要幾十毫特斯拉的外場就能穩定小于100 nm的斯格明子.顯然,這一突破性進展又為斯格明子賽道存儲的設計提供了新的思路.
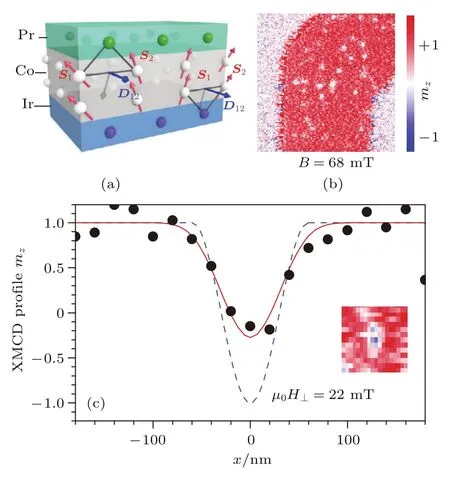
圖6 非對稱多層膜中斯格明子的成核 (a)多層膜的基本單元Ir/Co/Pt,及鈷層與Pt和Ir層之間的附加DMI的示意圖;(b)外場B=68 mT時,STXM成像;(c)外場B=22 mT時,圓形磁疇(斯格明子)的XMCD圖,其中虛線為理想的半徑為60 nm斯格明子的磁化曲線[20]Fig.6. The creation of skyrmion in asymmetric magnetic multilayers:(a)Illustration of the additive Dzyaloshinski-Moriya interaction(DMI)induced by different heavy metals(Ir and Pt)sandwiching a magnetic layer(Co);(b)a 1.5×1.5μm2 out-of-plane magnetization(m z)map obtained by STXM on a(Ir|Co|Pt)10 multilayer at r.t.for applied out-of-plane magnetic fields of 68 mT;(c)experimental X-ray magnetic circular dicroism(XMCD)signal through a magnetic circular domain(skyrmion)as observed at 22 mT(b lack dots),and the blue dashed curve is the magnetization profile of an ideal 60 nm-diameter skyrmion[20].
2.3 其他成核方式
除了上面所介紹的方法,Zhou和Ezawa[17]以及Jiang等[18]分別從理論和實驗提出了另一種成核方式,即在一個對稱的受限幾何結構中,帶狀磁疇通過連接左右對稱區域的窄條,可以轉換成斯格明子.如圖7,該體系所選用的材料為Ta/CoFeB/TaOx,初始時,窄條的左右兩邊都是飽和的磁化狀態,加上垂直外場B=+0.5 mT時均產生不規則的帶狀磁疇,從左端通入時間為1 ns,大小為5×105A·cm?2的單脈電流后,磁疇開始運動,到達細頸時,由于幾何限制,電流不均勻分布,從而驅動磁疇通過細頸.有趣的是,當磁疇到達細頸末端時,就會轉變成完整的斯格明子泡泡到達右邊區域,由于受拓撲保護作用,右邊的斯格明子就會一直穩定地存在,可進行有效的電流驅動.這個動態過程類似于用吸管吹肥皂泡的過程,因此,也把這種成核方式形象的稱為“吹斯格明子”.雖然通過這種動態的成核方式所產生的斯格明子尺寸偏大(一般為幾百納米,甚至是1μm),但是可以適當地調節材料的具體參數,改變各種相互作用的競爭,使斯格明子的尺寸減小[37,49,78],而且這種方法已經實現了在室溫下的操控,所以有望應用于斯格明子的賽道存儲.

圖7 斯格明子泡泡在Ta/CoFeB/TaO x三層膜的受限幾何結構中由電流誘導的成核過程[18]Fig.7.The nucleation of skyrmionic bubbles in a Ta/CoFeB/TaO x trilayer by the current-induced expansion of domains at the exit of a constriction[18].
此外,Koshibae和Nagaosa[79]從理論上提出可以用激光輻射進行局部加熱來產生斯格明子.這種方法的物理模型與自旋極化電流產生斯格明子非常相似,所不同的是這里取一個圓形區域進行局部加熱,而不是注入自旋極化電流.利用這種方式也可以產生單個斯格明子,且主要取決于加熱的強度和時間.但是,由于需要提供激光裝置,若用于賽道存儲的寫入磁頭,可能會使裝置變得更為復雜.
3 斯格明子在賽道上的運動
在討論了斯格明子的成核問題之后,我們所關心的另一個問題就是如何去驅動它.在此之前,人們對于疇壁的研究相對而言較為成熟,其中,利用電流驅動疇壁的研究激發了人們將類似的方法應用于斯格明子驅動上的靈感,并且最初發現斯格明子晶體的材料都具有一定的導電性.因此,在有關斯格明子賽道存儲器的研究中,注入電流也就成為了較早的一種驅動方法.當注入自旋極化電流時,傳導電子的自旋和斯格明子中的磁矩發生相互作用,產生自旋轉移力矩,從而促使斯格明子運動.當然,隨著科技的進步,越來越多的驅動方法不斷涌現出來,其中的機理也不盡相同.因此,本部分我們主要對驅動斯格明子的一些基本方法做簡要的論述.
3.1 自旋極化電流驅動斯格明子
近年來,利用自旋極化電流驅動斯格明子,不僅在理論計算和數值模擬上取得了重大突破,在實驗上也有很大的進展.2010年,Jonietz等[80]在MnSi中首次發現了電流可以誘導斯格明子晶體的運動;2012年,Yu等[81]利用洛倫茲透射電子顯微鏡在FeGe中直接觀察到了電流誘導Bloch斯格明子晶體的運動;Woo,Tokunaga等多位研究者[13?18]也進一步研究了室溫下斯格明子在電流驅動下的運動情況.此外,Schulz等[38]和Everschor等[40]分別利用貝里相分析和Thiele方程理論解析得到了斯格明子的運動,這些工作都證明了斯格明子確實能像磁疇壁一樣,可以通過自旋極化電流所產生的自旋轉移矩來進行驅動[33,37,39].
3.1.1 自旋極化電流的兩種注入方式
利用自旋電流驅動斯格明子時有兩種注入方式,即面內注入(current flowing in the film plane,CIP)和垂直膜面注入(current flowing perpendicular to the film plane,CPP)[82?84].前者是平行于鐵磁層面內注入自旋極化電流,對局域磁矩產生面內自旋轉移力矩從而驅動磁性斯格明子;后者則是垂直于鐵磁層注入自旋極化電流,為實現這一操作,通常可以利用自旋閥或者磁性隧道結,亦或是自旋霍爾器件來產生自旋極化電流.對于自旋閥或者磁性隧道結[85,86],普通電流經過釘扎層后變成極化電流,通過間隔層后便作用于鐵磁自由層;而對于自旋霍爾體系[87?90],由鐵磁層和重金屬層構成雙層膜結構,向重金屬層注入普通電流后,由于重金屬層的自旋散射作用,使重金屬層上下表面積累反向的自旋電子,從而形成純自旋流垂直注入鐵磁層.自旋極化電流或者純自旋流通過鐵磁層時都會對局域磁矩產生自旋轉移力矩的作用,從而使斯格明子發生運動.
在微磁學模型中,三維含時的磁化動力學方程為Landau-Lifshitz-Gilbert(LLG)方程,考慮自旋極化電流的作用時,其形式為

其中Ms為飽和磁化強度,m=M(r,t)/Ms=m(r,t)為單位磁化矢量,表示任一時刻和位置的磁矩方向;γ為旋磁比;Heff為與交換能、磁晶各向異性能、塞曼能及DMI能等有關的有效場;α為阻尼系數.方程右邊第一項表征磁矩繞著有效場的拉莫爾進動,第二項表示磁矩向平衡態弛豫的阻尼力矩,第三項即為自旋極化電流所產生的自旋轉移力矩.
對于面內注入[37,83,91],

對于垂直膜面注入[84,94,95],

其中b=γ~p/(2μ0eMstF),tF為鐵磁層厚度,p為自旋極化率,為極化單位矢量;若為自旋霍爾器件,則j=jHM,p=?SH,jHM,?SH分別表示通過重金屬層的普通電流大小以及自旋霍爾角.對于自旋霍爾器件,除了上面所提到的力矩,實際上,由于界面效應(如Rashba edelstein效應[96]),還存在一個正交的類場力矩,但這一力矩的影響較小,斯格明子的運動通常主要取決于上面所提及的力矩,因此,在進行解析計算或數值模擬的時候,往往忽略掉了類場力矩.
3.1.2 斯格明子的運動特點
在利用自旋極化電流(或純自旋流)驅動斯格明子時,無論是面內注入還是垂直注入,斯格明子往往同時具有縱向(沿電流方向)和橫向(垂直于電流方向)兩個方向的運動.Iwasaki等[39]首次利用數值實驗展示了在無限大MnSi膜中面內注入電流驅動Bloch斯格明子晶體的情形,結果顯示,斯格明子的去釘扎電流明顯比螺旋相的小,并且當α=β時,斯格明子呈現出縱向和橫向兩個方向的速度,橫向速度主要是由于斯格明子的非拓撲平庸結構,使得拓撲數不為0,從而引起一個不為0的馬格努斯力的作用,導致斯格明子發生橫向漂移,通常稱之為斯格明子的霍爾效應.Sampaio等[37]利用微磁模擬,研究了面內注入電流時Néel斯格明子的運動情況,與Bloch型斯格明子一樣,當α=β時,有兩個速度分量,而當α=β時,只有縱向速度,這與Thiele方程[97]解析推導得到的結果一致,
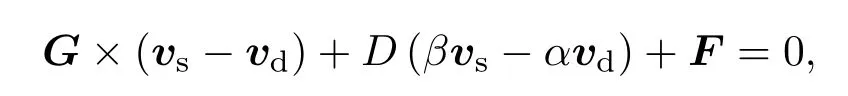
從圖8中可以清楚地看到速度的大小與驅動電流的大小成正相關,驅動電流越大,斯格明子的速度越大,對于斯格明子的賽道存儲,為了提高信息的存取效率,我們肯定期望速度越大越好,即增加驅動電流.但是,在電流增加的同時,斯格明子的橫向速度也在增加,當電流超過某一臨界值時,斯格明子受到的馬格努斯力將大于賽道邊界的排斥作用,從而導致斯格明子的湮沒,攜帶的信息也隨之丟失,這不是我們希望看到的結果,所以,驅動電流也不是越大越好,要綜合考慮邊界的排斥作用力.但是,若想得到更大的速度,就必須設法增加邊界勢壘,或者利用其他的方法來抑制斯格明子的霍爾效應,相關的內容將在本文的第5部分會有較詳細的介紹.
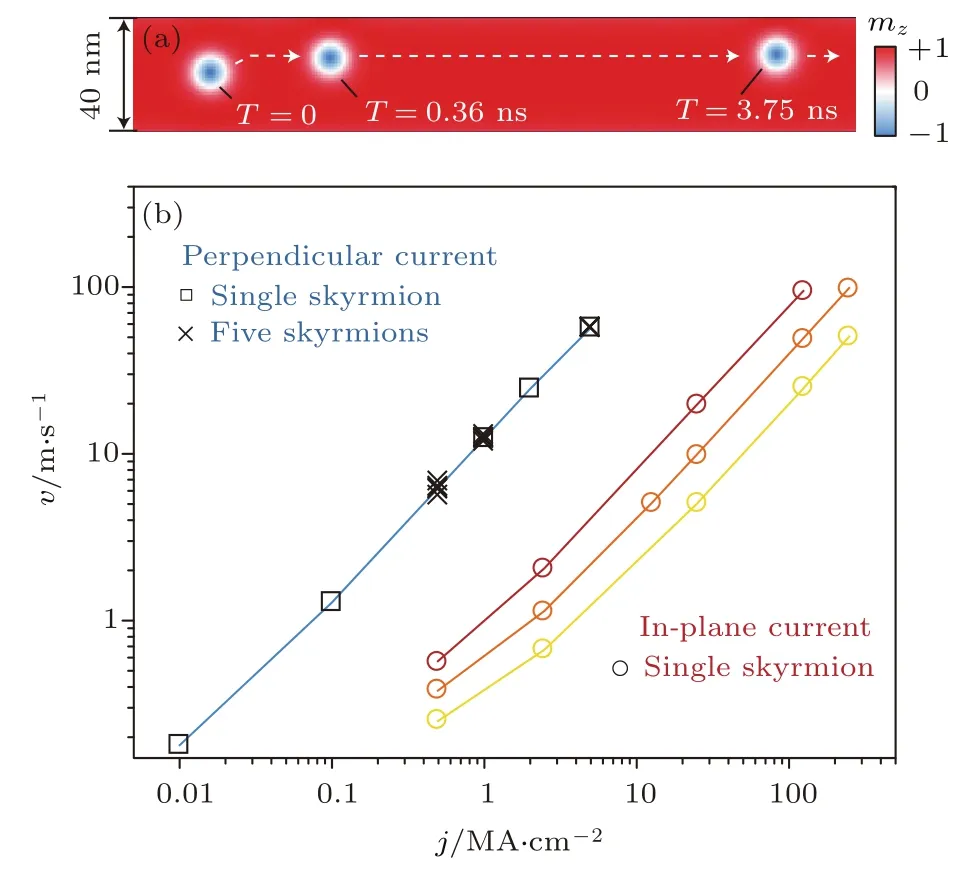
圖8 (a)垂直注入自旋極化電流后斯格明子在納米賽道上的運動軌跡;(b)在垂直膜面注入(藍色線)和平行面內注入(黃色、橙色、棕色分別代表β為0.15,0.30,0.60)的兩種方式下斯格明子的縱向速度v與電流密度大小j的關系[37]Fig.8.(a)Trajectory of a skyrmion driven by a vertical spin-polarized current in a nanotrack;(b)skyrmion velocity v as a function of current density j for in-plane currents with different values of the non-ad iabaticity parameter β(0.15,0.30 and 0.60 in yellow,orange and brown lines and circles,respectively)and for vertical currents(blue line,squares for isolated skyrmion,crosses for the chain)[37].
3.1.3 斯格明子間及其與邊界的相互作用
在基于斯格明子的賽道存儲中,斯格明子作為數據位來存儲信息.因此,斯格明子比特之間的間距能在很大程度上影響存儲器的存儲密度,其間距越小,存儲密度越大.當然,我們想要的存儲密度是越大越好,也就是斯格明子比特間距越小的情況.但是由于兩個斯格明子的自旋構形有重疊部分,導致了斯格明子間的相互作用,并隨著間距的增大而呈指數減小[98].當斯格明子的初始間距di較小時,間距會隨著斯格明子的運動而變化.有關CoPt材料[32,36,37]的模擬結果顯示:當di=30 nm時,斯格明子間距在0—1 ns時顯著增加;當di增加到57 nm時,間距的增加速度大幅度減小;繼續增大di到62 nm,在模擬的時間內間距基本不變.所以,對于這些材料來說,di>62 nm可以作為寫入和讀取連續斯格明子比特過程的理想間距,也叫比特長度.從模擬結果中可以看出,di>57 nm也是一個可行的斯格明子比特間距.并且在Fert等[32]和Sampaio等[37]的研究中所采用的斯格明子比特間距為60 nm,恰好也證實了這個結論.對于更普遍的情況,理想間距約為材料的DMI螺旋長度LD(LD=4πA/|D|)[99],可行的間距約為0.9LD.

圖9 在寬為40 nm的跑道上,垂直注入驅動電流,斯格明子比特鏈在不同的賽道末端和不同時刻的運動情況 賽道末端沒有三角形凹槽,(a)t=0 ns,(b)t=10 ns;賽道末端有三角形凹槽,(c)t=0 ns,(d)t=0.95 ns,(e)t=0.975 ns,(f)t=1 ns,(g)t=1.025 ns,(h)t=1.05 ns,(i)t=1.075 ns,(j)t=1.1 ns,(k)t=1.125 ns,(l)t=1.15 ns[36]Fig.9.Vertical-current-d riven motion of a skyrmionic bit chain at the end of the 40-nm-wide racetrack without any notch at(a)t=0 ns,(b)t=10 ns,and at the end of the racetrack with a notch at(c)t=0 ns,(d)t=0.95 ns,(e)t=0.975 ns,(f)t=1 ns,(g)t=1.025 ns,(h)t=1.05 ns,(i)t=1.075 ns,(j)t=1.1 ns,(k)t=1.125 ns and(l)t=1.15 ns[36].
當斯格明子運動到讀出元件時,讀出元件將斯格明子攜帶的信息由磁信號轉化為其他形式的信號.此后,斯格明子不能再次進入使用.當其靠近賽道末端時,由于斯格明子之間和斯格明子與邊界[33,36]的排斥作用,斯格明子會在賽道的末端發生擁堵,其間距和大小都明顯變小,如圖9(a)和圖9(b)所示.雖然電流能使斯格明子順利地離開賽道,但需要足夠大的電流密度(在參考文獻[36]中約為1011A/m2),才能使斯格明子在電流的驅動下克服賽道末端邊緣的排斥力而離開賽道,從而導致高能耗.Zhang等[36]提出在賽道末端設計一個三角形凹槽來避免斯格明子的堵塞,如圖9(c)—(l).這種方案可以利用高分辨率的納米光刻來實現,而且不需要增大電流.圖9(d)—(l)顯示了斯格明子在0.2 ns內的抹除過程.當移動的斯格明子靠近凹槽邊緣時,斯格明子轉化為疇壁,然后通過電流最終被清除.在這一過程中,斯格明子比特鏈在末端并沒有發生擠壓,而是連貫地一起運動,表明這種方案在技術層面,傳輸和擦除數據具有一定的可行性.
3.2 壓控磁各向異性效應
在操縱斯格明子運動方面,最近比較熱門的是利用壓控磁各向異性 (voltage-controlled magnetic anisotropy,VCMA)效應來控制斯格明子的運動.通過外加局域電場導致電荷積累,因此,外加電場區域的垂直磁各向異性(perpendicular magnetic anisotropy,PMA)發生改變,影響斯格明子的運動[100,101]. 其中,外加電場區域的PMA值Kuv與電場強度E呈線性變化關系,Kuv=Ku+?KuvE[100,102],?Kuv是一個由電壓導致垂直各向異性變化的強度來決定的物理量.Shiota等[103]的實驗已經證實這一線性關系.本節主要介紹近年來關于壓控磁各向異性效應下斯格明子運動的研究.
3.2.1 基于斯格明子的類晶體管器件
Zhang等[104]基于壓控磁各向異性效應設計了一種斯格明子類晶體管器件,門控電壓施加在納米賽道的中心區,在距離納米賽道左端90 nm處利用磁隧道結產生一個斯格明子,然后通過自旋電流使它向賽道右端移動.門控區域的PMA值可以通過局域的外加電壓來控制,也就是上面所說的壓控磁各向異性效應.圖10是驅動電流密度j為5 MA/cm2時不同Kuv下斯格明子晶體管的工作狀態.最初,賽道上沒有注入自旋電流和外加局域電場,斯格明子位于賽道左端,Kuv=Ku,如圖10最上面的賽道所示.在這種情況下,若注入自旋電流,斯格明子能在11 ns后從左邊運動到賽道的右邊,意味著這種條件下電壓門控處于打開狀態(ON).當自旋電流和局域電場打開,對于Kuv=1.10Ku,斯格明子不能進入門控區域,將被釘扎在電壓門控的左端,此時的電壓門控處于關閉狀態(OFF).對于Kuv=0.90Ku,斯格明子能進入門控區域但不能從電壓門控的右端離開,并在靠近右端時發生釘扎,表明電壓門控是關閉狀態.
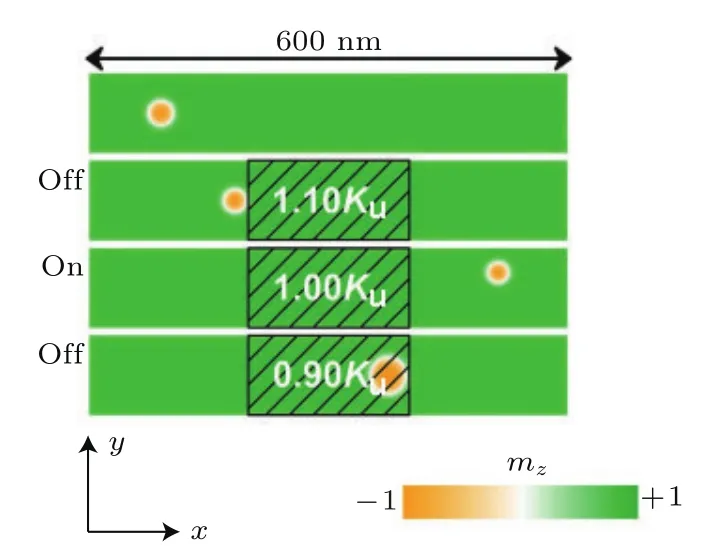
圖10 在相同的時間和工作條件下,納米賽道的俯視圖,彩色部分表示磁化強度的面外分量,黑線陰影表示電壓控制的PMA區域[104]Fig.10.The top-view of the nanotracks under the same working conditions at selected times.The color scale denotes the out-of-plane component of the magnetization. The black-line shadows rep resent the voltage-controlled PMA region[104].
當然,斯格明子類晶體管器件的工作狀態不僅可以通過外加局域電場的強度來調節,也受驅動電流的密度j,DMI常數D的影響[104].即使Kuv=Ku,當j大于某臨界值時,其工作狀態也能轉化為打開狀態.而且,斯格明子類晶體管器件工作狀態對DMI常數D也具有依賴性.除此之外,Zhang等還設計了三種不同規格的一類晶體管器件用來研究斯格明子晶體管大小的影響,模擬結果顯示在相同的條件下類晶體管器件的工作狀態是類似的,其結果很好地說明了這種基于斯格明子的類晶體管模型具有穩定性和可縮性.
在納米賽道上,局域的外加電場導致不同的PMA,不同的PMA又會產生勢壘.而斯格明子的能量和大小也受磁各向異性的影響,例如斯格明子能量[104].模擬結果顯示,在納米賽道上可能使斯格明子發生釘扎.若Kuv=Ku,在納米賽道上沒有勢壘,斯格明子在自旋電流的驅動下能順利地從賽道左邊運動到右邊.若Kuv
3.2.2 斯格明子賽道存儲器中電壓門控的應用
壓控磁各向異性效應不僅可以運用在斯格明子晶體管上,還可以運用在斯格明子賽道存儲器中.最近,Kang等[105]基于電壓門控所設計了一種斯格明子賽道存儲器模型.這一模型包含五個部分:產生斯格明子的寫入磁頭,斯格明子運動的納米賽道,讀取斯格明子的讀出磁頭,VCMA門和外圍的互補金屬氧化物半導體電路.剛開始,通過寫入磁頭的自旋閥注入自旋極化電流產生斯格明子.然后,垂直注入的自旋電流驅動斯格明子沿著納米賽道運動,在運動過程中通過改變加在VCMA門上的電壓來調節賽道的磁各向異性,控制斯格明子的釘扎與退釘扎.最后,由于隧道磁阻效應,讀出磁頭的磁隧道節讀取斯格明子所攜帶的信息.
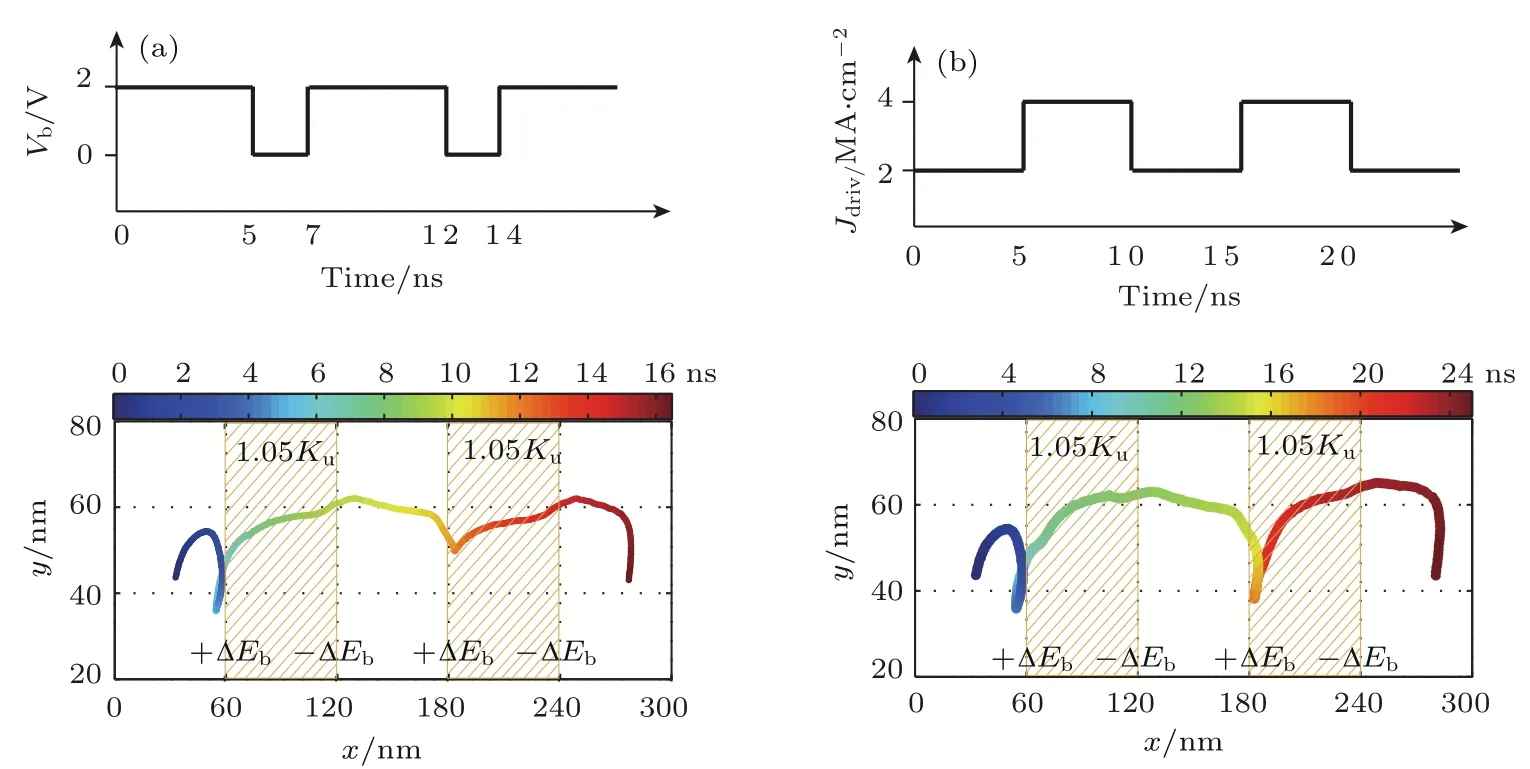
圖11 斯格明子沿納米賽道的運動軌跡 (a)控制電壓的情況;(b)調制驅動電流的情況[105]Fig.11.Trajectory of the skyrmion motion along the nanotrack:(a)The case of controlling the on/offvoltage of the VCM A gate,and(b)the case of modulating the driving current configuration[105].
圖11 所示為上述賽道存儲器模型中控制斯格明子運動的兩種方案.對于第一種方案,斯格明子的運動狀態是通過VCMA門閥區域的電壓精準控制.當外加在門閥區域的電壓斷開,斯格明子所受的驅動力不足以克服VCMA門閥區域的能量勢壘,因此,斯格明子停在門閥區域的左邊.當電壓閉合時,斯格明子通過VCMA門閥,繼續沿著納米賽道移動.斯格明子在此方案下沿著納米賽道的運動軌跡見圖11(a).這種方案可以通過沿著納米賽道均勻地放置VCMA門來實現斯格明子按照時間頻率一步一步地運動.對于第二種方案(如圖11(b)),斯格明子的運動狀態是在VCMA門閥區域的Kuv不變的情況下利用驅動電流來控制.總的驅動電流分為直流和交流部分,直流部分的電流密度是有限的.在直流電流下,斯格明子被釘扎在VCMA門閥區域的左邊,不能順利地運動到納米賽道的右端.然而,當交流電流打開時,斯格明子在總電流的驅動下通過VCMA門閥.這種方案為設計動態調控驅動電流的斯格明子存儲器提供了更多的自由.
3.3 其他驅動方式
最近,Zhang等[106]提出一種新的驅動方式,即利用自旋波驅動納米賽道上的斯格明子.如圖12所示,首先在靠近脈沖元件的右端處產生一個斯格明子并弛豫至穩態或者亞穩態,再將磁脈沖加在脈沖元件上,這時的脈沖元件可以看作是一個微波天線[107?109],最后由此激發的自旋波能驅使斯格明子向賽道的末端移動.除此之外,由于斯格明子的運動會直接影響賽道存儲器的運行,而斯格明子的運動速度vsk就是其中一個非常重要的物理量.通過模擬計算發現:一開始斯格明子是靜止的,當自旋波傳播到斯格明子所在位置時,它開始加速,加速度a與自旋波的量級和斯格明子的半徑rs有關.當DMI常數D增大和PMA常數K減小時,rs增加[36,37],a也跟著增大.當自旋波的振幅和頻率增大,導致較高的能量,因此a也相應地增大.在一段時間后,斯格明子的速度與自旋波的速度vsw相等,vsk(t)=vsw(t).最后,由于自旋波的衰減,vsw(x)=ce?dx,所以斯格明子的速度以指數方式衰減,vsk(t)正比于e?bt,vsk(t)=ate?bt. 另外,交換強度A和飽和磁化強度Ms也會對斯格明子速度產生一定的影響.
此外,斯格明子作為一種準粒子在溫度梯度下的運動并不像疇壁那樣,而是向高溫區域移動,似乎具有負擴散系數,這與通常的布朗運動相反.Zang和Kong[110]對溫度梯度下薄膜中的斯格明子動力學進行了深入的研究,并采用了一種基于磁振子的動力學理論對這一現象給出了解釋.此外,通過磁輔助理論進行數值模擬發現:在外加溫度梯度的條件下,通過調節外磁場H到某一臨界值,斯格明子晶體在擴散過程中一點點地消失,最終在薄膜上產生單個斯格明子.隨著模擬的進行,斯格明子在隨機場的作用下發生運動.斯格明子的運動速度隨溫度梯度的變化如圖13(a)所示,縱向速度vx與溫度梯度呈正比關系,橫向速度vy與溫度梯度的關系也是非零線性的,但是vx比vy要大幾乎一個數量級.除此之外,Gilbert阻尼系數α對斯格明子的運動速度也會產生影響,如圖13(b)所示.縱向速度vx與α呈反比關系,橫向速度vy與α基本無關.
除了以上所提及的方式之外,微波場也可以驅動斯格明子,但是這種驅動方式需要一個前提條件——斯格明子的軸對稱必須被破壞.最近,Wang等[111]利用一個二維系統面內的靜態外場來破壞斯格明子的軸對稱,并通過數值求解二維系統中經典自旋模型的LLG方程,從理論上證明了斯格明子隨微波場的移動.
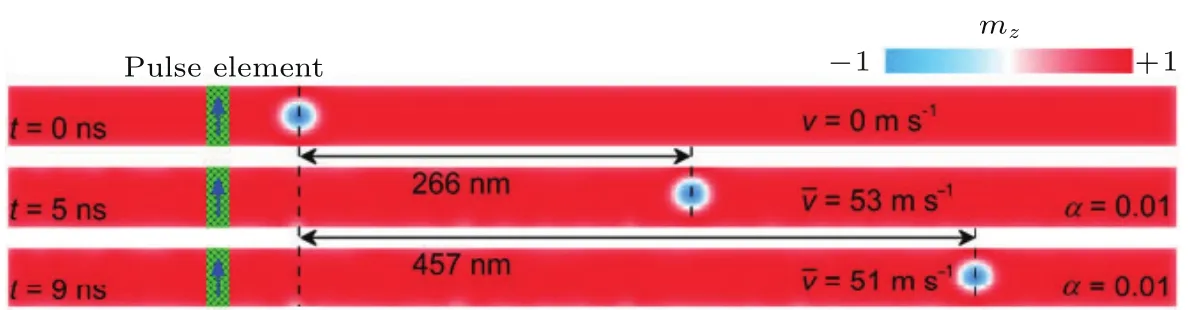
圖12 在納米賽道中,利用SW驅動的斯格明子,有圖案的長方形表示脈沖元素,彩色部分表示磁化強度m z的面外分量[106]Fig.12.The propagation of a skyrmion driven by SW in nanotrack.The pattern boxes denote the pulse elements.The color scale presents the out-of-plane component of the magnetization m z[106].

圖13 (a)斯格明子速度與溫度梯度之間的線性關系;(b)斯格明子速度與Gilbert阻尼系數α的關系[110]Fig.13.(a)A linear scaling between the velocity and the temperature gradient;(b)the scaling of skyrmion velocity with the Gilbert dam ping α[110].
4 斯格明子在賽道上的讀出
在信息存儲的過程中,信息不僅要能完成寫入和傳輸,還要能準確地讀出.而在基于斯格明子的賽道存儲過程中,信息的讀出過程就是探測斯格明子的過程.因此,準確地探測到斯格明子是實現斯格明子賽道存儲的基本條件之一.目前,我們所了解到的主要是考慮利用拓撲霍爾效應和磁阻效應這兩種探測斯格明子的方案來解決讀出問題.
4.1 拓撲霍爾效應
斯格明子是一種特殊的磁疇結構,其中心磁矩與邊緣磁矩呈反平行排列,而中間過渡區域的磁矩連續地轉動.總體而言,斯格明子是一種非共面的自旋結構.當傳導電子經過斯格明子時,由于電子自旋要與斯格明子內部的局域自旋發生耦合,使得電子的自旋方向來回地變化,最終電子可以獲得一個貝里相.如果這兩者的耦合作用比較強烈(絕熱條件),那么傳導電子的自旋總會受到一個垂直于運動方向的有效力,迫使它與局域自旋呈平行排列,并且這個有效力與斯格明子的拓撲數有關,文獻[2]稱此為“拓撲力”.從斯格明子的角度來講,由于非共面的磁矩排列會產生一個激發電磁場,從而使電子橫向漂移,形成一個可測量的霍爾電壓,最終實現斯格明子的探測[2,41,112](如圖14).
對于拓撲霍爾效應,已經有實驗研究發現在非中心對稱材料中存在較大的拓撲霍爾電壓,例如MnSi塊狀晶體[113?115],B20型的立方M nGe[116].最近,在低溫下的納米級FeGe霍爾棒結構中,Kanazawa等[117]測得拓撲霍爾電阻的離散變化,不僅首次證明了由斯格明子產生的激發電磁場的量子性,也證明了利用全電氣化的方案探測單個斯格明子的可行性.
4.2 磁阻效應
所謂磁電阻效應,是指材料的電阻率在外加磁場下會變化的現象,幾乎所有的金屬、合金或半導體都存在不同程度的磁阻效應.這是因為電子在外磁場中運動會受到洛倫茲力的作用,同霍爾效應一樣,電子的運動路徑發生偏轉或者做回旋運動,從而影響電子的輸運,即材料的電阻.

圖14 當電子流通過斯格明子時,傳導電子與斯格明子的運動情況[3,118]Fig.14.Schematic picture of skyrmion motion and associated physical phenomena under the flow of electrons[3,118].
與鐵磁態相比,當存在斯格明子時,由于非共線的自旋排列將導致電子態發生一定的變化;其次,重金屬基底會產生一個較大的自旋-軌道相互作用,將局域磁矩耦合到實空間方向,進一步調整電子的運動狀態.這兩種效應最終會一起影響隧穿電導或電阻[119].所以,若在讀出區域注入垂直于膜面的電流,可以利用磁阻效應檢測斯格明子.其中,磁阻效應又主要包括隧穿磁阻(tunneling magnetoresistance,TMR)效應、隧穿各向異性磁阻((tunneling)anisotropic magnetoresistance,(T)AMR)效應[120?123]和非共線磁阻(non-collinear magnetoresistance,NCMR)效應[124].而各向異性磁阻效應來源于材料的固有特性,其物理基礎是自旋-軌道耦合導致的散射截面不同,其大小主要取決于電流與磁場的相對取向.當電流與磁化方向平行時,電阻最大;當電流方向與磁化方向垂直時,電阻最小.由于各向異性磁電阻變化非常小,通常只有百分之幾的量級,很難辨別出不同自旋結構[122,123].因此,這種方案不適用于實際的斯格明子設備.
目前最有望用于斯格明子設備的探測方法是NCMR效應[124].這種效應是由于較大的磁化梯度產生的能帶結構變化而引起的,高度依賴于非共線的自旋結構[119,124],而與斯格明子的拓撲性質沒有直接的關系.在非共線自旋結構中,兩個自旋通道之間的混合將會導致電子能帶結構和局域態密度發生變化,實現斯格明子的電探測[124].相比于其他探測方案,例如TMR效應、反常霍爾效應或拓撲霍爾效應,基于NCMR效應的探測方法對非共線自旋結構(如斯格明子)尤為敏感,在鐵磁體系中,可以很容易地區分開非共線自旋態和常規磁疇.其次,利用NCMR效應來探測斯格明子,不需要在隧道結上提供磁反電極[124],從而使裝置的結構大大簡化,而且可以實現全電式的讀取數據,有效地降低能耗.此外,為了滿足實際應用的需要,NCMR效應也可以用于單個斯格明子逐一地有效檢測.Hanneken等[124]和Crum等[119]分別利用簡化的緊束縛(tight-binding,T-B)模型和密度泛函方法從理論上解釋了這一方案的物理原理.而且Hanneken等在Pd Fe/Ir(111)上利用NCMR效應成功地實現了斯格明子的探測.圖15為STM探針測得樣品上斯格明子相的情況,表明通過這種方式能探測到直徑約為3 nm的斯格明子.

圖15 (a)STM下恒定電流透視圖,用不同顏色說明d I/d U信號;黃色區域表示Pd Fe,紅色圓形區域表示磁性斯格明子;(b)兩個skyrmion的視圖,插圖表示沿著箭頭部分d I/d U的變化[124]Fig.15.(a)Perspective view of an STM constant-current image,color-coded with dI/d U signal;yellow areas indicate Pd Fe and red circular entities are magnetic skyrmions;(b)closer view of two skyrmions,d I/d U map,the inset presents a profile along the arrow[124].
5 斯格明子賽道存儲的優化設計
5.1 基于高PM A材料的賽道邊界設計
5.1.1 優化設計的理念與物理模型
目前,由電流驅動斯格明子的動力學研究已經取得了許多進展,然而,基于斯格明子的賽道存儲的研究仍面臨著一些問題.例如,當斯格明子在賽道上運動時,由于受到馬格努斯力的作用將會偏離賽道方向,發生橫向漂移(即斯格明子的霍爾效應),可能會使其在賽道邊緣處湮沒,造成信息的丟失.此外,若驅動電流太小,斯格明子會堵塞在塞道的末端.對于斯格明子的霍爾效應,通常是增加賽道邊界的勢壘,從而避免在邊緣處的湮沒[51,52,125,126]. 其中,Fook等[52]和Lai等[127]利用不同的方法調節賽道邊緣處的垂直磁晶各向異性來產生勢壘,限制斯格明子在賽道中的運動,解決了橫向漂移和堵塞等問題,并且斯格明子的運動速度也大大增加,提高了信息的讀取速度.
Fook等[52]提出了通過精確控制光離子輻射來調節賽道邊緣的PMA,使賽道中間區域的磁晶各向異性相比于兩側邊緣處的低一些.因此,當斯格明子在賽道中間區域運動時,磁矩的翻轉會遇到更低的阻力,從而可以順利地通過賽道而不發生湮沒.Fook等分別模擬了斯格明子在不加邊界勢壘和加了邊界勢壘的Co/Pt賽道上的運動情況.從模擬結果可以看出,這一新的賽道結構,既解決了斯格明子在邊緣處的湮沒問題,同時也大大提高了斯格明子在賽道上的運動速度.
Lai等[127]提出了一種更為簡單的改變賽道邊緣垂直磁晶各向異性的方法,即在Co/Pt賽道的兩個對稱邊緣添加具有高磁晶各向異性的材料,使得賽道的中間區域的磁晶各向異性低于賽道兩側邊緣的磁晶各向異性,防止了斯格明子在賽道邊緣處的湮沒,如圖16(a)所示.與Fook等提出的賽道模型相比,這一賽道模型不僅更容易調節賽道邊緣的磁晶各向異性,避免了高速運動的斯格明子在賽道邊緣處的湮沒和賽道末端的堵塞問題,而且斯格明子在此賽道上運動的速度比Fook等及其他課題組計算的速度要大得多.
5.1.2 邊界材料和電流密度大小的選取
Lai等[127]分別模擬了斯格明子在三種不同的高磁晶各向異性材料FePt,Nd2Fe14B和Sm Co5賽道上的運動,如圖16(b)—(d)所示.增加電流的驅動密度會使斯格明子成功地運動到賽道末端,但是也會增加馬格努斯力,導致朝向y方向的速度增加.因此,對于磁晶各向異性比較小的邊緣材料(比如FePt),若電流較小,斯格明子會堵塞在賽道末端;若電流較大,斯格明子會在賽道邊緣處湮沒.相比之下,如果邊界材料是磁晶各向異性比較大的材料(比如Nd2Fe14B和Sm Co5),則在大多數情況下,斯格明子都可以成功地通過塞道末端.只有當電流密度非常大或者當邊界材料非常窄時,斯格明子才會在賽道的上邊緣處湮沒.
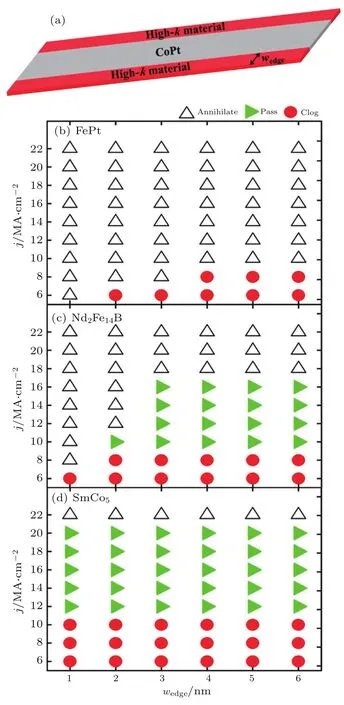
圖16 (a)斯格明子的賽道示意圖,其中間部分由CoPt材料制成,兩個對稱的邊緣部分由具有較高磁晶各向異性的材料制成,高磁晶各向異性材料的寬度由W edge表示;(b)—(d)在不同賽道邊緣寬度和電流密度的情況下,斯格明子運動狀態的計算相圖,空心三角形表示斯格明子受到馬格努斯力的作用,接觸到上邊緣而湮沒的狀態;綠色實心三角形表示斯格明子成功地通過賽道末端的狀態;紅色實心圓表示斯格明子堵塞在賽道末端的狀態[127]Fig.16.(a)Schematic of the proposed skyrmion racetrack,where the middle part is made of CoPt,whilst the two symmetrical edge parts are made of a material with a higher anisotropy with a width denoted by wedge.(b)–(d)Calcu lated phase diagrams for the motion of the skyrmions with various values of the racetrack edge width and the current density.The open triangles denote the phase where skyrmions will annihilate by touching the upper edge due to the Magnus force.The filled green triangle corresponds to the skyrmion phase at which it can reach the right end of the racetrack and pass th rough it.The red circle stands for the phase where skyrmions will clog at the right end of the racetrack[127].
表1是斯格明子在不同結構的Co/Pt賽道中沿x方向的運動速度和驅動電流密度的比較.圖16所采用的數據是表1中的第三項和第四項,1 MA/cm2的電流密度對應著斯格明子約10 m/s的運動速度.從表1中可以看出,改變賽道的結構及相關參數可有效地提高斯格明子的運動速度.例如,采用表1中的第五、第六項數據進行計算,斯格明子在改進后的賽道中的運動速度可以達到300 m/s,這遠大于在其他賽道中的速度.
5.2 反鐵磁耦合的雙層以及多層膜體系
對于斯格明子在電流驅動下所產生的斯格明子霍爾效應,Zhang等[129]提出了一種反鐵磁耦合的賽道來抑制斯格明子霍爾效應,對設計現實可用的斯格明子賽道存儲器具有一定的指導作用.
5.2.1 反鐵磁耦合的雙層膜體系
反鐵磁耦合的雙層膜體系如圖17所示,從上到下依次為頂部鐵磁層、絕緣層、底部鐵磁層和重金屬層.其中,頂部和底部鐵磁層都是垂直磁化,它們通過與重金屬層的反鐵磁交換相互作用而發生強耦合.當自旋極化電流注入頂部鐵磁層產生斯格明子時,底部鐵磁層也會同時產生一個相應的斯格明子,并且它們被夾層的反鐵磁耦合所聯系起來.像這樣的一對反鐵磁耦合的磁性斯格明子簡稱磁雙層斯格明子.對于驅動電流的注入,即使電流只注入底部的鐵磁層,頂層的斯格明子也會跟隨底層的斯格明子一起運動.因此,在自旋電流的驅動下,當夾層的反鐵磁交換耦合足夠大時,作用在頂部和底部鐵磁層上斯格明子的馬格努斯力大小相等、方向相反,相互抵消,斯格明子霍爾效應被完全壓制,從而使磁雙層斯格明子能在不碰到邊界的情況下向前運動.然而,當頂部和底部的鐵磁層退耦合或者反鐵磁交換耦合較小時,斯格明子霍爾效應不能被完全壓制,導致頂部和底部的斯格明子會分別向左和向右運動.當斯格明子碰到納米賽道邊緣時,斯格明子的結構就會被破壞,然后湮沒.

表1 斯格明子在不同賽道中沿x方向的運動速度v x和驅動電流密度j的比較Table 1.Comparison of skyrmion velocity v x and driving current j for different racetrack designed.

圖17 反鐵磁交換耦合雙層體系和雙層skyrmion的原理圖 (a)直徑為100 nm的AFM耦合雙層納米盤,用于雙層斯格明子的產生;(b)AFM耦合雙層納米賽道(500 nm×50 nm×3 nm)用于研究垂直于平面(CPP)的電流驅動雙層斯格明子的運動;(c)AFM耦合雙層納米賽道(500 nm×50 nm×3 nm)用于研究平面電流(CIP)驅動的雙層斯格明子的運動.在所有模型中,頂部FM層、底層FM層和絕緣間隔層的厚度均為1 nm,頂部FM層的初始狀態幾乎是自旋向上(指向+z),而底層FM層的初始狀態幾乎是自旋向下的(指向?z);(d)AFM耦合的納米盤中一對斯格明子(即雙層斯格明子)的圖解;(e)雙層斯格明子的側視圖;彩色刻度表示磁化強度的面外分量[129]Fig.17.Schematics of the antiferromagnetically exchange-coupled bilayer systems and the bilayer-skyrmion:(a)The AFM-coupled bilayer nanodisk with a diameter of 100 nm for bilayer-skyrmion creation;(b)the AFM-coupled bilayer nanotrack(500 nm×50 nm×3 nm)for the study of the motion of a bilayer-skyrmion driven by the current perpend icular to the plane(CPP);(c)the AFM-coupled bilayer nanotrack(500 nm×50 nm×3 nm)for the study of the motion of a bilayer-skyrmion driven by the in-plane current(CIP);in all the models,the thickness of both the top FM layer,the bottom FM layer and the insulating spacer are equal to 1 nm;the initial state of the top FM layer is almost spin-up(pointing along+z)and that of the bottom FM layer is almost spin-down(pointing along?z);(d)illustration of a pair of skyrmions(that is the bilayer-skyrmion)in an AFM-coupled nanodisk;(e)side view of the bilayer-skyrmion.The colour scale represents the out-of-plane component of the magnetization[129].
5.2.2 反鐵磁耦合的多層膜體系
如圖18所示,對于單層的反鐵磁耦合賽道,是由一個鐵磁層和一個位于鐵磁層下面的重金屬底層構成.而N層的反鐵磁賽道[130]包括N個垂直磁化的鐵磁層和一個位于最下面的重金屬底層,這N個鐵磁層之間都有絕緣層.在N(N>2)層的反鐵磁賽道中,相鄰的鐵磁層通過鐵磁層/絕緣層/鐵磁層的界面發生反鐵磁交換耦合,所以相鄰鐵磁層的磁化方向是反平行.模擬結果顯示,在電流驅動過程中,單層(N=1)和三層(N=3)反鐵磁耦合賽道中的斯格明子由于霍爾效應的作用發生明顯的橫向移動.而雙層(N=2)和四層(N=4)反鐵磁耦合賽道中的斯格明子沿著賽道中心線運動,斯格明子霍爾效應并沒有得到表現.這說明只有在N為偶數的N層反鐵磁賽道中,霍爾效應被完全抑制,斯格明子才能沿著驅動電流的方向做直線運動.此外,模擬結果表明斯格明子運動的橫向速度vx與N近似呈反比關系[130].
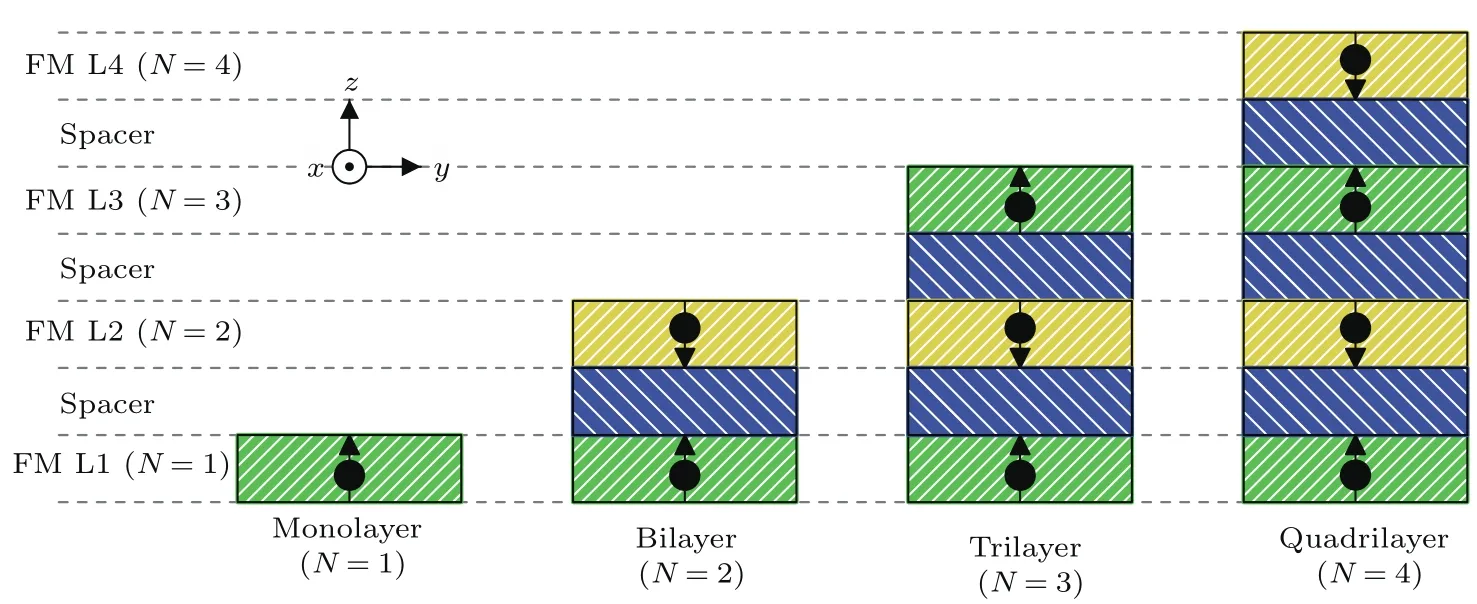
圖18 包括FM單分子層在內的雙層SAF,三層SAF和四層SAF賽道的仿真模型原理圖[130]Fig.18.Schematics of the simulation models including the FM monolayer,bilayer SAF,trilayer SAF,and quadrilayer SAF racetracks[130].
5.3 雙賽道模型
對于典型的斯格明子的賽道存儲,以斯格明子的存在與否代表二進制數據“1”和“0”,理想狀態下,相鄰兩個二進制數據之間的距離保持不變,如圖19(a),在賽道上每隔相同的距離編碼一個數據,存在斯格明子,則為“1”,反之為“0”.然而在實際情況中,由于環境帶來的各種熱擾動和存儲設備高頻運行時所產生的噪音,將會影響賽道上攜帶信息的斯格明子鏈重新分布,導致相鄰兩數據間的距離發生變化,從而使信息編碼有誤.比如,要想連續編碼多個二進制數據“0”,則在賽道上就會有一段較長的距離沒有斯格明子,而考慮到實際的各種干擾,當斯格明子運動時,它們之間的距離發生變化,因此無法準確地確定“0”的個數,這就可能造成信息的部分丟失.
基于以上討論,Müller等[131]提出了一種新的賽道模型,綜合考慮了信息的二進制編碼及連續驅動,很好地解決了上面所提到的問題.其基本模型是在一條賽道上再增加一個斯格明子通道,構成上下兩層的雙賽道,并以一個較高的能量勢壘將它們分開,二進制數據全部編碼在斯格明子中.與原始的單賽道不同,在這種雙賽道中,數據的編碼與斯格明子之間的距離沒有關系,而是根據斯格明子所在的通道來區分“0”和“1”,即根據斯格明子到賽道中心的位移來判斷,當斯格明子在賽道中心的上方時代表“0”,反之,則為“1”.基于此,在該模型中,信息的編碼將不再受斯格明子之間的距離影響,可以很好地抵抗外界的熱擾動,而且當加入驅動電流時,斯格明子鏈仍然可以沿著賽道加速前進.此外,兩個賽道之間靠得足夠近,以至于兩賽道上的斯格明子之間存在較大的相互排斥作用,從而維持自身的運動軌跡,避免斯格明子在兩賽道上互相穿插,影響信息的存儲.
Lai等[132]也對雙賽道進行了研究,與Müller等[131]的模型相同的是,都以斯格明子所在的不同通道來編碼二進制數據“0”和“1”(如圖19(b)),取代了原始的單賽道中以斯格明子的有無來編碼二進制數據的方法.無論是數據位“1”,還是“0”,我們都能在賽道中探測到斯格明子,從而可以克服單通道賽道中由于數據位“0”的個數的不明確而造成的信息失真的問題.因此,這種數據編碼的方法顯得更加穩定和可靠.而兩者不同的是,Lai等所考慮的雙賽道是兩個斯格明子通道水平排列,并由磁晶各向異性比較高的材料將其隔開,使斯格明子在各自的通道上運動.

圖19 基于斯格明子的不同賽道模型及數據表示 (a)單賽道的數據表示;(b)雙賽道模型及其數據表示[132]Fig.19. Different skyrmion-based racetrack modes and data representation: (a)Rep resents a singlelane racetrack;(b)rep resent the two-lane racetrack modes[132].
Lai等[132]運用三維模擬軟件OOMMF,模擬了斯格明子在兩個賽道中同時運動的情況,研究了斯格明子在各自賽道中運動而不發生橫穿行為的條件.模擬結果表明:一方面,斯格明子在雙通道的賽道中運動時,驅動電流越大,兩通道之間的距離越小,斯格明子的橫穿行為就越容易發生,但增加兩通道之間材料的磁晶各向異性可以形成較高的能量勢壘,從而阻止下側通道的斯格明子的橫向穿越,到達上側通道;此外,當間隔材料的磁晶各向異性特別大或者特別小時,兩通道之間的距離對斯格明子運動狀態的調制作用非常微弱,只有取合適值時,這種調制作用才比較大;另一方面,通過研究基于不同的磁晶各向異性值,斯格明子在不同DMI常數和電流密度下的運動狀態,驅動電流越大,DMI常數D越大,斯格明子的橫穿行為就越容易發生;同樣,與間隔材料的磁晶各向異性也有關[132].由于斯格明子的尺寸由DMI和海森伯交換相互作用共同決定(lD=2A/D)[133],當交換常數A不變時,D增大,斯格明子的尺寸增大.因此,D值越大時,下側通道中的斯格明子越容易越過中間的高PMA部分,進入到上側通道.顯然,這一結果剛好與數值模擬符合.
此外,Kang等[134]也曾提出互補的斯格明子賽道結構,利用一個場控的Y型結決定斯格明子的去向.在他們的模型中同樣也是根據斯格明子所在的不同賽道來區分二進制數“0”和“1”,從而提高數據信息的穩定性和有效性.
6 結 論
斯格明子的賽道存儲這一概念自提出以來,吸引了大量的科研人員對其進行深入的研究,因此,近幾年得到了迅猛的發展.結合最新的研究成果,本文就斯格明子在賽道上的產生、運動、讀出三個方面進行了較為詳細的綜述.斯格明子的產生通常利用自旋極化電流、外加磁場、局部加熱等方法來實現.這樣產生的斯格明子不僅能穩定存在于幾十開爾文的低溫下,在某些情況下也可以在室溫下穩定存在.其次,對于斯格明子在賽道上的運動,注入自旋極化電流是較為常用的驅動方式,分為面內注入和垂直膜面注入.無論采取哪種注入方式,斯格明子在運動過程中都會同時擁有橫向和縱向兩個速度.相比之下,垂直膜面注入時,驅動效率更高.此外,在利用極化電流所產生的自旋轉移矩驅動斯格明子時,由于斯格明子的霍爾效應,可能會導致存儲信息的丟失,從而影響賽道存儲的有效性.增加賽道邊緣的勢壘,或者利用反鐵磁耦合的雙層膜體系都可以較好地解決這一問題.除了自旋極化電流,壓控磁各向異性效應作為一種新的電處理方法也可以對斯格明子進行操控.它通過調節外加電場的強度來改變局域的磁晶各向異性強度,在電流的協助下有效地控制斯格明子的運動方向.另外,對于斯格明子在賽道上的讀出,本文主要討論了利用拓撲霍爾效應和非共線磁阻效應兩種方案探測斯格明子.這兩種方法都可以實現純電探測單個斯格明子,這也正是當前大多數斯格明子自旋設備發展所需要的.
目前,關于斯格明子賽道存儲的研究還面臨一些挑戰.首先,很多研究僅停留在理論階段,在實驗上還面臨著一定的挑戰.絕大多數的理論工作都采用了理想化模型,假設材料很均勻、純凈,而實際情況下,材料都含有一定量的雜質,這些無序結構很可能會影響斯格明子的成核、運動、探測等操控,從而使實驗結果與理論計算結果出現偏差.其次,大多數理論和實驗中所研究的斯格明子的尺寸都在100 nm左右,要充分發揮斯格明子尺寸小、存儲密度高的優點,有必要將斯格明子的尺寸降低到10 nm左右.此外,為了使斯格明子達到100 m/s左右的穩定速度,目前大多數賽道存儲的理論設計所采用的電流密度量級為1011A/m2.這一電流密度與疇壁的賽道存儲相比優勢還不顯著,還沒有充分發揮斯格明子塞道存儲節能的優勢.電流密度過大還有一個很大的弊端,它會產生較大的焦耳熱從而燒壞器件,對實際應用帶來一些限制.最后,如何便捷有效地抑制賽道存儲中的斯格明子霍爾效應,依然是一個很大的挑戰.

