面向文件存儲(chǔ)的虛擬網(wǎng)絡(luò)映射算法

陳 晨，鄭 烇，王志臻，田洪亮

(1. 中國(guó)科學(xué)技術(shù)大學(xué) 信息科學(xué)技術(shù)學(xué)院，安徽 合肥 230027； 2. 中興通訊股份有限公司，廣東 深圳 518057)

0 引言

隨著網(wǎng)絡(luò)技術(shù)的發(fā)展，為了解決當(dāng)前互聯(lián)網(wǎng)“僵化”問(wèn)題，研究者提出了網(wǎng)絡(luò)虛擬化技術(shù)，它可以為用戶提供多樣化服務(wù)[1-2]，也是構(gòu)建新一代網(wǎng)絡(luò)體系架構(gòu)的重要支撐[3]。虛擬網(wǎng)絡(luò)映射是實(shí)現(xiàn)網(wǎng)絡(luò)虛擬化的關(guān)鍵環(huán)節(jié)，其目的是在滿足虛擬網(wǎng)絡(luò)請(qǐng)求(Virtual Network Request, VN請(qǐng)求)的前提下，將虛擬網(wǎng)絡(luò)以最小化成本映射到物理網(wǎng)絡(luò)上，實(shí)現(xiàn)網(wǎng)絡(luò)資源的高效利用[4]。

虛擬網(wǎng)絡(luò)映射問(wèn)題包括節(jié)點(diǎn)映射和鏈路映射兩個(gè)問(wèn)題，一般在節(jié)點(diǎn)映射階段采用啟發(fā)式算法，然后在確定源和目的節(jié)點(diǎn)的基礎(chǔ)上，將鏈路映射轉(zhuǎn)化為最小費(fèi)用流問(wèn)題，采用最短路徑算法完成映射。根據(jù)兩個(gè)問(wèn)題是否獨(dú)立進(jìn)行，可將虛擬網(wǎng)絡(luò)映射分為同階段映射和兩階段映射[5]。同階段映射中，在映射虛擬節(jié)點(diǎn)的同時(shí)考慮鏈路映射，如D-ViNE算法[6]和vnmFlib算法[7]。兩階段映射中，節(jié)點(diǎn)映射和鏈路映射獨(dú)立進(jìn)行，先映射節(jié)點(diǎn)后映射鏈路，如NA-PVNM算法[8]。

在已有的研究中，VN請(qǐng)求大都是對(duì)節(jié)點(diǎn)計(jì)算資源和鏈路帶寬資源的需求。本文研究的是將含有文件需求的VN請(qǐng)求映射到有存儲(chǔ)的物理網(wǎng)絡(luò)上，VN請(qǐng)求不僅包括以上的需求，還包括對(duì)節(jié)點(diǎn)存儲(chǔ)資源的需求。因?yàn)槲锢砉?jié)點(diǎn)上可能存在請(qǐng)求文件的存儲(chǔ)，所以當(dāng)請(qǐng)求命中時(shí)，該節(jié)點(diǎn)流向下游的流量減少。該情況可以轉(zhuǎn)化為節(jié)點(diǎn)的損耗問(wèn)題，即廣義最小費(fèi)用流問(wèn)題[9]。本文提出了一種基于節(jié)點(diǎn)連通性和廣義網(wǎng)絡(luò)單純形法的虛擬網(wǎng)絡(luò)映射算法——S-VNM算法，在節(jié)點(diǎn)映射階段綜合考慮節(jié)點(diǎn)位置和鏈路映射的映射成本兩個(gè)因素，從而減小搜索空間，降低映射成本。通過(guò)實(shí)驗(yàn)仿真驗(yàn)證了該算法的有效性和良好性能。

1 相關(guān)技術(shù)

1.1 虛擬網(wǎng)絡(luò)映射問(wèn)題描述

1.1.1虛擬網(wǎng)絡(luò)映射模型

在虛擬網(wǎng)絡(luò)映射模型中[10]，物理網(wǎng)絡(luò)由一個(gè)無(wú)向圖GS=(NS,ES,CS,BS) 表示，其中NS代表物理節(jié)點(diǎn)，ES代表物理鏈路，CS代表物理節(jié)點(diǎn)的資源，BS代表物理鏈路的資源。本文研究的是在有存儲(chǔ)的物理網(wǎng)絡(luò)上進(jìn)行虛擬網(wǎng)絡(luò)映射，因此，CS代表的節(jié)點(diǎn)資源包括節(jié)點(diǎn)計(jì)算資源和存儲(chǔ)資源。VN請(qǐng)求也可以表示為GV=(NV,EV,CV,BV) ,各字符代表的意義與物理網(wǎng)絡(luò)類似。虛擬網(wǎng)絡(luò)映射過(guò)程用映射函數(shù)M(GV,GS)來(lái)表示：

M(GV,GS) :

(NV,EV,CV,BV) →(NS,ES,CS,BS)

(1)

1.1.2約束條件

虛擬節(jié)點(diǎn)映射時(shí)要滿足物理節(jié)點(diǎn)不可分拆、計(jì)算資源及存儲(chǔ)資源的約束，表示如下：

M(i) ≠M(fèi)(j), ?i,j∈NV且i≠j

(2)

CSC(M(nV))≥CVC(nV), ?nV∈NV

(3)

CSS(M(nV))≥CVS(nV), ?nV∈NV

(4)

其中，式(2)表示每個(gè)虛擬節(jié)點(diǎn)只能映射到單個(gè)且互不相同的物理節(jié)點(diǎn)上；式(3)和式(4)分別表示物理節(jié)點(diǎn)可用的計(jì)算資源和存儲(chǔ)資源不少于虛擬節(jié)點(diǎn)的所需。

定義虛擬鏈路lV=(i,j) 映射到物理鏈路上的路徑集合為PM(lV) 。定義路徑p∈PM(lV) 上為虛擬鏈路分配的帶寬為B(lV,p)。虛擬鏈路映射時(shí)約束如下：

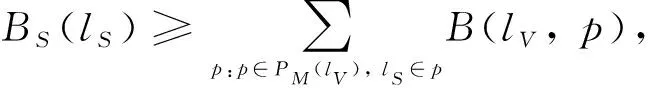
(5)

式(5)表示鏈路映射過(guò)程中物理鏈路lS上有足夠的帶寬資源BS(lS)。

1.1.3性能指標(biāo)

虛擬網(wǎng)絡(luò)映射問(wèn)題是節(jié)點(diǎn)和鏈路資源約束下的優(yōu)化問(wèn)題，主要的性能指標(biāo)有映射成本、映射時(shí)間[11]及VN請(qǐng)求的接受率等。本文以映射成本和映射時(shí)間作為評(píng)價(jià)算法的性能指標(biāo)。

虛擬網(wǎng)絡(luò)的映射成本包括節(jié)點(diǎn)映射成本和鏈路映射成本。總映射成本C(GV) 表示如下：

(6)

其中，CNC(nV) 代表節(jié)點(diǎn)映射的計(jì)算成本，CNS(nV) 代表節(jié)點(diǎn)映射的存儲(chǔ)成本，CE(lV) 代表鏈路映射成本。

1.2 廣義最小費(fèi)用流問(wèn)題描述

在一些實(shí)際的網(wǎng)絡(luò)流問(wèn)題中，有些節(jié)點(diǎn)和弧并不滿足流量平衡條件，使得經(jīng)典的網(wǎng)絡(luò)模型無(wú)法對(duì)其描述，現(xiàn)有研究將其稱為廣義費(fèi)用流問(wèn)題[9]。

1.2.1廣義最小費(fèi)用流問(wèn)題

令G=(N,A) 為一個(gè)有向網(wǎng)絡(luò)，其中N為節(jié)點(diǎn)的集合，A為弧的集合。對(duì)于任意的弧 (i,j)∈A，令xij表示從節(jié)點(diǎn)i出發(fā)沿著弧 (i,j) 行進(jìn)的流量，uij為xij的上界，即：

0 ≤xij≤uij,(i,j)∈A

(7)

令 0<μij<1 為弧 (i,j) 上的損耗因子，并假設(shè)當(dāng)沿著弧 (i,j) 從節(jié)點(diǎn)i發(fā)送一個(gè)單位流量時(shí)，有μij個(gè)單位流量到達(dá)節(jié)點(diǎn)j。對(duì)于節(jié)點(diǎn)i∈N，定義E(i)和L(i) 分別為“進(jìn)入”和“離開”該節(jié)點(diǎn)的弧的集合，即：

E(i)={(j,i)∈A:j∈N} 且

L(i)={(i,j)∈A:j∈N}

(8)

1.2.2各節(jié)點(diǎn)約束條件

對(duì)于源節(jié)點(diǎn)S-節(jié)點(diǎn)，令NS表示所有S-節(jié)點(diǎn)的集合。對(duì)每一個(gè)i∈NS，有E(i)=φ，且有一個(gè)輸入流xi使得：

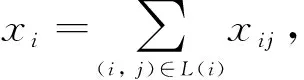
(9)

對(duì)于轉(zhuǎn)運(yùn)節(jié)點(diǎn)O-節(jié)點(diǎn)，滿足：

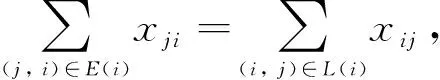
(10)

對(duì)于分配節(jié)點(diǎn)D-節(jié)點(diǎn)，輸出弧上的流量與進(jìn)入弧上的流量成比例，滿足：

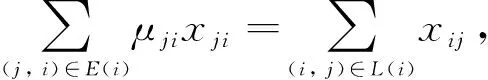
(11)

對(duì)于目的節(jié)點(diǎn)T-節(jié)點(diǎn)，對(duì)每一個(gè)i∈NT，有L(i)=φ，且有一個(gè)輸出流xi使得：

(12)

2 本文算法

本節(jié)詳細(xì)介紹了S-VNM算法，該算法實(shí)現(xiàn)了將含有文件需求的VN請(qǐng)求映射到有存儲(chǔ)的物理網(wǎng)絡(luò)上。其分為三個(gè)階段：(1) 虛擬節(jié)點(diǎn)排序；(2) 虛擬節(jié)點(diǎn)映射；(3) 虛擬鏈路映射。

2.1 虛擬節(jié)點(diǎn)排序

一個(gè)具體的VN請(qǐng)求包含多個(gè)虛擬節(jié)點(diǎn)，由于物理網(wǎng)絡(luò)資源有限，對(duì)資源需求越大的節(jié)點(diǎn)越難映射成功，因此優(yōu)先映射該類節(jié)點(diǎn)。同時(shí)，為了保證映射的相關(guān)性，在進(jìn)行下一個(gè)虛擬節(jié)點(diǎn)映射時(shí)，優(yōu)先選擇與已映射的虛擬節(jié)點(diǎn)集合有關(guān)聯(lián)的節(jié)點(diǎn)。

定義虛擬節(jié)點(diǎn)的需求CR(nV) 如下：

(13)

其中，CC(nV) 代表虛擬節(jié)點(diǎn)nV的計(jì)算資源需求，CS(nV) 代表nV的存儲(chǔ)資源需求，L(nV)代表所有與nV相關(guān)聯(lián)的鏈路集合，B(l) 代表與nV相關(guān)聯(lián)的鏈路所需的帶寬資源。

2.2 虛擬節(jié)點(diǎn)映射

本文提出的虛擬節(jié)點(diǎn)映射算法是基于物理節(jié)點(diǎn)連通性和映射總成本實(shí)現(xiàn)的。

定義與虛擬節(jié)點(diǎn)nV相關(guān)聯(lián)的已映射虛擬節(jié)點(diǎn)在物理網(wǎng)絡(luò)中的映射節(jié)點(diǎn)集合為M。定義物理節(jié)點(diǎn)ns與集合M的連通性為Nrank(ns)：

Nrank(ns)=

(14)

其中，CC(ns) 代表物理節(jié)點(diǎn)ns的可用計(jì)算資源，CS(ns) 代表ns的可用存儲(chǔ)資源，Cavailable(nt,ns) 代表物理節(jié)點(diǎn)nt與ns之間的可行流，D(nt,ns) 代表兩節(jié)點(diǎn)之間的距離。

按照節(jié)點(diǎn)連通性將物理節(jié)點(diǎn)由大到小排序后，選擇排序靠前的節(jié)點(diǎn)作為待選節(jié)點(diǎn)。然后，對(duì)待選節(jié)點(diǎn)進(jìn)行節(jié)點(diǎn)映射和鏈路映射，根據(jù)每一次映射結(jié)果，統(tǒng)計(jì)節(jié)點(diǎn)的映射成本和所有相關(guān)鏈路的映射成本作為效用函數(shù)Ctotal(ns)，以此來(lái)評(píng)價(jià)物理節(jié)點(diǎn)ns，最終選擇效用函數(shù)最小的節(jié)點(diǎn)作為映射節(jié)點(diǎn)。效用函數(shù)Ctotal(ns) 表示如下：

(15)

其中，CNC(nV) 代表節(jié)點(diǎn)映射的計(jì)算成本，CNS(nV) 代表節(jié)點(diǎn)映射的存儲(chǔ)成本，CE(nt,ns) 代表映射到物理節(jié)點(diǎn)ns的最小鏈路映射成本。

2.3 虛擬鏈路映射

在虛擬節(jié)點(diǎn)映射時(shí)，節(jié)點(diǎn)映射成本易求出，但如何求最小鏈路映射成本的問(wèn)題可轉(zhuǎn)化為最小費(fèi)用流問(wèn)題。

本文的VN請(qǐng)求含有文件需求，因此在映射的過(guò)程中，應(yīng)考慮該情況：如果當(dāng)下的映射節(jié)點(diǎn)與已映射節(jié)點(diǎn)之間的路徑上存在含有該文件的節(jié)點(diǎn)，當(dāng)請(qǐng)求命中時(shí)，有該文件的節(jié)點(diǎn)類似于分配節(jié)點(diǎn)D-節(jié)點(diǎn)，需留下該文件的流而將其他需求的流送出。由此可見(jiàn)，求解鏈路映射成本問(wèn)題可轉(zhuǎn)化為廣義最小費(fèi)用流問(wèn)題。

虛擬鏈路映射成本問(wèn)題的模型可以表示為：

(16)

s.t.x∈F

其中，x是在給定網(wǎng)絡(luò)G=(N,A) 的弧集上的可行流，F(xiàn)是所有滿足式(7)～(12)的可行流的集合，Cij是從節(jié)點(diǎn)i出發(fā)的單位流量沿弧 (i,j) 到達(dá)節(jié)點(diǎn)j所產(chǎn)生的費(fèi)用。

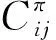
(17)

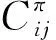
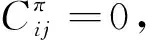
(18)

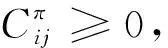
(19)

則 (F,L) 為最優(yōu)結(jié)構(gòu)。

本文提出的虛擬鏈路映射算法的核心思想是：

(1) 生成初始基本可行結(jié)構(gòu) (F,L)。

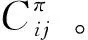
(3) 檢驗(yàn)式(19)和式(20)所示的最優(yōu)條件。如果所有的最優(yōu)性條件全都滿足，則算法停止；否則，選擇一條不滿足最優(yōu)性條件的弧 (k,l) 作為進(jìn)基弧。

(4) 在進(jìn)基弧 (k,l) 上增加適當(dāng)?shù)牧髁浚?jì)算基本可行圖上各弧上流量的調(diào)整量，更新基本可行解x和基本可行結(jié)構(gòu) (F,L)，轉(zhuǎn)步驟(2)。

由此，可求出基本可行解x，進(jìn)而計(jì)算出虛擬鏈路映射的最小成本，再計(jì)算出待選節(jié)點(diǎn)的效用函數(shù)Ctotal(ns)，選擇該值最小的節(jié)點(diǎn)作為映射節(jié)點(diǎn)，最終完成虛擬網(wǎng)絡(luò)映射。

算法S-NVM

輸入：VN請(qǐng)求(NV,EV)，物理網(wǎng)絡(luò)(NS,ES)；

輸出：虛擬映射M(GV,GS)。

1.M=φ，Di=φ，i=0，step=0，N

// 初始化

//Di代表待選物理節(jié)點(diǎn)的集合

2. for allnV∈NV

//虛擬節(jié)點(diǎn)排序

3. count theCR(nV) ofnV

4. end for

5. arrangenVin descending according toCR(nV)

7. if (M=φ)

// 第一個(gè)虛擬節(jié)點(diǎn)映射

11. end if

12. else

// 虛擬節(jié)點(diǎn)和虛擬鏈路映射

// 選擇與上一個(gè)映射的虛擬節(jié)點(diǎn)有關(guān)聯(lián)的節(jié)點(diǎn)

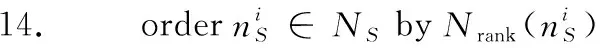
// 選擇按照連通性大小排序后的前N個(gè)節(jié)點(diǎn)

17. step++

19. end for

23. end else

24.i++

25. end for

3 實(shí)驗(yàn)與結(jié)果分析

實(shí)驗(yàn)通過(guò)MATLAB進(jìn)行仿真評(píng)估。采用GT-ITM拓?fù)洚a(chǎn)生器隨機(jī)生成物理網(wǎng)絡(luò)和虛擬網(wǎng)絡(luò)請(qǐng)求。本文將D-ViNE算法和vnmFlib simple算法作為對(duì)照，從映射成本和算法運(yùn)行時(shí)間兩方面進(jìn)行比較。

物理網(wǎng)絡(luò)包含60個(gè)節(jié)點(diǎn)，150條鏈路。物理節(jié)點(diǎn)的可用計(jì)算和存儲(chǔ)容量服從[50,150]均勻分布，單位成本服從[1,5]均勻分布。物理鏈路可用帶寬容量服從[1,100]均勻分布，單位成本服從[1,10]分布。虛擬網(wǎng)絡(luò)節(jié)點(diǎn)個(gè)數(shù)服從[3,15]均勻分布，任意兩個(gè)虛擬節(jié)點(diǎn)之間以0.5的概率連接，虛擬節(jié)點(diǎn)和虛擬鏈路需求服從[10,50]均勻分布。μij=0.7。

基于以上仿真環(huán)境，運(yùn)行三種映射算法，結(jié)果如圖1和圖2所示。

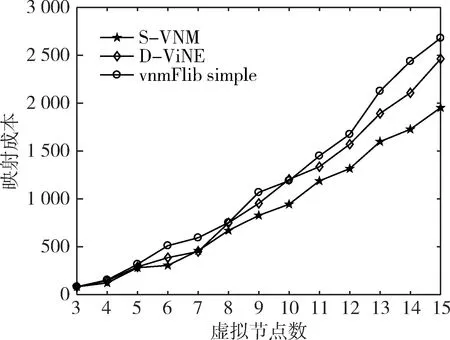
圖1 映射成本隨虛擬節(jié)點(diǎn)數(shù)變化趨勢(shì)圖

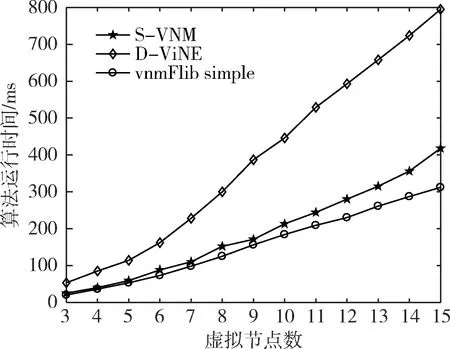
圖2 算法運(yùn)行時(shí)間隨虛擬節(jié)點(diǎn)數(shù)變化趨勢(shì)圖

實(shí)驗(yàn)結(jié)果表明，S-VNM算法整體上比其他兩種算法有優(yōu)勢(shì)。在映射成本方面，S-VNM算法性能最好，因?yàn)樵谒阉鹘饪臻g過(guò)程中每次都取映射成本最小的節(jié)點(diǎn)作為映射結(jié)果。在運(yùn)行時(shí)間方面，S-VNM算法優(yōu)于D-ViNE算法，這是因?yàn)镾-VNM算法在映射時(shí)選擇連通性較大的節(jié)點(diǎn)進(jìn)行映射，減小搜索空間，從而降低運(yùn)行時(shí)間。但S-VNM在運(yùn)行時(shí)間方面劣于vnmFlib simple算法，這是因?yàn)関nmFlib simple算法直接使用區(qū)間內(nèi)的最大跳數(shù)作為路徑條數(shù)約束，雖沒(méi)有減小搜索空間，但算法復(fù)雜度低，所以運(yùn)行時(shí)間短。

4 結(jié)論

本文提出一種啟發(fā)式搜索和基于廣義網(wǎng)絡(luò)單純形法的虛擬網(wǎng)絡(luò)映射算法——S-VNM算法，其實(shí)現(xiàn)了將含有文件需求的VN請(qǐng)求映射到有存儲(chǔ)的物理網(wǎng)絡(luò)上。S-VNM算法在節(jié)點(diǎn)映射階段把物理節(jié)點(diǎn)之間的連通性作為篩選標(biāo)準(zhǔn)，虛擬節(jié)點(diǎn)的映射成本作為效用函數(shù)，與傳統(tǒng)算法相比減小了搜索空間，降低了映射成本。在鏈路映射階段采用廣義網(wǎng)絡(luò)單純形法，與最短路徑算法相比降低了映射的時(shí)間復(fù)雜度。實(shí)驗(yàn)結(jié)果表明，在綜合考慮映射成本和算法運(yùn)行時(shí)間的情況下，本文提出的算法性能最優(yōu)。