基于ANSYS的氣氛燒結爐動態溫度場研究
李 強,王 璐
(西安理工大學 自動化與信息工程學院,陜西 西安710048)
0 引言
氣氛燒結爐是粉末冶金行業的關鍵設備。燒結爐在進行產品燒結時的溫度分布會直接影響產品質量。因此,對燒結爐內溫度場的精確控制是確保粉末冶金燒結成功的重要前提。采用ANSYS仿真軟件建立仿真模型[1-3],對多種結構的燒結爐進行溫度場動態分析[4-6]。研究爐體結構和工藝參數對燒結爐內溫度場分布規律的影響,從而對爐體設計結構[7]和工藝參數[8]的選用進行指導,可以大幅度降低研制成本,同時提高燒結爐研制效率。
本課題運用有限元分析的思想,利用ANSYS軟件對燒結爐建立仿真模型[9],通過改變加熱體形狀、爐襯結構等建立新的燒結爐仿真模型進行溫度場仿真,模擬出接近真實的溫度分布。觀察不同結構下燒結爐溫度場的變化情況,從而對現實中的工業加熱石墨加熱體的設計提供有效的優化指導。
1 有限元分析
1.1 氣氛燒結爐結構簡化
氣氛燒結爐主要由爐頂、爐底、爐墻、爐殼以及加熱元件等組成。其中加熱元件采用石墨加熱體,爐墻及爐頂均為三層,選用相同的隔熱層材料,從內至外分別為電極石墨(或硬質碳氈)、碳氈、硅酸鋁纖維;爐殼為兩層中間夾有循環水不銹鋼鋼板;隔熱層(電極石墨層或硬質碳氈層)并未與加熱元件直接接觸,它們之間還隔有用于絕緣的氮氣層;爐底為莫來石搗打層。燒結爐結構示意見圖1。
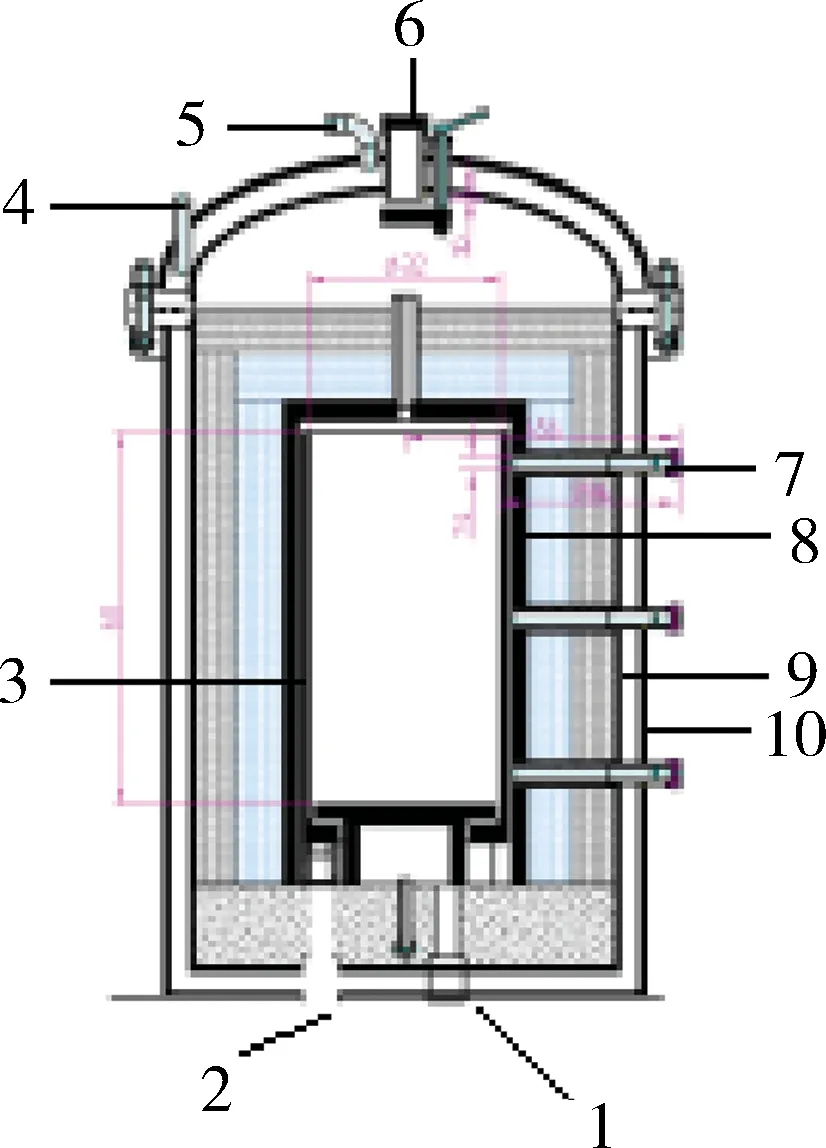
1.電極 2.抽真空系統 3.石墨加熱體 4.進水口 5.出水口 6.觀察口 7.熱電偶插入口 8.絕緣層 9.循環水層 10.外鋼板圖1 燒結爐結構圖
1.2 ANSYS有限元分析
燒結爐內溫度傳輸通過傳導、對流和輻射散失到周圍介質中去。為了便于計算作以下假設:(1)材料各向同向;(2)材料參數密度、比熱容為常數;(3)環境溫度不變,為室溫22 ℃;(4)石墨加熱體溫度分布均勻。其熱傳導傳遞的凈熱量可用傅里葉定律計算:
(1)
式中,Q為熱流率,λ為材料的導熱系數,A為導熱面積,dT/dn為溫度梯度。
其熱對流遵循的凈熱量可用牛頓冷卻公式計算:
Q=Ah(ts-tf)
(2)
式中,h表示對流換熱系數,ts為固體表面溫度,tf為流體溫度。
熱輻射凈熱量可用斯蒂芬-玻爾茲曼定律方程計算:
(3)
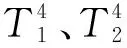
氣氛燒結爐的物理模型是具有一定初始條件和邊界條件的瞬態熱傳導,其導熱方程為:
(4)
式(4)描述了加熱體內部進行熱傳導時各點溫度的變化規律。
在ANSYS中,若只考慮模型表面對周圍環境的輻射以及表面之間的相互輻射,則輻射熱量可以簡化為式(5):
(5)
其中,Qi為i表面的輻射熱流率,εi為i表面的有效輻射率,Fij為輻射角系數(視角因子),Ai、Aj分別表示i表面和j表面的面積,Ti、Tj分別表示i表面和j表面的絕對溫度。
1.3 有限元模型及材料參數
1.3.1建立模型
(1)均勻溫度場仿真模型
在均勻溫度場燒結爐結構中,加熱體的結構均設計為圓筒形,設置燒結爐的環境溫度為22 ℃,電功率為90 kW,其模型如圖2所示。
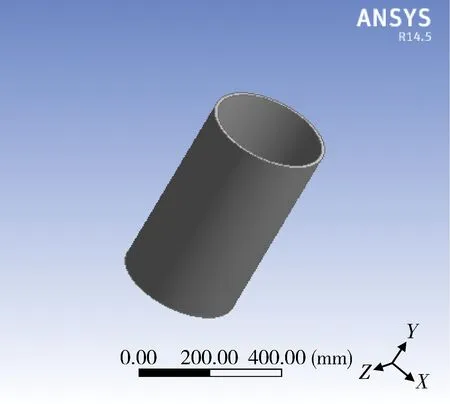
圖2 均勻加熱體模型
在本設計中,加熱元件與各層爐墻均為圓筒狀,在理想狀態下,石墨加熱體向爐膛與爐墻的熱輻射是均勻的,爐襯向外的傳熱也是均勻的,所以爐膛內的溫度也會均勻分布。在此基礎上改變爐襯結構建立結構一、結構二、結構三模型[10]。
(2)梯度溫度場仿真模型
將加熱體結構設計為階梯式,共分為3段(即將爐膛內加熱區分為3區),每段仍為圓筒狀,高度均為200 mm,第一段(接近爐底)厚度為20 mm,第二段(中間段)厚度為15 mm,第三段(接近爐頂)厚度為10 mm。在此基礎上改變爐襯結構建立結構四、結構五、結構六模型。階梯式加熱體模型如圖3所示。
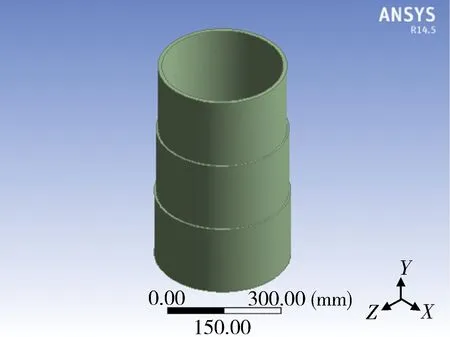
圖3 梯狀加熱體模型
1.3.2參數設置
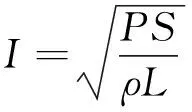

表1 材料屬性
結爐中主要的熱傳遞方式為熱傳導與熱輻射。在ANSYS熱分析中,若表面互相接觸則默認為會發生傳熱,故不需要再單獨設置熱傳導參數。根據表2所示參數即可為燒結爐系統施加熱輻射載荷。

表2 熱輻射發射率
最后通過分析模塊中的相應設置進行溫度場的求解。
2 溫度場仿真結果分析
2.1 靜電場分析仿真結果
均勻溫度場,因為其3種結構下加熱元件的材料、結構與施加電流都相等,所以靜電場分析結果相同。同理,梯度溫度場的3個仿真模型的靜電場分析結果也是相同的。
由圖4可知,施加給石墨加熱體的電流所產生的焦耳熱均勻分布在加熱體上,其值為1.462 9×107W/m3。那么在理想狀態下,燒結爐內的溫度是均勻分布的。

圖4 均勻溫度場焦耳熱分布
從圖5中可以看到,在階梯式的石墨加熱體上,三段加熱體上的焦耳熱大小明顯不同,而在各段上的焦耳熱分布基本均勻。同樣地,本次靜電場分析仿真中所得到的結果將應用于接下來的瞬態溫度場分析中。石墨加熱體上焦耳熱的明顯分區為梯度溫度場的實現提供了最基礎的理論上可靠的熱量分布狀態。
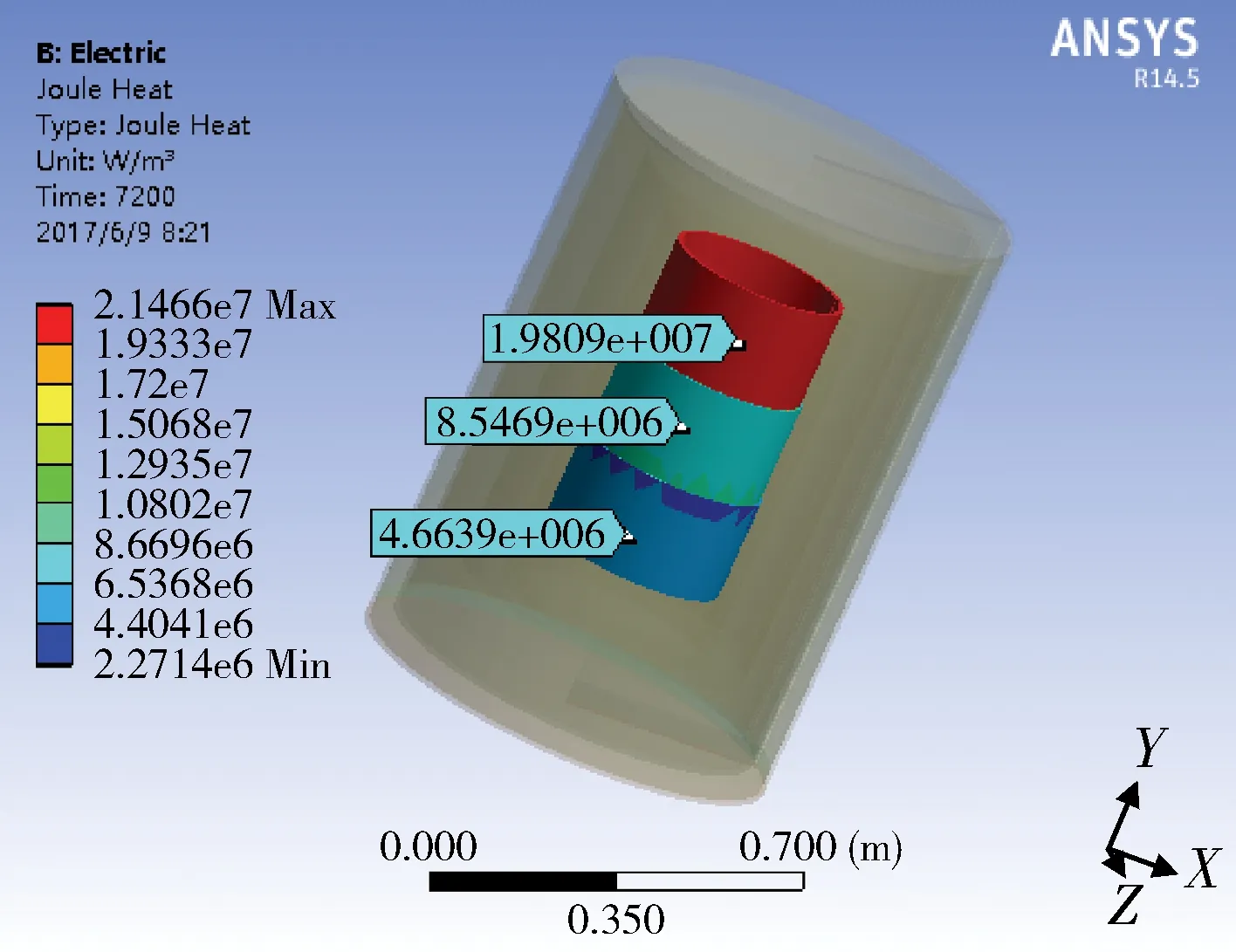
圖5 梯形溫度場焦耳熱分布
2.2 瞬態溫度場分析仿真結果
2.2.1溫度場云圖
從圖6、圖7可知,最高溫度為石墨加熱體處,由石墨加熱體向外溫度逐漸降低,直至爐殼表面溫度降為室溫。加熱體為均勻黑度,但這并不能代表加熱體上的溫度分布的均勻性,因為在溫度分布云圖中每種黑度代表了一個溫度區間,在圖6中,溫度區間大小約為263 ℃,圖7溫度區間的大小約為277 ℃,具體的溫度場均勻性分析還需從仿真模型中取出更多的溫度數值來進行分析。

圖6 結構體1溫度場云圖
其余4個仿真模型的溫度場云圖就不再一一列舉了,它們在7 200 s時的最高溫度Ta與最低溫度Ti如表3所示。

表3 7 200 s時各結構的最高溫度與最低溫度

圖7 結構體4溫度場云圖
由表3可知,在7 200 s時,各個燒結爐溫度場仿真模型的最低溫度都不超過23 ℃,與室溫接近,即爐殼的最高溫度仍然為室溫,可以說明,本設計中的6個燒結爐模型的爐襯傳熱是比較合理的,在燒結爐工作過程中爐殼溫度仍為室溫,不會過高以致于出現安全事故。
燒結爐結構一、二、四、五的爐襯厚度相同,電極石墨20 mm,碳氈層80 mm;而燒結爐結構三、六電極石墨50 mm,碳氈層厚度50 mm。通過以上數據可以看出,碳氈層的厚度對燒結爐的保溫性能有很大的影響,碳氈層越厚,燒結爐的保溫性能越好。
2.2.2升溫曲線
燒結爐中石墨加熱體的升溫曲線如圖8、圖9所示,其中圖8為均勻溫度場,圖9為梯度溫度場。
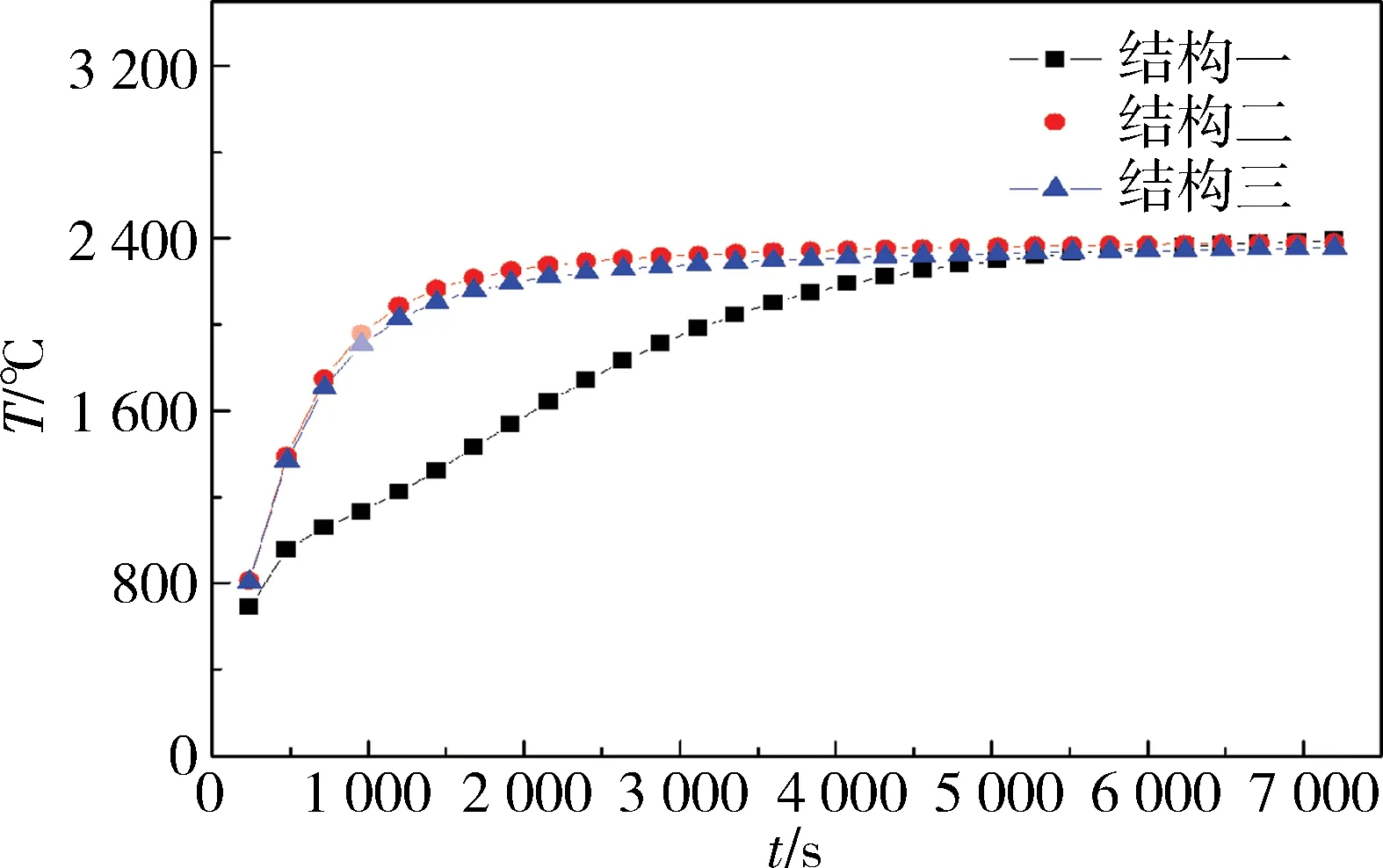
圖8 均勻溫度場升溫曲線
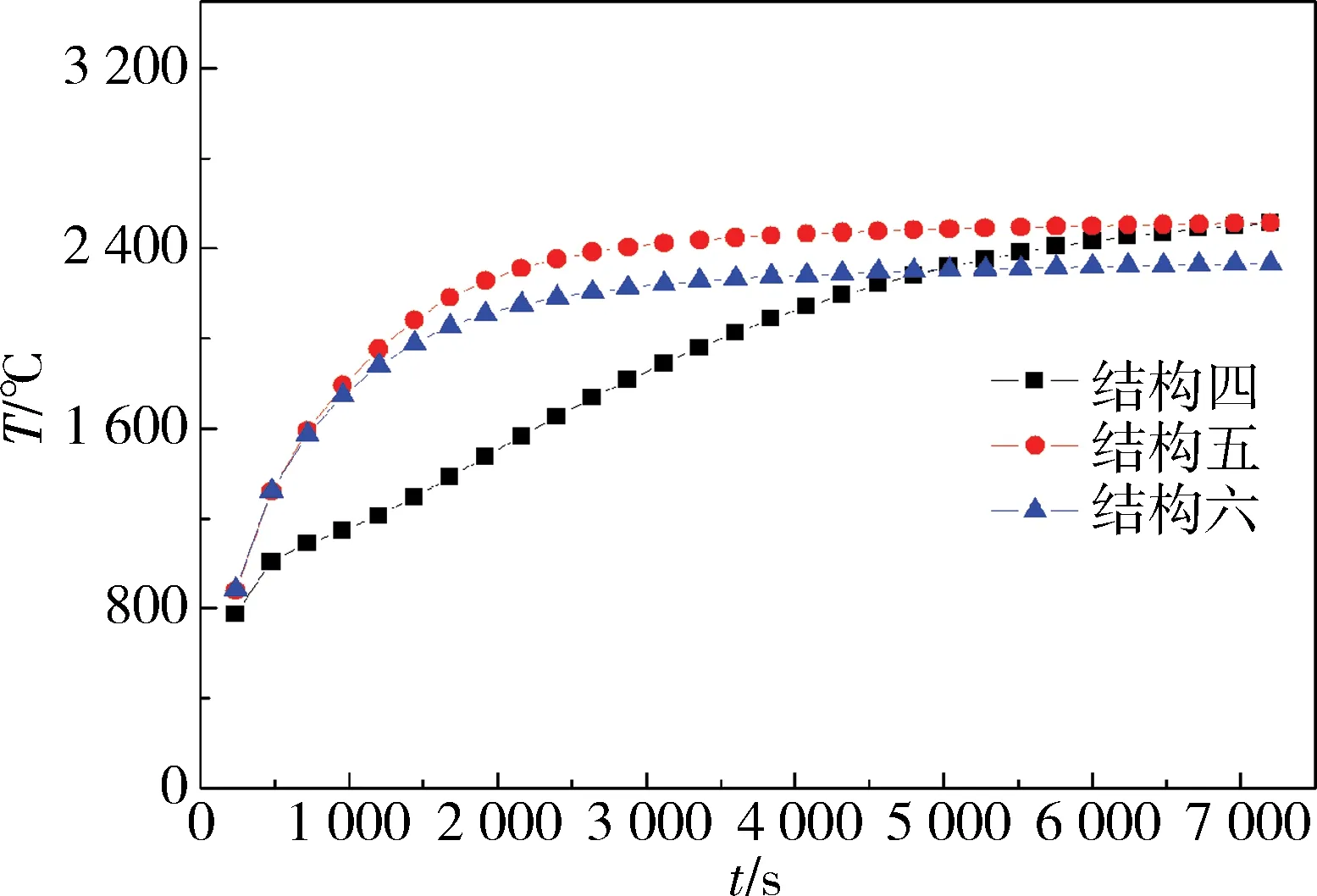
圖9 梯度溫度場升溫曲線
從圖8中可知,結構二、三在2 000 s時最高溫度已經基本穩定,而結構一在5 500 s時才接近穩定;從圖9可知,結構五、六在3 000 s時最高溫度已經基本穩定,而結構四在6 500 s時才接近穩定。
結構一與結構四的第一層隔熱層為電極石墨,而結構二、三、五、六的第一層隔熱層為硬質碳氈,其余材料均相同,通過升溫曲線可以看出電極石墨做加熱爐的隔熱層效果明顯不好,升溫速率過低。電極石墨的熱導率高達120 W·m-1·K-1,硬質碳氈的熱導率只有0.3 W·m-1·K-1,在設計加熱爐時要選擇合理的爐襯材料,熱導率過高的材料不適合作為加熱爐的隔熱層。
在均勻溫度場仿真模型中,雖然結構一的最高溫度高于結構三的最高溫度約50 ℃,但綜合考慮升溫過程,結構三的溫度場明顯優于結構一;結構二與結構三相比,它們的升溫速率基本接近,而結構二的最高溫度高于結構三的最高溫度約30 ℃,則結構二優于結構三。所以,綜合考慮最高溫度與升溫速率,在均勻溫度場的設計中,結構二為最優結構。
在梯度溫度場仿真模型中,按照分析均勻溫度場仿真模型的分析思路,綜合考慮最高溫度與升溫速率,結構五為最優,結構六次之,結構四最差。
2.2.3橫向溫度分布分析
在石墨體高600 mm情況下,以加熱底面為基準,在高300 mm處取橫截面,取4個時刻對燒結爐進行溫度分析。圖10為結構體一的溫度分布曲線,圖11為結構體二的溫度分布曲線,圖中橫坐標為距離d,表示距加熱爐模型中心軸線Y軸的距離;縱坐標為溫度T。
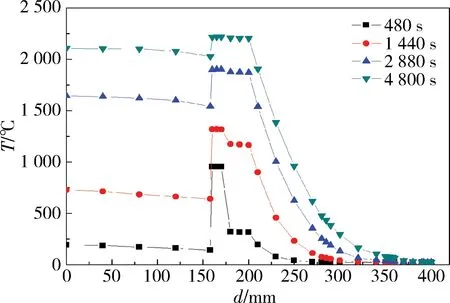
圖10 結構體一溫度曲線
燒結爐結構一與結構二僅有第一層隔熱層的材料不同,其他參數均相同,由此可以判斷,爐襯傳熱過程不同是由于第一層隔熱層材料不同所引起的,即電極石墨與硬質碳氈的不同屬性所引起的。物體的導熱能力主要由其熱導率決定,熱導率越大,導熱能力越強。由表1可知電極石墨的導熱性能遠遠強于硬質碳氈,從而導致石墨加熱體升溫速率很慢,且與電極石墨間產生較大的溫度差。其余4個結構的溫度場仿真橫向溫度分布與上述兩個仿真模型分別有著相同的規律,則不再介紹。
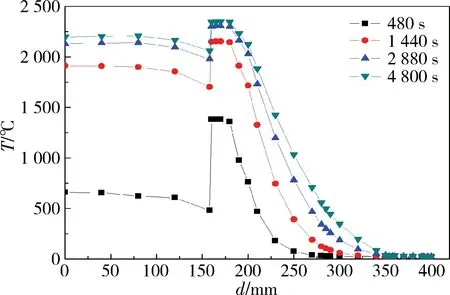
圖11 結構體二溫度曲線
2.2.4溫度梯度變化分析
為了比較均勻溫度場與非均勻溫度場的溫度梯度變化,把6種結構的溫度場仿真模型的縱向溫度擬合為直線并求出其斜率進行比較。在擬合梯度溫度場的溫度時,只對溫度呈上升趨勢的那段進行擬合。
對燒結爐縱向溫度進行擬合,分別如圖12、圖13所示。表4為6種結構的溫度梯度。
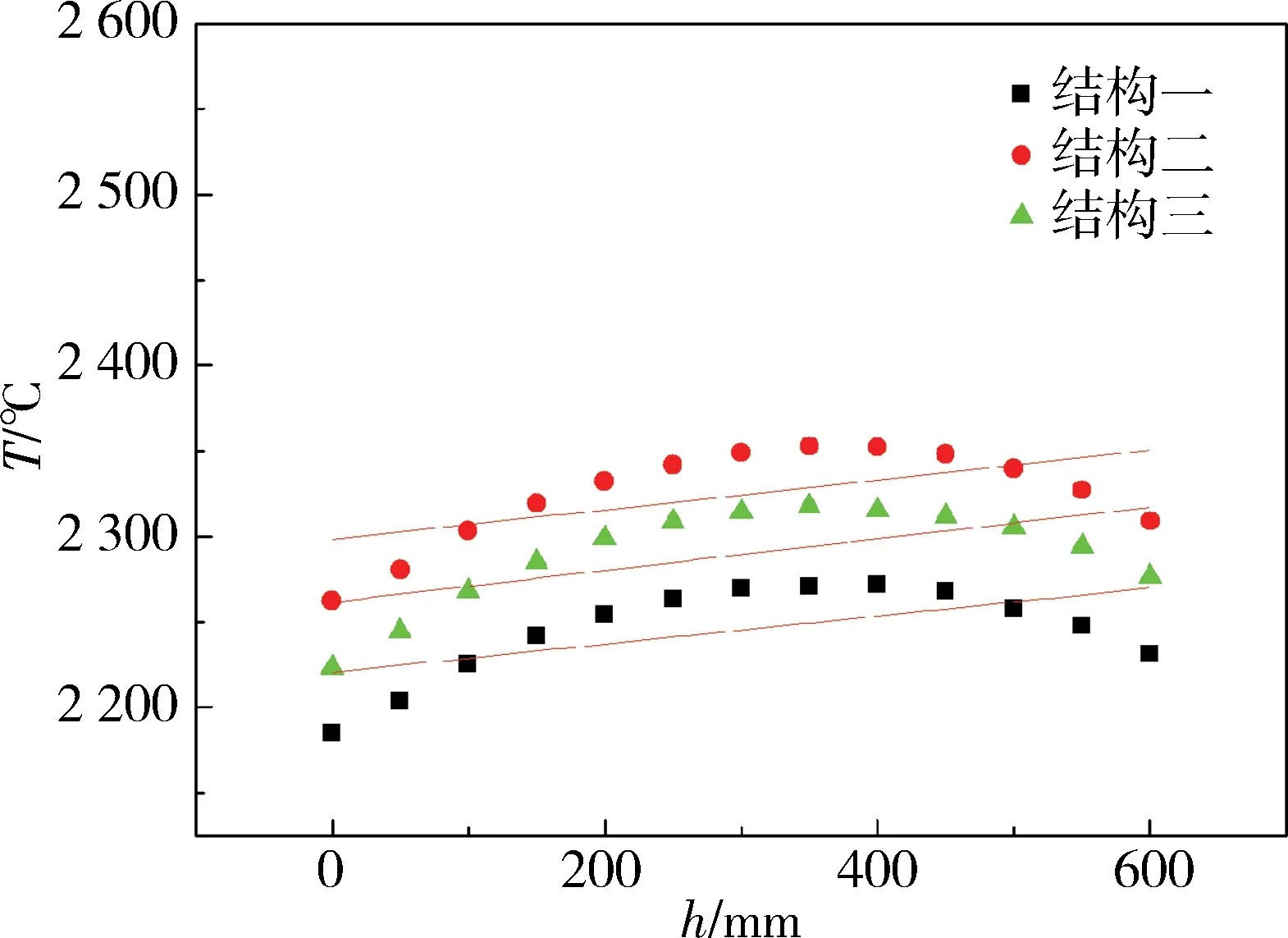
圖12 均勻溫度場縱向溫度擬合圖
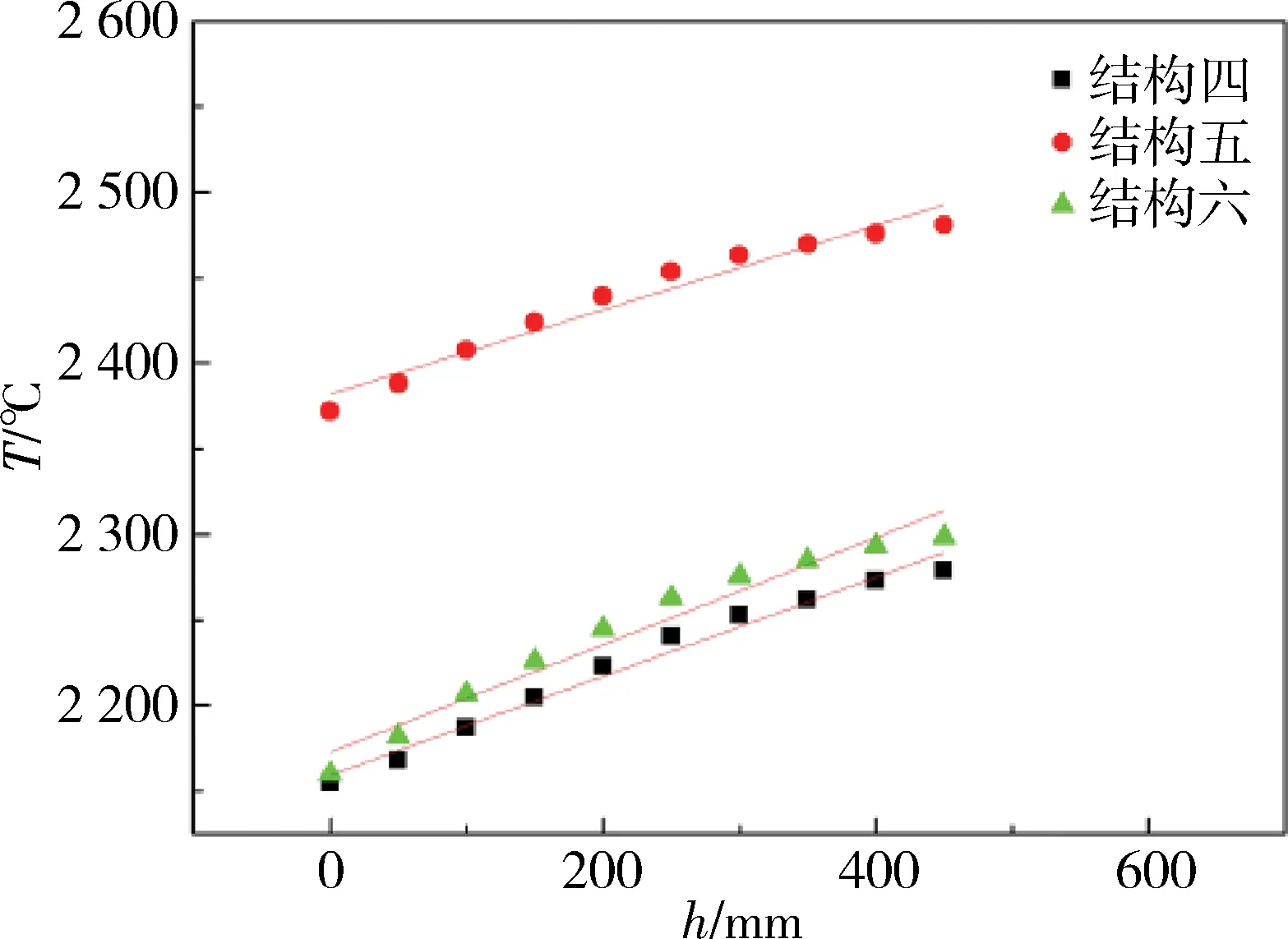
圖13 梯度溫度場縱向溫度擬合圖

結構一二三四五六ΔT/(℃/mm)0.082 10.087 570.092 590.289 350.246 330.313 61
從圖12、圖13與表4中可以清楚地看到,梯度溫度場溫度分布呈線性上升,溫度呈階梯狀分布,效果明顯,這說明了使用階梯式加熱體來實現梯度溫度場是可行的。
由表4得3個均勻溫度場燒結爐的溫度梯度比較相近,相鄰溫度梯度僅相差約0.005 ℃/mm,約為5%。綜合考慮保溫效果、升溫速率等因素,燒結爐結構二最優。
對于梯度溫度場,若實際生產或實驗研究中需要的溫度梯度較大,則斜率越大越好。由表4可知,結構六的溫度梯度最大,結構四次之,結構五最差。
3 結論
(1)通過靜電場分析,當輸入功率一定時,圓筒式加熱體的焦耳熱均勻分布,其值為定值;而階梯式加熱體的焦耳熱分布呈階梯式分布。
(2)硬質碳氈層的厚度越大、碳氈層的厚度越小,溫度場溫度梯度越大,但保溫效果有所下降。在設計梯度溫度燒結爐時,可根據所需要的溫度梯度大小來設計爐襯厚度。
(3)加熱體的形狀、爐襯結構直接影響燒結爐內溫度場的動態分布。

