家用燃?xì)庠顭峁ば阅軠y(cè)量及不確定度評(píng)定*

胡偉健，李志宏

0 引言

家用燃?xì)庠钭鳛槲覈?guó)家庭中普及率最高的一種廚房加熱器具，其熱工性能（熱負(fù)荷和熱效率）越來(lái)越受到消費(fèi)者的重視。2008年5月1日開始實(shí)施的GB16410-2007要求嵌入式灶熱效率大于等于50%，臺(tái)式灶大于等于55%，同時(shí)規(guī)定，熱負(fù)荷偏差應(yīng)該在±10%以內(nèi)。而最新版本的GB16410—201X《家用燃?xì)庠罹摺罚ㄕ髑笠庖姼澹﹦t要求嵌入式灶熱效率大于等于55%，臺(tái)式灶大于等于58%，同時(shí)規(guī)定，熱負(fù)荷偏差應(yīng)該在±10%以內(nèi)。

2012年12月3日，國(guó)家質(zhì)量監(jiān)督檢驗(yàn)檢疫總局發(fā)布《測(cè)量不確定度評(píng)定與表示》（GUM法）（JJF1059.1-2012）代替JJF1059-1999。2012年12月21日發(fā)布《用蒙特卡洛法評(píng)定測(cè)量不確定度》（JJF1059.2-2012），將蒙特卡洛法作為對(duì)GUM法的重要補(bǔ)充。根據(jù)我國(guó)《測(cè)量不確定度政策》的規(guī)定，檢測(cè)實(shí)驗(yàn)室應(yīng)有能力對(duì)每一項(xiàng)有數(shù)值要求的測(cè)量結(jié)果進(jìn)行測(cè)量不確定度評(píng)定。當(dāng)不確定度與檢測(cè)結(jié)果的有效性或應(yīng)用有關(guān)、當(dāng)測(cè)試方法中有規(guī)定時(shí)和認(rèn)可委員會(huì)有要求時(shí)，檢測(cè)報(bào)告必須提供測(cè)量結(jié)果的不確定度[1]。

熱負(fù)荷和熱效率作為家用燃?xì)庠顭嵝阅艿闹匾笜?biāo)，有必要對(duì)其測(cè)量結(jié)果進(jìn)行不確定度評(píng)定。由于其測(cè)量模型比較復(fù)雜，且為非線性，采用GUM法評(píng)定不確定度，所求偏導(dǎo)比較困難，于是基于蒙特卡洛法的不確定度評(píng)定是有效的代替方法。

1 用蒙特卡洛法評(píng)定測(cè)量不確定度

1.1 蒙特卡洛法簡(jiǎn)介

蒙特卡洛法主要是用相關(guān)函數(shù)產(chǎn)生服從相應(yīng)概率分布的隨機(jī)數(shù)對(duì)各個(gè)輸入量進(jìn)行多次隨機(jī)抽樣，然后再進(jìn)行概率分布傳播，最后得到輸出量的模擬結(jié)果，所以只要試驗(yàn)次數(shù)足夠大，最后的模擬結(jié)果便近似于事件發(fā)生的概率，便可估計(jì)輸出量的有關(guān)特征量。近年來(lái)，該方法被廣泛的應(yīng)用于測(cè)量不確定度的評(píng)定，其核心是求取模擬樣本的標(biāo)準(zhǔn)差。其依據(jù)是分布傳播，即能夠通過(guò)輸入量的概率分布確定輸出量的概率分布。圖1是概率分布傳遞的示意圖。求解步驟按照用蒙特卡洛法評(píng)定測(cè)量不確定度[2-4]。

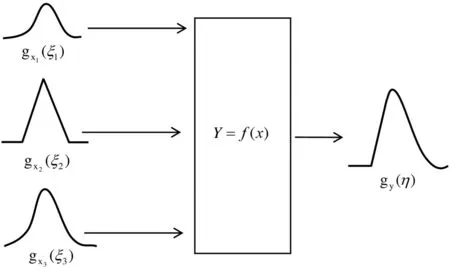
圖1 3個(gè)獨(dú)立的輸入量的概率分布傳遞示意圖Fig.1 Illustration of propagation of probability distributions for 3 independent input quantities

1.2 家用燃?xì)庠顭嶝?fù)荷測(cè)量不確定度評(píng)定示例

（1）測(cè)量原理和測(cè)量模型

熱負(fù)荷是指低熱值與燃?xì)饬髁康某朔e。本次試驗(yàn)選用某燃?xì)庠钅苄Ъ熬C合性能測(cè)試臺(tái)對(duì)三種不同品牌的三個(gè)家用燃?xì)庠睿?2T）的左爐（分別標(biāo)記為1、2、3號(hào)灶）進(jìn)行熱負(fù)荷對(duì)比測(cè)試。如圖2所示，將燃?xì)庠钆c測(cè)試平臺(tái)連接。燃?xì)馔ㄟ^(guò)閥門流經(jīng)濕式氣體流量計(jì)，最后到燃?xì)庠睢Ｆ渲袧袷綒怏w流量計(jì)的燃?xì)饬髁俊⑷細(xì)鉁囟取⑷細(xì)忪o壓力以及大氣壓力等參數(shù)是通過(guò)測(cè)試平臺(tái)的傳感器采集，并進(jìn)行自動(dòng)計(jì)算，最后將結(jié)果呈現(xiàn)在測(cè)試平臺(tái)的屏幕上的。測(cè)試按照GB30720—2014《家用燃?xì)庠罹吣苄薅ㄖ导澳苄У燃?jí)》[5]中的步驟進(jìn)行。

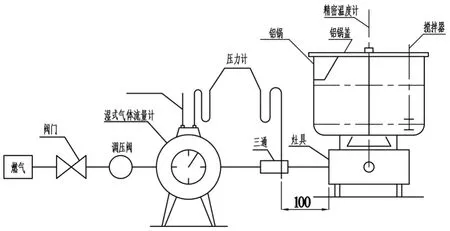
圖2 熱負(fù)荷測(cè)量原理示意圖Fig.2 Heat load measuring principlediagram

實(shí)測(cè)熱負(fù)荷用公式（1）計(jì)算：

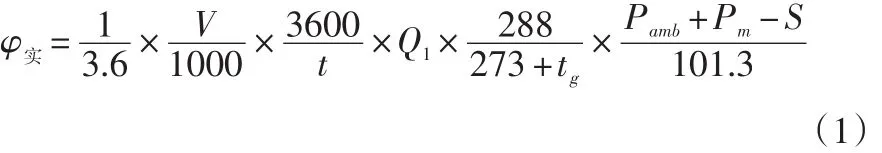
φ實(shí)—實(shí)測(cè)熱負(fù)荷，單位為千瓦(kW)；

Q1—15℃、101.3 kPa狀態(tài)下試驗(yàn)燃?xì)獾牡蜔嶂担瑔挝粸檎捉苟苛⒎矫?MJ/m3)；

V—測(cè)試耗氣量，單位為L(zhǎng)；

tg—燃?xì)饬髁坑?jì)內(nèi)的燃?xì)鉁囟龋瑔挝粸閿z氏度(℃)；

Pamb—試驗(yàn)時(shí)的大氣壓力，單位為千帕(kPa)；

Pm——實(shí)測(cè)燃?xì)饬髁坑?jì)內(nèi)的燃?xì)庀鄬?duì)靜壓力，單位為千帕(kPa)；

S——溫度為tg時(shí)的飽和水蒸氣壓力，單位為千帕(kPa)(當(dāng)使用干式流量計(jì)測(cè)量時(shí)，S值應(yīng)乘以試驗(yàn)燃?xì)獾南鄬?duì)濕度進(jìn)行修正)；

t——試驗(yàn)時(shí)間，單位秒（s）。

（2）測(cè)量數(shù)據(jù)

對(duì)三個(gè)家用燃?xì)庠畹母鱾€(gè)輸入量分別進(jìn)行10次獨(dú)立測(cè)量，計(jì)算得到輸入量的試驗(yàn)標(biāo)準(zhǔn)差如表1。

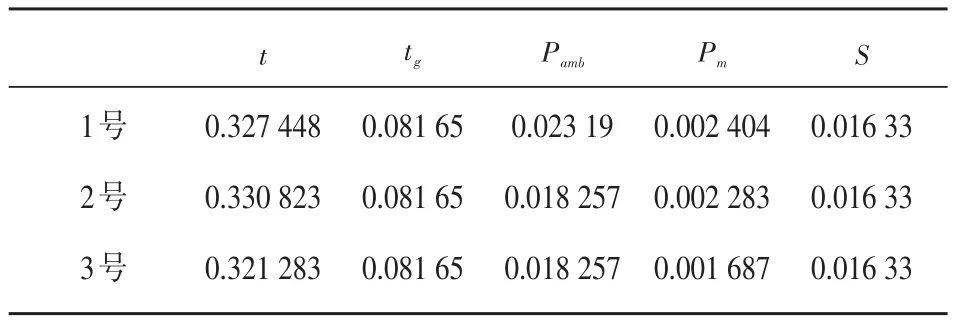
表1 1、2、3號(hào)灶熱負(fù)荷各輸入量結(jié)果數(shù)據(jù)表Table1 Datasheet of heat input for 1，2 and 3 stoves

其中耗氣量V為10，是一個(gè)固定值，這樣只要記錄對(duì)應(yīng)時(shí)間就可以求得燃?xì)饬髁俊Ｌ烊粴獾牡蜔嶂礠1根據(jù)GBT11062-2014中低熱值體積發(fā)熱量的計(jì)算方法計(jì)算，本次試驗(yàn)所用天然氣成分為甲烷含量≥99%，乙烷含量≤0.6%，空氣含量≤0.4%，具體計(jì)算過(guò)程如下：

已知組成混合物，在燃燒溫度t1，計(jì)量溫度t2和壓力p2時(shí)的理想氣體體積發(fā)熱量用公式（2）

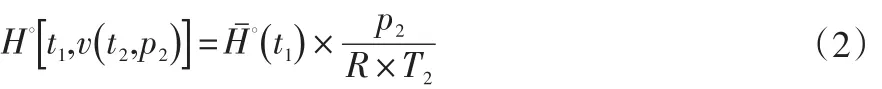
式 Hˉ°(t1)為混合物的理想摩爾發(fā)熱量可查GB/T 11062-2014表3獲得； R為摩爾氣體常數(shù)（8.31451 J.mol-1.K-1）；T2為絕對(duì)溫度（T2=t1+273.15）。

當(dāng)乙烷含量為0.6%，空氣含量為0，甲烷含量為99.4%時(shí)低熱值取上限

當(dāng)乙烷含量為0，空氣含量為0.4%，甲烷含量為99.6%時(shí)低熱值取下限，

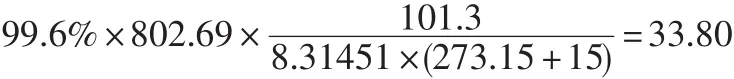
因此天然氣低熱值的取值范圍為[33.80，34.10]，根據(jù)最大熵原理[6-7]，天然氣低熱值為均勻分布，因此可以取值其最大允許誤差為±0.15，則其標(biāo)準(zhǔn)不確定度為

（3）A類測(cè)量不確定度評(píng)定

將前兩次測(cè)量值的均值作為測(cè)量結(jié)果時(shí)，則A類測(cè)量不確定度為u(x)=。結(jié)果如表2所示。

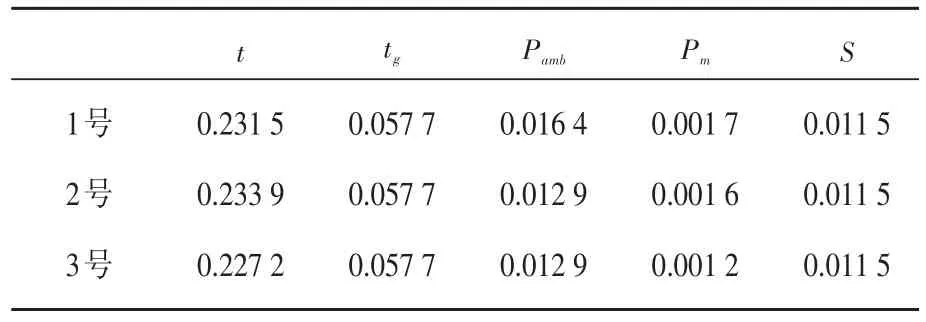
表2 1、2、3號(hào)灶熱負(fù)荷各輸入量的標(biāo)準(zhǔn)不確定度Table2 Standard uncertainty of heat input for 1，2 and 3 stoves

（4）分布傳遞的結(jié)果

由最大熵原理可以求得各個(gè)輸入量均為正態(tài)分布。當(dāng)把前兩次測(cè)量值的均值作為測(cè)量結(jié)果時(shí)，采用蒙特卡洛法傳遞概率分布[8-11]，利用MATLAB軟件進(jìn)行計(jì)算。1、2、3號(hào)灶的運(yùn)行結(jié)果如表3所示，輸出量Y也即實(shí)測(cè)熱負(fù)荷的概率分布如圖3所示。取三個(gè)灶擴(kuò)展不確定度的平均值作為本套設(shè)備熱負(fù)荷測(cè)量不確定度的最終值，即為0.76%。

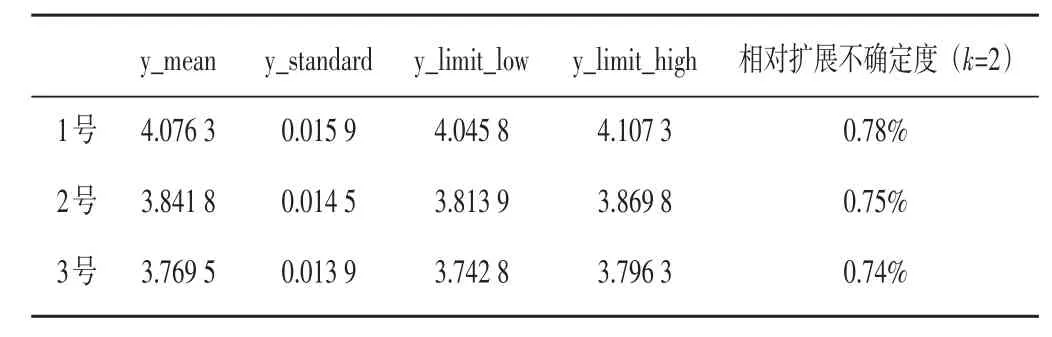
表3 1、2、3號(hào)灶熱負(fù)荷的不確定度Table3 Uncertainty of heat load for 1，2 and 3 stoves

1.3 家用燃?xì)庠顭嵝蕼y(cè)量不確定度評(píng)定示例

（1）測(cè)量原理和測(cè)量模型

熱效率是指系統(tǒng)有效輸出的能量與輸入的能量之比。同理對(duì)三個(gè)燃?xì)庠钸M(jìn)行熱效率試驗(yàn)，測(cè)試步驟按照GB30720-2014《家用燃?xì)庠罹吣苄薅ㄖ导澳苄У燃?jí)》中熱效率試驗(yàn)方法進(jìn)行。由式（3）計(jì)算實(shí)測(cè)熱效率。

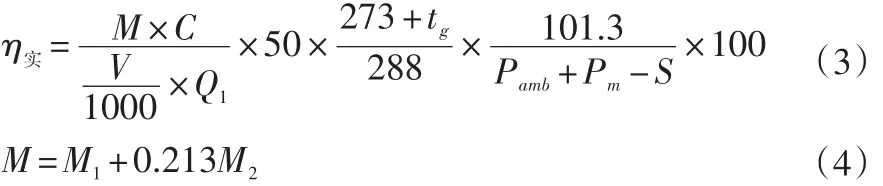
M——實(shí)際加水量與鋁鍋換算為當(dāng)量加水量之和，單位為千克（kg）；

M1——加入鍋內(nèi)的水質(zhì)量，單位為千克（kg）；

M2——鋁鍋的質(zhì)量（含蓋子和攪拌器），單位為千克（kg）；

試驗(yàn)完上限鍋和下限鍋的實(shí)測(cè)熱效率后用式（5）計(jì)算總熱效率。

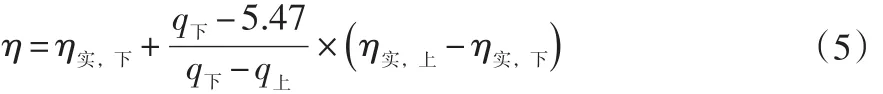
η——灶頭總熱效率，%；

η實(shí)，下——使用下限鍋時(shí)的實(shí)測(cè)熱效率，%；

η實(shí)，上——使用上限鍋時(shí)的實(shí)測(cè)熱效率，%；

q下——使用下限鍋試驗(yàn)時(shí)的鍋底熱強(qiáng)度，單位為瓦每平方厘米（W/cm2）；

q上——使用上限鍋試驗(yàn)時(shí)的鍋底熱強(qiáng)度，單位為瓦每平方厘米（W/cm2）；

注：鍋底熱強(qiáng)度等于實(shí)測(cè)熱負(fù)荷（W）/試驗(yàn)用鍋在正投影面的面積（cm2）。

根據(jù)式（5），熱效率η的輸入量有實(shí)測(cè)熱效率η實(shí)和鍋底熱強(qiáng)度q，而實(shí)測(cè)熱負(fù)荷又是鍋底熱強(qiáng)度q的輸入量。因此，可以分別評(píng)定實(shí)測(cè)熱效率和實(shí)測(cè)熱負(fù)荷的不確定度，以其作為輸入量，再評(píng)定燃燒器熱效率的測(cè)量不確定度，則式（5）就可以作為燃燒器熱效率的數(shù)學(xué)模型。

圖3 1、2、3號(hào)灶熱負(fù)荷概率分布圖Fig.3 Probability distribution of heat load for 1，2 and 3 stoves

（2）測(cè)量數(shù)據(jù)

同理對(duì)三臺(tái)灶的各個(gè)輸入量進(jìn)行10次獨(dú)立測(cè)量，計(jì)算得到輸入量的試驗(yàn)標(biāo)準(zhǔn)差如表4和表5所示。

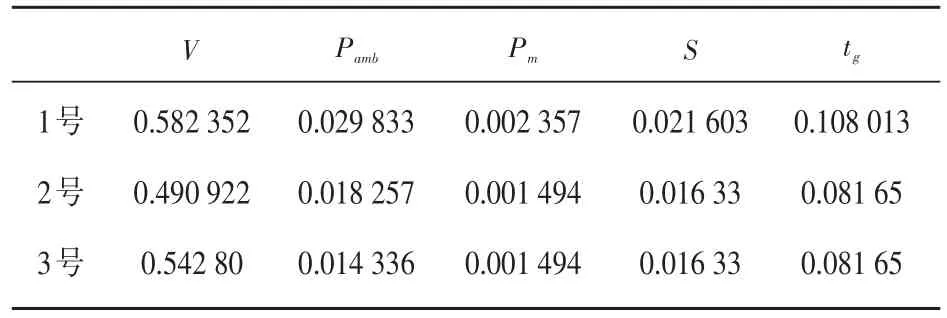
表4 三個(gè)灶的下限鍋熱效率各輸入量數(shù)據(jù)Table4 Theinput dataof thermal efficiency of lower limit

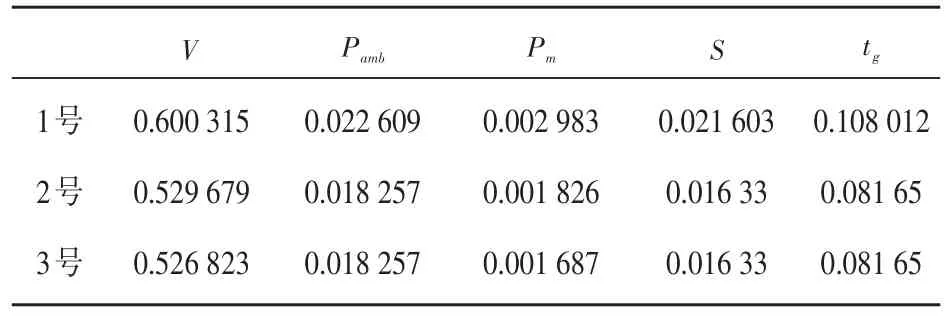
表5 三個(gè)灶的上限鍋熱效率各輸入量數(shù)據(jù)Table5 Theinput dataof thermal efficiency of upper limit

（3）A類不確定度評(píng)定

同理將前兩次測(cè)量值的平均值作為測(cè)量結(jié)果，可以得出三個(gè)灶的下限鍋和上限鍋熱效率各輸入量的標(biāo)準(zhǔn)不確定度。結(jié)果如表6和表7所示。

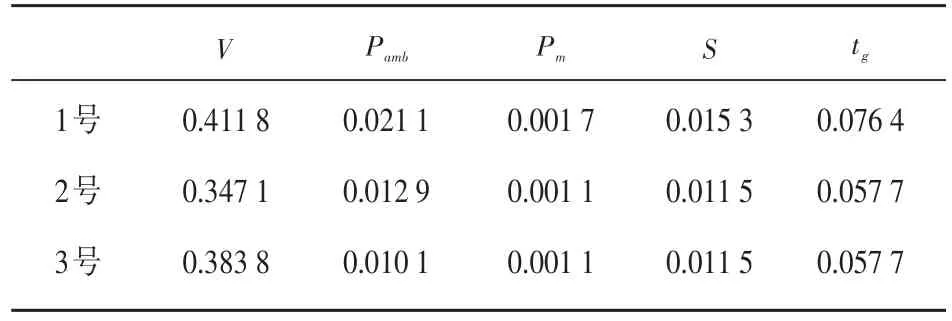
表6 下限鍋熱效率各輸入量的標(biāo)準(zhǔn)不確定度Table 6 The standard uncertainty of each input quantity of lower pot thermal efficiency

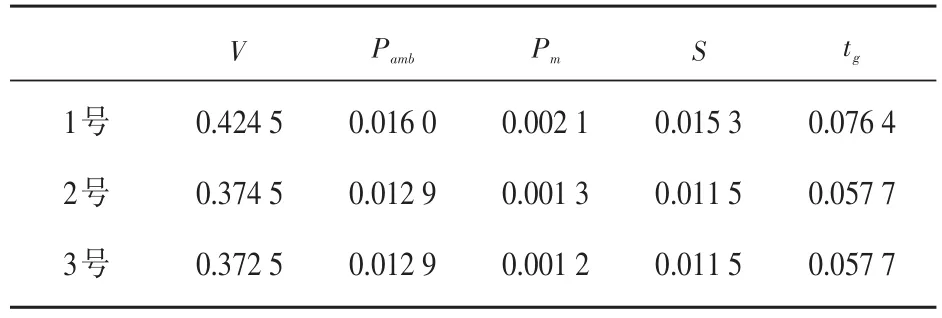
表7 上限鍋熱效率各輸入量的標(biāo)準(zhǔn)不確定度Table 7 The standard uncertainty of each input quantity of theupper pot heat efficiency

（4）分布傳遞結(jié)果

將兩次測(cè)量值的平均值作為測(cè)量結(jié)果，采用蒙特卡洛法傳遞概率分布，利用MATLAB軟件進(jìn)行計(jì)算，則三個(gè)灶的總的實(shí)測(cè)熱效率的概率分布如圖4所示，總熱效率的計(jì)算結(jié)果如表8所示。

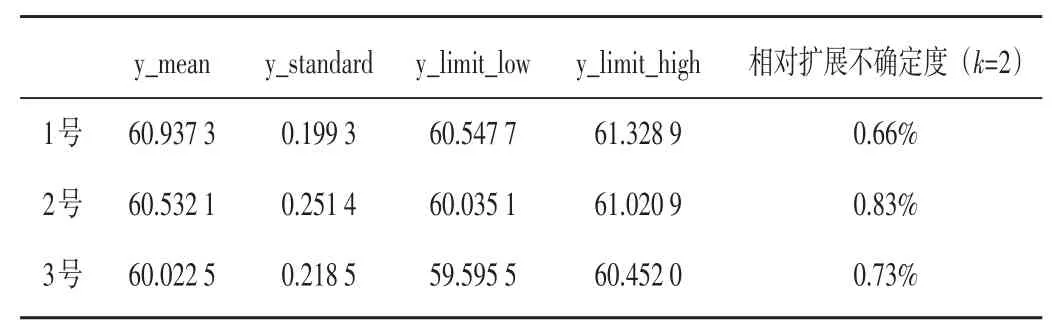
表8 三個(gè)灶兩次測(cè)量的熱效率的不確定度Table8 Uncertainty in thermal efficiency of threefocifor twomeasurements

2 用GUM法評(píng)定測(cè)量不確定度

2.1 1號(hào)灶實(shí)測(cè)熱負(fù)荷的GUM法評(píng)定

根據(jù)實(shí)測(cè)熱負(fù)荷的模型和不確定度傳遞率，取兩次測(cè)量的平均值作為測(cè)量結(jié)果時(shí)，合成標(biāo)準(zhǔn)不確定度的公式如式（6）所示。

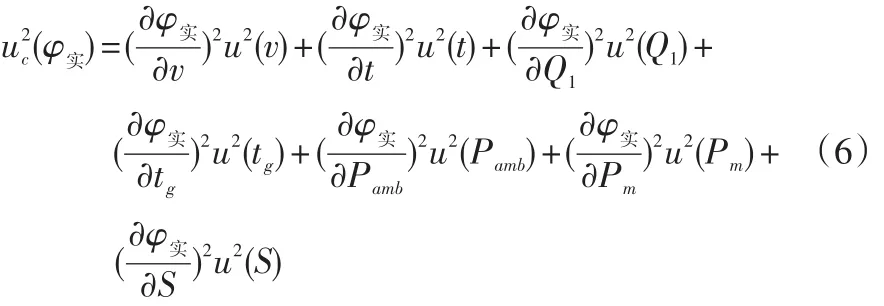
圖4 三個(gè)灶總實(shí)測(cè)熱效率概率分布圖Fig.4 Probability distribution of total measured thermal efficiency of threestoves

其中，

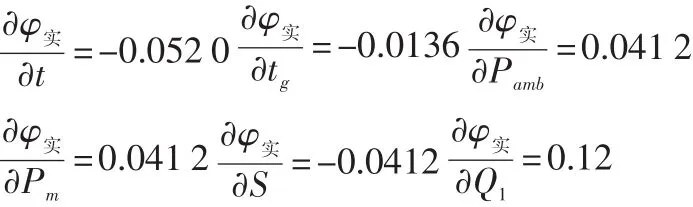
將數(shù)據(jù)代入式（6）得：

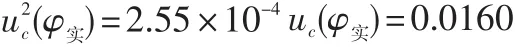
2.2 1號(hào)灶實(shí)測(cè)熱效率的GUM法評(píng)定

根據(jù)實(shí)測(cè)熱效率的模型和不確定度傳遞率，取兩次測(cè)量的平均值作為測(cè)量結(jié)果時(shí)，上限鍋合成標(biāo)準(zhǔn)不確定度的公式如式（7）所示：

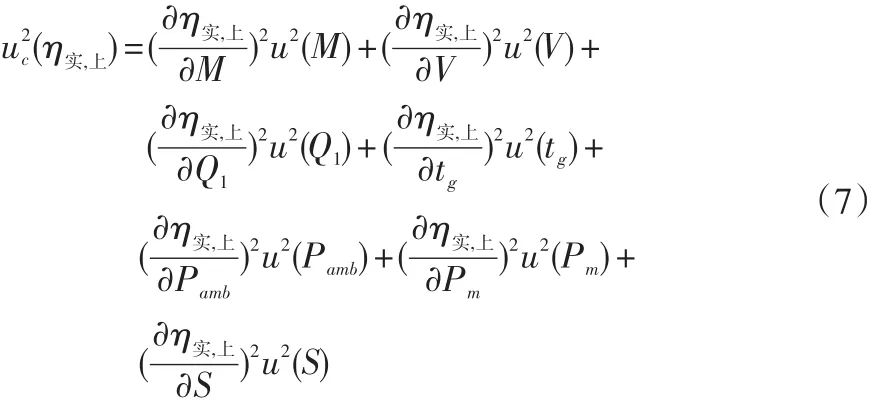
其中，

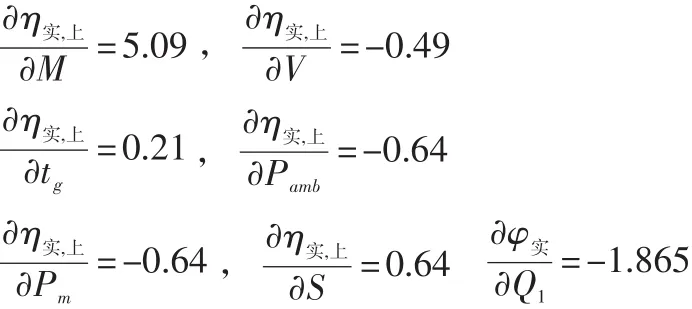
代入式（7）得 uc(η實(shí),上)=0.2653。

同理，下限鍋實(shí)測(cè)熱效率的合成標(biāo)準(zhǔn)不確定度公式為：

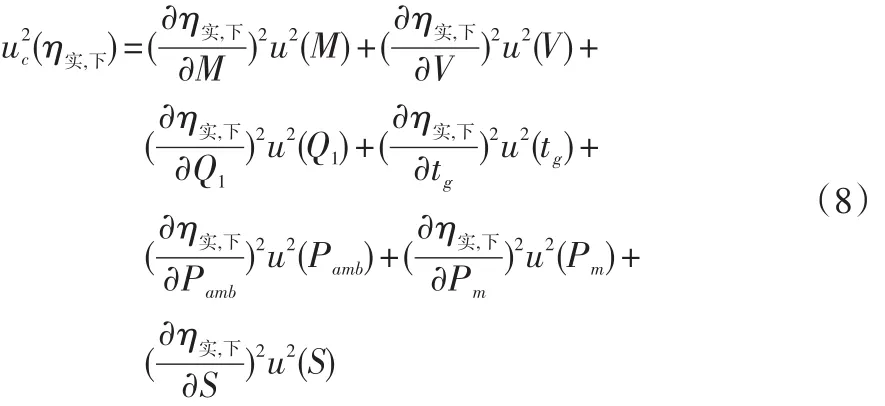
其中，

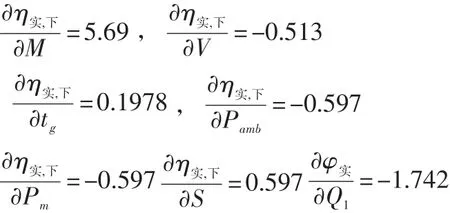
代入式 （8） 得 uc(η實(shí),下)=0.261 0 。

于是，總的熱效率的合成標(biāo)準(zhǔn)不確定度公式為：

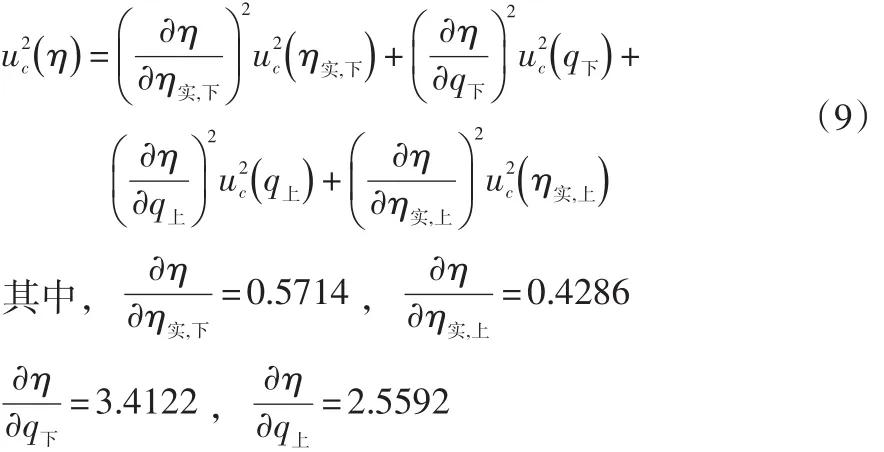
代入式（9）得uc(η)=0.1996，則其相對(duì)擴(kuò)展不確定度為×100%×2=0.66%，同理可以求得其他兩個(gè)灶的相對(duì)擴(kuò)展不確定度分別為0.83%、0.73%。

3 MCM和GUM的比較

綜上所述，熱負(fù)荷MCM和GUM計(jì)算的結(jié)果如表9所示；熱效率MCM和GUM計(jì)算的結(jié)果如表10所示。可以看出兩者結(jié)果是一致的。

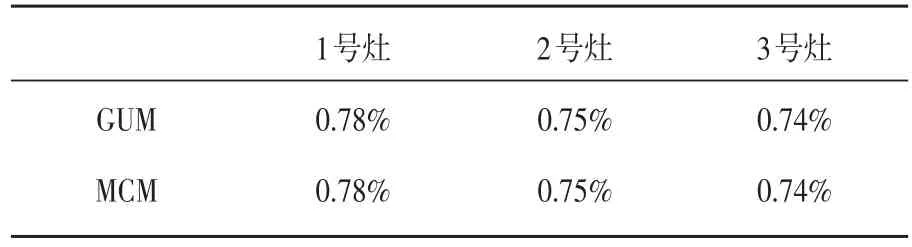
表9 三個(gè)灶熱負(fù)荷MCM和GUM結(jié)果統(tǒng)計(jì)表Table9 Threeheat load MCMand GUMstatistical tables

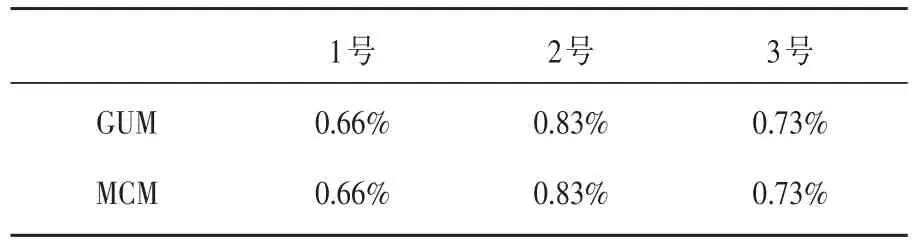
表10 三個(gè)灶的總熱效率MCM和GUM結(jié)果統(tǒng)計(jì)表Table 10 The total thermal efficiency of three foci MCM and GUM resultstable

4 結(jié)論

用蒙特卡洛法進(jìn)行概率分布傳遞，最后實(shí)測(cè)熱負(fù)荷和總熱效率的模擬結(jié)果為正態(tài)分布。

用GUM法和MCM法兩種方法評(píng)定的熱負(fù)荷和熱效率的不確定度結(jié)果一致。

在GUM法的評(píng)定過(guò)程中可知試驗(yàn)時(shí)間的測(cè)量不確定度對(duì)熱負(fù)荷測(cè)量結(jié)果不確定度的影響最大；當(dāng)量加水量的測(cè)量不確定度對(duì)熱效率測(cè)量結(jié)果不確定度的影響最大。

將三個(gè)灶用MCM法評(píng)定熱負(fù)荷的不確定度的平均值作為本套設(shè)備的最終不確定度，結(jié)果為0.76%，熱效率的最終不確定度為0.74%。