基于用戶利益與出行意愿的電動汽車充放電調度策略*

楊春萍，趙祺，祁兵，李彬，崔高穎

(1．華北電力大學電氣與電子工程學院，北京102206;2．國網江蘇省電力公司電力科學研究院，南京210003)

0 引言

文獻［1］構建了用戶選擇充電時間對峰谷電價時段的響應模型;通過蒙特卡洛法模擬得到電動汽車充電負荷的日負荷曲線，并與原始電網負荷曲線疊加，從而形成實施效果下的電網實際負荷情況。在此基礎上建立了以峰谷差率最小為目標的最優化模型，通過遺傳算法對峰谷電價時段優化問題進行了求解。文獻［2］利用蒙特卡洛法對大規模電動汽車接入電網充電負荷進行評估的基礎上，建立了電動汽車有序充電模型。以電網負荷削峰填谷為目標，通過遺傳算法建立針對電動汽車負荷的需求側響應策略優化模型。文獻［3］仿真了四種情境下電動汽車充電對電網的影響，得到在非電網運營機構會采取分批充電的模式下可以讓電動汽車電池的充電功率比較均勻地分布在谷期階段，有效地填充了負荷低谷。文獻［4］提出有序充電的智能控制策略，采用中間管理者，將集中優化控制與分布式優化控制相結合。文獻［5］提出考慮電動汽車充電站布局優化的配網規劃模型，提出了一種新的輻射狀約束保證可行解對應的規劃方案均為輻射狀網絡。文獻［6］提出了一種含電動汽車的新型直流配電網，提高分布式發電的利用率，并節省儲能裝置的投資。文獻［7］為電動汽車用戶設計了一種充放電策略，使用戶在保證正常需求的情況下可以在低電價時段充電，高電價時段向電網售電。文獻［8］對充換電和集中充電統一配送這兩種換電模式的結構、運營流程進行了分析，提出分別以總充電費用最小和日負荷曲線波動最小為目標兩階段有序充電優化模型。文獻［9］提出了電動汽車充電分時電價時段劃分方法，并建立了以用戶充電費用最小和電池起始充電時間最早為控制目標的數學模型。文獻［10］利用分時電價機制引導和蒙特卡洛方法模擬不同管理模式下的EV負荷，采用場景生成和K均值聚類算法構造風光典型場景集，以年總經濟成本最優為目標函數，經粒子群算法優化得出含EV的微電網容量配置方案。文獻［11］重點介紹了V2G技術中電動汽車與電網互動雙向電能檢測系統的設計，并對雙向電能檢測系統進行軟硬件的設計。

1 問題的描述

由于電動汽車隸屬于用戶的私人財產，用戶的使用意愿具有隨意性、不可控性，如果在調控過程中使用戶的利益受損，電網將會失去與用戶合作的機會。因此，電動汽車的充放電調度需要建立在用戶滿意度的前提下。本文首先考慮用戶的利益與出行意愿，其次考慮電動汽車放電對電網的削峰影響。

1．1 目標函數的建立

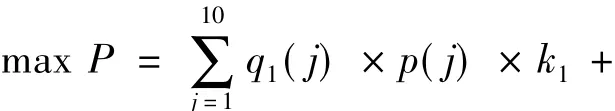
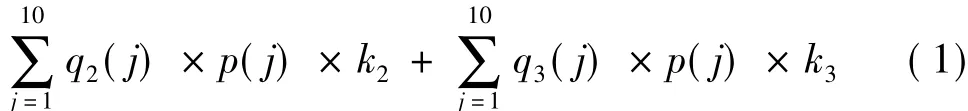
式中P為30輛電動汽車在10個時刻內的總收益;q1(j)為在j時刻正在充電電動汽車的數量;q2(j)為在j時刻不充電也不放電電動汽車的數量;q3(j)為在j時刻正在放電的電動汽車的數量，其中q1(j)+q2(j)+q3(j)=30;k1為－1，代表電動汽車正在充電;k2為1，代表電動汽車正在放電;k3為0，代表電動汽車既不充電也不放電。

1．2 約束條件

(1)單個用戶收益約束

P(i)≥0 (2)

為保障每個用戶的利益，應當設置單個用戶收益約束，使每個用戶收益都處于不虧損狀態，如若調控結束后P(i)＜0，則應給予用戶響應補貼，直至P(i)=0。

(2)放電上限約束與充電下限約束

10%≤SOC(i)≤90% (3)

不管調控策略是否對電動汽車i進行放電，當SOC(i)≥90%時，都對電動汽車i進行放電操作。當電動汽車SOC(i)≤10%時，電動汽車電量不足，不管調控策略對電動汽車i如何調控，此時對電動汽車i進行充電操作。

(3)峰谷差值約束

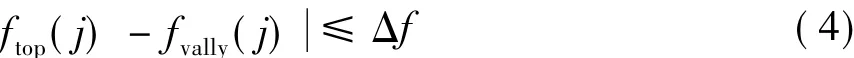
式中ftop為j時刻之前的峰時負荷值;fvally為j時刻之前的谷時負荷值;Δf為峰谷差值上限，當峰谷差值低于此上限時，對剩余電量不足10%的電動汽車進行充電操作;當峰谷差值高于此上限時，按照粒子群算法對電動汽車進行充放電操作。

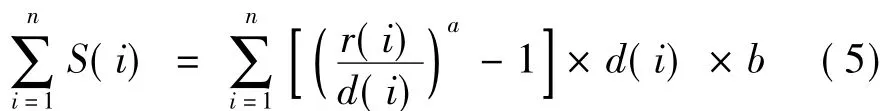
(4)滿意度約束0≤S(i)≤Stop(6)在第二階段調度中，當S(i)＞0時，用戶處于滿意狀態，滿意度值S(i)的增加速度會隨著實際電量值增加而減慢;即當電動汽車電量滿足用戶所需電量時，用戶會感到滿意，但是在電動汽車電量滿足用戶所需電量的前提下，隨著充電的進行，用戶的滿意度的增加速度遠小于實際電量值的增加速度;這時為了給用戶節約電費，應當設置滿意度上限值Stop。

2 模型的建立

考慮用戶的利益，建立基于粒子群算法的第一階段模型與基于用戶滿意度的第二階段模型。選取日間12個時刻對電動汽車進行充放電調控，設置前10個時刻為第一階段，在第一階段中首先利用粒子群算法確定各個時刻充電電動汽車與放電電動汽車的數量，再根據各個電動汽車的剩余電量與相應的約束條件，對具體哪幾輛電動汽車充電，哪幾輛電動汽車放電進行調控，目的在于在整個調控過程中使用戶的利益得到最佳化;設置后兩個時刻為第二階段，在第二階段中，根據第一階段末尾電動汽車剩余電量與用戶設置行程所需電量計算得出用戶滿意度值，繼而根據滿意度值對電動汽車進行調控，目的在于在整個調控過程結束后，在保障用戶利益的基礎上，使剩余電量能夠滿足用戶的需求，如圖1所示。

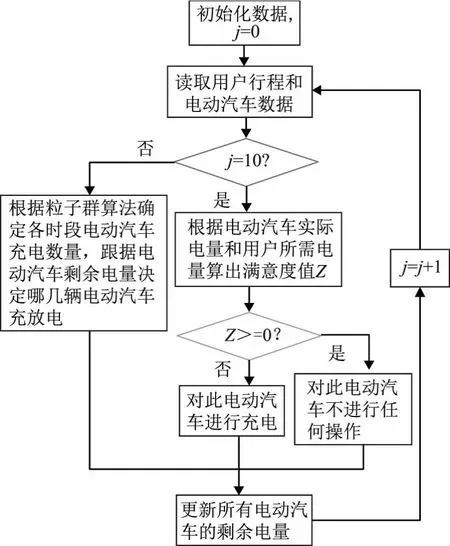
圖1 電動汽車調控模型Fig．1 Electric vehicle control model

2．1 第一階段模型

在第一階段模型中，利用粒子群算法對充放電電動汽車數量確定下來;再根據電動汽車電量對具體電動汽車進行充放電操作;使用戶的利益得到最佳化，并保障電動汽車電池不會過度放電。

2．1．1 粒子群算法

在粒子群算法中，對一群沒有質量和體積的粒子進行初始化，每個粒子都是目標問題的潛在解向量，根據適用度函數算出每個粒子的適應值，再通過與個體極值、種群極值對比，逐漸向最優值靠攏，其中粒子利用式(7)更新速度，利用式(8)更新位置，經過若干次的迭代，得到最優解向量。圖2為粒子群算法流程圖。

V(i)=w×V(i)+c1×rand()×［pbest(i)－present(i)］+c2×rand()×［gbest(i)－present(i)］ (7)

present(i)=present(i)+V(i) (8)

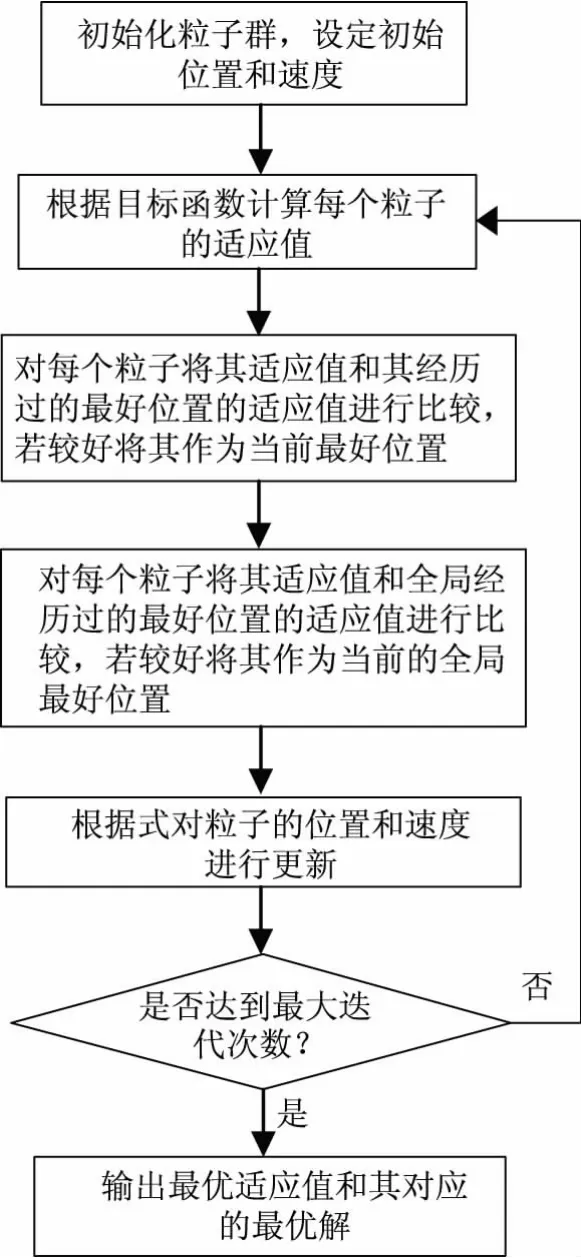
圖2 粒子群算法流程圖Fig．2 Particle swarm algorithm flow chart

2．1．2 粒子群算法在電動汽車充放電調控上的應用

將粒子群算法應用到電動汽車調控第一階段中，由于不同時刻的電價不同，可通過在不同時刻對電動汽車進行充放電操作，使用戶的充電所交電費與放電所得電費得到最優化處理，同時為了保證在第二階段用戶的滿意度，電動汽車電量在第一階段中也不得低于一定的閾值。

圖3為第一階段電動汽車充放電調控模型，首先根據各時段電價，利用粒子群算法確定各個時段充放電的電動汽車數量。再根據電動汽車剩余SOC排序法，對電量剩余多的電動汽車進行放電，對電量剩余少的電動汽車進行充電。下一步進行判斷，如果電動汽車SOC值大于90%則對電動汽車進行放電，如果電動汽車SOC值小于10%則對電動汽車進行充電。若當前時段峰谷差值小于Δf，則對電動汽車進行充電;若當前時段峰谷差值大于等于Δf，則利用電動汽車剩余SOC排序法對電動汽車進行充放電操作。

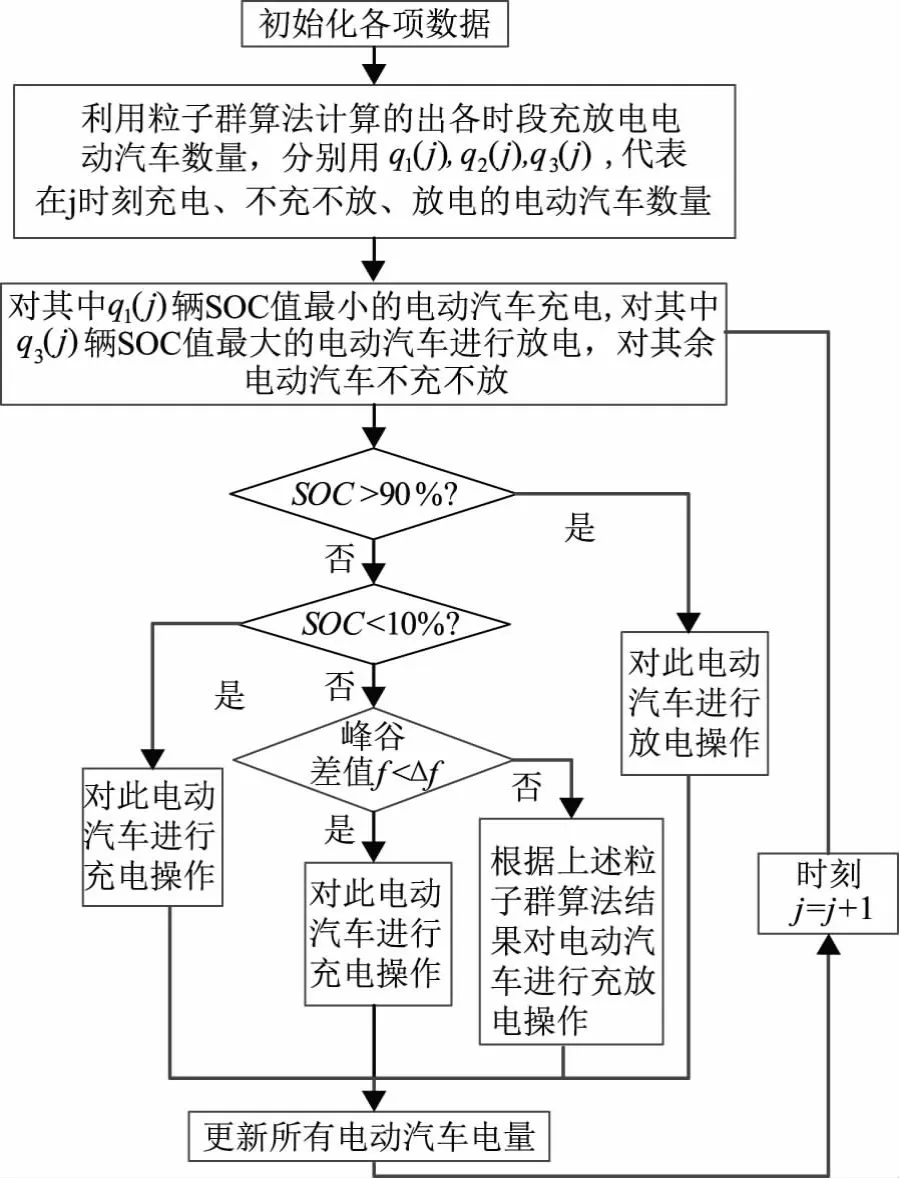
圖3 第一階段電動汽車充放電模型Fig．3 The first stage charge and discharge model of electric vehicle

2．2 第二階段模型

在第二階段模型(見圖4)中，根據用戶所設置的行駛里程，推算出用戶所需電量，再結合當前實際電量算出滿意度值，若滿意度值小于零則對此電動汽車進行充電;若滿意度值大于等于零，則說明電動汽車電量已滿足用戶需求，既不對此電動汽車進行充電也不對此電動汽車進行放電，等待用戶使用。

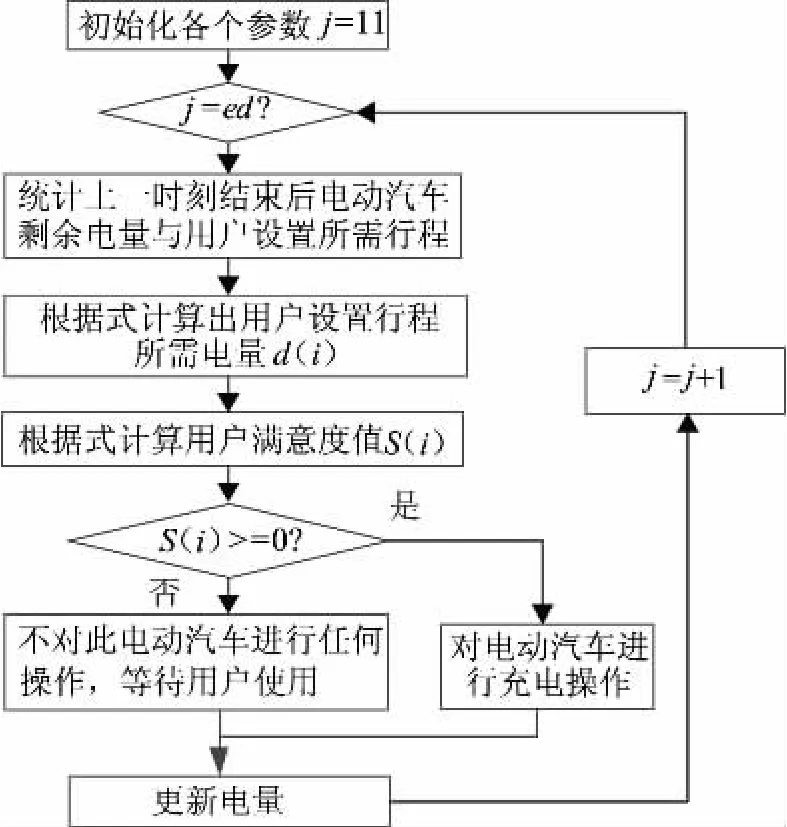
圖4 第二階段電動汽車充放電模型Fig．4 The second stage charge and discharge model of electric vehicle

3 算例分析

3．1 參數的設置

為了驗證二層優化模型對于提升用戶利益的有效性以及提升用戶滿意度的有效性，以北京市某公司員工為例，在07:00～19:00時段對電動汽車充放電進行仿真計算。假設此公司有員工300名，平均每人有一輛汽車，則此公司汽車總數為300輛，其中電動汽車30輛，電動汽車普及率為10%。假設用戶電動汽車充滿電續航里程為200 km，則可根據式(9)計算得出電動汽車SOC值:

式中d需(i)為用戶需求里程;d總為電池充滿電狀態下續航里程。

所提出的粒子群算法，以各時段用戶利益之和作為適應度函數，通過對各個粒子適應度值的對比計算，得出最優解，繼而得到在各個約束條件下用戶的最優利益。其中參數c1=c2=1，進化次數n=200，種群規模s=200，假設每輛電動汽車充放電功率為2．5 kW，電動汽車充電每小時SOC值可增加10%，電動汽車放電每小時SOC值同樣減少10%。

圖5所示為電動汽車初始剩余電量，即電動汽車開始參與調控時的剩余電量;圖6所示為用戶需求里程，在第二階段調控中，可根據用戶需求里程與公式(9)計算出用戶需求電量;圖7為峰谷電價圖，即各個時段的電價。

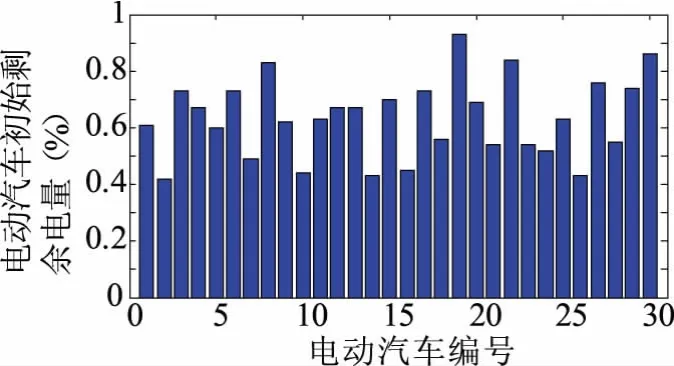
圖5 電動汽車初始剩余電量Fig．5 Initial residual power of electric vehicle

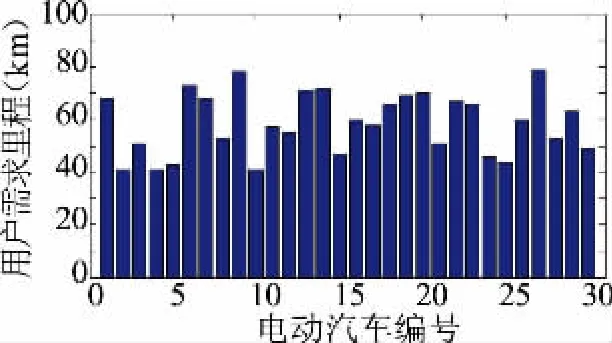
圖6 用戶需求里程Fig．6 Requirements mileage of users

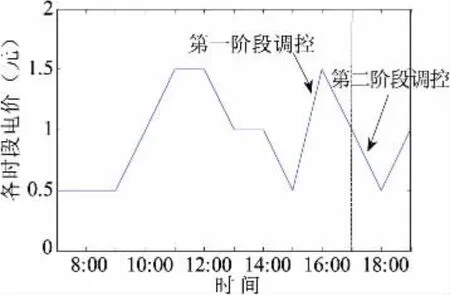
圖7 各時段電價曲線Fig．7 Price curve for each period

3．2 算例結果

3．2．1 第一階段調控算例分析

圖8所示為第一階段中各時段充放電電動汽車的數量，在7:00～9:00期間雖然處于低谷電價，但電動汽車電量都比較充足，此時放電電動汽車占據絕大多數;在10:00～12:00期間，此時處于峰時電價，電動汽車放電可以給電動汽車用戶帶來更多的收益，所以大多數電動汽車仍處于放電狀態;在13:00～16:00期間，此時電價波動比較劇烈(即13:00～14:00為平時電價，15:00為谷時電價，16:00為峰時電價)，而此時電動汽車經過前幾個時段的放電，剩余電量也相應處于較低狀態，因此可以看出，在13:00～16:00時段內，充電電動汽車數量明顯增長。

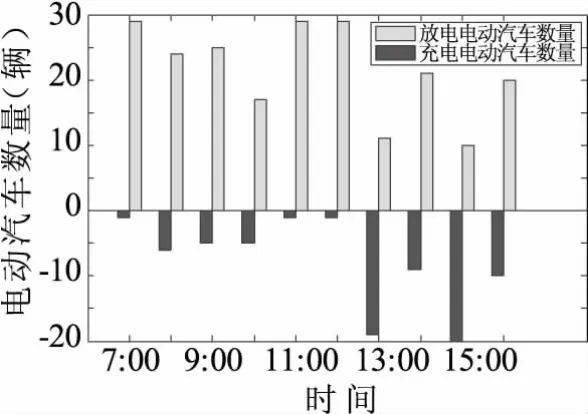
圖8 第一階段控制中充放電電動汽車數量Fig．8 Number of charge-discharge electric vehicle in the first stage

圖9 所示為用戶第一階段控制中負荷曲線圖，實線為調控前負荷曲線，虛線為基于粒子群算法的電動汽車調控策略的負荷曲線，在7:00～10:00，13:00～16:00期間，負荷值都在原有負荷曲線的基礎上略有下降;在10:00～13:00期間，負荷值在原有負荷曲線的基礎上有大幅下降;在可以看出在各個時刻負荷值都有所減少，尤其是在峰值時刻，負荷值減少最為明顯，說明此調控策略在保證用戶利益的基礎上還起到了削峰的作用。

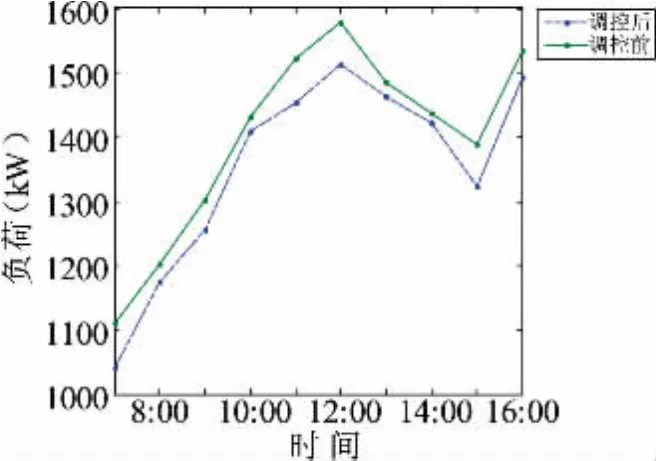
圖9 第一階段控制中負荷曲線圖Fig．9 Load curve in the first stage

圖10 所示為用戶利益曲線，在粒子群算法中隨著迭代次數的增長，各粒子都會不斷向最優值靠近。如圖所示當迭代次數為120次左右時，用戶利益達到最優為159元。

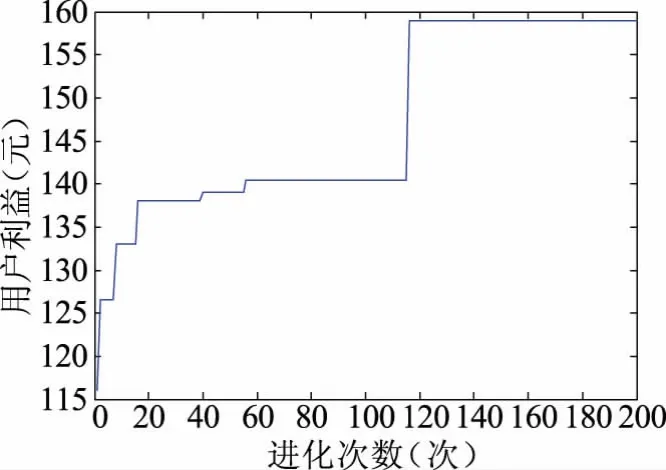
圖10 用戶利益曲線Fig．10 Interest curve of users

圖11 所示為第一階段調控后各個電動汽車剩余電量，為避免過度放電導致的電量過低，電動汽車在第一階段調控結束后剩余電量應保持在10%以上，圖11所示的電動汽車全部滿足要求。

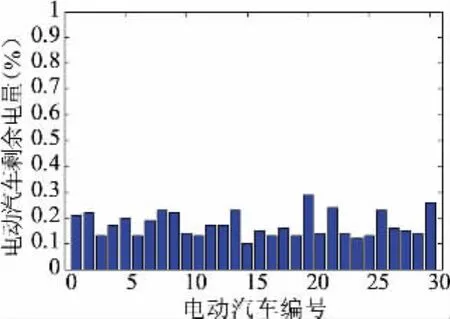
圖11 第一階段結束后電動汽車剩余電量Fig．11 Electric car remaining power after the first stage

3．2．2 第二階段調控算例分析

圖12為第二階段調控后各電動汽車的剩余電量。在經過第二階段調控后，各電動汽車剩余電量與第一階段結束時相比都有一定的提升，剩余SOC值基本保持在20%～50%之間。由于用戶需求電量的差異，導致第二階段充放電調控具有差異性，當電動汽車剩余電量滿足用戶需求電量后，電動汽車就不再充電，同時等待用戶使用;當電動汽車剩余電量不滿足用戶需求時，電動汽車就會持續充電。

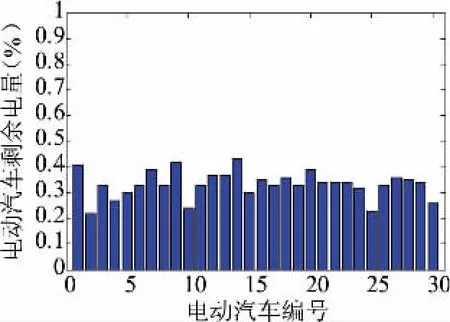
圖12 第二階段調控結束電動汽車剩余電量Fig．12 Electric car remaining power after the second stage

圖13 所示為第二階段調控結束后用戶滿意度值。當用戶滿意度值大于0時，代表用戶處于滿意狀態，電動汽車剩余電量滿足用戶需求;當用戶滿意度值小于0時，則相反。如圖13所示，其中處于滿意狀態的用戶數有27戶，處于不滿意狀態的用戶有3戶，用戶滿意率為90%。由此可以看出第二階段調控可以基本滿足用戶的電量需求。

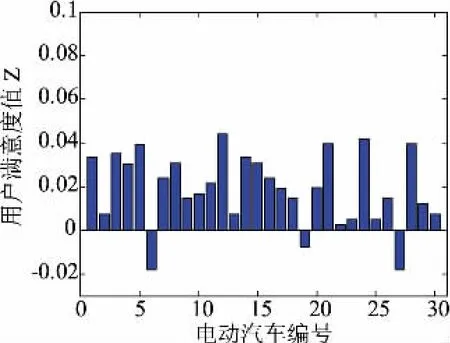
圖13 第二階段調控結束后用戶滿意度值Fig．13 User satisfaction value after the second stage

圖14 所示為電動汽車用戶在參與第一階段、第二階段調控后的收益與花費情況，可以看出每個用戶都可以通過日間放電獲得一定的收益，但用戶都要在第二階段調控中花費少量電費來補充電量，通過第一階段與第二階段調控每位用戶都至少達到不虧損狀態(即總收益為0);這是由于用戶的收益與電動汽車的起始電量有很大關系，當電動汽車起始電量較少時，在峰值電價時電動汽車就不能通過放電來獲得收益;在理想狀態下(即每輛電動汽車的起始電量都在一定的閾值之上)，每位用戶都可以通過對電網反向供電獲得一定的可觀收益。

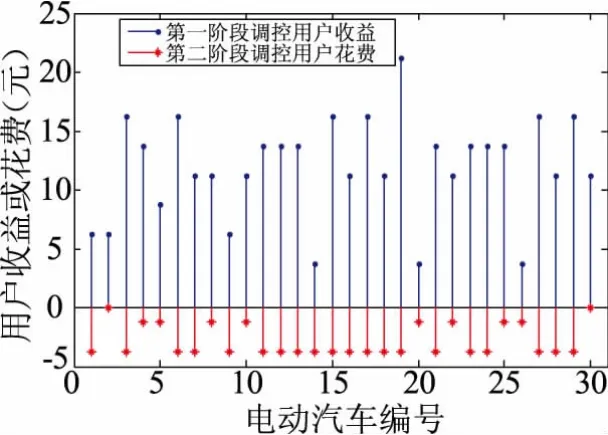
圖14 各用戶收益與花費匯總圖Fig．14 Summary chart of the revenue and expenses for each user

表1所示為各階段電動汽車調控結果，結果顯示第一階段用戶總盈利159元，第二階段用戶總支出85元，合計盈利74元，滿意率達到90%。調控結果說明此算法可以在滿足用戶需求的基礎上，使電動汽車對電網進行反向供電從而獲得收益，既保證了用戶的需求又維護了用戶的收益。

表1 調控結果Tab．1 Control results

表2所示為第二階段調控電動汽車充放電情況，其中1代表放電，0代表不充也不放，－1代表充電，可以看出在第二階段主要是對電動汽車進行充電調控，為了滿足用戶的用電需求，在第二階段調控中對電量不足的電動汽車進行充電操作。

表2 第二階段調控電動汽車充電情況Tab．2 Regulation of electric vehicle charging situation in the second stage

4 結束語

為了提高用戶收益并滿足用戶用電需求，考慮電動汽車剩余電量與負荷峰谷差值，利用粒子群算法對電動汽車進行充放電調度:以電動汽車用戶利益最佳化為目標，對電動汽車充放電過程進行了計算。仿真結果說明:

(1)經過在第一階段調控中粒子群算法對電動汽車的有序充放電調控，用戶在獲得一定收益的基礎上電動汽車還保持有一定的剩余電量;

(2)經過第一階段粒子群算法對電動汽車的有序充放電調控，各時段負荷值得到明顯削減，并且負荷峰谷差值得到削減;

(3)經過第二階段的充電調控，90%的用戶對電動汽車剩余電量滿意，并且綜合兩個階段調控，用戶還可獲得一定量收益。可以說明此算法既可以使用戶得到一定的收益，又能滿足用戶的用電需求。