單頂點多折痕折紙形式啟發的空間折展機構

廣晨漢，劉 迎，楊 洋

(北京航空航天大學機械設計及自動化系，北京 100191)

0 引 言

受運載火箭整流罩尺寸的限制，衛星的一些功能部件(如：天線等)需在衛星發射時折疊收納待衛星入軌后展開。折疊收納及展開的動作主要依靠折展機構實現。現階段對折展機構的研究主要集中在大口徑空間構架式可展天線機構上[1-5]，其主要思路是通過對已有的平面或空間機構單元進行組合而構成大型可展機構，展開金屬網面天線。而近年來，適用于小衛星的固體反射面天線機構的研究則較少[5-6]。

折紙是一種將二維平面折成三維結構的藝術形式，折紙的變形特征對折展機構的研究提供了一種新的思路。已有的基于折紙的空間折展機構的研究主要集中在空間可展天線及空間可展太陽能電池板上。文獻[7-8]介紹了一種基于flasher折紙形式的可展太陽能陣列。文獻[9]介紹了一種將flasher折紙形式剪切后衍生出的，可用作可展太陽能電池板的可展陣列。文獻[10]展示了一種通過去除flasher折紙形式中的一組或兩組中心對稱單元，使其在處于展開狀態時形成近似拋物面的可展拋物面天線。基于flasher折紙形式，文獻[11]展示了一種利用折疊時儲存的材料變形能進行展開的薄殼可展天線。

上述文獻介紹的折展機構幾乎都需要借助額外的單自由度機構輔助展開，這對于較大的空間設備是可以接受的。但是對于結構需要精簡的小衛星，需要避免添加額外機構。

文獻[12-13]介紹了一種由Flasher折紙形式啟發的多瓣式可展固體反射面天線。其不需要額外的驅動機構，但所需的驅動器數量較多，且結構較為復雜，故不適用于小衛星。文獻[14]展示了一種單頂點多折痕折紙形式啟發的可將平面結構折疊的空間折展機構，可用于可展太陽能電池板。此機構結構及構型簡單，只需一個驅動器就可完成自身展開，因此非常適用于小衛星。

進一步研究發現，文獻[14]中論述的機構，不僅能將平面結構折疊，還能將可包絡回轉曲面的錐形結構折疊。但是，文獻[14]中僅介紹了可將平面結構折疊的可展機構扇頁部分在折疊與展開狀態下的幾何設計模型，并未提出可將錐形結構進行折疊的可展機構扇頁部分在折疊與展開狀態下的幾何設計模型。

針對上述問題，對受單頂點多折痕折紙形式啟發的空間折展機構的構型進行介紹，并展示了此類機構也可將包絡回轉曲面的錐形結構進行折展。然后，本文提出了可將錐形結構進行折疊的可展機構扇頁部分在折疊與展開狀態下的幾何設計模型。最后，對此幾何設計模型及平面折疊幾何設計模型進行了近似簡化，使其可以便捷地驗證機構的幾何設計是否滿足約束條件，并通過算例計算進行了驗證。

1 機構構型

單頂點多折痕折紙形式是一種常見的折紙形式，如圖1所示。圖1中實線折痕為峰折痕，虛線折痕代表谷折痕，兩種折痕代表著不同(相反)的折疊方向。

若將圖1中的每相鄰兩條折痕所夾的紙認為剛體，將折痕認為轉動副，則圖中的機構本質上為球面機構，自由度并不為1。同時，圖1中紙的厚度被認為是0，但在實際中，并不存在厚度為0的物體。

因此，對紙增添厚度并對機構進行調整，得到了如圖2的折展機構。此機構的自由度為1。文獻[14]運用旋量的方法[15-16]對此機構的單自由度特性進行了證明。

每個機構單元由5個構件組成，如圖2所示。構件1及構件2為圓心角(圓心角α=π/n)相等的兩片扇頁，這兩個構件鉸接。構件1與構件3之間通過圓柱副連接，構件2與構件4之間亦通過圓柱副連接。每個扇頁上的鉸鏈軸線與圓柱副軸線間的關系為空間互異。構件3與構件4都鉸接在構件5(基座)上。此機構單元的自由度為1，因此此機構單元圓周陣列構成的整個機構(共有2n片扇頁)的自由度亦為1。

如圖3所示，若保證一份扇頁上的圓柱副的軸線與鉸鏈的軸線成異面直線的關系，將平面扇頁(完整圓平板的1/2n等份)替換為圓錐扇頁(完整圓錐板的1/2n等份)，甚至將圓錐板的上表面加工為回轉曲面(例如可展天線中常用的拋物面)，都能按照此機構的方式展開，如圖4所示。圖4中，機構扇頁的上表面都被處理為拋物面，展開后可用作小衛星的折展天線。

2 幾何模型

機構處于折疊狀態與展開狀態的幾何模型是判斷機構能否滿足設計要求的依據，同時也是計算折展比的基礎。為此對機構處于折疊狀態與展開狀態的幾何模型進行建模。為快速、便捷地判斷設計是否滿足約束條件，將幾何模型進行近似簡化。

本文中只考慮扇頁部分在折疊時與未折疊時的幾何模型。其他構件的幾何設計可在扇頁部分幾何模型確定后進行。

2.1 無錐度模型

折展機構展開狀態的折展機構的大徑為2R，小徑為2r，展開狀態的高度與扇頁的厚度相等，即Hunfold=h。以n=10為例，如圖5。

折疊后，內孔為截面為正n邊形的棱柱，如圖6。正n邊形的邊長為l=2h。

折疊后的機構的中心孔內切圓半徑為：

(1)

機構外接圓半徑為：

(2)

機構的整體高度為：

Hfold=R-cosα

(3)

將式(2)對n求導數，可得：

(4)

式(4)的形式較為復雜，故對其進行近似簡化。在實際設計時，一般R>>h，即：

rout=rin+Rsinα

(5)

將式(5)對n求導數，可得：

(6)

2.2 有錐度模型

展開狀態的折展機構的大徑為2R，小徑為2r，展開狀態的高度為Hunfold，板的厚度為h，錐角為π-2β。以此為例，各塊之間鉸接，組成一個封閉環，如圖7。

如圖8所示γ為機構展開時其中一份的面ABCD(面2)與側面CDFE(面3)所夾的二面角。

可求得：

(7)

其中，面ABCD(面2)與機構俯視平面xOz(面1)所夾的二面角為θ，即：

(8)

折疊后，內孔截面為2n邊形的棱柱，如圖9。2n邊形的邊長為h。

折疊后的機構的中心孔內切圓半徑為：

(9)

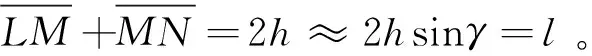
所以，折疊后的機構的中心孔內切圓半徑可近似為：

(10)

機構外接圓直徑為：

(11)

或

(12)

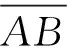
機構的整體高度為：

(13)

實際設計中，一般R>>h、τ≈α且γ≈90°，則有：

(14)

(15)

Hfold=secβ(R-rcosα)

(16)

將式(15)對n求導數，可得：

(17)

2.3 近似幾何模型

比較式(17)與式(6)，發現只相差secβ。當β=0°時，secβ=1，可將式(6)與式(17)統一為：

(18)

(19)

可求得在一定條件下使rout最小的n。而n為不小于3的整數，故需求得n(在實際設計時，機構的扇頁數盡量少)。這樣使機構外接圓直徑rout最小的nmin為：

nmin=n

(20)

同時發現，式(16)與式(3)，式(15)與(5)也只相差secβ，這樣無錐度與有錐度的折展機構的設計方法可統一，結果見表1。

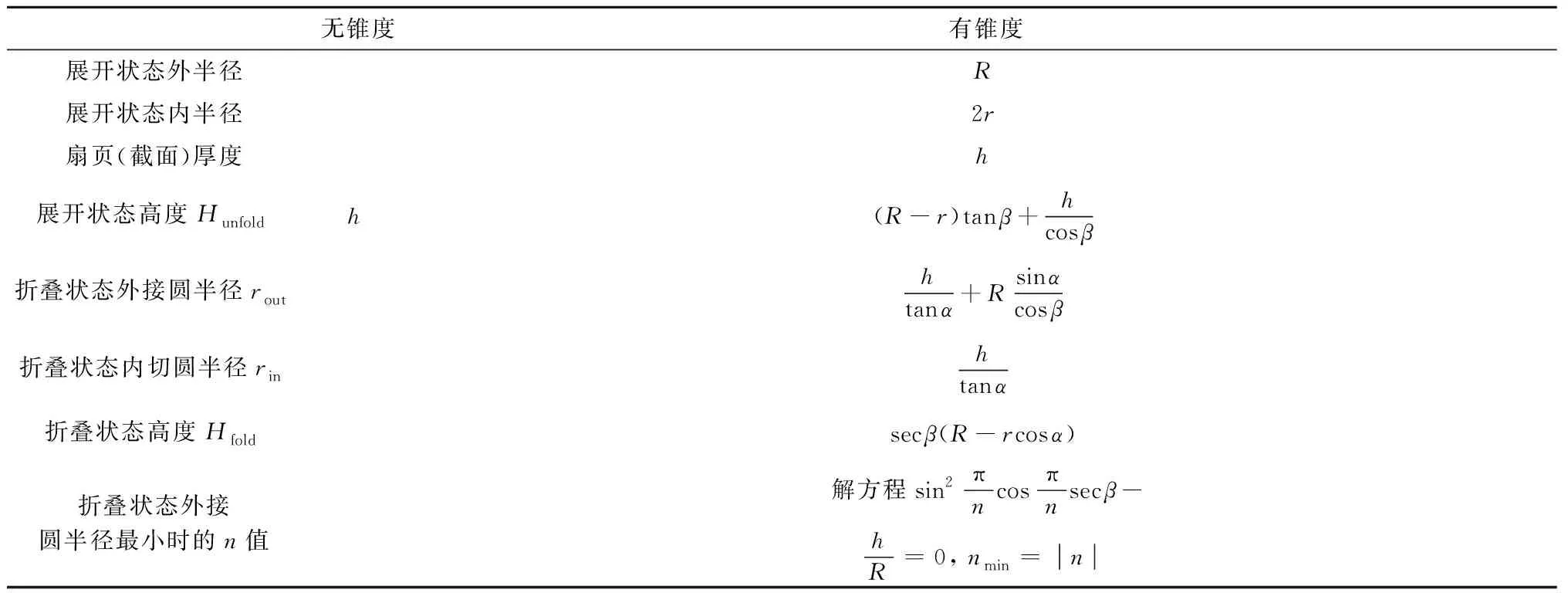
表1 近似幾何模型Table 1 Approximate geometry model

3 算例與誤差校驗

本章中列出一組設計尺寸，如表2所示，以展示rout、rin及Hout的隨n的變化趨勢，以及近似模型與解析模型的誤差。

表2 設計尺寸Table 2 Designing dimensions

3.1 無錐度模型的尺寸變化趨勢及誤差

將表2中的數據帶入式(1)、式(5)及式(3)中，并通過式(18)求得nmin，結果如圖10及圖11。

將式(2)與式(5)作差，并取絕對值，繪制出近似后的折疊狀態外接圓半徑rout與理論的折疊狀態外接圓半徑rout的誤差變化曲線，如圖12。可以發現，在近似條件下，誤差很小，可以忽略。

從圖10可以看出rout的變化曲線實際上是內凹的，存在使rout最小的點。同時，在接近最小值點的曲線段上的斜率值較小且變化平緩，在實際設計時，在rout滿足要求的情況下，可以盡量選更小的n值，使扇頁數盡量少。

圖11展示出與直觀理解不同的現象，rin不是固定的，會隨著n的增大而增大。這意味著折疊后的機構的中心孔可以被利用，容納某些功能結構，如：空間可展天線的次鏡等。

在Rh(約R>10h)時，如圖12所示，近似模型對rout引入的誤差相對于rout非常小，可以忽略不計。所以在實際設計時，可以直接采用近似模型來進行設計。

3.2 有錐度模型的尺寸變化趨勢及誤差

將表2中的數據代入式(10)、式(12)及式(13)中，并通過式(18)求得nmin，結果如圖13及圖14。

如圖13所示，有錐度模型的rout的變化趨勢一致，存在使rout最小的點。在實際設計時，選取n的思路與無錐度模型的一致。

如圖14所示有錐度模型的rin的變化趨勢與無錐度模型的一致。

將式(10)與式(14)作差，式(12)與式(15)作差，式(13)與式(16)作差并取絕對值，繪制出近似后的rout與理論rout的誤差變化曲線，近似后的rin與理論的rin的誤差變化曲線，近似后的Hfold與理論的Hfold的誤差變化曲線，如圖15。可以發現，在近似條件下，rout誤差及的rin誤差很小，可以忽略。而rout的誤差在n=18時大約為6.7%，并且近似值大于非近似模型值。意味著在Rh(約R>10h)時，近似幾何模型可以快速判斷機構的幾何尺寸是否滿足設計要求。

3.3 折展比

折展比是反映機構折展能力的重要參數。折展比又分為徑向折展比和軸向折展比。徑向折展比定義為：

(21)

軸向折展比定義為

(22)

對無錐度展開模型的算例，如圖10所示，其nmin=17。此時，rout=887 mm,Hfold=2107 mm，將其帶入式(21)及式(22)分別計算出徑向折展比λr=0.355及軸向折展比λa=0.421。

對有無錐度展開模型的算例，如圖13所示，其nmin=18。此時，rout=955 mm,Hfold=2432 mm，將其代入式(21)及式(22)分別計算出徑向折展比λr=0.382及軸向折展比λa=0.486。

文獻[5]中介紹的可展固體反射面天線的徑向折展比在0.36～0.44之間，軸向折展比在0.37～0.54之間。本文所介紹的折展機構的折展比在算例幾何尺寸條件下持平于現有的可展天線的折展比，當h/R更小時，機構的折展比會優于現有可展天線的折展比，說明此機構在可展天線方面有一定的應用潛力。

4 結 論

單頂點多折痕折紙形式啟發的空間折展機構構型不僅可將平面結構進行折展，也能將可包絡回轉曲面的錐形結構進行折展。

介紹了此類機構處于展開狀態及折疊狀態的幾何設計模型，并在工程應用所允許的范圍內對其進行了近似簡化，可以快速判斷設計是否滿足尺寸約束條件。

通過算例發現有錐度的模型與無錐度模型都具有使折疊狀態下機構外接圓半徑值最小的最小值點(nmin)。同時，機構的折展比與現有的空間可展固體反射面天線的折展比相當，甚至更優。