基于車輛前方目標運動模型的主動避撞系統的研究
盤朝奉,丁亞強,江浩斌,b
(江蘇大學 a.汽車工程研究院; b.汽車與交通工程學院, 江蘇 鎮江 212013)
近年來,汽車行業的飛速發展以及國民購買能力的提高帶動了汽車銷量的增加,但也不可避免地提高了交通事故發生的可能性。研究表明:如果提前0.5 s示警駕駛員,60%的追尾事故可以避免[1]。從保護人身安全和降低交通事故發生的可能性的角度出發,研制出能在兩車有碰撞危險時及時提醒駕駛員采取相應的措施,甚至對汽車進行主動干預、自動采取緊急制動措施進行有效避撞的汽車主動避撞系統(collision warning system)顯得至關重要。而如何有效、精準地獲取車輛前方目標的有效信息,并通過對前方目標的跟蹤預測其下一步的運動狀態,則成為當前研究的熱點。
2017年博世展出了一輛配置主動避撞系統等先進自動駕駛技術的自動駕駛汽車,其可以在低速狀態下實現主動避撞[2]。沃爾沃公司開發的避撞控制系統能基于前方移動目標車輛信息實現自動走-停巡航控制,控制車輛的自動剎車和驅動,實現主動避撞[3]。江蘇賽博公司與高校合作也研制出了擁有多目標識別能力的毫米波雷達,可以很好地運用于車輛復雜環境防撞系統[4-6]。
汽車行駛過程中受路面形狀、附著系數以及汽車自身參數等多重因素的影響,在通過毫米波雷達跟蹤前方目標時不可避免地會出現目標識別錯誤和漏警的情況。建立與前方機動目標的實際情況相符合又便于數學分析處理的目標運動模型可以很好地跟蹤目標而不會造成目標的丟失[7-8]。本文通過對汽車運動規律的分析和毫米波雷達的障礙物檢測機理,對傳統的卡爾曼濾波算法進行簡單介紹,比較了常速度模型、常加速度模型以及當前統計模型的系統原理及應用場合。根據城市道路車輛行駛的實際情況,通過對幾種目標機動模型算法的仿真分析,選取了當前統計模型作為機動目標模型,并采用了基于當前統計模型的自適應卡爾曼濾波算法對車輛前方目標進行跟蹤。選取一種臨界安全距離模型,在此基礎上建立主動避撞仿真模型,搭建實車實驗平臺,通過實車實驗再一次驗證了算法的可行性。
1 目標跟蹤模型
車輛行駛過程中自車與前方障礙物目標是存在相對運動的,目標跟蹤算法需要實時得到前方障礙物目標的位置、速度及加速度等狀態信息,精確地識別前方目標并準確判斷目標距離,這有利于防碰撞功能的實現。
目前主要的跟蹤模型主要有目標類似勻速運動的勻速運動模型(CV)、目標類似勻加速的勻加速運動模型(CA)和能應用于多種目標運動模型的 Singer 模型,后來在 Singer 模型的基礎上又提出了當前統計模型,下面主要介紹常用于車輛跟蹤的當前統計模型[9-11]。
勻速運動模型和勻加速運動模型都是研究目標相對規律運動的狀態,對目標運動狀態的研究都有一定的局限性。如果當目標做不規律運動時,它的加速度在緊鄰的下一刻不會發生太大的突變,即只能取在“當前”的加速度的某一個鄰域內的有限值,這即為當前統計模型提出的根據。其表達式如下:


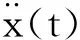

由此可以得出當前統計模型的狀態空間方程:

(4)
選取狀態變量
(5)
假設采樣周期為T,需要對上式進行離散化,由此可得到當前統計模型的離散狀態方程:
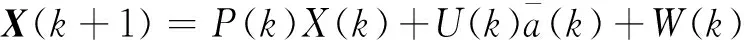
(6)
相應的觀測方程為:
Z(k)=HZ(k)+V(k)
(7)

狀態轉移矩陣為:

式中:Z(k)為觀測向量;H為觀測矩陣。
輸入矩陣:


2 卡爾曼濾波算法
目前用于目標跟蹤的算法很多,其中,卡爾曼( Kalman )濾波算法因能結合車輛行駛的特點,對車輛跟蹤的效果比較穩定,所以普遍應用于車輛目標跟蹤領域。
設跟蹤系統過程的離散隨機差分方程描述為
X(k)=AX(k-1)+BU(k-1)+W(k-1)
(16)
系統的觀測方程為:
Z(k)=HX(k)+V(k)
(17)
式中:Z(K)為k時刻的量測值;H為系統的測量矩陣;V(K)為系統量測高斯白噪聲。
卡爾曼濾波的數學模型如下:
1) 狀態變量預測方程:
X(k|k-1)=AX(k-1|k-1)+BU(k)
(18)
2) 協方差矩陣預測方程:
P(k|k-1)=AP(k-1|k-1)AT+Q
(19)
3) Kalman增益矩陣方程:
Kg(k)=P(k|k-1)HT/[HP(k|k-1)HT+R]
(20)
4) 狀態變量最優化方程:
X(k|k)=X(k|k-1)+Kg(k)[Z(k)-HX(k|k-1)]
(21)
5)協方差最優更新方程:
P(k|k)=[1-Kg(k)H]P(k|k-1)
(22)
式(18)~(22)中:X(k|k-1)為通過前一狀態預測的結果;X(k-1|k-1)為前一狀態通過運算得到的最優結果;U(k) 為當前狀態的控制量;P(k|k-1) 為X(k|k-1) 為當前狀態相對應的協方差矩陣;P(k-1|k-1) 為X(k-1|k-1) 對應的協方差矩陣;AT為A的轉置;X(k|k) 表示現在狀態的最優估計值;Kg(k) 為當前狀態的卡爾曼增益;HT為H的轉置。
卡爾曼濾波主要由2部分組成:一為時間更新方程,即步驟 1)和 2),計算得出狀態變量的一步預測以及相應的預測協方差矩陣,得到的協方差矩陣可作為下一時刻的狀態估算;二為狀態更新方程,即 第3)~ 5)步,通過第1部分中得到的狀態變量的預測以及相應的預測協方差矩陣和當前狀態的觀測值,計算得出當前狀態的后驗估計。
3 仿真模型的建立
車輛在道路上直線行駛時,一般有以下幾種行駛模式:勻速或接近勻速、勻加速或勻減速(或接近勻加速勻減速)以及變加速變減速。因為正向的減速可以當作反向的加速[13],因此本文將減速運動與加速運動看作同一種運動情況,統一以加速代替。所以主要設計了以下幾種仿真工況:車輛勻速運動、車輛勻加速運動以及車輛變加速運動。分別對常速度模型、常加速度模型以及當前統計模型的卡爾曼濾波算法估計結果進行了對比分析。圖1為目標運動仿真模型。

圖1 目標運動仿真模型
3.1 車輛勻速運動
將車輛看作勻速運動,分別對車輛的當前統計模型、CA模型和CV模型的卡爾曼濾波算法進行仿真分析,設置兩車仿真距離為60 m,以相同的速度同向直線行駛,隨著時間的變化,可得到兩車的位移和速度曲線,見圖2、3。

圖2 勻速運動時各模型跟蹤相對距離的仿真結果

圖3 勻速運動時各模型跟蹤相對速度的仿真結果
由仿真結果可得:車輛在勻速跟車時,當前統計模型和常速度模型跟蹤算法較為精確,常加速度模型跟蹤算法誤差較大。
3.2 車輛勻加速運動
將車輛看作勻加速運動,分別對車輛的當前統計模型、CA模型和CV模型的卡爾曼濾波算法進行仿真分析,設置兩車仿真距離為60 m,同向直線行駛時,自車速度為30 km/h,加速度為1 m/s2,前車速度為20 km/h,加速度為1.5 m/s2,隨著時間的變化,可得到兩車的位移和速度曲線,見圖4、5。
由仿真結果可得:車輛在勻加速跟車時,當前統計模型和常加速度模型跟蹤算法較為精確,常速度模型跟蹤算法誤差較大。

圖4 勻加速運動時各模型跟蹤相對距離的仿真結果
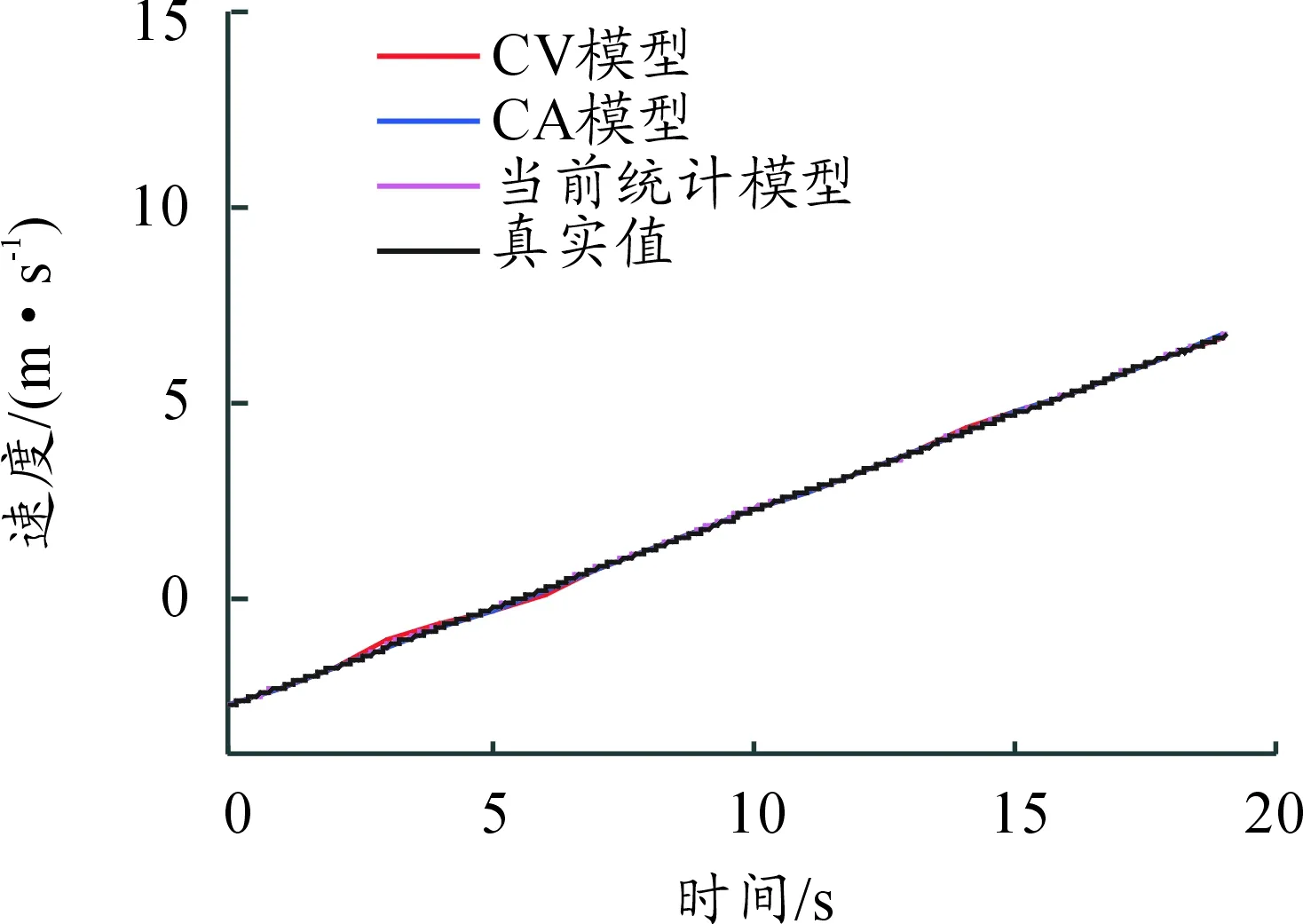
圖5 勻加速運動時各模型跟蹤相對速度的仿真結果
3.3 車輛變加速運動
由上述兩個仿真模型分析可以看到:常速度模型的卡爾曼濾波跟蹤算法適用于車輛勻速運動,常加速度模型的卡爾曼濾波跟蹤算法適用于車輛勻加速運動,而當前統計模型的卡爾曼濾波跟蹤算法則可適用于兩種形式的車輛運動狀態。車輛在道路上行駛時,不止會有前兩種運動狀態,還可能會進行變加速運動等不規則運動,因此本文建立相關跟蹤模型進行進一步的仿真分析。
將車輛運動看作變加速運動,分別對車輛的當前統計模型、CA模型和CV模型的卡爾曼濾波算法進行仿真分析,設置兩車仿真距離為50 m,同向直線行駛時,自車做速度為30 km/h 的勻速運動,前車初速度為20 km/h,在前5 s內做勻速運動,在5~10 s內做加速度為2 m/s2的勻加速運動,在 10~15 s內做加速度為-1 m/s2的勻減速運動,然后在 15~20 s內做勻速運動,隨著時間的變化,可得到兩車的位移和速度曲線,見圖6、7。

圖6 變加速運動時各模型跟蹤相對距離的仿真結果

圖7 變加速運動時各模型跟蹤相對速度的仿真結果
通過對車輛的3種運動狀態的仿真結果可以看出:相對于常速度模型和常加速度模型的卡爾曼濾波算法,基于當前統計模型的卡爾曼濾波跟蹤算法可以更精確地跟蹤前方目標,在車輛正常行駛時可以很好地達到穩定的跟蹤效果,且相對誤差較小。
3.4 安全距離模型
假設車輛在制動時能全力制動,引入臨界安全距離模型,對跟蹤效果進行進一步分析。安全距離模型見圖8。
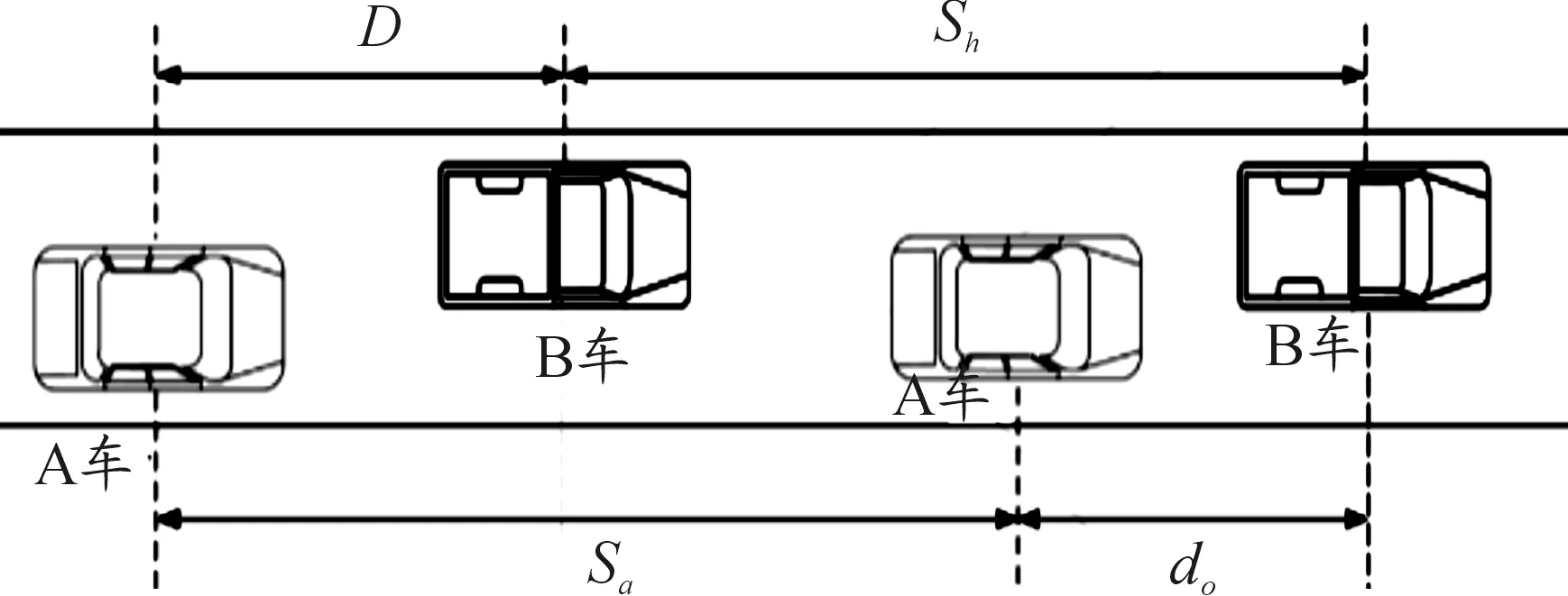
圖8 安全距離模型示意圖
如圖8所示,當兩車同向行駛且前車在后車的正前方時,兩車在A車制動的剎那相距為D。A車制動一段時間后,行駛距離為Sa,B車的行駛距離為Sb,這時兩車間的距離為d0。安全距離的公式為
D=Sa-Sb+d0
(23)
臨界安全距離可表示為
式中:amax為自車最大制動減速度,一般數值取6~8 m/s2;d1為自車停止后與前方目標車輛之間的車間距,一般取1~2 m;v1和vrel分別為自車制動前的初始速度和相對前車的速度[14-15]。
3.5 主動避撞仿真模型
為了進一步驗證本算法的雷達的跟蹤效果,基于本算法建立了主動避撞模型,見圖9。
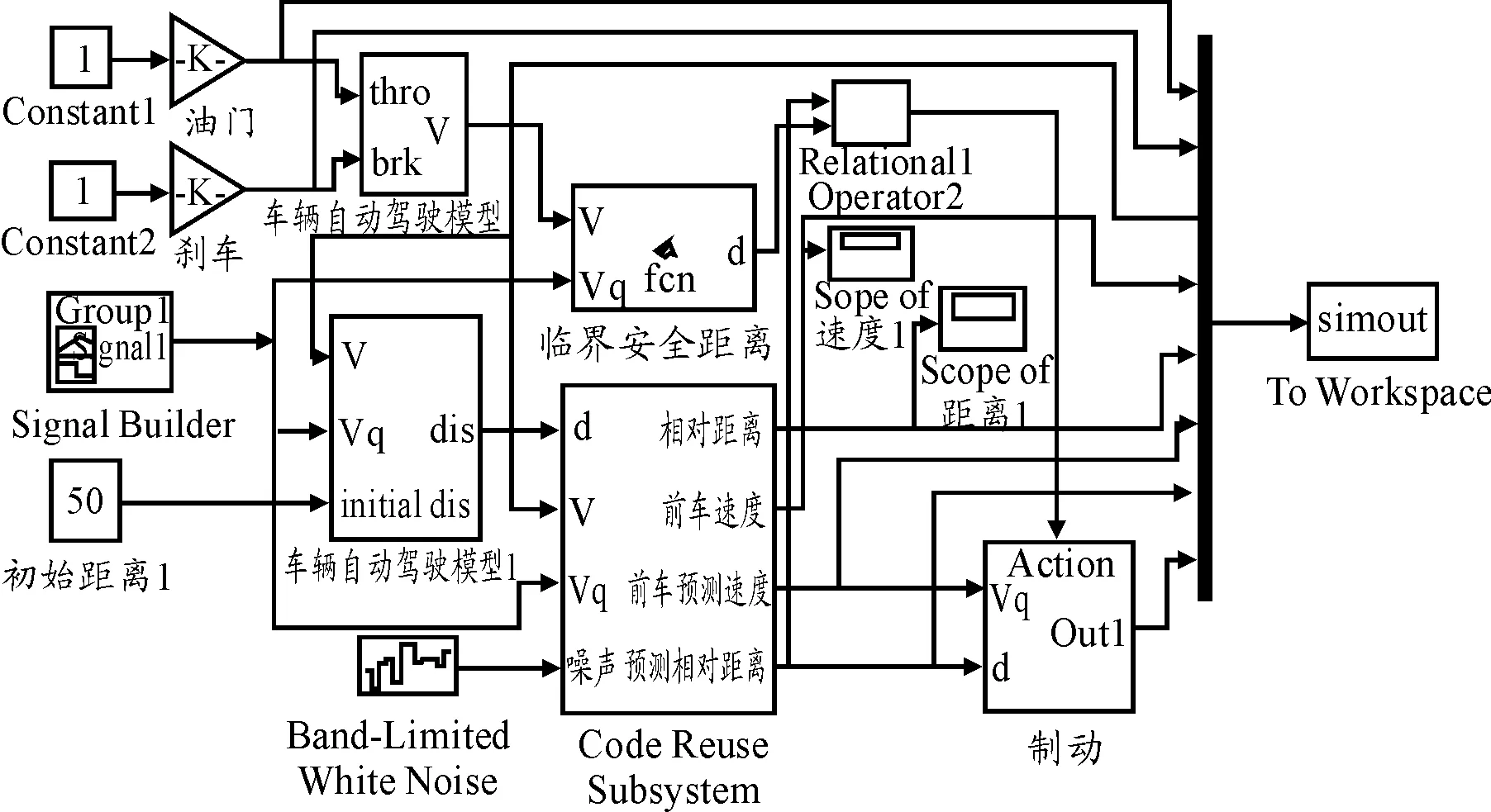
圖9 主動避撞仿真模型
4 實車實驗驗證
為了驗證所引用的安全距離模型的有效性以及本算法的跟蹤效果,基于中距離雷達對主動避撞系統進行實車實驗。根據中國新車評價規程標準測試工況,在天氣晴朗的情況下,進行了實車驗證。實驗設備見表1。
表1 實驗設備

目標車試驗目標車運動目標車車載設備毫米波雷達執行器控制器其他設備Canape11.0線束CancaseOBD線
上位機采用 MicroAutoBox II 控制器作為通信網關,實現上位機數據收發。測控上位機 PC 采用光纖以太網與 MicroAutoboxII 連接,并擁有CANCase及其他設備的預留接口。CANCase用于實時在線觀測雷達數據,完成數據采錄工作,可通過canape讀取數據,且可以轉換為.mat格式,通過Matlab 分析數據。本次實驗采用的是國內某款車型,該車匹配有博世第 9 代 ESP 系統,能作為自動緊急制動系統的執行器。圖10 為移動目標車。

圖10 移動目標車
實驗中,運動目標是支撐架下的反射棱鏡,該三棱鏡有3個面,3個面之間角度為 90°,這樣的尖銳直角結構對于雷達波有非常強的反射效應。實驗測試證明,該三角棱鏡可以代替車輛作為雷達反射目標。使用該移動目標進行測試實驗的優點是測試方便、反復使用性強。但基于安全起見,只進行了自車30 km/h對前車10 km/h以及20 km/h的工況實驗,所得結果與仿真結果的對比分析如圖11、12所示。

圖11 前車速度為10 km/h時隨時間變化的距離

圖12 前車速度為20 km/h時隨時間變化的距離
兩個實驗結果均表明:基于當前統計模型的卡爾曼濾波算法的實車實驗結果與仿真結果趨勢完全一致,車輛在到達臨界安全距離時制動,避免了碰撞,表明所建立的仿真模型是可靠的。
5 結束語
本文對車輛前方目標的跟蹤采用了3種仿真工況,最后仿真對比分析得到了當前統計模型卡爾曼濾波跟蹤算法能實現各種工況下的精確追蹤的結論。使用該算法,建立一種臨界安全距離模型,通過實車實驗,對該算法進行進一步的驗證。對實驗所得數據進行分析,證明該算法能精確跟蹤前車,且避免了車輛碰撞,再次驗證了該算法的可行性。但本文只驗證了前方移動目標的跟蹤效果,接下來對車輛前方靜止目標的主動避撞效果還需進一步的驗證。

