淺析電子商務影響因素的模型
——以天貓“雙十一”為例
歐雄輝 劉洋
廣東海洋大學數學與計算機學院
2009年11月11日,天貓(原淘寶商城)出于讓大眾記住淘寶商城和網上促銷活動能不能吸引消費者進行消費的目的,在“雙十一”這一天做了一個屬于“淘寶商城”的節日,可未曾想到大獲成功。從2009年只有27個品牌參加,銷售額只有5000萬元到如今高達1000多個品牌參加,銷售額達到1682億元,短短八年時間銷售額翻了三千多倍[1]。本文以天貓“雙十一購物狂歡節”(下文簡稱“雙十一”)銷售額增長的原因為例,采用廣義線性模型、多元回歸模型與曲線估計進行組合分析,提出了一個新的模型。
一、數學方法
廣義線性模型[2]由三部分組成:
(1) 系統參數,即線性預測量:
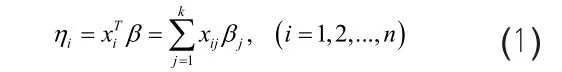
(2) 隨機變量yi是滿足廣義線性模型的指數分布族的隨機樣本。
(3) 連接函數:
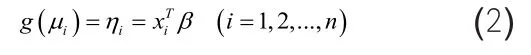
隨機變量y與相關變量xi之間的概率模型為[3]:

其中y-被解釋變量,xi-解釋變量,ε-隨機誤差項,βi-回歸系數。
二、實例分析
W--“-雙十一”交易額;
X1---社會物流總費用;
X2---社會物流總額;
X3---手機網民的數量;
X4---教育投入;
X5---城鄉差距。
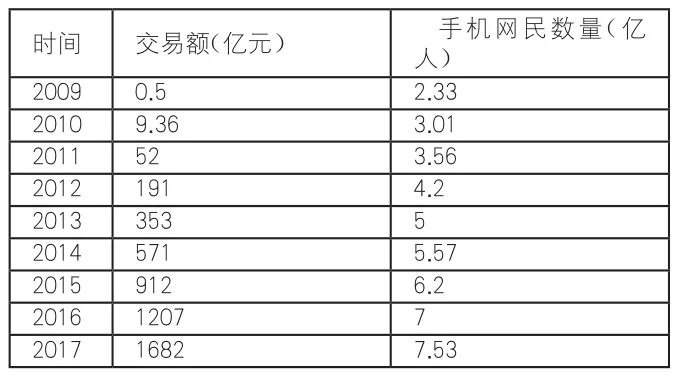
表1 歷年“雙十一”交易額與手機網民數量
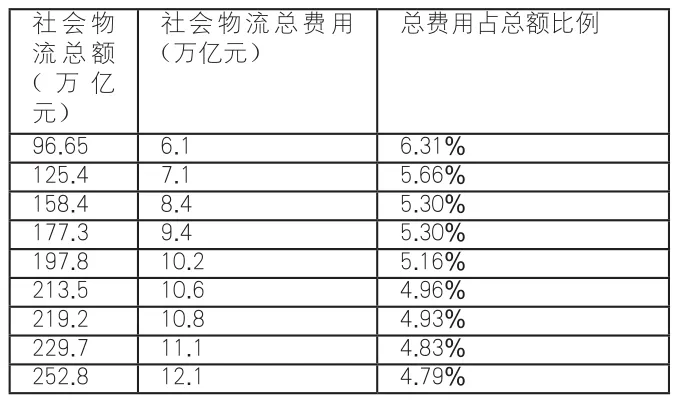
表2 社會物流相關數據
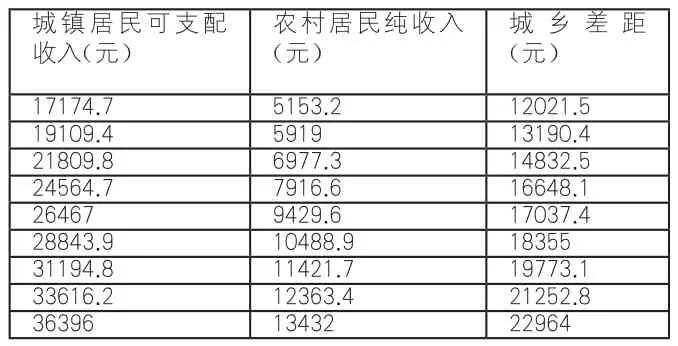
表3 城鄉差距
運用單一樣本K-S檢驗對被解釋變量W的正態性進行檢驗,得到漸進顯著性P值為0.2,大于所設定的顯著性水平0.05,可以認為W這組數據服從正態分布。
為了減少數據造成的不可觀測的誤差,對數據進行Box-Cox變換。然后對變換后的W與X1,X2,X3,X4,X5這5個因素進行多元逐步線性回歸,得到X4與X5的t值的絕對值分別為9.334和3.726,sig值為0和0.01,它們的sig值均小于0.05,表示它們與轉換后的W差異顯著;R值、R平方、調整后的R平方分別為0.999、0.998和0.998,擬合優度非常高。故得出的模型為:

由于W服從標準正態分布,所以σ2=1,故W的概率密度為:
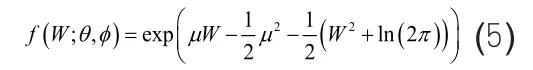
連接函數為:
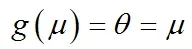
因為Wi服從標準正態分布,所以服從線性回歸模型:
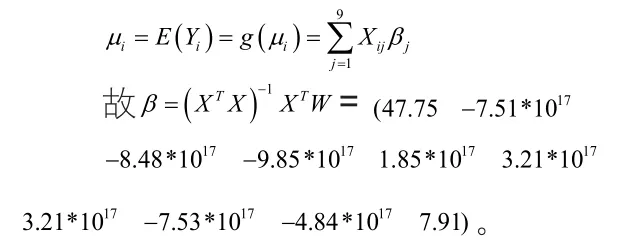
所以得到的廣義線性模型為:

而社會物流費用率與交易額的指數型曲線回歸模型為:

綜合(4)(6)(7)得交易額模型:
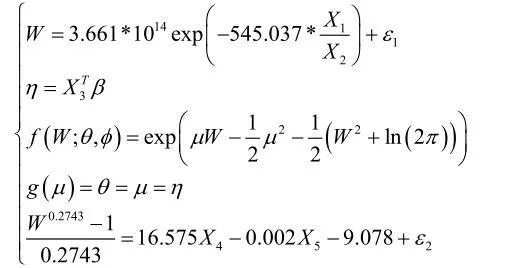
以上為城鄉差距、物流、教育投入與手機網民數量對“雙十一”交易額的影響模型。

