城市可持續(xù)發(fā)展中的止贖房產(chǎn)處置模式研究
郭 頌
(上海財(cái)經(jīng)大學(xué) 金融學(xué)院,上海 200433)
目前,隨著我國(guó)住房規(guī)模的持續(xù)擴(kuò)張和經(jīng)濟(jì)增長(zhǎng)的換擋,已出現(xiàn)了諸如“鬼城”“空城”等泡沫化現(xiàn)象,住房貨款違約風(fēng)險(xiǎn)成為城市發(fā)展中的一個(gè)隱患。發(fā)達(dá)經(jīng)濟(jì)體對(duì)住房抵押貸款的風(fēng)險(xiǎn)管理方式有以下兩種:一種是通過資產(chǎn)證券化手段將貸款包裝成證券化產(chǎn)品,如抵押資產(chǎn)支持證券,擔(dān)保債務(wù)憑證等并對(duì)外銷售,從而將風(fēng)險(xiǎn)轉(zhuǎn)移出去。另一種是購買相關(guān)金融產(chǎn)品如信用違約互換等進(jìn)行風(fēng)險(xiǎn)對(duì)沖。但由于我國(guó)缺乏相應(yīng)的創(chuàng)新工具,風(fēng)險(xiǎn)管理方式也僅僅止步于住房抵押覆蓋和借款人現(xiàn)狀審查。在當(dāng)前國(guó)內(nèi)大環(huán)境下,住房貸款違約一旦發(fā)生,由此產(chǎn)生的資金及信用損失將幾乎全部由銀行和地方政府承擔(dān),嚴(yán)重?fù)p害了社會(huì)的穩(wěn)定和城市的可持續(xù)發(fā)展。
一、文獻(xiàn)回顧
房地產(chǎn)市場(chǎng)對(duì)城市發(fā)展的作用毋庸置疑,眾多學(xué)者從經(jīng)濟(jì)理論和統(tǒng)計(jì)分析等角度論證了房地產(chǎn)經(jīng)濟(jì)的合理增長(zhǎng)對(duì)城市經(jīng)濟(jì)增長(zhǎng)具有重要意義,同時(shí)指出,過快或過慢都會(huì)影響城市發(fā)展的穩(wěn)定增長(zhǎng)[1]。泡沫化的過快增長(zhǎng)會(huì)對(duì)城市化進(jìn)程產(chǎn)生嚴(yán)重的負(fù)面效果,而房地產(chǎn)市場(chǎng)失速帶來的違約風(fēng)險(xiǎn)同樣會(huì)造成金融體系的不穩(wěn)定[2]。
國(guó)外學(xué)者很早就開始關(guān)注影響住房抵押貸款違約的各類因素,隨著期權(quán)的應(yīng)用和推廣,從期權(quán)定價(jià)理論的角度對(duì)住房抵押貸款進(jìn)行相應(yīng)的定價(jià)工作也成為了一個(gè)主要研究方向。Kau等[3]以及Kau和Keenan[4]在考慮提前償付和違約風(fēng)險(xiǎn)的基礎(chǔ)上分別從固定利率和浮動(dòng)利率的假設(shè)出發(fā),對(duì)住房抵押貸款的定價(jià)問題做了相應(yīng)的研究。另外,隨著住房抵押貸款證券化產(chǎn)品的普及,也有相當(dāng)一部分研究討論了相關(guān)證券化產(chǎn)品(如MBS)的定價(jià)問題。Schwartz和Torous[5]通過估計(jì)借款者每一期提前支付的概率分布函數(shù)研究了MBS的定價(jià)問題。Stanton[6]給出了借款者關(guān)于提前償付的理性決策模型,并以此為基礎(chǔ)對(duì)MBS進(jìn)行定價(jià)。
國(guó)內(nèi)學(xué)者在這方面的研究還相對(duì)較少。唐文進(jìn)和陳勇[7]利用期權(quán)定價(jià)的方法給出了住房抵押貸款的定價(jià)結(jié)果,同時(shí)討論了利率水平、房?jī)r(jià)水平與貸款的提前償還和違約可能性的關(guān)系。魏成龍和王述評(píng)[8]對(duì)于國(guó)內(nèi)住房抵押貸款的提前償付率進(jìn)行了相應(yīng)的實(shí)證研究。龔瀟瀟等[9]在考慮住房投資需求的基礎(chǔ)上研究了住房抵押貸款的定價(jià)問題。
本文基于國(guó)內(nèi)外學(xué)者的研究,從期權(quán)角度出發(fā),利用我國(guó)房地產(chǎn)市場(chǎng)的數(shù)據(jù),針對(duì)止贖房產(chǎn)處置問題進(jìn)行的相關(guān)研究具有實(shí)際意義和廣泛的應(yīng)用空間。
二、模型構(gòu)建
我們首先構(gòu)建市場(chǎng)模型,該模型可以用于描述抵押資產(chǎn)以及與抵押資產(chǎn)相關(guān)的資產(chǎn)價(jià)格行為。假設(shè)市場(chǎng)中的無風(fēng)險(xiǎn)收益率為r,同時(shí)存在一類抵押資產(chǎn)和兩類金融資產(chǎn)。對(duì)于這三類資產(chǎn)我們分別做如下假設(shè):
(一)抵押資產(chǎn)
用隨機(jī)過程{Pt}表示抵押資產(chǎn)價(jià)格,并且假設(shè){Pt}服從下面的伊藤過程:
dPt/Pt= μ(Pt,t)dt+σ(Pt,t)dWt
(1)
其中,μ(Pt,t)為漂移率,σ(Pt,t)為波動(dòng)率,Wt為標(biāo)準(zhǔn)布朗運(yùn)動(dòng)。
抵押資產(chǎn)可以是各種類型的資產(chǎn),如商品房、股票和債券等。
(二)金融資產(chǎn)Ⅰ
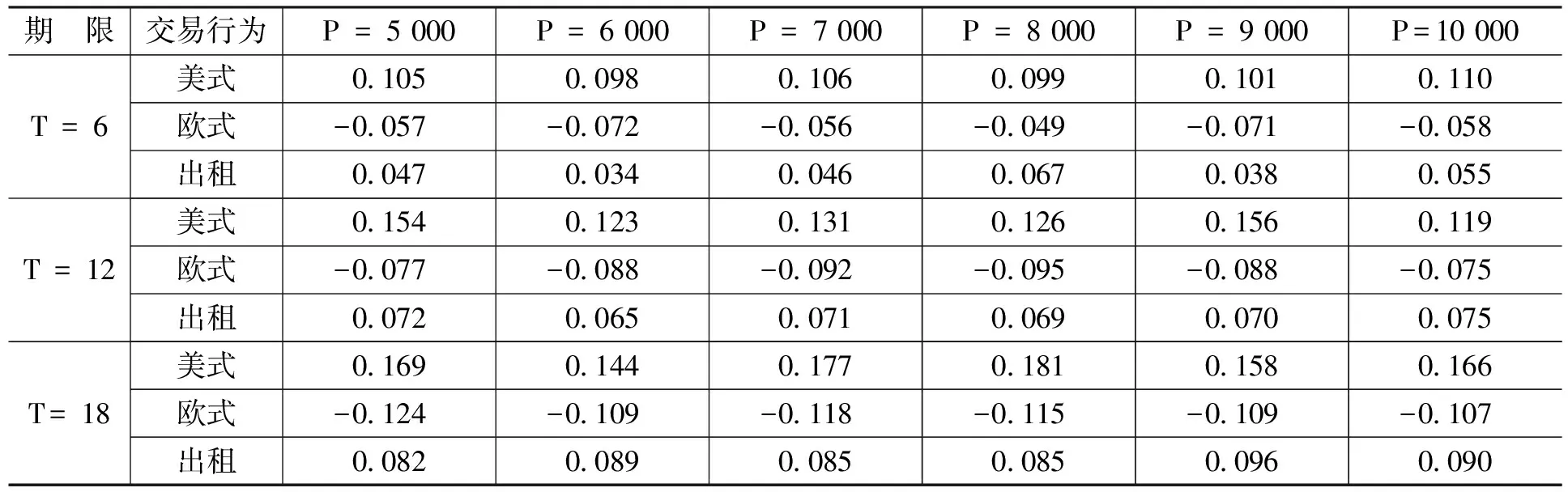
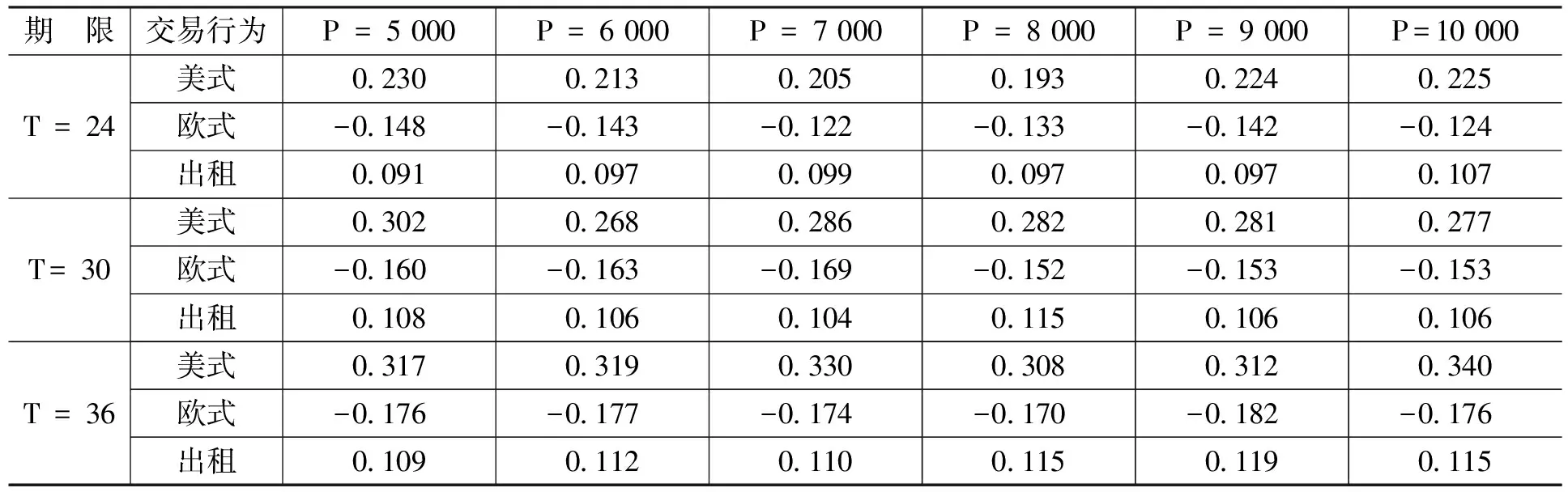
金融資產(chǎn)Ⅰ是關(guān)于抵押資產(chǎn)的抵押合同,合約期限為N。合約內(nèi)容規(guī)定,從初始時(shí)刻0到合約到期時(shí)刻N(yùn)之間共有n個(gè)交易日,即0=t0 金融資產(chǎn)Ⅱ是有條件抵押資產(chǎn)處置合約,合約期限與抵押貸款合同有效期相同。合約規(guī)定,當(dāng)金融資產(chǎn)Ⅰ發(fā)生違約的條件滿足時(shí),金融資產(chǎn)Ⅱ的合同將開始執(zhí)行,合同持有者將按照約定的價(jià)格購買或者租用抵押資產(chǎn),其中,買賣或者租用的選擇權(quán)屬于合約對(duì)手方(商業(yè)銀行)。 我們不難發(fā)現(xiàn),金融資產(chǎn)Ⅱ的租用條款實(shí)際上是附帶租賃服務(wù)的以抵押資產(chǎn)為標(biāo)的的美式看漲期權(quán):租賃期限T為行權(quán)期,租賃期內(nèi)的約定購買價(jià)格K=Pt·er(τ-t)為行權(quán)價(jià)(我們假設(shè)以無風(fēng)險(xiǎn)收益率作為連續(xù)復(fù)利率計(jì)算得到的價(jià)格為銀行可接受的最低行權(quán)價(jià)),合約對(duì)手方為獲得權(quán)利而繳納的費(fèi)用C為期權(quán)費(fèi)。 根據(jù)金融資產(chǎn)Ⅰ的理性違約假設(shè),當(dāng)金融資產(chǎn)Ⅰ發(fā)生違約時(shí),有Pt 當(dāng)然,除執(zhí)行金融資產(chǎn)Ⅱ的合同外,商業(yè)銀行也可以選擇其他傳統(tǒng)的抵押資產(chǎn)處置方式,如直接將抵押資產(chǎn)以違約時(shí)的市價(jià)Pt在市場(chǎng)中出售變現(xiàn);或者將抵押資產(chǎn)出租,并且在租期結(jié)束后再以當(dāng)時(shí)市價(jià)Pt+T對(duì)其進(jìn)行處置的方法等。 相比這些傳統(tǒng)方法,金融資產(chǎn)Ⅱ?yàn)樯虡I(yè)銀行處置貸款的抵押資產(chǎn)提供了一種新的選擇:利用金融資產(chǎn)Ⅱ,當(dāng)?shù)盅嘿J款(金融資產(chǎn)Ⅰ)發(fā)生違約時(shí),商業(yè)銀行可以通過提供抵押資產(chǎn)的租賃服務(wù)并收取租金,保持自身的流動(dòng)性和資本充足率;同時(shí)由于銀行實(shí)際持有抵押資產(chǎn),因此,在抵押資產(chǎn)價(jià)格上漲時(shí),銀行也可以從中獲得收益。此外,標(biāo)的資產(chǎn)多頭與看漲期權(quán)空頭組成的拋補(bǔ)看漲期權(quán)組合能夠降低銀行在未來所得收益的波動(dòng)。 根據(jù)傳統(tǒng)期權(quán)定價(jià)理論,在標(biāo)的資產(chǎn)價(jià)格服從幾何布朗運(yùn)動(dòng)以及其它一些假設(shè)條件下,看漲期權(quán)的價(jià)格C可以由下列偏微分方程給出: ?C/?t+(1/2) σ2P2(?2C/?P2)+rP(?C/?P)-rC=0 (2) 其中,P為標(biāo)的資產(chǎn)價(jià)格,r為無風(fēng)險(xiǎn)收益率,σ為標(biāo)的資產(chǎn)收益率的波動(dòng)率。 在歐式期權(quán)行權(quán)時(shí)間確定的約束下(τ=T),我們有初始條件C=max{PT-K,0}·e-rT,進(jìn)一步地,上述偏微分方程可以得到相應(yīng)的解析解;而在美式期權(quán)結(jié)構(gòu)行權(quán)時(shí)間不確定的情況下,初始條件C=max{Pτ-K,0}·e-rτ中的停時(shí)τ不是一個(gè)定值,因而很難得到解析形式的解。另外,在價(jià)格路徑不服從幾何布朗運(yùn)動(dòng)的條件下,上述偏微分方程也需要做相應(yīng)修正。因此,關(guān)于美式期權(quán)定價(jià)問題的研究在絕大多數(shù)情況下均是通過數(shù)值模擬方法求出其數(shù)值解。 假設(shè)某美式期權(quán)的行權(quán)期限為T,除初始時(shí)刻外,行權(quán)期內(nèi)有m個(gè)交易日(0=t0 (1)找出tm=T時(shí)刻(最后一個(gè)時(shí)點(diǎn))期權(quán)處于實(shí)值狀態(tài)的價(jià)格路徑,并標(biāo)記為可能的行權(quán)時(shí)點(diǎn)(如果處于虛值狀態(tài)顯然不會(huì)行權(quán))。 (2)找出tm-1時(shí)刻期權(quán)處于實(shí)值狀態(tài)的價(jià)格路徑,并將相應(yīng)路徑上未來時(shí)刻(此時(shí)為tm時(shí)刻)的現(xiàn)金流貼現(xiàn)到當(dāng)前時(shí)點(diǎn)(以美式看漲期權(quán)為例,假設(shè)第k條價(jià)格路徑的tm時(shí)刻在第(1)步中被標(biāo)記為行權(quán)時(shí)點(diǎn),則貼現(xiàn)現(xiàn)金流為(K-PkT)·e-r(tm-tm-1);否則貼現(xiàn)現(xiàn)金流為0),并將貼現(xiàn)現(xiàn)金流作為被解釋變量,將當(dāng)前時(shí)點(diǎn)的標(biāo)的資產(chǎn)價(jià)格和與之相關(guān)的其他變量(如價(jià)格的平方項(xiàng)、三次方項(xiàng)等)作為解釋變量進(jìn)行回歸,得到回歸系數(shù)的估計(jì)。 (3)將選取的解釋變量代入回歸方程中,得到在當(dāng)前時(shí)點(diǎn)可得信息集的基礎(chǔ)上未來貼現(xiàn)現(xiàn)金流的條件期望。 (4)將當(dāng)前時(shí)點(diǎn)立即行權(quán)可得的現(xiàn)金流與未來貼現(xiàn)現(xiàn)金流的條件期望進(jìn)行比較,若當(dāng)前時(shí)點(diǎn)的現(xiàn)金流更大,則記當(dāng)前時(shí)點(diǎn)為新的行權(quán)時(shí)點(diǎn),否則不在當(dāng)前時(shí)點(diǎn)行權(quán)。 (5)從tm-2時(shí)刻起往前的每一個(gè)時(shí)刻,依次重復(fù)上述(2)—(4)的步驟,直到t1時(shí)刻為止,得到每條路徑可能的行權(quán)時(shí)點(diǎn)。 (6)將每條路徑的期望現(xiàn)金流貼現(xiàn)到初始時(shí)刻并取均值,即可得到相應(yīng)期權(quán)的模擬定價(jià)結(jié)果。 另外,需要特別指出的一點(diǎn)是:通常認(rèn)為,美式看漲期權(quán)在完美的市場(chǎng)條件下不會(huì)提前行權(quán),因此其定價(jià)結(jié)果應(yīng)該與歐式看漲期權(quán)一致。但是針對(duì)本文所設(shè)計(jì)的以抵押資產(chǎn)為標(biāo)的的美式看漲期權(quán),顯然不存在與之對(duì)應(yīng)的流通性較強(qiáng)的二級(jí)市場(chǎng)等條件,因此,從數(shù)值模擬角度討論其提前行權(quán)的可能性和區(qū)別于歐式看漲期權(quán)的定價(jià)結(jié)果仍然具有實(shí)際意義。 本文的數(shù)據(jù)是2000—2016年國(guó)內(nèi)商品房平均銷售價(jià)格月度數(shù)據(jù),單位為元/平方米,數(shù)據(jù)來源為中國(guó)房地產(chǎn)信息網(wǎng)。 我們先設(shè)定一組參數(shù):無風(fēng)險(xiǎn)收益率r=5%。抵押資產(chǎn)初始價(jià)格與月租金比值rRP=200。對(duì)抵押資產(chǎn)的價(jià)格路徑{Pt},在幾何布朗運(yùn)動(dòng)的假設(shè)條件下進(jìn)行模擬,模擬通過MATLAB軟件編程實(shí)現(xiàn),每種情況下的模擬路徑均為10 000條。模型形式如下: dPt/Pt=μdt+σdWt (3) 幾何布朗運(yùn)動(dòng)中的參數(shù)取值為:μ=0.073,σ=0.360。 表1和表2給出了不同合約期限T(單位為月,下同)和止贖房產(chǎn)初始價(jià)格P(單位為元/平方米,下同)下以抵押資產(chǎn)為標(biāo)的的美式和歐式看漲期權(quán)的模擬價(jià)格。 從表1和表2可以看出,隨合約期限的延長(zhǎng)和初始價(jià)格的上升,兩類期權(quán)價(jià)格均呈現(xiàn)出上升的趨勢(shì)。另外,由于在行權(quán)時(shí)間方面有較高的自由度,美式期權(quán)的價(jià)格普遍高于歐式期權(quán)。 表1 美式期權(quán)合約模擬價(jià)格 單位:元/平方米 資料來源:中國(guó)房地產(chǎn)信息網(wǎng),下同。 表2 歐式期權(quán)合約模擬價(jià)格 單位:元/平方米 在已經(jīng)得到的美式和歐式看漲期權(quán)價(jià)格的基礎(chǔ)上,表3展示了在不同的合約期限T和抵押資產(chǎn)初始價(jià)格P的條件下,商業(yè)銀行出售以抵押資產(chǎn)為標(biāo)的的美式期權(quán),出售以抵押資產(chǎn)為標(biāo)的的歐式期權(quán)和出租抵押資產(chǎn)這三種交易行為的收益情況。三種交易行為下的收益均從行權(quán)時(shí)點(diǎn)起以無風(fēng)險(xiǎn)收益率r = 5%為貼現(xiàn)率貼現(xiàn)到初期,以便與初始價(jià)格P進(jìn)行比較。 表3 三種交易行為的貼現(xiàn)期望收益 單位:元/平方米 從表3的模擬結(jié)果中可以看出:美式期權(quán)可能被提前行權(quán)的時(shí)間價(jià)值,以及高于歐式期權(quán)的期權(quán)費(fèi)使得出售美式期權(quán)的收益明顯高于出售歐式期權(quán);由于模擬價(jià)格路徑的參數(shù)都是從實(shí)際數(shù)據(jù)(2000—2016年國(guó)內(nèi)商品房平均銷售價(jià)格月度數(shù)據(jù))中估計(jì)得到的,而在此期間國(guó)內(nèi)住房?jī)r(jià)格呈持續(xù)上升的趨勢(shì),因此,價(jià)格路徑中的漂移率μ相對(duì)較高,導(dǎo)致合約到期時(shí)的止贖房產(chǎn)價(jià)格Pt+T有較大概率高于以無風(fēng)險(xiǎn)收益率r作為連續(xù)復(fù)利率時(shí)的商業(yè)銀行最低可接受行權(quán)價(jià)K=PterT,從而使得出租抵押資產(chǎn)的收益高于出售歐式期權(quán);此外,三種交易行為所得的貼現(xiàn)收益均高于初始價(jià)格,說明這三種交易行為均優(yōu)于在收回抵押資產(chǎn)當(dāng)期直接將其拋售的處理方法。 表4則比較了三種交易行為的Sharpe比率。從表4可以看出,由于出售美式期權(quán)的收益高于出售歐式期權(quán),同時(shí)收益的波動(dòng)差別不大,因此,出售美式期權(quán)時(shí)資產(chǎn)組合的Sharpe比率明顯高于出售歐式期權(quán)時(shí)的情況;看漲期權(quán)空頭和標(biāo)的資產(chǎn)多頭形成的拋補(bǔ)看漲期權(quán)組合顯著降低了收益的波動(dòng),因而盡管出售歐式期權(quán)的收益低于直接出租止贖房產(chǎn),但是出售歐式期權(quán)的Sharpe比率仍然高于出租止贖房產(chǎn)。另外,由于在參數(shù)設(shè)定中將抵押資產(chǎn)價(jià)格與月租金的比值rRP取為200,導(dǎo)致租金的收益率(6%)高于無風(fēng)險(xiǎn)收益率(5%),因此,隨著合約期限的延長(zhǎng),三種交易行為的Sharpe比率都呈現(xiàn)出明顯的上升趨勢(shì)。 表4 三種交易行為的Sharpe比率 由于租金可能導(dǎo)致較長(zhǎng)期限合約的Sharpe比率偏高,并且對(duì)三種交易行為而言都是一致的,因此,表5給出了忽略租金這一因素后三種交易行為的Sharpe比率模擬結(jié)果。 表5 三種交易行為的Sharpe比率(不考慮租金) 續(xù)表 從表5可以看出,出售美式期權(quán)所得收益更低的波動(dòng)導(dǎo)致了更高的Sharpe比率;歐式期權(quán)的Sharpe比率絕對(duì)值大于出租抵押資產(chǎn)的Sharpe比率,表明出售期權(quán)所得收益的波動(dòng)明顯小于出租抵押資產(chǎn),證明了此種金融創(chuàng)新工具的使用可以有效降低房地產(chǎn)市場(chǎng)的不穩(wěn)定。 首先,期權(quán)的模式使得銀行不僅不需要放棄止贖房產(chǎn)價(jià)值的上漲空間,相反還可以通過設(shè)定合適的行權(quán)價(jià),確保自身在房?jī)r(jià)上升過程中也能得到一定的收益。 其次,銀行在出售以止贖房產(chǎn)為標(biāo)的的看漲期權(quán)后,看漲期權(quán)空頭與自身持有的止贖房產(chǎn)多頭構(gòu)成了拋補(bǔ)看漲期權(quán)組合,能夠有效降低資產(chǎn)組合收益的波動(dòng)。因此,對(duì)于銀行而言,出售以止贖房產(chǎn)為標(biāo)的、同時(shí)附帶出租條款的期權(quán)結(jié)構(gòu)證券在收益波動(dòng)率和Sharpe比率等方面的表現(xiàn)要顯著優(yōu)于直接將止贖房產(chǎn)出租的方法,能夠保證銀行得到更加穩(wěn)定的收益。 最后,在某些特殊時(shí)期,將止贖房產(chǎn)作為看漲期權(quán)的標(biāo)的資產(chǎn)出售同樣可以緩解銀行面臨的止贖壓力。銀行不直接出售止贖房產(chǎn)可以對(duì)房?jī)r(jià)的下跌趨勢(shì)形成緩沖,有助于維持市場(chǎng)的穩(wěn)定。因此,本文設(shè)計(jì)的這種創(chuàng)新金融工具可以有效降低房地產(chǎn)市場(chǎng)不穩(wěn)定對(duì)城市發(fā)展帶來的負(fù)面影響。(三)金融資產(chǎn)Ⅱ
三、數(shù)值模擬方法
四、數(shù)據(jù)來源和模擬分析
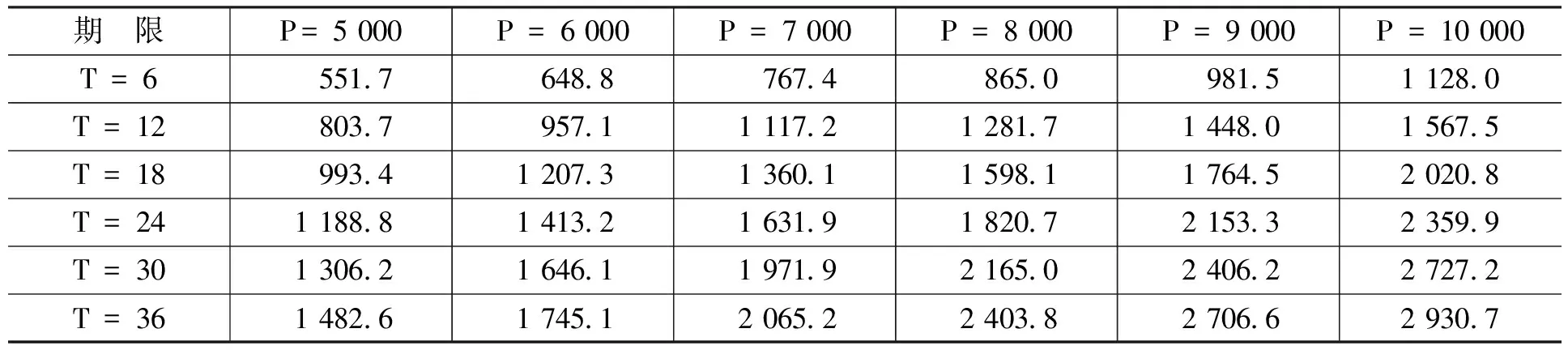
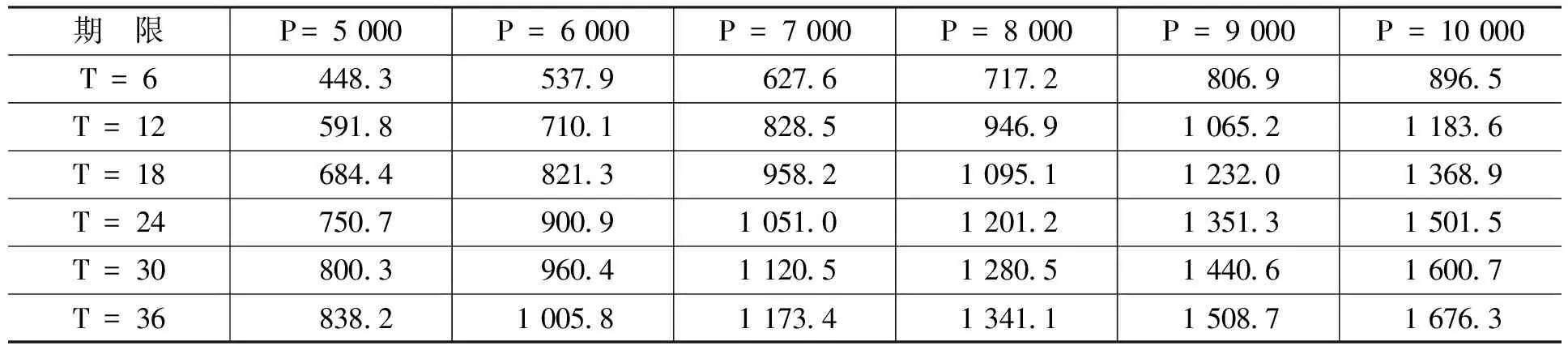
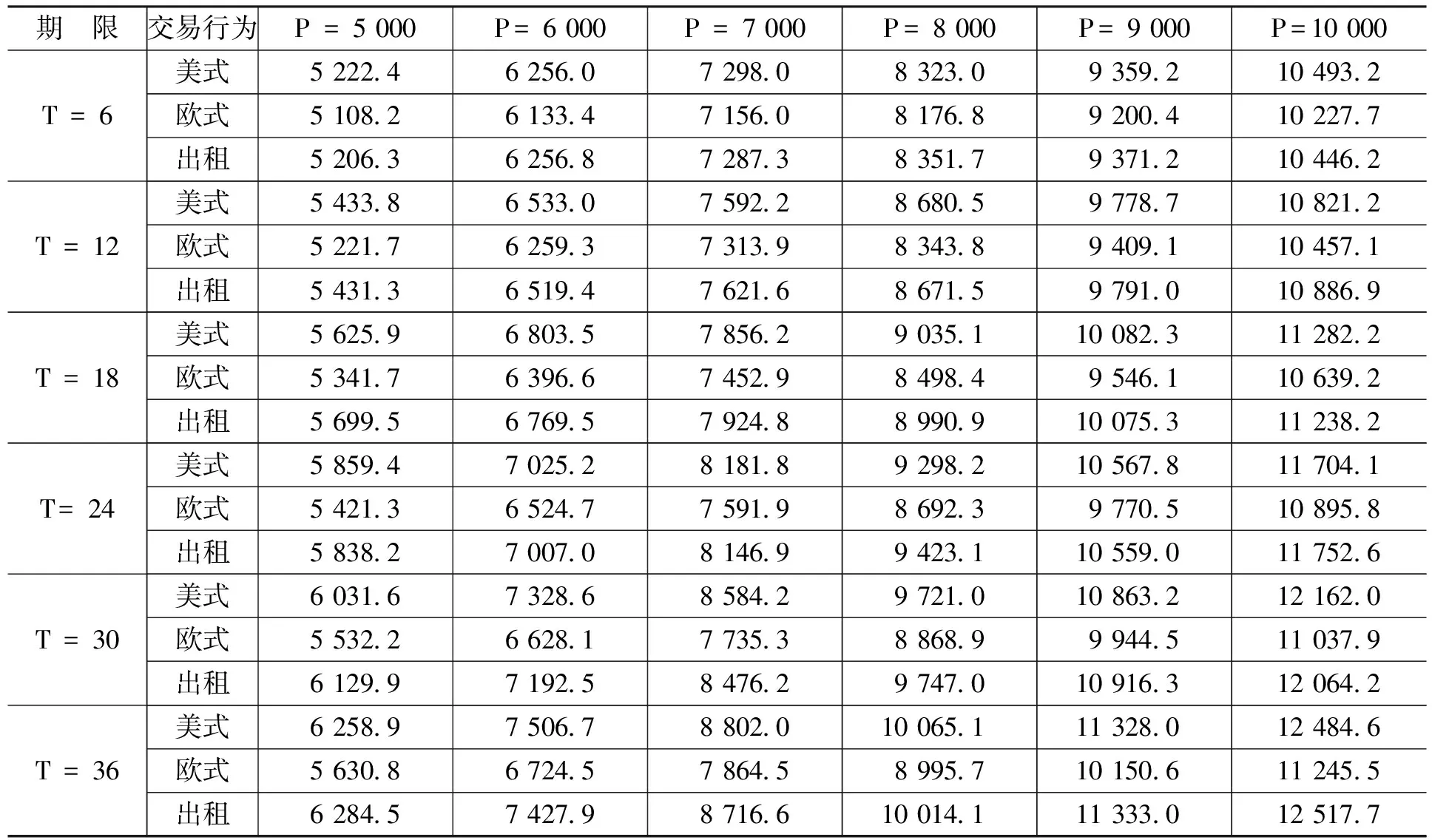
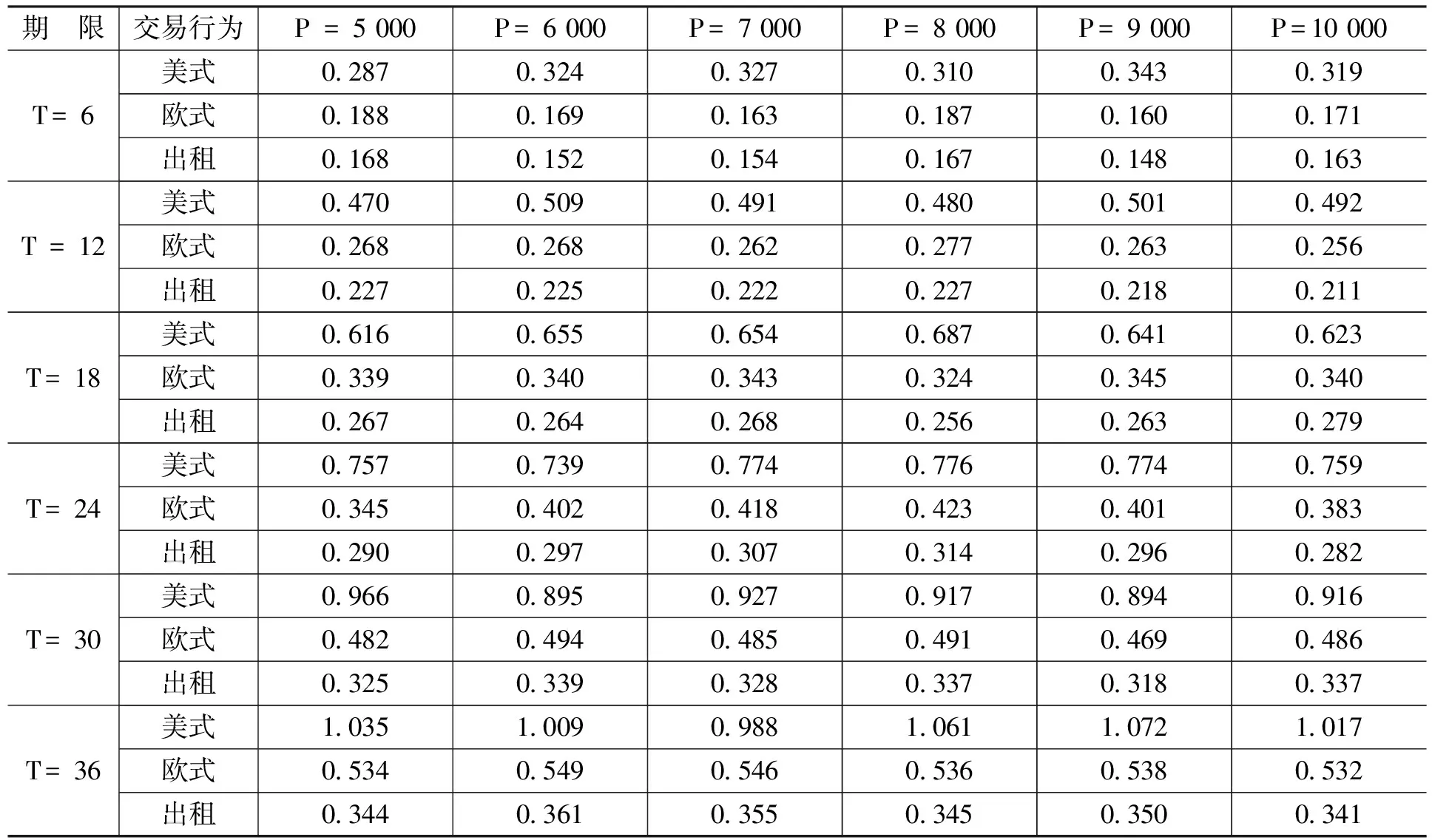
五、結(jié) 論

