基于模糊聚類排序及狀態均勻性的電網安全性風險評估
黃文婧,李華強,楊植雅,余雪瑩
(四川大學 電氣信息學院, 成都 610065)
0 引 言
近年來,世界各地常有大停電事故的發生[1]。通過對多起大停電事故分析發現[2-4],辨識出對系統危害較大的初始故障集合及已知連鎖故障序列中的關鍵環節,并采取相應控制措施,可以最大程度上防止大停電事故的發生。因此全面合理地評估事故后系統嚴重性,對減少大停電事故的發生具有實際意義。
風險評估[5]是同時考慮事故發生可能性和嚴重性的評估方法,廣泛應用于電網安全評估中。文獻[6-7]從系統的不確定性出發,建立具有模糊故障率和模糊嚴重度模型的風險評估模型。文獻[8-9]計及各指標重要度的差異性,使用層次分析法求取指標權重,并建立綜合嚴重度模型。在此基礎上,文獻[10]考慮電網運行狀態對指標權重的影響,建立變權重機制下的綜合嚴重度模型。
上述文獻在建立綜合嚴重度模型時,忽略了系統狀態均勻性對嚴重度的影響,并均采用各指標歸一化后的嚴重度或隸屬度加權求和的方法,求取系統綜合嚴重度。目前加權求和方法眾多也相對成熟,但均存在如下缺點: 即使歸一化處理數據,不同指標的同值數據代表的嚴重度不同,各指標數據不具可比性,不宜加權求和;綜合嚴重度指標物理意義不明確,以此為依據的嚴重度排序,可理解性、準確性較差。為此,提出基于模糊聚類排序算法,并充分考慮系統狀態均勻性的安全性風險評估方法。首先,依據運行可靠性理論,建立電網故障概率模型;其次,基于熵理論,建立狀態分布熵指標,并引入嚴重度模型。然后,從“物以類聚”思想出發,使用模糊聚類排序算法,求取事故嚴重度。最后,采用IEEE30節點系統仿真,對N-1故障風險大小排序,對N-k故障逐級風險評估,并與現有方法對比分析。
1 電網故障概率模型
輸電線路故障率,不僅與其壽命、自身健康狀況、天氣狀態等因素有關,還與線路負載率相關。當輸電線路負載率較高時,其故障概率也隨之上升。因此,從運行可靠性理論出發,考慮系統運行狀態對線路故障率的影響,建立基于潮流變化的支路故障概率模型[11]:
(1)

N-k故障概率采用文獻[12]的條件概率模型:
P(Ei)=P(Ei-1)P(Ei|Ei-1),i>1
(2)
式中P(Ei∣Ei-1)為第i-1故障發生情況下,第i級故障發生的概率。
2 基于模糊聚類排序的事故嚴重度模型
潮流過載、電壓降低和負荷丟失為電力系統故障后的典型表現[13]。因此,從以上三個方面,并充分考慮系統的均勻性,建立事故嚴重度模型。
2.1 系統狀態分布熵
由文獻[14-15]可知,電網狀態(即潮流、電壓、負荷)分布越均勻,系統存在明顯薄弱環節的可能性越小。從而,系統抵抗各類不確定性事件的能力越強,其安全程度越高。因此,從熵理論出發,建立狀態分布熵指標,以修正各指標的嚴重度值。
2.1.1 潮流分布熵
(3)
(4)

(5)

2.1.2 電壓分布熵
(6)
(7)

(8)
式中υi為節點i的電壓率;Ui為節點i的實際電壓;Un為節點i的額定電壓;M為節點數;vk為處于電壓比率第k區間的節點數;D(k)為第k區間的節點數占節點總數的比例;H(V)為電壓分布熵,其值越大,各節點電壓值越不均勻。
2.1.3 負荷分布熵
(9)
(10)

(11)
式中ζi為負荷i的負荷率;Si為負荷i的負荷量;Stotal為系統負荷總量;G為負荷數;sk為處于負荷率第k區間的負荷數;F(k)為第k區間的負荷數占負荷總數的比例;H(S)為負荷分布熵,其值越大,系統負荷分布越不均勻。
2.2 事故嚴重度模型
2.2.1 線路過載嚴重度指標
對于線路l,其線路過載嚴重度函數表示為:
(12)
式中Pl為線路當前有功功率;Pd為線路過載風險警戒閾值,一般取線路極限容量的90%;Plim為線路過載風險閾值,取線路極限容量值。
考慮潮流分布均勻性和支路重要度,建立全局線路潮流過載嚴重度指標:
(13)
式中N表示系統中所有線路的集合;W(l)為支路重要度因子,與該支路傳輸容量、電壓等級、供應負荷類型等因素有關。
2.2.2 節點低電壓嚴重度指標
對于節點n,其低電壓嚴重度函數表示為:
(14)
式中Un為節點當前電壓幅值;Ud為節點低電壓風險警戒閾值,即節點額定電壓值;Ulim為節點低電壓風險閾值,一般取節點額定電壓的90%。
考慮電壓分布均勻性和節點重要度,建立全局節點低電壓嚴重度指標:
(15)
式中M為系統節點總和;W(n)為節點重要度,與該節點傳輸容量、電壓等級、連接設備類型等因素有關。
2.2.3 失負荷嚴重度
安全評估中主要考慮三種失負荷類型[16]: 負荷節點因相應供電線路因故退出運行而脫網,形成孤立節點,此情況下負荷損失量為該節點的負荷量;負荷節點母線電壓低至低壓減載裝置設定值后,低壓減載裝置切除設定的負荷量;系統解列成若干個孤島后,為保持孤島功率平衡,加入相關控制措施后系統丟失的負荷量。計及負荷的重要度及其分布的均勻性,建立失負荷損失嚴重度函數。
(16)
(17)
式中η是系統負荷丟失率;L是負荷節點集合;L′是失負荷節點集合;εi為負荷節點i重要度因子;Plossi為節點i負荷丟失量;Pj為節點j事故前所帶負荷;Sload為失負荷嚴重度;ηlim為失負荷設定閾值,一般取電網總負荷的20%。
負荷重要度因子是負荷損失嚴重度模型的重要組成部分。我國根據電力負荷對供電可靠性的要求及其中斷后對政治、經濟上造成的損失,將其分為三個等級。在一個負荷節點下,負荷可能由這三種等級的負荷組成。因此,負荷重要度因子具體構成為:
(18)
式中Lloss1、Lloss2、Lloss3為節點i中一級負荷、二級負荷和三級負荷損失量;εi1、εi2、和εi3為一級、二級和三級負荷的重要度系數;Lloss為負荷損失總量。
2.3 基于模糊聚類排序的全局綜合嚴重度模型
模糊聚類[17]是一種根據客觀事物親疏程度,通過建立模糊相似關系對事物歸類的研究方法,鮮用于事件的排序。首先建立虛擬的最優和最差標準事件,接著求取待求事故與標準事件的相似系數,然后對相似系數修正,最后根據修正后的相似系數得到待求事故的綜合嚴重度值。文中方法與加權求和方法相比,能從客觀上體現該事故與最優事件及最差事件的全局相似性,所得結果物理意義明確,便于理解;無需將各指標相加,避免了指標可比性問題對結果的影響。其具體步驟如下:
(1)數據標準化。
(19)
(2)引入標準事件。
文中指標均為逆向指標。最優標準事件為xmin={x1min,x2min,…,xmmin},(i=1,2,…,m),由各指標最小值構成。最差標準事件為xmax={x1max,x2max,…,xmmax},由各指標最大值構成。
(3)構建模糊相似矩陣。
模糊相似矩陣R由各事件的模糊相似系數rij構成:
(20)
式中rij∈[0,1],值越大表明兩者相似性越高。
(4)相似系數的求取。
采用計及各指標權重ωk的加權歐式距離法,求取模糊相似系數:
(21)
(22)
rij=1-cd(xi,,xj)
(23)
(5)系統綜合嚴重度。
對事故嚴重度排序,基于與最優標準事件的相似系數排序結果,和與最差事件的相似系數排序結果有所出入。因此,為了減少誤差,采用式(24)修正。修正值可較準確反映事故i相對于最差標準事件的相似性,即可反映事故的嚴重程度。因此,可用此值代表事故綜合嚴重度值Si:
Si=rimax-rimin
(24)
3 安全性風險評估模型及流程
綜合考慮第i級故障的故障概率及故障后系統全局綜合嚴重度,建立第i級故障后系統安全性風險指標:
Ri=P(Ei)×Si
(25)
安全性風險評估流程圖如圖1所示。

圖1 風險評估流程Fig.1 Flow chart of risk assessment
4 算例分析
4.1 概述
采用IEEE30節點系統仿真,該系統含6臺發電機,41條線路。系統中全部節點采用單母線接線方式。仿真過程中線路主保護動作概率取0.85[18],誤動作概率取0.05[18]。采用文獻[10]方法求取元件重要度,系統連接圖如圖2所示。

圖2 IEEE30 系統接線圖Fig.2 Connection diagram of IEEE 30-bus system
4.2 N-1事故風險辨識
根據本文所提方法,考慮系統均勻性,對系統N-1故障的安全性風險進行分析。得到風險值前10的線路排序,并與采用文獻[10]所提方法的計算結果及傳統方法比較。其中傳統方法僅考慮了系統狀態嚴重度,并采用各指標直接相加的方法求取系統綜合嚴重度指標;文獻[10]考慮了元件重要的差異,并采用變權重機制的加權求和方法求取系統綜合嚴重度。
根據表1數據所示,文中方法得到的高風險支路集合,和文獻[10]及傳統方法結果有很多相似之處,特別是在對排名最靠前支路的風險值辨識。比如支路L1、L2,其與1號發電機直接相連,一旦故障,極有可能導致發電機與主網分離,系統解列運行。因此,該使用方法具有正確性和有效性。傳統方法對高風險事故的辨識較差,如傳統方法中支路L32、L7非系統關鍵外送、聯絡通道。這是因為傳統方法僅考慮了系統狀態嚴重度,并采取各指標直接相加的方式求取系統綜合嚴重度,沒有考慮元件及指標重要度之間的差異。文獻[10]辨識度相對較好,但支路L12、L11并非某區域負荷的唯一供電通道,故障造成的影響不及L35。并且沒有辨識出高風險支路L10、L6。這是因為該文獻沒有考慮系統的均勻性,且加權求和方法存在指標可比性問題。文中方法排序相對靠前的支路中,支路L10與發電機直接相連,向8號重負荷節點供電,傳輸任務較重,故障會導致支路L39潮流反向,支路L40負載率大幅度提升,嚴重威脅系統安全運行。L35是主干變壓器支路,具有很大的供電范圍,故障斷線,會使支路L30、L32過載,極可能導致系統右下側節點,即24~30節點與系統解列,引發系統大面積停電,極大程度破環系統潮流、電壓、負荷分布的均勻性。類似的還有支路L41、L6,均為發電機節點和中樞節點的連接支路,是系統功率的重要傳輸路徑,一旦故障,極可能引發系統連鎖故障、電壓崩潰。因此,該方法能很好的辨識具有高風險的初始故障。
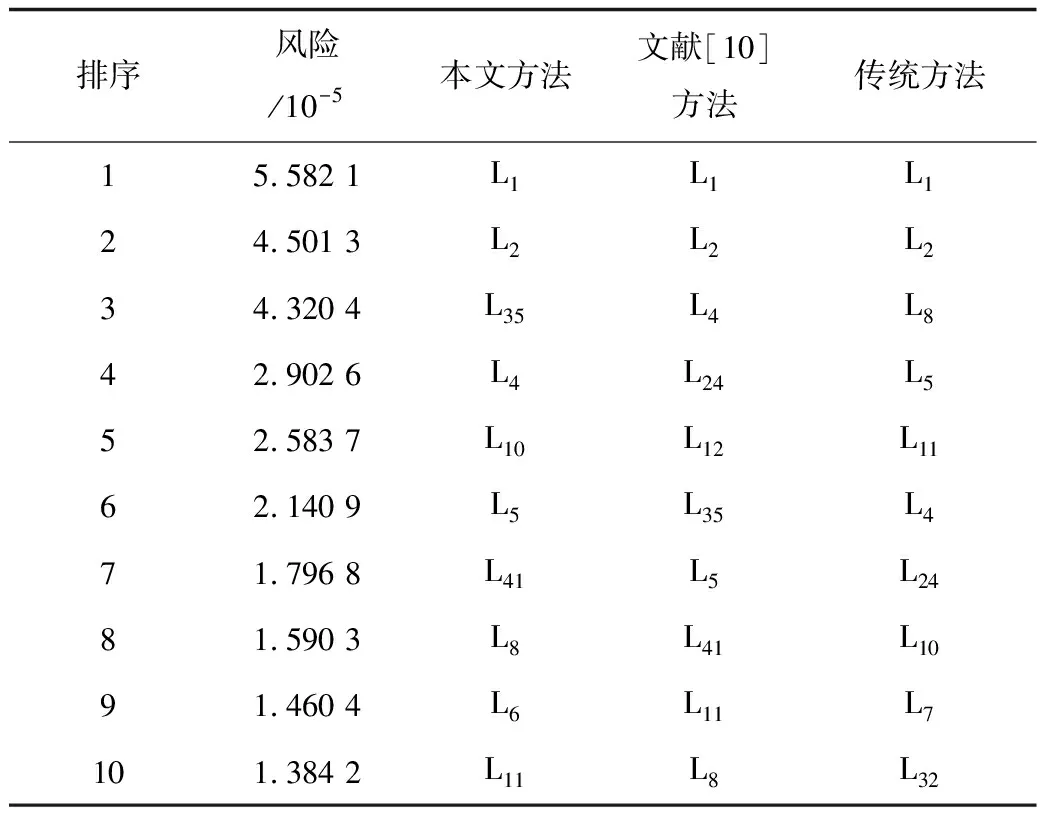
表1 N-1事故風險值前10排序Tab.1 Top 10 of N-1 contingency risk value
4.3 N-k事故關鍵環節辨識
根據前文所述N-k風險評估方法,對以L5為初始故障的故障序列L5-L6-L3-L2/L4進行逐級風險評估,并計算出每級的風險增量,從而辨識出N-k故障中的關鍵環節。
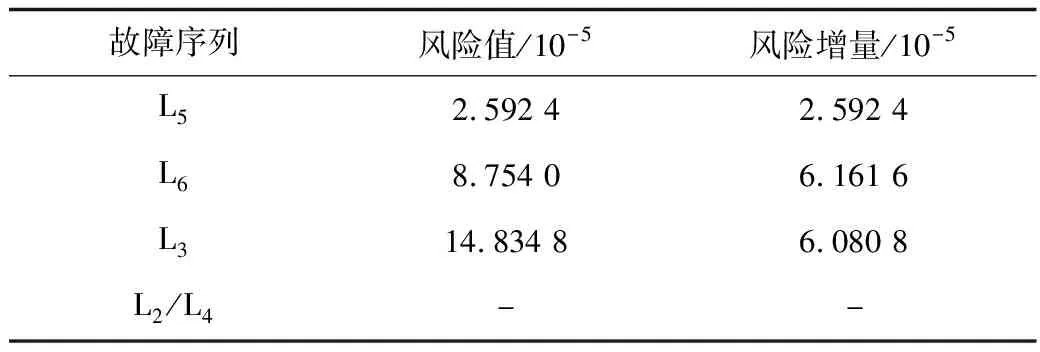
表2 L5為初始故障N-k故障序列關鍵環節辨識Tab.2 Critical link identification of N-k contingency series with initial fault of L5
*注: L2/L4故障后系統崩潰解列
由表2可以看出,支路L6故障后,系統風險急速增長,L3的故障則直接導致系統解列。說明支路L5、L6、L3為系統關鍵,L6、L3該故障序列的關鍵環節。經分析可知,上述三條線路為與2號發電機直接相連線路,傳輸任務繁重。此外,在電網拓撲結構上三條線路互為補充,任一條線路故障,另兩條線路都會出現不同程度的重載甚至過載,對系統造成嚴重影響。因此,提出的風險評估方法可以正確有效識別出N-k故障序列中的關鍵環節,并能較好地反映出連鎖故障中的風險變化趨勢。
5 結束語
提出一種基于模糊聚類排序的安全性風險評估方法。該方法計及系統狀態的均勻性,將狀態分布熵指標引入嚴重度模型。考慮嚴重度指標可比性、可理解性問題,使用模糊聚類排序求取綜合嚴重度模型。該方法評估結果符合實際情況,能正確有效識別出初始故障集中高風險集合及連鎖故障的關鍵環節,對提高電網的安全性具有實際意義。

