強賦值幺半群上的加權Mealy機與加權Moore機的關系*
王 敏,李永明
陜西師范大學 計算機科學學院,西安 710119
1 引言
加權自動機[1-6]是對經典自動機[7-8]的推廣,是轉移上附加權重的自動機。這些權重作成的代數結構通常是半環,Droste教授等在文獻[3]中已經很好地研究了取值于半環的加權有窮自動機的理論及其實際應用。2011年Droste教授在文獻[4]中首次提出賦值幺半群的概念,將半環推廣到更一般的賦值幺半群上,并在文獻[5]中對取值于賦值幺半群的加權自動機和加權單體二階邏輯進行詳細的闡述。對一個輸入字符串,不帶輸出的有窮自動機只判定此串是或者不是句子,這在許多時候是不夠的,原因是有時不僅希望系統能得出一個輸入串是否為要求串的結論,更希望系統在處理此串的過程中給出系統的輸出結果。Moore機和Mealy機就是兩種不同的帶有輸出的有窮自動機[7]。并且由于帶輸出的加權有窮自動機是自動機理論的一個重要研究方向,在自然語言的處理方面[9-11]有著很重要的意義。文獻[12]和文獻[13]分別在格序幺半群和分配格意義下,證明了格值序列機與格值Moore機是等價的,格值序列機與格值Mealy機是不等價的(包括格序幺半群取{0,1}時的情況)。從而得到了格值Mealy機與格值Moore機是不等價的。但格值序列機與格值Moore機的等價性成立是依賴于分配律的。文獻[14]和文獻[15]在強雙半群-偽半環意義下研究偽加權序列機、偽加權Mealy機以及偽加權Moore機的關系,得到了類似的結論,且結論成立不依賴于分配律,但偽半環和格序幺半群都滿足結合律。
本文在賦值幺半群的基礎上引入了新的概念—強賦值幺半群,并研究了取值于新的代數結構的強賦值加權序列機、強賦值加權Mealy機以及強賦值加權Moore機的關系,證明了強賦值加權序列機與強賦值加權Moore機是等價的,強賦值加權序列機與強賦值加權Mealy機是不等價的,從而得到了強賦值加權Mealy機與強賦值加權Moore機是不等價的,且上述結論成立既不依賴于分配律,強賦值幺半群也不需要滿足結合律。
2 預備知識
為了便于本文閱讀,現將與本文相關的概念介紹如下。
定義1[7]Mealy機是一個六元組:

其中,Q表示狀態的非空有窮集合;Σ表示輸入字母表;Δ表示輸出字母表;δ表示狀態轉移函數,有時又叫作狀態轉換函數或者移動函數,δ:Q×Σ→Q。?(q,a)∈Q×Σ,δ(q,a)=p表示M在狀態q讀入字符a,將狀態變成p,并將讀頭向右移動一個帶方格而指向輸入字符串的下一個字符;λ表示輸出函數,λ:Q×Σ→Δ。?(q,a)∈Q×Σ,λ(q,a)=d表示M在狀態q讀入字符a時輸出d;q0表示M的開始狀態,也可叫作初始狀態或者啟動狀態,q0∈Q。
顯然,?a1a2…an∈Σ?,M的輸出串為:λ(q0,a1)λ(δ(q0,a1),a2)…λ(δ(…δ(δ(q0,a1),a2)…),an), 設δ(q0,a1)=q1,δ(q1,a2)=q2,…,δ(qn-1,an)=qn,則M的輸出可以表示成λ(q0,a1)λ(q1,a2)…λ(qn-1,an),這是一個長度為n的串。
定義2[7]Moore機是一個六元組:
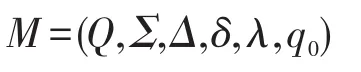
其中,Q,Σ,Δ,δ,q0的意義同Mealy機。λ表示輸出函數,λ:Q→Δ。?q∈Q,λ(q)=a表示M在狀態q時輸出a。
顯然,?a1a2…an∈Σ?,M的輸出串為:λ(q0)λ(δ(q0,a1))…λ(δ((…δ(δ(q0,a1),a2)…),an)),設δ(q0,a1)=q1,δ(q1,a2)=q2,…,δ(qn-1,an)=qn,則M的輸出可以表示成λ(q0)λ(q1)λ(q2)…λ(qn),這是一個長度為n+1的串。
定義3[4]設D是一個非空集合,(D,+,0)是一個可交換的幺半群,定義D上的賦值函數val:D+→D,若賦值函數滿足:
(1)?d∈D,val(d)=d;
(2)若存在i∈{1,2,…,n},使得di=0,則val(d1,d2,…,dn)=0 。
則稱D為賦值幺半群,記為(D,+,val,0)。
文中出現的∨與max表示相同意義,N表示自然數集,R表示實數集,并且用ε表示空字符串。
3 強賦值幺半群
定義4設D是一個非空集合,(D,+,val,0)是一個賦值幺半群,若賦值函數val:D+→D滿足,對任意自然數k:
(1)val作用于2k個元時,
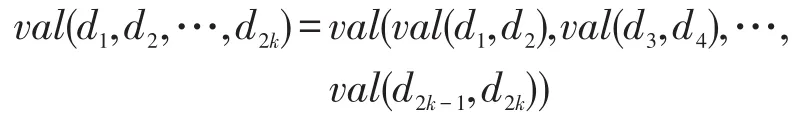
(2)val作用于2k+1個元時,

(3)存在元素e∈D,使得val(d,e)=d,?d∈D。
則稱D為強賦值幺半群,記為(D,+,val,0,e)。
例1以下代數結構為強賦值幺半群,并且賦值函數val滿足結合律。
(1)D=(?,+,×,0,1),D=(R,+,×,0,1)。
(2)D=(R+?{∞},+,∧,0,∞),其中R+={a∈R|a≥ 0}。
注1強賦值幺半群是偽半環的推廣,同時也是格序幺半群的推廣。進而,本文的結果可以看作文獻[12]和文獻[14]的進一步推廣。
通過下面的例子來說明強賦值幺半群比偽半環與格序幺半群條件弱。
例2設D=([0,1],max,val,0,1),賦值函數val定義如下:?x1,x2,…,xi∈[0,1],i∈N :

可以驗證D=([0,1],max,val,0,1)是強賦值幺半群,但賦值函數val不滿足結合律。
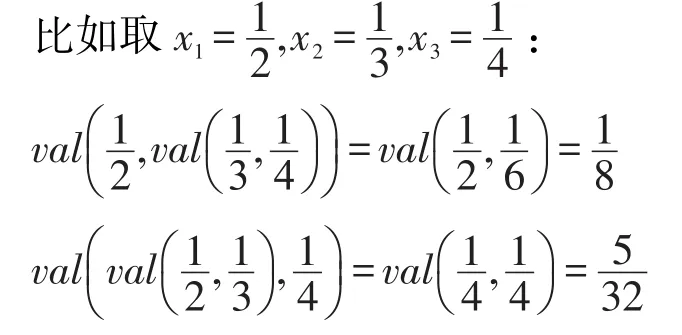
4 強賦值加權Mealy機與強賦值加權Moore機及其響應函數
定義5一個強賦值加權序列機是一個五元組M=(X,U,Y,f,I),其中,X為非空有限狀態集合;U為有限輸入字符集;Y為有限輸出字符集;I:X→D為X上的D-值子集,表示D-值初始狀態;f:X×U×X×Y→D是D-值輸入-轉移-輸出函數,且f滿足條件:

f(x,u,x′,y)表示在狀態x下,輸入u,到達狀態x′并輸出y的權重。
下面定義M的響應函數(也稱為輸入輸出函數)為φM:U*×Y*→D,?θ∈U*,w∈Y*,若|θ|=|w|時,設θ=u1u2…uk,w=y1y2…yk,
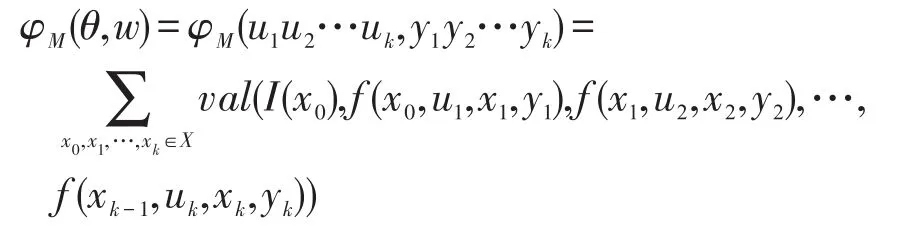
特別地,若θ=w=ε時,則若時,則φM(θ,w)=0 。
定義6一個強賦值加權Mealy機是一個六元組M=(X,U,Y,δ,h,I),其中X、U、Y、I的定義同定義5;δ:X×U×X→D是D-值狀態轉移函數;h:X×U×Y→D是D-值轉移輸出函數,且滿足條件:
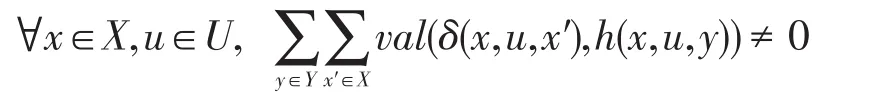
定義M的響應函數為φM:U*×Y*→D,?θ∈U*,w∈Y*,θ=u1u2…uk,w=y1y2…yk,
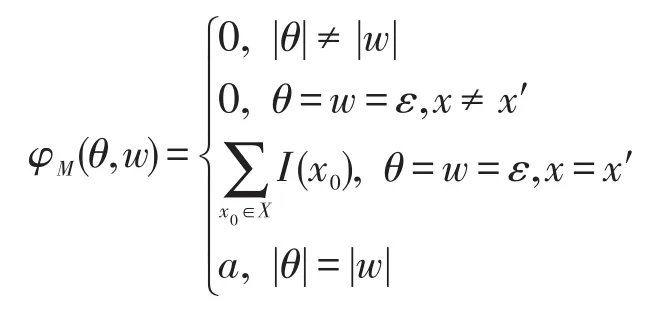
定義7一個強賦值加權Moore機是一個六元組M=(X,U,Y,δ,h,I),其中X、U、Y、I的定義同定義5;δ:X×U×X→D是D-值 狀 態 轉 移 函 數 ;h:X×Y→D是D-值狀態輸出函數,且滿足如下條件:

定義M的響應函數為φM:U*×Y*→D,?θ∈U*,w∈Y*,

其中,當 |w|=|θ|+1 時,設θ=u1u2…uk,w=y0y1…yk,則
特別地,若θ=ε,w=y0時,φM(θ,w)=φM(ε,y0)=
接下來研究強賦值加權序列機與強賦值加權Mealy機的關系。
若強賦值加權序列機M1與強賦值加權Mealy機M2的響應函數相等,即φM1=φM2,則稱二者等價,也即?θ∈U*,w∈Y*,φM1(θ,w)=φM2(θ,w)。
定理1對任意的強賦值加權Mealy機M1,總存在與之等價的強賦值加權序列機M2。
證明任給一個強賦值加權Mealy機M1=(X,U,Y,δ,h,I),構造M2=(X,U,Y,f,I)如下:
即?x∈X,u∈U,上述定義的f滿足強賦值加權序列機中的條件。
因此,M2=(X,U,Y,f,I)是強賦值加權序列機。
?(θ,w)∈U*×Y*,當 |θ|=|w|時,設θ=u1u2…uk,w=y1y2…yk,
本研究考察了不同檢測波長、不同柱溫、不同流速以及不同流動相的樣品色譜圖,根據譜圖分離情況確定色譜條件,具體條件見“2.1”項下。

當 |θ|≠ |w|時,φM2(θ,w)=φM1(θ,w)=0 。
因此,?(θ,w)∈U*×Y*,都有φM2(θ,w)=φM1(θ,w)。□
注2反之,任意的強賦值加權序列機,未必存在與之等價的強賦值加權Mealy機。特別地,當D={0,1}時,任給一個強賦值序列機,也未必存在與之等價的強賦值加權Mealy機,文獻[12]中引理2.1及例2.2對此進行了詳細的證明。
推論1強賦值加權Mealy機與強賦值加權序列機是不等價的。
5 強賦值加權Mealy機與強賦值加權Moore機的關系
下面研究強賦值加權序列機與強賦值加權Moore機的關系。
首先定義機器等價的概念。考慮強賦值加權序列機M1與強賦值加權Moore機M2,假設其具有相同的輸入集合U和輸出集合Y,且響應函數滿足如下的關系式:則稱強賦值加權序列機M1與強賦值加權Moore機M2等價。即可通過驗證是否滿足上述定義中的關系式來判斷強賦值加權序列機與強賦值加權Moore機是否等價。
定理2對任意的強賦值加權序列機M1,總存在與之等價的強賦值加權Moore機M2。
證明任給一個強賦值加權序列機M1=(X,U,Y,f,I),構造M2=(X′,U,Y,δ,h,I′)如下:
因此,M2=(X′,U,Y,δ,h,I′)是強賦值加權Moore機。
這時,M2的響應函數計算如下:
設X′=X×Y={(x0,y′0),(x1,y′1),…,(xk,yk′)}={x0′,x1′,…,xk′},其中:x0′=(x0,y0′),x1′=(x1,y1′),…,xk′=(xk,yk′)。


下面的例子說明了定理2中轉換函數的構造。
例3設D=([0,1],max,val,0,1)是例2中定義的強賦值幺半群,X={x1,x2},U=Y={0,1},f由如下矩陣描述:
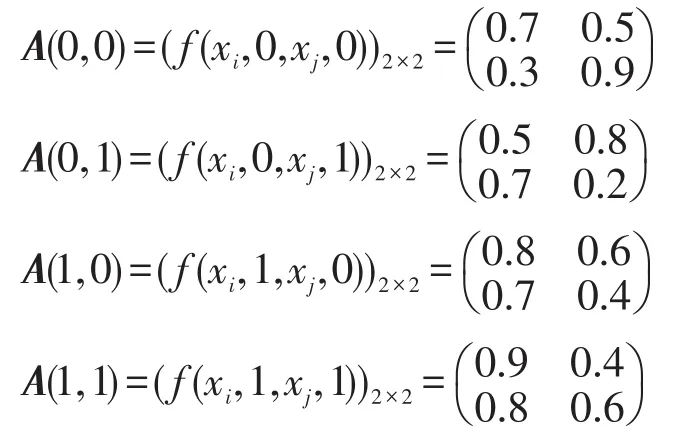


這時M與M′等價。
以θ=01,w=10為例,可得:

因此,φ′(01,110)∨φ′(01,010)=φ(01,10)。
定理3對任意的強賦值加權Moore機M1,總存在與之等價的強賦值加權序列機M2。
證明任給一個強賦值加權Moore機M1=(X,U,Y,δ,h,I),構造M2=(X′,U,Y,f,I′)如下:
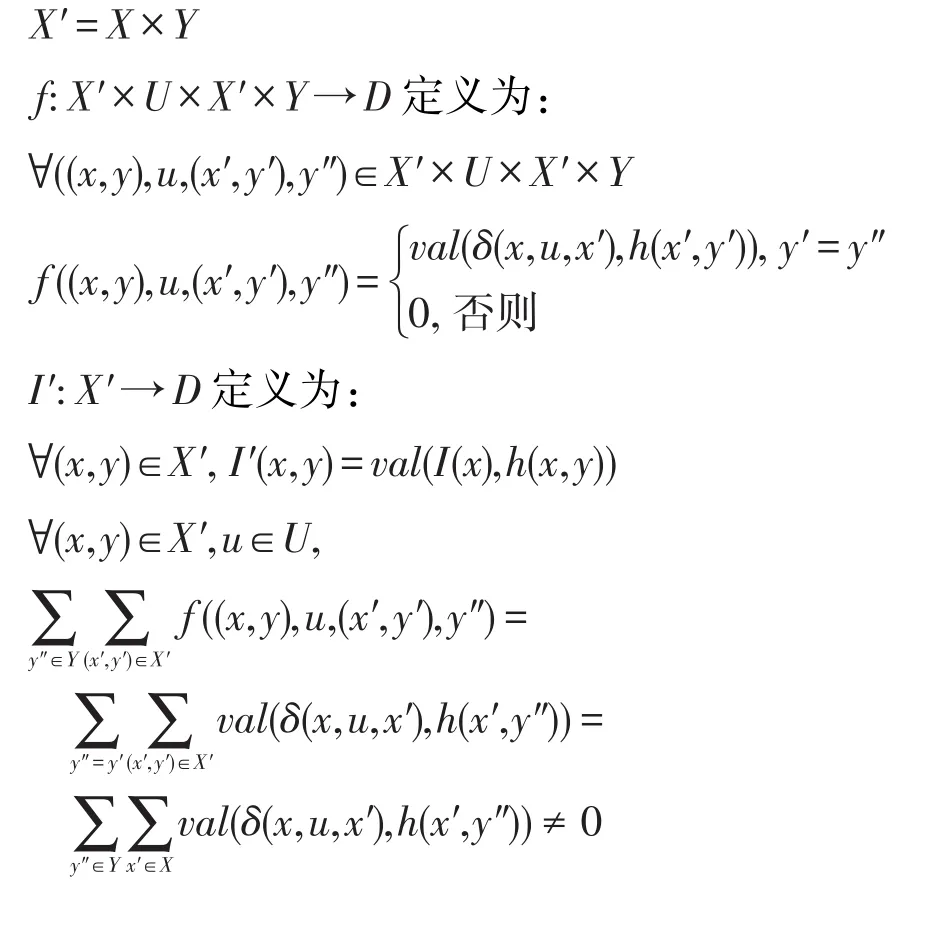
即?(x,y)∈X′,u∈U,上述定義的f滿足強賦值加權序列機中的條件。
因此,M2=(X′,U,Y,f,I′)是強賦值加權序列機。
這時,M2的響應函數計算如下:
設X′=X×Y={(x0,y0′),(x1,y1′),…,(xk,yk′)}={x0′,x1′,…,xk′},其中x0′=(x0,y0′),x1′=(x1,y1′),…,xk′=(xk,yk′)。

下面的例子說明了定理3中轉換函數的構造。
例4設D=([0,1],max,val,0,1)是例2中定義的強賦值幺半群,X={x1,x2},U=Y={0,1},δ與h由如下矩陣描述:
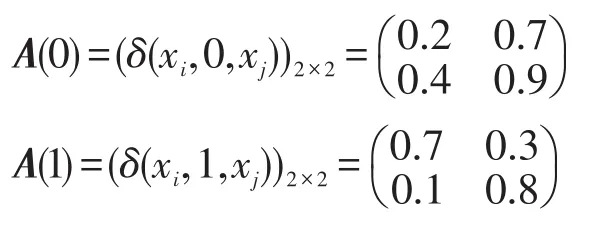

這時M與M′等價。
以θ=01,w=10為例,可得:

定理4強賦值加權序列機和強賦值加權Moore機是等價的。
由定理4和推論1可得推論2。
推論2強賦值加權Mealy機和強賦值加權Moore機是不等價的。
6 總結
本文在權重取值于強賦值幺半群下定義了強賦值加權序列機、強賦值加權Mealy機和強賦值加權Moore機,得到了強賦值加權序列機與強賦值加權Mealy機是不等價的,證明了強賦值加權序列機與強賦值加權Moore機是等價的,并以強賦值加權序列機為中介,得到了強賦值加權Mealy機和強賦值加權Moore機是不等價的。進一步將考慮權重取值于一般的賦值幺半群,以上結論是否也成立。

