單調奇函數的一個性質及其應用

高群安 胡少龍

(湖北省襄州一中 441104)

單調奇函數有下列性質：

若f(x)是定義在R上的單調遞增的奇函數，則(1)f(a)+f(b)=0?a+b=0；

(2)f(a)+f(b)>0?a+b>0；

(3)f(a)+f(b)<0?a+b<0.

若f(x)是定義在R上的單調遞減的奇函數，則

(1)f(a)+f(b)=0?a+b=0；

(2)f(a)+f(b)>0?a+b<0；

(3)f(a)+f(b)<0?a+b>0.

上述性質簡言之：增同減反.證明簡單，這里從略.

這是單調奇函數的一個較為重要而且非常有用的性質，利用這個結論解決有關問題，可縮短思維過程，精簡解題程序，提高解題效率.

一、證明命題

二、求值

例2 已知x,y∈R,x3-3x2+5x=1,y3-3y2+5y=5,求x+y之值.

解題設條件可化為：(x-1)3+2(x-1)=-2,(y-1)3+2(y-1)=2.設f(x)=x3+2x，則f(x)是R上單調遞增的奇函數.

由f(x-1)=-2,f(y-1)=2?f(x-1)+f(y-1)=0，所以x-1+y-1=0?x+y=2.

評注本題通過構造函數，把條件轉化為f(x-1)+f(y-1)=0，利用單調奇函數的性質使問題巧妙解決.

三、解方程

例4 解方程：(x+2018)2017+x2017+2x+2018=0.

解原方程可化為：[(x+2018)2017+(x+2018)]+(x2017+x)=0.設f(x)=x2017+x則f(x)為R上單調遞增的奇函數，由f(x+2018)+f(x)=0得 (x+2018)+x=0?x=-1009.

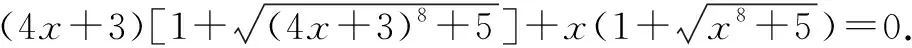
評注例4、例5解答的關鍵是根據方程結構特點，構造奇函數，利用單調奇函數的性質使問題得以解決.

四、求參數范圍

(1)判斷并證明f(x)的奇偶性與單調性；

(2)若f(-2x2+3x)+f(m-x-x2)>0對任意的x∈[0,1]均成立，求實數m的取值范圍.

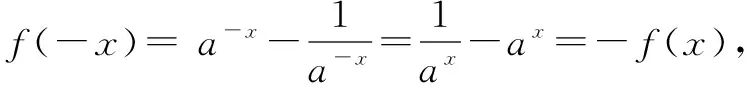
(2)由(1)知f(x)是R上單調遞增的奇函數，所以f(-2x2+3x)+f(m-x-x2)>0對任意的x∈[0,1]均成立?-2x2+3x+m-x-x2>0即m>3x2-2x對任意的x∈[0,1]均成立.因為x∈[0,1]時，3x2-2x的最大值為1，所以m>1. 即所求實數m的取值范圍為(1,+).

(1)求a,b的值；

(2)若對任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立，求k的取值范圍.

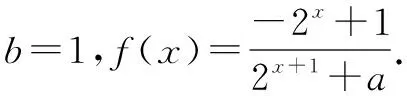
可見利用單調奇函數上述“增同減反”的性質，解決有關問題能夠化復雜為簡單，化抽象為具體，化隱含為顯然，化生疏為熟悉，精簡解題程序，提高解題效率.