相互接觸的兩物體脫離瞬間問題的分析

劉漪榕

(遼寧省撫順市新賓縣高級中學 113200)

對于相互接觸的兩物體脫離瞬間，兩者接觸且無擠壓是此類問題的共同特點，此外題中往往還隱含著兩者速度或加速度的定量關系，下面以幾道習題為例，闡述一下此類問題的處理方法：

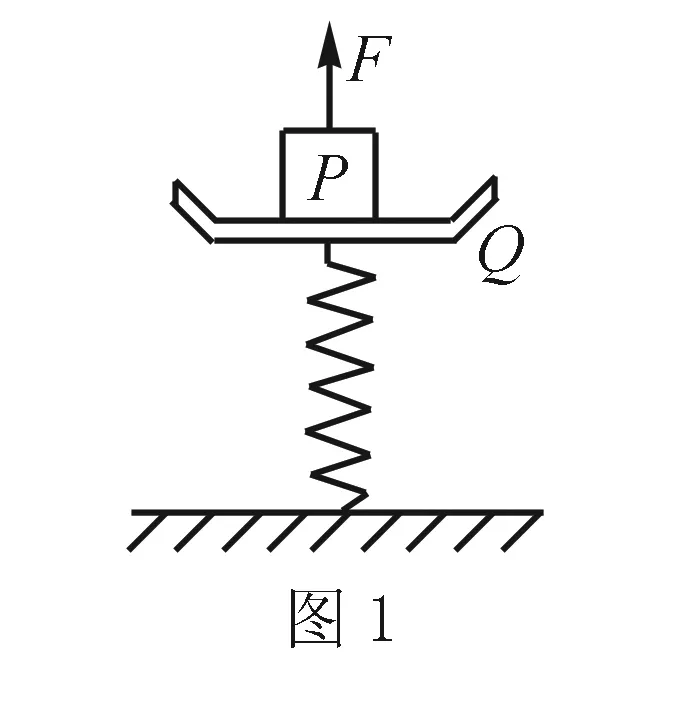
例1 如圖1所示，物體P靜止在臺秤的秤盤Q上，物體P的質量M=10.5kg，秤盤Q的質量m=1.5kg，彈簧的質量忽略不計，彈簧的勁度系數k=800N/m.現給物體施加一個豎直向上的力F，使它向上做勻加速直線運動.已知F在t=0.2s內是變力，在0.2s后是恒力.求F的最大值與最小值.(取g=10m/s2)

分析由題可知，0.2s時為物體P和秤盤Q脫離瞬間，此時兩者速度和加速度均相同，即秤盤具有向上的加速度，所以此時彈簧仍處于壓縮狀態，此時彈簧的壓縮量與初始狀態彈簧壓縮量之差即為0.2s內整體上升的位移，以此入手即可求解.

解設0.2s這一時刻，彈簧被壓縮的長度為x,對秤盤由牛頓第二定律可得：kx-mg=ma.

開始向上拉時，F的值最小，對整個系統，由有牛頓第二定律可得：Fmin=M(+m)a=72 N.

在0.2s時，物體與秤盤恰好分離，此時F的值最大，對物體由有牛頓第二定律可得：Fmax-Mg=Ma，可得Fmax=168N.

例2 如圖2所示，長為L的輕桿的下端用鉸鏈固接在水平地面上，上端固定一個質量為m的小球，輕桿處于豎直位置，同時與一個質量為M的長方體剛好接觸．由于微小擾動，桿向右側倒下，當小球與長方體分離時，桿與水平面的夾角為30°.(不計一切摩擦)．則1.分離時小球和長方體的速率分別為？2.長方體與小球的質量比為？

分析本題中涉及到接觸物系接觸點的速度分解：小球和物塊在垂直接觸面方向的速度和加速度在脫離之前時刻相同.因為脫離瞬間兩者無擠壓，所以物塊的加速度為零，那么此時小球水平方向的加速度同樣為零.又因為鉸鏈輕桿對小球的彈力只能沿桿方向，所以此時輕桿與小球之間也無相互擠壓力，那么小球圓周運動的向心力只能由重力沿法向方向分力提供，再結合系統機械能守恒即可求解.

由m與M構成的系統機械能可得：

例3 如圖3所示，質量為M、表面光滑的半球體靜止放在水平光滑地面上，半球頂端有一個質量為m的小滑塊由靜止開始下滑，至圓心角為θ處時飛離半球體，已知cosθ=0.70,試求M/m的值.

分析本題中對小滑塊m應用牛頓第二定律時，為了方便列式，應以半球M為參考系，因為脫離瞬間二者無擠壓，所以半球M加速度為零，此時仍為慣性系.對于半球M與小滑塊m構成的系統機械能守恒，水平方向動量守恒，列兩個守恒式時是以地面為參考系，所以此題應注意對相對速度的轉換.

以地面為參考系，設滑塊脫離半球瞬間，半球相對于地面的速度為vM，M與m構成系統水平方向動量守恒：m(vmcosθ-vM)=MvM,M與m構成系統機械能守恒：

綜上所述，此類問題一定要挖掘出兩者在脫離瞬間速度或加速度的定量關系，以此為突破口，在結合運動學，牛頓運動定律，能量，動量的相關知識便可求解.