例析函數單調性在解題中的應用
許萬成
(江蘇省建湖縣第二中學 224700)
函數的單調性是函數的三個重要性質之一,在解決函數問題時有著廣泛的運用.對函數的單調性考查是高考的熱點,多數情況下是以中檔題形式呈現.為了使同學們對函數的單調性有一個更好的認識,筆者根據自己平時的教學,將平時利用函數的單調性來解決的常見題型以例題的形式呈現給讀者.
一、確定函數的單調性(區間)
例1 函數f(x)=f(x)=log1/2(x2-4)的單調遞增區間為( ).
解析由x2-4>0,得x>2或x<-2.
所以f(x)的定義域為(-,-2)∪(2,+).
令t=x2-4,則y=log1/2t(t>0).
因為t=x2-4在(-,-2)上是減函數,且y=log1/2t在(0,+)上是減函數,所以f(x)在(-,-2)上是增函數,即f(x)單調遞增區間為(-∞,-2).
答案:D


當a<0時,f(x1)-f(x2)<0,即f(x1) 當a>0時,f′(x)<0,函數f(x)在(-1,1)上遞減; 當a<0時,f′(x)>0,函數f(x)在(-1,1)上遞增. 評注(1)求函數的單調區間,應先求定義域,在定義域內求單調區間,如例1. (2)函數單調性的判斷方法有:①定義法;②圖象法;③利用已知函數的單調性;④導數法. (3)復合函數y=f(g(x))的單調性應根據外層函數y=f(t)和內層函數t=g(x)的單調性判斷,遵循“同增異減”的原則. 評注解函數不等式:首先根據函數的性質把不等式轉化為f(g(x))>f(h(x))的形式,然后根據函數的單調性去掉“f”,轉化為具體的不等式(組),此時要注意g(x)與h(x)的取值應在外層函數的定義域內. 例5 (2017天津,理6) 已知奇函數f(x)在R上是增函數,g(x)=xf(x).若a=g(-log25.1),b=g(20.8),c=g(3),則a,b,c的大小關系為( ). A.a C.b 解析因為f(x)是奇函數且在R上是增函數,所以在x>0時,有f(x)>0,從而g(x)=xf(x)是R上的偶函數,且在[0,+)上是增函數.a=g(-log25.1)=g(log25.1).20.8<2,又4<5.1<8,則2 評注比較大小是高考常見題,指數式、對數式的比較大小要結合指數函數、對數函數,借助指數函數和對數函數的圖象,利用函數的單調性進行比較大小,特別是靈活利用函數的奇偶性和單調性數、形結合不僅能比較大小,還可以解不等式. 例6 如果函數f(x)=ax2+2x-3在區間(-,4)上是單調遞增的,則實數a的取值范圍是( ). 解析(1)當a=0時,f(x)=2x-3,在定義域R上是單調遞增的,故在(-,4)上單調遞增. 評注利用單調性求參數. ①視參數為已知數,依據函數的圖象或單調性定義,確定函數的單調區間,與已知單調區間比較求參數; ②需注意若函數在區間[a,b]上是單調的,則該函數在此區間的任意子集上也是單調的; ③分段函數的單調性,除注意各段的單調性外,還要注意銜接點的取值.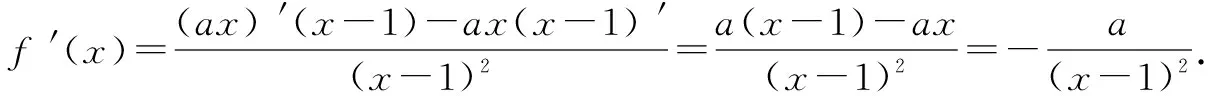
二、利用函數單調性求值域或最值
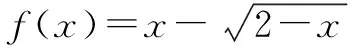

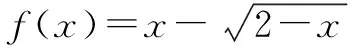


三、利用單調性解不等式



四、利用單調性比較兩個函數值或自變量的大小
五、利用函數單調性求參數范圍