基于統計分析的卷積神經網絡模型壓縮方法①

楊 揚,藍章禮,陳 巍

(重慶交通大學 信息科學與工程學院,重慶 400074)

2012年Hiton[1]構建的深度卷積神經網絡AlexNet才在圖像分類領域取得了驚人的成績,卷積神經網絡(CNN)在計算機視覺領域包括圖像分類[1],目標檢測[2]、圖像語義分割[3]、視頻分類[4]得到了廣泛的應用[5].之后,層數更多、更加精細設計的深度卷積神經網絡結構相繼被提出,比如VggNet[6]、GoogLenet[7]、ResNet[8]在ImageNet[9]上取得了更好的成績.除此之外,卷積神經網絡在人工智能[10],自然語言處理[11],故障診斷[12]有著廣闊的應用前景.這些深度卷積神經網絡模型參數越來越多,運算量越來越大,對運算設備的內存、CPU、GPU的配置要求越來越高.當需要在運算和存儲資源有限的微型設備上[13],比如手機、嵌入式設備上使用卷積神經網絡時,除了準確率,計算效率和模型的大小也是至關重要的.

模型壓縮最早的研究為OBD[14](Optimal Brain Surgeon)和OBS[15](Optimal Brain Surgeon),通過泰勒展開,分析參數的擾動對損失函數的影響,以此確定參數的重要性,決定參數保留或者裁剪.Han等人[16]通過裁剪、量化、壓縮卷積神經網絡模型參數,大幅度減少模型的大小,并且沒有降低模型的準確率.文獻[17]指出非結構的稀疏無法利用現有的硬件進行加速,提出了一種在目標函數上增加group lasso進行結構化稀疏的學習方式.文獻[18]通過一個訓練好的較大的模型來訓練一個較小的模型,將較大的模型學到的知識遷移到較小的模型中.Network in Network[19]除了對卷積層進行了改進,還提出了全局平均化的方法,解決了全連接層參數數量多的問題,并被GoogleNet和ResNet等采用.目前卷積層的卷積核大小、卷積核數量對于不同的數據集參數設置不同,需要大量實驗,有一定經驗成分,卷積層用一般包含了足夠多數目的卷積核,存在冗余,已有相關文獻通過實驗證明在裁剪部分不重要的卷積核后,再訓練整個卷積神經網絡(或者逐層裁剪、逐層訓練)可以在盡量不損失準的條件下對卷積神經網絡進行壓縮[20–22].Wen[20]等人通過定義APoZ(Average Percentage of Zeros)來統計每一個卷積核中激活為0的比例,以為評估一個卷積核是否重要,主要是用在最后一層卷積層,以此減少全連接層的參數數量.文獻[21]通過將一定樣本輸入卷積神經網絡,計算特征圖的各類參數,對活性低的特征圖通道裁剪.文獻[22]通過將卷積核參數的L1范數作為評價一個卷積核重要性的依據,將不重要的卷積核裁剪.

由于文獻[19]提出的全局平均池化在一定會程度上解決了傳統卷積神經網絡參數多的問題.本文的主要解決的是卷積層的壓縮,在調研了卷積神經網絡訓練過程中的規律的基礎上,提出了基于卷積核的標準差作為卷積核重要性指標進行卷積核裁剪的方法,并和文獻[22]相結合的方法,通過實驗,本文提出的方法能和文獻[22]互補,綜合兩種評價指標綜合進行卷積核裁剪能保留對分類更有作用的卷積核.

1 卷積神經網絡的原理

1958年,Hubel和Wiesel等人[23]發現了生物視覺系統的信息處理方式,視覺信息從視網膜傳遞到大腦是通過多層的感受野激活完成的.1998年,Lecun等人[24]提出的LeNet-5,如圖1所示,LeNet-5由兩層卷積層和兩層池化層交替將輸入圖像轉換成一系列特征圖,再連接三層全連接層對提取的特征分類.卷積層的卷積核實現了局部感受野和特征提取的功能,將局部區域信息通過卷積核的卷積運算,再經過激活函數、池化,將低層的激活信息傳遞到高層.以往的人工設計的特征有良好的特征表達能力,例如HOG[25],SIFT[26],但這些人工設計的特征缺乏良好的泛化能力.池化層也稱下采樣層,能在一定程度上保持特征的尺度不變性并對特征圖降維.Lenet提出后,在圖像分類領域沒有取得實質的進展和突破,直到2012年Hiton及其學生Alex構建的深度卷積神經網絡AlexNet在ImageNet上取得了顯著的成績,主要原因是訓練的改進,在網絡的訓練中加入了權重衰減、Droupout[27]、Batch Normalization[28]等技術,更關鍵的是計算機計算能力的提升,GPU加速技術的發展,使得在計算機可以高效地實現卷積的運算.之后,更復雜,準確率更高的深度卷積神經網絡被提出.

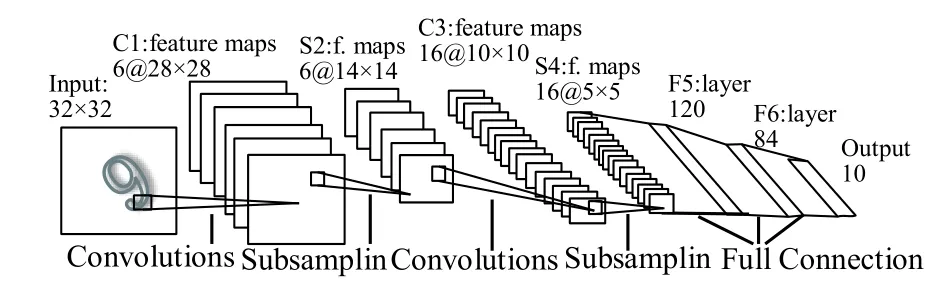
圖1 LeNet-5結構圖

如圖2所示,為一個5×5×3的卷積核作用在一個32×32×3的圖像(也可能為32×32×3的特征圖)上,5×5×3的卷積核與圖像的5×5×3區域點乘再加上偏置(bias)經過激活函數,產生一個運算結果,即圖中的小圓球.卷積核在圖像的所有局部區域以步長為1滑動并卷積,得到一個28×28×1的特征圖(feature map).

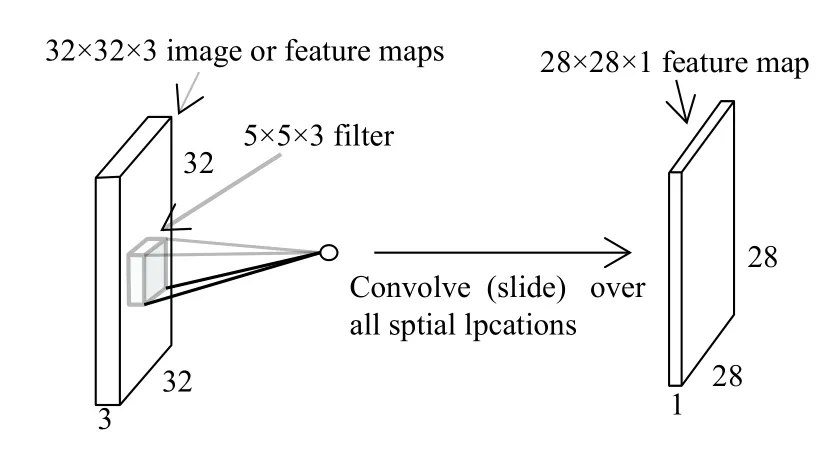
圖2 一個卷積核作用在圖像或者特征圖上

同理,如圖3所示,32×32×3的圖像經過一個有6個5×5×3的卷積核的卷積層,產生了28×28×6的特征圖.在實際中,滑動的步長不一定為1,有時為了保持卷積后特征圖大小不變或者取整,會對特征圖的邊界進行填充(padding),特征圖通過卷積層后,會接著通過池化層(pooling layer),將得到的特征圖輸入到下一層卷積層.

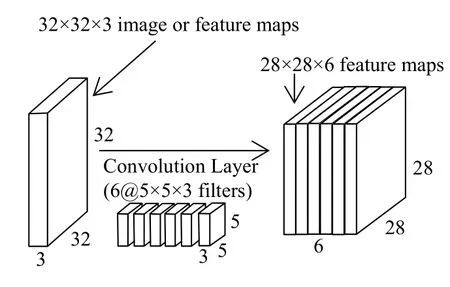
圖3 6個卷積核作用在圖像或者特征圖上

2 卷積核的裁剪

近年來,為了讓卷積神經網絡達到更好的效果,卷積神經網絡朝著更深更復雜的方向發展.而另一方面,增強深度神經網絡的運算效率,在不損失精度的情況下,對深度學習訓練得到的模型進行優化壓縮也有著大量的研究.本文參照文獻[21,22]提出的卷積核裁剪方式,針對已經訓練好的卷積神經網絡模型,對卷積層中數個不重要的卷積核裁剪,同時裁剪對應的特征圖,最后對裁剪后的模型進行再訓練,恢復模型的性能.

2.1 裁剪方式

為了便于說明裁剪卷積核的方式,如圖4所示,Xk∈RHK×WK×NK代表第k層的特征圖,Hk、Wk、Nk分別是其高、寬、維度,Convk∈Rs×s×NK×NK+1為第k層卷積層,Fi,j∈Rsk×sk為其中一個2D的單層卷積核,i=1,2,…,Nk,j=1,2,…,Nk+1,sk為第k層卷積層卷積核的高和寬,Nk、Nk+1分別為上一層的特征圖的維度和下一層特征圖的維度.Xk層特征圖通過第k層卷積層Conv k得到了k+1層特征圖Xk+1,假設在卷積層中刪除第j個卷積核,即圖中Convk的j列(灰色),同時也裁剪了Xk+1層特征圖的第j個特征圖.減少的參數,減少的計算量為,在k+2層特征圖Xk+2的計算過程中額外將少的乘法運算量為Nk+2×s2k+1×Hk+2×Wk+2.當在第k層卷積層中裁剪m(0≦m＜nk+1)個卷積核時,減少的參數為,減少的乘法運算量為Hk+1.

2.2 卷積核的評價指標

為了決定一個卷積層中某個卷積核的重要程度,文獻[20]通過定義APoZ(Average Percentage of Zeros),即一個卷積核中來統計每一個卷積核中激活為0的比例,以為評估一個卷積核是否重要,主要是用在最后一層卷積層,以此減少全連接層的參數數量.文獻[21]通過輸入樣本,通過計算特征圖的相關參數確定卷積核的重要程度,認為對不同樣本得到類似特征圖的卷積核為冗余的卷積核.通過文獻[22]在提出以卷積核的L1作為卷積核重要程度的評價指標,認為裁剪L1范數較小的卷積核對整個模型影響較小.

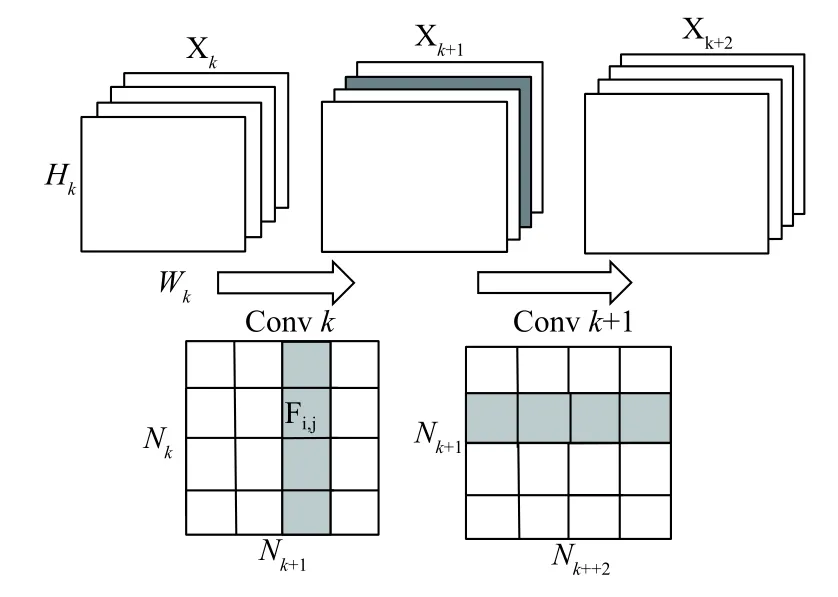
圖4 卷積核的裁剪方式

卷積神經網絡訓練過程中,卷積層中參數的標準差(或方差)逐漸增大,分布范圍逐漸擴大,參數之間的差異性逐漸明顯,如圖5、圖6所示.

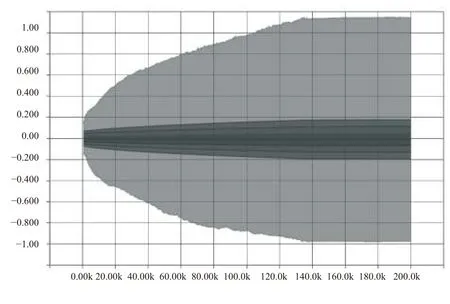
圖5 Conv 2參數在訓練過程中的分布

本文認為,卷積神經網絡通過訓練,標準差或者方差更大的卷積核學習到了更明顯的局部特征,因此提出了基于標準差的卷積核裁剪方法,克服了文獻[20,21]需要輸入樣本,統計特征圖各類參數需要額外大量計算量的缺點,同時也避免了文獻[22]只保留L1范數較大的卷積核,而沒有考慮到卷積核提取特征的能力與參數的分布有關.本文了還將以卷積核標準差作為卷積核重要性指標與文獻[22]提出的以卷積核L1范數作為卷積核重要性指標相結合,即將卷積核的L1范數和標準差結合作為卷積核重要性的評價指標,對卷積核進行裁剪.

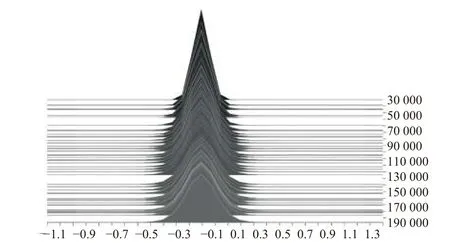
圖6 Conv 2參數在訓練過程中的統計直方圖

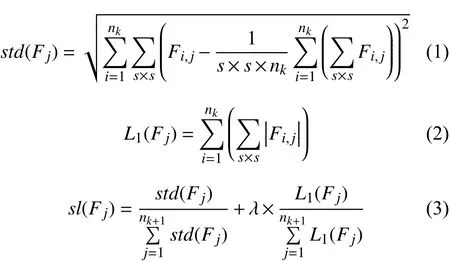
式(1)為一個卷積層中第j個卷積核的標準差計算公式,代表對Fi,j中s×s個元素進行求和.式(2)為卷積層第j個卷積核的L1范數計算公式,代表對Fi,j中s×s個元素的絕對值進行求和,即Fi,j的L1范數,nk個單層卷積核Fi,j的L1范數和即為卷積核Fj的L1范數.式(3)同時考慮了卷積核的L1范數和標準差,為了防止L1范數和標準差計算結果相差過大,對卷積核L1范數和標準差進行了歸一化處理,參數λ調節卷積核L1范數和標準差的相對重要程度.當λ=1時,表示卷積核L1范數和標準差同等重要,當λ＜1時,表示卷積核標準差比L1范數更重要,當λ>1時,表示卷積核L1范數比標準差更重要.

3 實驗分析

為了驗證本文所提出的卷積核裁剪方法的正確性和有效性,本文在MNIST和Cifar-10數據集上分別設計了有兩層卷積層和三層卷積層的卷積神經網絡進行了實驗.實驗環境:Ubuntu 16.04,Python3.6,Tensorflow 1.2,計算機CPU為6700 hq,GPU為GTX 960 m(4 G顯存),內存為8 G.

對MNIST數據集和Cifar-10數據集分別設計了兩層卷積層和三層全連接、三層卷積層和三層全連接層結構的卷積神經網絡,如表1所示,Conv k代表第k層卷積層,(3,3,1,32)代表該層有32個3×3×1的卷積核.FC k代表第k層全連接層,(3136,200)代表輸入一個3136維的數組,輸出一個200維的數組.由于cifar-10數據集更復雜,所以在訓練過程中采用了數據增強和權重衰減.兩個卷積神經網絡都采用了交叉熵損失函數計算代價函數.在訓練完成后,在MNIST數據集上的正確率達到了99.02%,在Cifar-10上的正確率達到了86.56%.

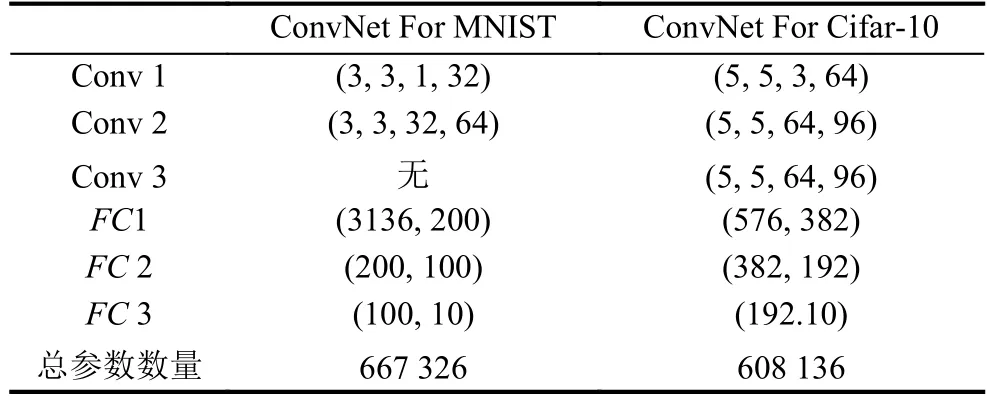
表1 所設計的卷積神經網絡的結構

3.1 據方差裁剪卷積核對比

從圖7和圖8可以看出,在用MNIST數據集訓練得到的帶有兩層卷積層的神經網絡中,裁剪標準差較小的卷積核能比裁剪標準較大的卷積核保留的準確率更高,即標準差較大的卷積核比方差較小的卷積核更重要,證實了本文的設想,即標準差較大的卷積核在訓練的過程中學到了更為重要的局部特征.

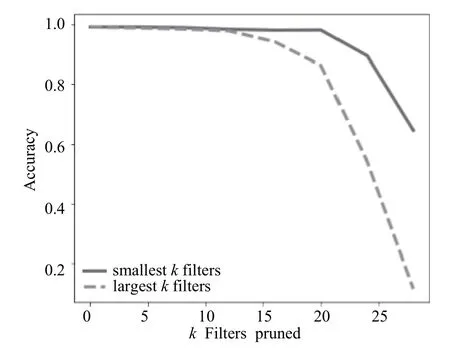
圖7 裁剪針對MNIST訓練的卷積神經網絡第一層卷積層中的卷積核

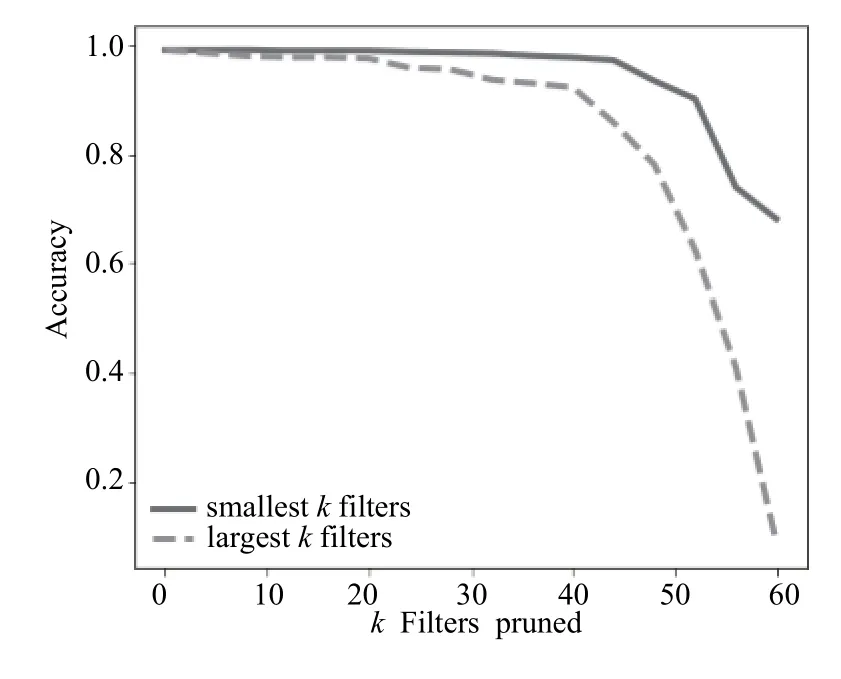
圖8 裁剪針對MNIST訓練的卷積神經網絡第二層卷積層中的卷積核

如圖9-圖11可以得出,在Cifar-10上也有著類似的結果,在針對MNIST數據集設計的卷積神經網絡中,在裁剪甚至50%的卷積核時,準確率沒有明顯降低.而針對Cifar-10數據集設計的卷積神經網絡,裁剪少數卷積核準確率也會明顯降低.一方面是因為MNIST數據集較為簡單,Cifar-10數據集較為復雜,其次是因為針對MNIST數據集設計的卷積神經網絡卷積核設置得較多,這也說明了,在訓練好的卷積神經網絡模型中,如果在一個卷積層中裁剪一定的卷積核而準確率沒有明顯降低,說明這一層的卷積核設置的過多,可以對卷積核進行裁剪.

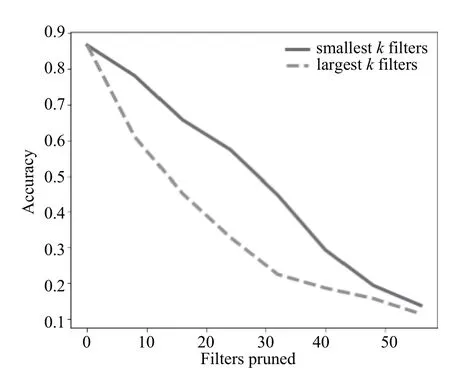
圖9 裁剪針對Cifar-10訓練的卷積神經網絡第一層卷積層中的卷積核

3.2 對比實驗

為了驗證本文提出的方法的有效性,本文在分別針對MNIST和Cifar-10訓練好的卷積神經網絡模型與其他的裁剪方式進行了對比,式(3)中λ取值為1.卷積神經網絡在裁剪后,性能會有一定的下降,為了恢復性能,一般會在對裁剪后的模型進行再訓練,再訓練的迭代次數一般沒有從初始狀態訓練多.24-48代表經過裁剪,第一層卷積層的卷積核保留的個數為24,第二層保留的個數為48,其余情況以類似的方式表示.

圖10 裁剪針對Cifar-10訓練的卷積神經網絡第二層卷積層中的卷積核

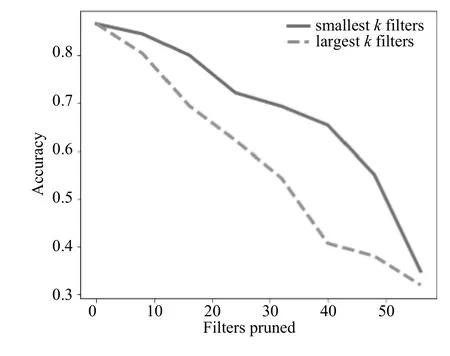
圖11 裁剪針對Cifar-10訓練的卷積神經網絡第三層卷積層中的卷積核

通過表2可以看出,對MNIST數據集設計的兩層卷積神經網絡分別裁剪后,通過方差作為評價卷積核的裁剪能保留更多的準確率,同時通過再訓練后得到的準確率也比文獻[22]的方式高.通過表3可以看出,針對Cifar-10設計的三層卷積神經網絡中,在48-64-64這種方式裁剪時,文獻[22]提出的L1范數作為卷積核的評價指標保留了較大的準確率,而在32-48-48這種裁剪方式時,本文提出的方法保留了較高的準確率,而通過再訓練準確率會有所損失.選取L1+std作為卷積核的評價指標進行裁剪時,裁剪后的準確率在L1和std之間.因此,式(3)中的參數λ可以通過卷積核裁剪的比例動態動態調整,在裁剪卷積核數量過多時,適當增大λ,可以保留更高的準確率.

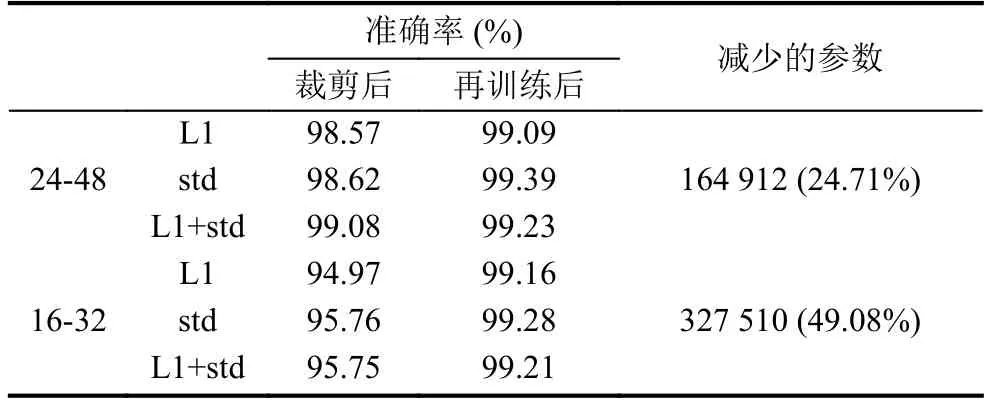
表2 裁剪針對MNIST數據集訓練的兩層卷積層神經網絡

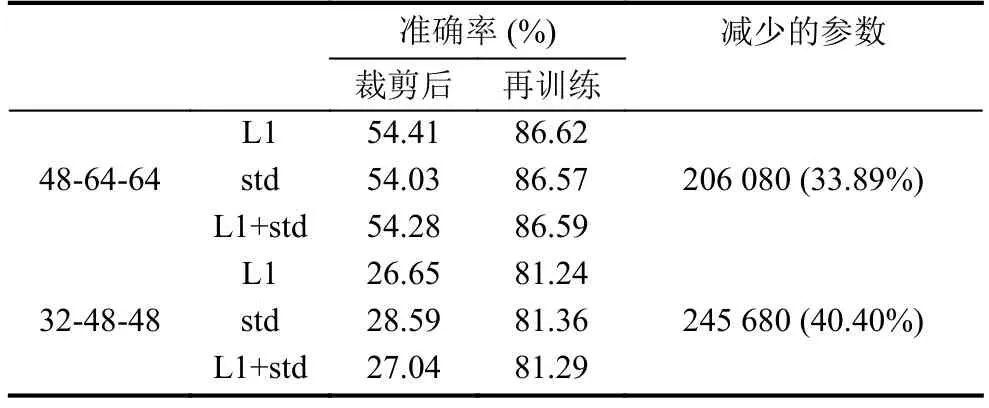
表3 裁剪針對Cifar-10數據集訓練的三層卷積層神經網絡

4 結論與展望

本文從卷積神經網絡訓練過程中參數的統計特征出發,提出了一種基統計分析裁剪卷積核的卷積神經網絡模型壓縮方法.通過在針對MNIST和Cifar-10所設計的兩個卷積神經網絡中進行裁剪實驗,本文提出的標準差較大的卷積學習到了更顯著的局部特征的設想是正確的,在與類似的裁剪方式的對比中,本文提出的方法在裁剪較多的卷積核時保留更高的準確率,根據裁剪的比例動態調整卷積核L1范數和標準差的相對重要程度,可以使得裁剪的結果更穩定.在后續的研究中,將進一步研究卷積核通道間的裁剪和利用特征圖使得裁剪結果最優.