風電盤式制動器溫度場有限元分析
尚振國, 蔡衛國, 高吭
(大連海洋大學機械與動力工程學院,遼寧大連116023)
0 引言
圖1所示為某1.5 MW風力發電機用盤式制動器,其工作原理是用底座將制動器整體固定于機架上。制動時首先打開放油口將碟簧施力機構內的液壓油放出,碟簧彈開驅動主動鉗上的制動片壓緊制動盤,制動盤安裝于增速齒輪箱輸出軸上,從而實現整臺風機制動停車。由于齒輪箱輸出軸功率大、轉速高,因此制動時制動片和制動盤不但磨損量大,而且發熱和溫升也很嚴重,從而加劇摩擦片和制動盤的磨損,影響制動器的性能及壽命。因此對風電制動器進行溫度場分析,對于提高制動器性能及改進設計,具有十分重要的意義。目前有很多學者開展了車用盤式制動器的熱力學分析研究,如王若平等[1]應用ABAQUS軟件建立某型牽引車盤式制動器熱力學有限元分析模型,研究制動盤溫度場和應力場的分布特性,并用臺架試驗驗證仿真結果的正確性。葛振亮等[2]應用ANSYS的熱-結構模塊建立汽車盤式制動器有限元模型,研究緊急制動工況下制動盤溫度分布規律。指出制動盤溫度分布的不均勻性將產生熱應力和熱疲勞,導致制動盤產生裂紋或出現碟形翹曲變形,并給出改進措施。孟祥寶等[3]在ANSYS中用熱流密度來模擬某汽車盤式制動器摩擦生成的熱量,研究制動過程中制動盤溫度變化情況。秦嶺等[4]通過ABAQUS模擬汽車制動盤在緊急制動過程中熱-結構耦合特性的情況,分析了制動盤的熱疲勞失效特性及壽命。而目前關于風電盤式制動器熱力學分析方面的研究內容則較少,主要是因為風力發電機轉動慣量大、轉速高、制動距離大,若采用汽車盤式制動器的模擬摩擦生熱過程的熱力學分析方法,則會造成計算量過大、計算時間過長等問題。因此這里提出一種基于ANSYS多載荷步和熱流密度的有限元分析方法,為風力發電機等大慣量、高轉速機械設備制動器溫度場分析提供一種有效的途徑。
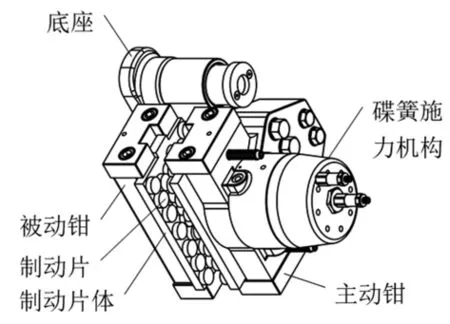
圖1 風電盤式制動器
1 運動學分析
制動器的運動學方程如下:

式中:M為制動力矩,N·m;Mf為阻力矩,N·m;Ie為風機等效轉動慣量,kg·m2;ε為角加速度,rad/s2;ω為角速度,rad/s;ω0為制動初速度,rad/s;t為制動時間,s;θ為制動距離,rad。
2 熱流密度
假定制動過程中動能全部轉化為熱能傳遞給制動盤和制動片,則在制動盤與制動片接觸面上產生的熱流密度q為

式中,A為制動盤與制動片接觸面積。
摩擦接觸面上熱流分配率α為[5]

因制動盤雙面都與制動片接觸,故

式中:q1、q2分別為制動盤和制動片熱流密度;λ1、λ2分別為制動盤和制動片比熱容;ρ1、ρ2分別為制動盤和制動片密度;C1、C2分別為制動盤和制動片熱導率。
3 對流換熱
制動盤面平均對流換熱系數計算公式為[6]:

式中:κα為空氣的導熱系數,κα=0.0276 W/(m·K);D為制動盤的外直徑;Re為雷諾數,Re=ωραD2/(2μα),其中:ω為制動盤轉速;ρα為空氣密度,ρα=1.13 kg/m3;μα為空氣動力黏度,μα=1.91 kg·s/m。
4 有限元模型
1)單元類型和網格化分。單元采用SOLID70,該單元具有3個方向的熱傳導能力,有8個節點且每個節點上只有1個溫度自由度,可以用于三維靜態或瞬態的熱分析。采用掃掠法(Sweep)進行網格劃分,如圖2所示。

圖2 有限元模型
2)載荷施加。考慮傳導和對流的影響,忽略熱輻射的影響[7-8]。由式(4)~式(6)分別計算出制動片和制動盤上的熱流密度。在ANSYS軟件中將制動片上的熱流密度定義成一個關于時間的函數表,再將這個熱流密度表施加于制動片接觸面上。由于制動盤是轉動的,因此如何在制動盤上施加熱流成為一個關鍵問題。這里將整個制動過程定義成多個載荷步。在每個載荷步根據制動盤轉過角度計算轉動時間、轉動速度以及熱流密度,再選擇盤面上對應節點,將熱流密度施加于所選節點上,形成一個旋轉的熱流載荷步系列,如圖3所示。
由式(7)計算出對流換熱系數,施加于制動盤兩接觸面上,如圖3所示。

圖3 旋轉的熱流載荷步系列示意圖
5 算例分析
以圖1所示風電盤式制動器為例,其材料屬性及結構尺寸見表1。在分析中將材料參數看作不隨溫度變化的常數。

表1 材料屬性
制動力矩M=9000 N·m;阻力矩Mf=8200 N·m;風機等效轉動慣量Ie=365 kg·m2;制動初速度ω0=188.5 rad/s。由此,得制動時間t=4 s,制動距離θ=377 rad=60 r。將表1中數據代入式(5),得
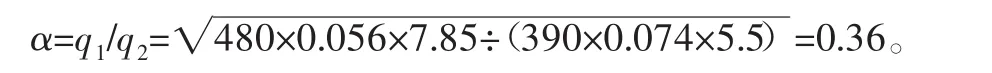
結合式(6)可得q1=0.132q,q2=0.368q。
有限元模型如圖2所示,制動盤共劃分7371個單元,10 092個節點;制動片共劃分1000個單元,1331個節點。
5.1 溫度場特征
如圖4所示,制動片上最高溫度達961.03℃,但仍低于燒結金屬許用溫度(1000℃以上)[9];在其下面的制動片體的溫度接近設定的環境溫度。可見熱量主要聚集在制動片表面,沿軸向(厚度方向)溫度下降梯度較大。這是因為制動過程中摩擦熱產生速度遠遠高于制動盤、片內部熱傳導的速度[10]。由于制動片體升溫很小,制功熱對制動片體后面的間隙調整機構、施力機構等影響可不用考慮。如圖5所示,制動盤面摩擦區(圖上深色區)溫度最高720.7℃,非摩擦區(圖上淺色區)溫度接近設定的環境溫度。摩擦區和非摩擦區的邊界地帶溫度梯度很大,將會產生較大的熱應力,需要格外注意。制動盤內部溫度約400℃。軸向溫度下降梯度也較大。
5.2 制動力矩對溫度場影響

圖4 制動片溫度云圖

圖5 制動盤溫度云圖
為研究制動力矩對溫度場的影響,分別將制動力矩設定為額定制動力矩的110%、100%和85%來計算溫度場分布,如圖6所示。可見,制動片上溫度先升高后下降,而且初期升溫速度很快,在制動過程中期稍后溫度達到最高值。這是因為在制動中前期,制動盤轉速快,輸入熱量大于傳導、對流等散熱量,所以溫度上升。在制動后期,制動盤轉速下降,輸入熱量小于傳導、對流等散熱量,因此溫度下降。制動盤由于雙面受熱,輸入熱量始終大于傳導、對流等散熱量,因此溫度持續升高,直至制動過程結束。
在110%額定制動力矩情況下,制動時間縮短為3.8 s,制動片上最高溫度達到1026℃,存在超過燒結金屬許用溫度的危險,制動盤最高溫度達到765℃。在85%額定制動力矩情況下,制動時間變為4.34 s,制動片上最高溫度為852℃,制動盤最高溫度達到656.8℃。雖然制動時間有所延長,但制動溫度降低也較為明顯,因此在操作時應嚴格控制制動力矩。

圖6 最高溫度隨時間變化曲線
5.3 制動盤熱應力分析
由于制動盤徑向尺寸較大,熱膨脹以及較大的溫度梯度將導致盤內產生較大的熱應力,因此有必要進行熱-結構耦合分析[11-13]。基本過程是將熱力學單元轉換為結構單元[14-15];把先前熱力學分析結果作為溫度載荷施加到節點上;對制動盤與制動片接觸區域及制動盤中央內孔表面施加位移全約束。應力云圖如圖7所示。最大熱應力為80 MPa,出現于制動盤與制動片接觸區邊角位置,因為這些位置存在應力集中現象。其余非接觸區域由于可以自由膨脹,因此熱應力很小。內孔表面由于熱變形受到約束,因此熱應力也較大,約為60 MPa。而制動力在制動盤內產生的機械應力較小,壓應力為1.6 MPa,周向剪切應力為0.6 MPa,可見制動盤內應力主要為熱應力。

圖7 制動盤熱應力云圖
6 結 論
1)制動盤和制動片溫升較大,并且存在溫度梯度較大的區域,導致出現較嚴重的熱應力。2)制動力矩對溫度場影響較大,因此可適當降低制動力矩,在制動時間增加不多的情況下換取制動溫度的明顯降低,提高制動器安全性。3)算例分析表明基于多載荷步和熱流密度的有限元熱力學分析方法可以很好地模擬制動過程,是解決風電制動器溫度場及應力場計算分析問題的一種行之有效的方法。

