齒輪參數圖像的軟件識別

伍哲， 郭文勇， 張文群

（海軍工程大學動力工程學院，武漢430033）

0 引言

齒輪作為傳遞運動和動力的基礎零件在機械設備中運用極其廣泛，齒輪參數的測量隨著其他領域技術的發展而不斷進步。傳統的接觸式測量方法較復雜，價格昂貴，對設備的使用和維護成本較高，給實際的測量帶來了很大的麻煩。隨著計算機技術的發展，數字圖像處理是一門新技術，數字圖像處理函數算法的出現，使圖像處理速度越來越快，精確度越來越高，操作越來越方便，而且具有非接觸性可視化[1-3]、自動化和智能性高等優點，可廣泛應用于各種實時在線的齒輪精密測量。

1 齒輪原始圖像預處理

1.1 灰度變換處理

本齒輪圖像采用SolidWorks軟件建模，在不同背景不同比例尺下完成的原圖設定，在識別原圖像時，增加處理時間，也會導致后期處理的麻煩，因此，將原圖轉化為灰度圖像是有必要的。根據三基色原理，每一種光都可以分解成紅、綠、藍三種基礎顏色光。所謂的灰度圖像是指在RGB三基色系統中[4]，從最暗的黑色到最亮的白色的灰度3個分量值R、G、B按不同的比例混合成各種顏色，經過這樣的前期變換，會縮短后期圖像處理時間。利用MATLAB圖像處理工具箱中的函數即實現將RGB圖像轉換為灰度圖像程序[5]如下：

本文選取兩組圖片（A組照片為兩圖片在不同偏轉角度的同一黑色背景顏色，B組為在同一背景顏色的不同齒輪顏色），研究哪種因素對實驗結果的影響偏大，并研究該因素對實驗結果產生怎樣的影響。

圖1 齒輪角度不同時對齒輪讀取

圖2 齒輪顏色不同時對齒輪讀取

圖3 經MATLAB處理后所得灰度圖像

1.2 增強灰度圖像

圖4 增強的灰度圖像

灰度圖像處理是將含有亮度和色彩的圖像變換成只含亮度圖像的過程，為了提高圖像清晰度，顯示圖像所需要的細節部分，增強對比度，需要增強圖像的灰度級別[6]，對圖像的后期處理更加方便，故對灰度圖像進一步處理后的圖像為增強高度灰度級圖像，其運行程序如下：

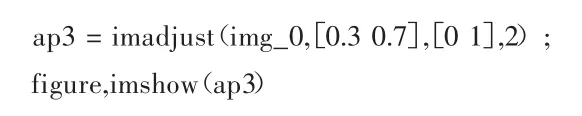
1.3 圖像的邊緣檢測

邊緣檢測是圖像處理的基本問題，經過檢測的圖像可以剔除不相關的信息保留圖像的結構屬性。MATLAB中提供了一種edge函數用于灰度圖像的邊緣檢測，本文采用canny方法[7]進行圖像的邊緣檢測，這種方法抗噪聲干擾的能力很強，能夠較為全面地檢測到圖像的邊緣，也包括讀取困難的弱邊緣輪廓，因此運用越來越廣泛了。經邊緣檢測處理后的圖片效果如圖5所示。

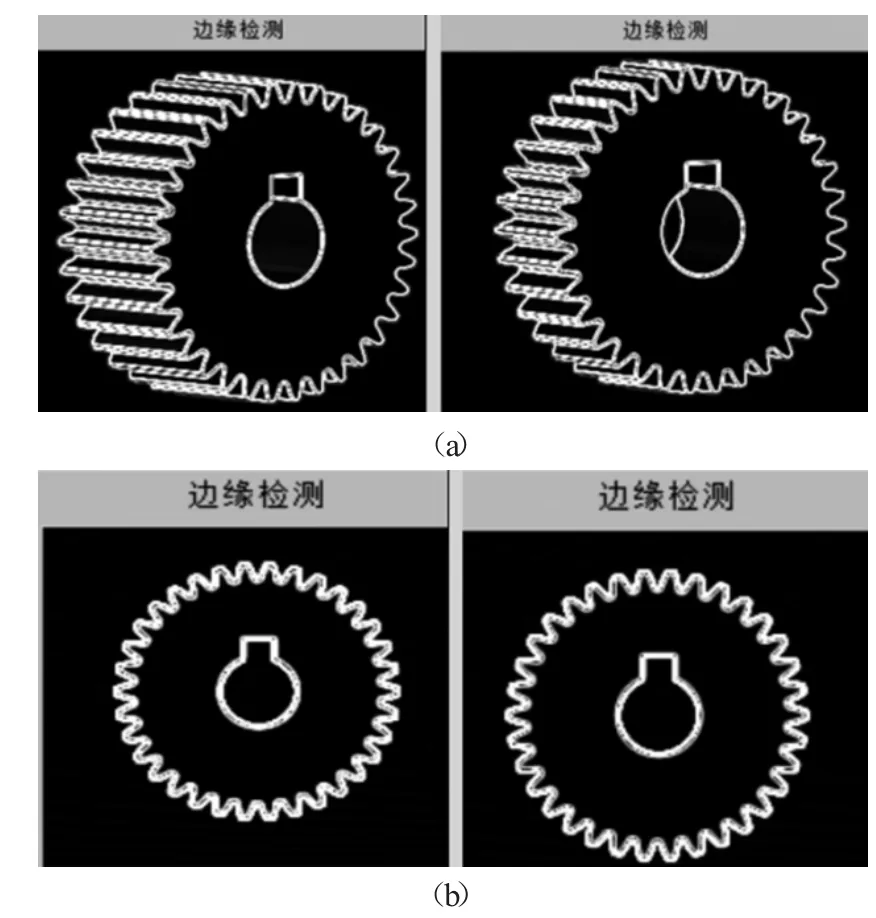
圖5 齒輪邊緣檢測圖像

經比較，A組同一比例尺不同偏轉角度下，圖1顯示黑色背景，圖2在原圖白色背景下處理結果，很好地顯示了弱邊緣。處理程序如下：

1.4 灰度圖像的直方化處理

該直方圖是灰度函數處理所得，它表示經處理后的圖像中具有某種灰度級的像素出現的次數，其中橫坐標是灰度等級，縱坐標是該灰度級出現的次數，在圖像處理中直方圖概括了一個圖像灰度級內容。MATLAB中提供了imhist函數[8]來實現灰度圖像的直方化，處理后灰度圖像層次分明，相當于增加了圖像的對比度，使圖像看起來更加清晰。處理圖像程序如下：

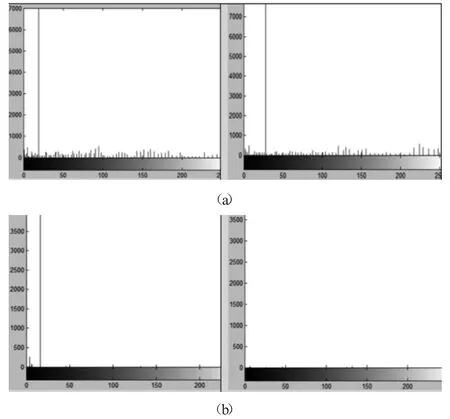
圖6 齒輪圖像直方化

1.5 齒輪圖像的填充

本文中用于分析的齒輪模型是具有鍵槽的，在確定齒輪中心點或質心坐標的過程中提供參照，在MATLAB中，imfill函數[9]用于實現圖像區域孔洞的填充，在圖片處理的灰度圖像中幾個點圍成的空洞區域即要填充的區域，本文給出的齒輪模型中間的鍵槽就是需要填充的區域，對于質心和中心位置的確定很有幫助。填充圖像程序如下：

圖7 齒輪圖像的填充

2 齒輪參數的確定

運用MATLAB處理齒輪圖像的最終目的就是獲得相對精確的基本的齒輪參數數據，進而利用公式計算出其他參數。直齒圓柱齒輪的參數有很多，但決定齒輪齒形和尺寸的基本參數只有5個，即齒輪齒數z、模數m、壓力角a、齒頂高系數h、齒隙系數c，上述5個參數均已標準化；通過軟件的識別技術，在確定齒輪中心點的前提下可以測得齒輪分度圓直徑，通過公式計算求得齒輪任意參數，是一種比較實用的方法。

2.1 齒輪中心點的確定

齒輪中心點的確定是在齒輪圖像中用坐標表示的，即便在不同的比例尺下也可以確定，對于不帶鍵槽的直齒圓柱齒輪，可以利用重心法、最小二乘法的圓擬合法、Hough圓檢測法確定中心[10]；對于帶鍵槽的直齒圓柱齒輪，中心點的檢測只能用最小二乘法的圓擬合法、Hough圓檢測法；對于沒有內孔的齒輪，采用重心法比較合適。齒輪圖像經過二值化后所有的灰度值非1即0，找出齒輪上灰度值為1的像素點，將其橫坐標xi和縱坐標yi，分別除以像素點的個數n;就可以得到近似的齒輪圓心座標（x0，y0），確定圓心的程序如下：

圖8 齒頂圓圓心點的確定

2.2 齒頂圓半徑的確定

通過上一步確定了齒輪的圓心以及前面的圖像處理過程，可以清楚地讀取出齒頂圓或者齒根圓的直徑，利用公式da=m（z+2）或df=d-2hf=m（z-2.5）便可以得到齒輪模數。中心確定后就可以搜索出齒輪邊界上的點參考中心點的相對坐標。假如前期圖像預處理比較理想，那么齒頂圓和齒根圓接近圓，在圖片讀取的過程中得到相對精確的數據。在理想情況下，假設從齒輪輪廓某點處展開在齒輪輪廓標記點到中心的距離是一個周期函數，并且齒根和齒頂在同一高度，因此所得的齒頂圓不變。測量齒輪齒頂圓半徑程序如下：

L=bwlabel（M,8）;%標記連通區域通道為8

stats=regionprops（L）;%由于圖像的截取原因，圖像最上邊有一個白色目標

將所得結果取平均，弱化誤差

R1=stats（2）;Bounding Box（3）/2

R2=stats（2）;Bounding Box（4）/2

所得的結果，其齒頂圓半徑分別為r1=19.3 mm、r2=15 mm、r3=19.5 mm、r4=20.5 mm。

2.3 齒輪參數的確定

在前面已經測得了齒輪齒頂圓直徑，可以由公式da=m（z+2）計算出m的值，由于模數已經標準化，然后利用此計算的大致結果與GB 1357-87中的標準模數系列進行對比，取得相近的值[11]。在上文中顯示的齒頂圓直徑以及公式計算的結果，對照標準模數表選取模數m=2。

2.4 實驗結果誤差分析

正確認識誤差的性質，分析誤差產生的原因，設計、選用合理的測量儀器從根本上減小誤差，得到更加接近真實值的數值，誤差是測量值與被測量真值之間的差。本文中齒輪是由SolidWorks建模所得到的，在建模過程中所確定的圖形尺寸齒頂圓半徑為20 mm，齒數為34，但在程序運行過程中圖片處理、中心點的確定、尺寸的讀取都會存在偏差[12-19]，因此可以通過絕對誤差和相對誤差來分析，如表1所示。

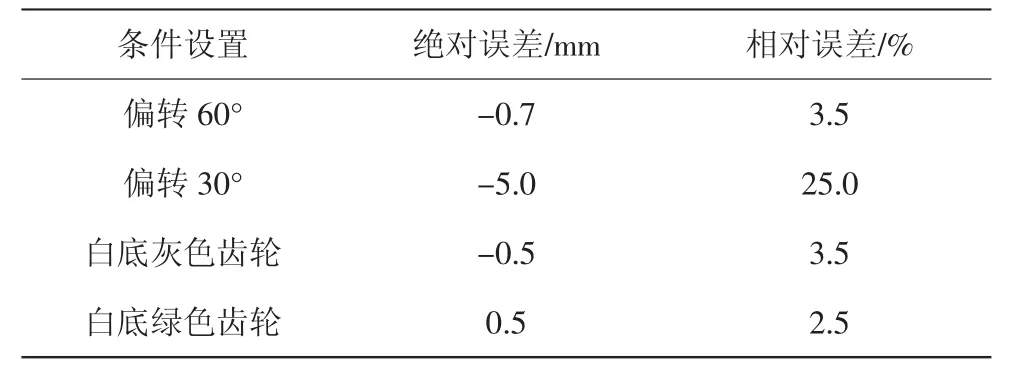
表1 絕對誤差和相對誤差分析

3 結語

通過上面的誤差分析可以得到：在齒輪偏轉接近60°和齒輪顏色接近亮色時得到的齒輪參數數據比較接近理論值。本文利用一種簡單的成本低廉非接觸式方法測量齒輪的參數，在工程中可以運用到小而且精度要求高的齒輪測量上，給實際工作帶來很大的方便；在文中僅僅描述一種測量漸開線標準圓柱齒輪齒頂圓的算法，但對于擁有眾多基本參數的齒輪，這種算法還有很多不足之處。