基于關鍵點的不確定時間序列線性降維方法
2018-08-21 01:59:42湯其婕朱小萍
計算機技術與發展 2018年8期
湯其婕，朱小萍
(南京航空航天大學 計算機科學與技術學院，江蘇 南京 211106)
0 引 言
時間序列(time series)是一種典型的高維數據類型，也是數據挖掘[1-2]領域中主要研究的對象。一條時間序列是一組序列數據，它通常是在相等間隔的時間段內，依照給定的采樣率，對某種潛在過程進行觀測的結果。它廣泛存在于工業、農業及商業等領域，與人們的生活息息相關。其典型數據包括航天飛船等重要儀器每一時刻的運行狀態數據、醫療設備記錄的病人每時每刻的心率變化等。研究如何有效地從這些復雜的海量時間序列中挖掘潛在的有用信息，具有重要的理論價值與現實意義[3-4]。
在實際生產生活中，時間序列的產生通常受不確定因素的影響，如數據采集設備的缺陷和環境影響，導致數據采集與實際數據有一定的偏差；或者出于隱私安全考慮，人為地將一定程度的偏差引入到數據中。這些偏差導致時間序列在每一個點上的取值對應一個可能值的集合，無法給出其確定值。將這類型的數據定義為不確定時間序列。加之時間序列本身具有的海量、高維等特征，若直接對原始不確定數據進行數據挖掘等操作，效率很低。而解決這一問題最直接的方法就是對原始數據進行預處理操作。但是由于不確定時間序列與確定時間序列在取值上的不同之處，原有用于確定時間序列上的方法則不適用于不確定時間序列。因此，結合已有的針對確定數據的處理方法，找到適用于不確定時序數據的預處理方法，是目前針對不確定時間序列研究的重點，也是文中主要研究的問題。
文中主要研究了基于關鍵點的線性降維算法與統計模型相結合的不確定時間序列線性降維問題。首先對不確定時間序列進行有效的描述統計建模，將不確定時間序列歸約為三條確定的時間序列，進行空間維度的一次降維；然后分別對三條確定時間序列進行關鍵點的選取，進行時間維度的二次降維；最后，綜合空間維度和時間維度的兩次降維，得到整個不確定時序數據集的關鍵點，完成整個降維工作。
1 相關工作
1.1 線性表示的提出
針對確定時間序列的預處理，已有許多成熟的方法，如傅里葉變換[5](DFT)、離散小波變換[6](DWT)、奇異值分解[7](SVD)等等。以上幾種方法在某些方面具有明顯的優勢，但是也存在不足。例如，傅里葉變換、離散小波變換存在一個共同缺點，即過度除噪。消除了局部極值點，造成重要信息遺失，數據表示誤差較大；奇異值分解法依賴數據，該方法由于使用數據集產生新的基向量，數據項的任何改變都需要重新計算，時間復雜度大。基于以上幾種算法的不足，時間序列線性表示[8-9]方法被提出，其主要目的是有效地保留數據的主要特征，對數據進行高效的降維處理。
1.2 傳統時間序列的線性表示
傳統的時間序列線性表示方法的主要思想就是用一系列前后相互連接的線段近似表示原始數據，其關鍵之處在于分段點的選用[10]。線性表示在時間序列的應用上有如下幾個優點：理論簡單，實現容易；壓縮率可以調整。既保留數據的特點，又進行有效的降維。近年來，國內外許多學者對線性表示方法進行了深入研究，提出了許多優秀的線性表示方法。文獻[11-12]各自獨立提出了分段聚合近似(PAA)的時間序列線性表示方法，該方法的主要思想是首先將時間序列按照相同的時間跨度進行劃分，然后以每個時間序列子段的平均值來近似表示相應子段。文獻[8]介紹了一種基于重要點的線性表示方法(PLR-IP),即如果一個點在局部區間內與區間端點的比值超過設定的閾值R，則認為它是重要點。通過調節閾值R，可以獲得不同精度的線性表示。文獻[9]介紹了基于特征點的線性表示方法(PLR-FP)，該方法的思想是首先提取時間序列的極值點，然后根據每個極值點保持的時間跨度去除噪聲點。文獻[13]介紹了一種基于斜率提取邊緣點的時間序列線性表示方法(PLR-SEEP)，該方法的主要思想是首先設定閾值，然后根據斜率變化選取分段點。
2 不確定時間序列描述統計模型建模
不確定時間序列與傳統時間序列相比，主要的不同之處在于每個時間點的取值。前者是一個取值的集合，且每一個數值對應該數值在該時間戳發生的概率，后者是一個確定的數值。因此，針對傳統時間數據對數值的處理，需要轉換為對集合的處理。
定義1(集中趨勢)：在描述統計學中，觀察值在分布中心位置的聚集現象稱為分布的集中趨勢，一個分布中心特征的統計度量稱為集中趨勢的度量。數據集中，平均值是最常用、最具代表性的度量。其中，算數平均值，是整體數學期望的無偏估計。大數定律規定，隨著重復次數接近無窮大，數值的算術平均值幾乎肯定地收斂于期望值(expected value)。因此，文中選擇觀察值集合的期望值作為觀察值的集中趨勢度量，記為vt,ey，表示不確定時序數據的集中趨勢。例如，給定某一時間點的觀察值及對應的概率{(5,0.3),(6,0.4),(7,0.2),(8,0.1)}，則該點的集中趨勢為5×0.3+6×0.4+7×0.2+8×0.1=6.1。
定義2(MME-Line不確定時間序列)：長度為n的MM-Line不確定時間序列由一條包含n個元素的序列構成，記為：
TSUMME-Line={([v1,min,v1,max],v1,ev),([v1,min,v1,max],v1,ev),…,([vn,min,vn,max],vn,ev)}
(1)
其中，每個元素是一個二元組，由該時刻的觀察值區間及其集中趨勢組成；ti表示第i個時刻，序列中所有時刻的最大觀察值所構成的序列叫作最大值序列，其相連之后所得曲線叫作最大值曲線，記為Max-Line。同樣，所有最小觀察值構成最小值序列，相連后曲線記為Min-Line；所有集中趨勢構成集中趨勢序列，記為EV-Line。例如，不確定時間序列TSUMME-Line={([2.5,4.2]，3.3)，([3.6,7.9]，5.5)，([4.5,9.2]，7.6)，([3.8,7.2]，6.2)，([6.0,10.8]，8.3)，([5.1,9.6]，9.6)}，所有最大觀察值(3.3,7.9,9.2,7.2,10.8,9.6)構成Max-Line序列，所有最小值(2.5,3.6,4.5,3.8,6.0,5.1)構成Min-Line序列，所有集中趨勢(3.3,5.5,7.6,6.2,8.3,9.6)構成EV-Line序列。
定義3(MME-Line描述統計模型)：不確定時間序列描述統計模型包括三條等長的確定時間序列：Max-Line、Min-Line和EV-Line。因此，不確定時間序列MME-Line的向量形式表示如下：
(2)
其中，XMax-Line為Max-Line序列；XMin-Line為Min-Line序列；XEV-Line為集中趨勢序列。
由此，對不確定時間序列的降維可以歸約為對這三條確定時間序列的降維。
3 基于關鍵點的不確定時間序列線性降維
3.1 選取關鍵點
關鍵點是反映時間序列數據特征的重要點，也是對時序數據進行分段的點，體現了時間序列的輪廓和集中趨勢。如圖1所示，圖中1、2處的關鍵點是典型的極值點，其可以通過極值法求出；但3～5處的轉折點并不能通過極值法求出，而文獻[8]證明，該類型的點在時間序列數據集中也是包含大量重要信息的數據點。文中關鍵點的選擇包括極值點和轉折點兩部分。
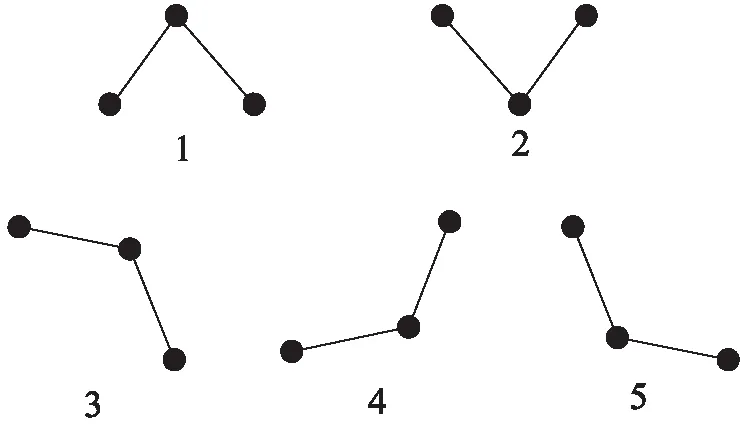
圖1 關鍵點舉例
定義4(轉折點)：在不超過序列的最大值和最小值下，由三點組成的簡單時間序列，夾角越小，角處的頂點成為轉折點的可能性就越大。將該點稱為轉折點。
定義5(閾值參數)：由三點組成的時間序列，A、O、B，其端點O是否為轉折點，決定于三點數值是否滿足條件|Data(A)+Data(B)-2*Data(O)|≥C。其中C即是自定義的閾值參數，其大小決定于所選數據的類型，Data(*)表示在時間點*處的數值。
數據的壓縮程度可以通過調節閾值參數來設置。閾值參數設置越大，則數據壓縮程度越大；反之，數據壓縮程度越小，數據分段越精細。
3.2 選取關鍵點算法
由3.1可知，關鍵點的選擇包含極值點和轉折點兩部分。通過對描述統計模型中的三條確定時間序列分別進行關鍵點的選取，可以得到三個關鍵點的集合，分別是Max-Line關鍵點集合、Min-Line關鍵點集合和EV-Line關鍵點集合。算法的具體過程如下。
算法：MME-KP
輸入：不確定時間序列TSU={(t1,V1,P1),(t2,V2,P2),…,(tn,Vn,Pn)}，閾值參數C1、C2、C3，時閾參數T
輸出：三條確定時間序列關鍵點集合
1 double []MaxNum; double []MinNum; double []EVNum;
2 for(i=0;i<1;i++){
3 sort(Vi);
4 vi,ey=pi,1*vi,1+pi,2*vi,2+…+pi,n*vi,n;
5 MaxNum[i]=vi,max; MinNum[i]=vi,min; EVNum[i]=vi,ey;}
6 ArrayList MaxKP; ArrayList MinKP; ArrayList EVKP;
7 for(i=0;i8 if(MaxNum[i]是極值點){
9 MaxKP.add(i);
10 }else if(MaxKP[i]是轉折點 && !MaxKP.contains(i){
11 MaxKP.add(i);
12 }
13 }//MinKP和MaxPV的計算與MaxPV類似
14 MaxKP=getKPArrayList(MaxKP, T); //對關鍵點進行進一步篩選，使其滿足時間跨度T
15 MinKP=getKPArrayList(MinKP, T);
16 EVKP=getKPArrayList(EVKP, T);
3.3 算法分析
MME-KP算法首先通過提出的描述統計模型將不確定時間序列歸約為3條確定時間序列，即最大值序列、最小值序列和集中趨勢序列，有效提取了數據的三個主要特征。其次，對三條歸約得到的確定時間序列分別進行兩遍掃描選取關鍵點。其中關鍵點包含了極值點和轉折點兩部分，基本保留了數據的全部特征。同時，該時間序列線性降維算法綜合考慮了時間跨度的選擇，可以根據不同數據的特點動態設置閾值參數C和時閾參數T，改變數據選取的精細程度和數據的壓縮度。綜上，該算法既能較好地保留時序數據的特征關鍵點，同時又能有效降維。算法的復雜度為O(n),n為時間序列的長度[14]。
4 實 驗
4.1 實驗目的和實驗環境
為了驗證文中提出的基于關鍵點的線性降維算法與描述統計模型相結合的實際效果，選取了10個不同領域的時間序列數據集進行實驗。實驗以壓縮率和擬合誤差作為評價優劣的指標，將MME-KP算法與PAA算法以及PLR-FP算法進行對比。
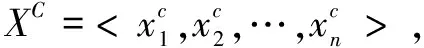
(3)
擬合誤差是用來衡量擬合時間序列與原始時間序列差異性的一個重要指標。在同等壓縮率的情況下，擬合誤差越小，表示擬合效果越好，擬合數據越接近真實數據。
4.2 實驗數據處理
確定時間序列是一組按時間先后順序排列的精確數據，這些數據通過加入擾動成為不確定化數據，由此成為不確定時間序列。給定某一時刻i，不確定時間序列在該時刻的值可表示為：
Vi=di+ei
(4)
其中，di為確定時間序列i時刻的精確值；ei為該時刻誤差，通常服從某種概率分布。
文中實驗數據取自于www.cs.ucr.edu/～eamonn/tutorials.html公布的用于數據挖掘的通用實驗數據集(KP-Data)，如表1所示。將每個數據集的訓練子集和測試子集重新配置整合，獲得實驗數據集。同時，通過不確定化模型將不確定性引入到確定序列中，人為加入擾動形成誤差ei，并使ei服從某種分布，從而將序列轉化成不確定時間序列。
表1 KP-Data數據集
4.3 實驗方法
實驗主要分為兩部分：
(1)將原始數據進行統計模型建模，每種類型的數據將分別建模得到三條確定時間序列數據：最大值序列、最小值序列和集中趨勢序列；
(2)在步驟1建立的模型基礎上，分別用提出的MME-KP算法、Yi和Keogh提出的分段聚集近似(PAA)線性表示方法，以及文獻[9]提出的PLR-FP線性表示方法對數據分別進行處理，得到整個不確定時序數據集的關鍵點集合。最終以同種壓縮率的標準下擬合誤差的大小作為評估算法質量的指標。擬合誤差越小，算法性能越好。
4.4 實驗結果與分析
(1)第一部分。
在提出的統計模型下，部分數據的建模表示如圖2所示。
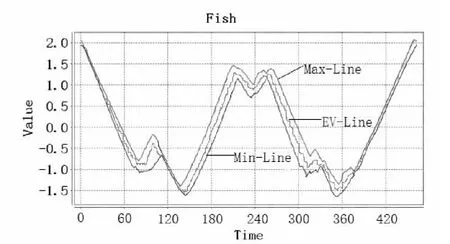
(a)Fish原始數據圖
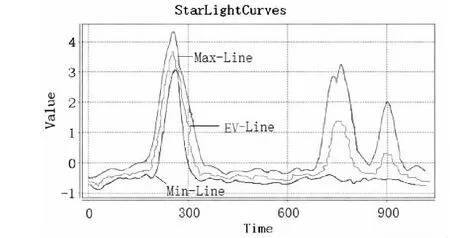
(b)StarLightCurves原始數據圖
(2)第二部分。
文中提出的MME-KP需要輸入3個閾值參數：C1、C2和C3，分別對應三條確定時間序列，即最大值時間序列、最小值時間序列及集中趨勢時間序列的關鍵點閾值參數。參數設置越大，數據的壓縮率越小，擬合誤差越大；參數設置越小，數據壓縮率越大，數據分段越精細，擬合誤差越小。實驗選取的數據來自10個不同領域，數據的差異性較大。為了對比實驗的公平性，將根據不同數據類型調整參數，保證在10組數據的壓縮率都在50%的基準下，進行三種算法的擬合誤差對比。在同一壓縮率情況下，擬合誤差越小，算法性能越好。
部分實驗結果如圖3所示。
從圖3中可以看出，在10個通用時間序列數據集中，MME-KP算法在其中7個數據集上Max-Line擬合序列的誤差最小，在另外三個數據集中，誤差與最好的算法相當。同時，由圖(b)可以看出，在EV-Line上的擬合誤差，MME-KP算法明顯優于其他兩種算法，在10個數據集中都保持優勢。實驗結果說明，采用了極值點與轉折點相結合的選取關鍵點算法，在數據降維上具有明顯優勢。因為其在保留了極值點這一數據的明顯特征外，還適當選取了體現數據特征的轉折點，減小了一些重要點被粗暴舍棄的概率，提高了數據選取的精細度，從而降低了擬合誤差。
(a)三種算法在Max-Line上擬合誤差的比較
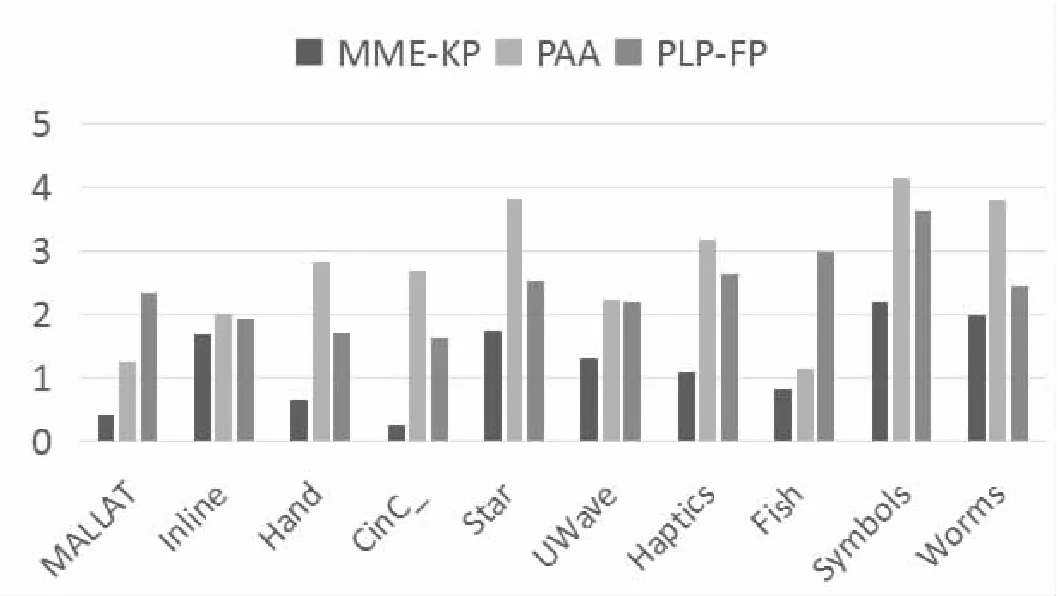
(b)三種算法在ME-Line上擬合誤差的比較
同時實驗結果顯示：對于短時間內波動頻率比較平緩的時間序列，MME-KP算法的實驗效果與其他兩種算法相比，優勢并不是很大，如圖4中的對比1所示，MME-KP算法和PAA算法都能較好地擬合MALLAT的原始數據。但是對于短時間內波動頻率劇烈的時間序列，如圖4中的對比2所示，數據在短時間內波動較大，MME-KP算法的擬合效果就遠勝于PAA算法。主要原因是，在短時間內，時間序列波動較大，會產生大量極值點，對于以找極值點和轉折點為主要關鍵點的MME-KP算法來說會捕獲大量關鍵點，從而保證了數據主要特征的不流失。而對于PAA算法，它主要思想是以一段時間內的數據均值來代替這段序列，所以，在短時間內時間序列波動較大的情況下，在這段時間內的數據均值波動并不會很大，相對地，它的擬合序列與原序列相比，就會丟失很多重要點信息，造成擬合誤差較大。
綜上，MME-KP降維方法在與提出的描述統計模型的結合上，有以下幾點優勢：在降維效果上，可以通過參數的改變，進行不同壓縮率的降維。參數設置越高，數據壓縮程度越大。在現實應用中可以根據實際需求選擇所需的降維效果；在與其他線性降維方法PAA以及PLR-FP的比較過程中，MME-KP方法體現出了更為良好的擬合效果，誤差更小，與原始數據保持高度的一致性。
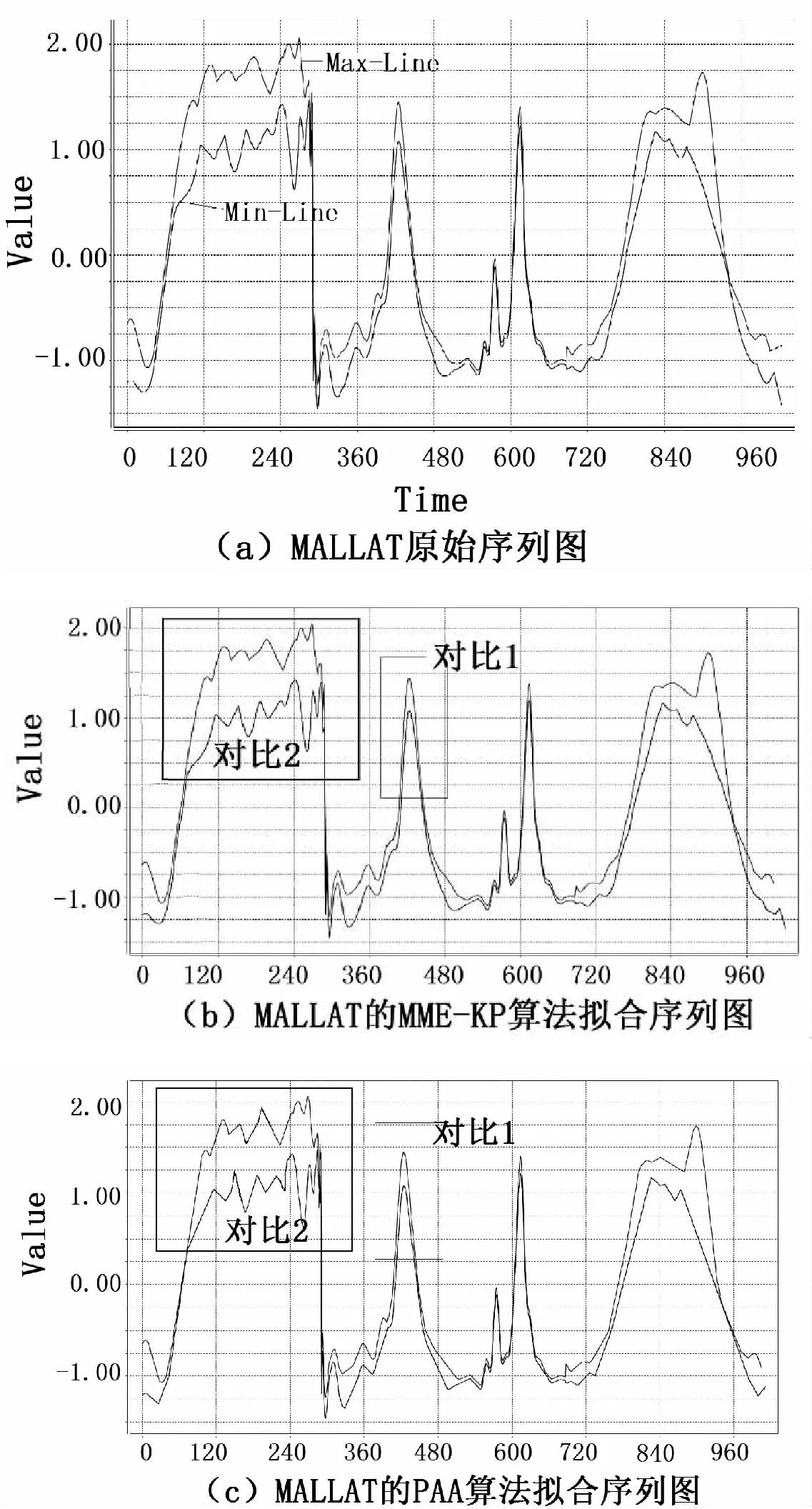
圖4 實驗對比
5 結束語
針對不確定時序數據區別于確定時序數據的主要特征，首先提出不確定時間序列向確定時間序列歸約的描述統計模型，同時綜合考慮已有的確定時間序列的線性分段思想，提出綜合考慮極值點與轉折點的關鍵點選取算法。綜合以上兩點，將不確定時序數據進行空間和時間上的有效降維。實驗結果表明，該算法在數據降維效果上有良好的性能，且能高度還原原始數據。下一步的研究工作是在所提出模型的基礎上找到更合適的原始數據擬合方案。
猜你喜歡
聚焦金屬關鍵點中學生數理化·中考版(2022年12期)2022-02-16 07:36:56 肉兔育肥抓好七個關鍵點今日農業(2021年8期)2021-11-28 05:07:50 學習方法兒童故事畫報(2019年5期)2019-05-26 14:26:14 豬人工授精應把握的技術關鍵點河南畜牧獸醫(2016年24期)2016-11-29 01:28:30 用對方法才能瘦Coco薇(2016年2期)2016-03-22 02:42:52 四大方法 教你不再“坐以待病”！Coco薇(2015年1期)2015-08-13 02:47:34 賺錢方法小雪花·成長指南(2015年7期)2015-08-11 15:03:12 捕魚小雪花·成長指南(2015年4期)2015-05-19 14:47:56 醫聯體要把握三個關鍵點中國衛生(2014年2期)2014-11-12 13:00:16 鎖定兩個關鍵點——我這樣教《送考》語文知識(2014年7期)2014-02-28 22:00:26
8 if(MaxNum[i]是極值點){
9 MaxKP.add(i);
10 }else if(MaxKP[i]是轉折點 && !MaxKP.contains(i){
11 MaxKP.add(i);
12 }
13 }//MinKP和MaxPV的計算與MaxPV類似
14 MaxKP=getKPArrayList(MaxKP, T); //對關鍵點進行進一步篩選，使其滿足時間跨度T
15 MinKP=getKPArrayList(MinKP, T);
16 EVKP=getKPArrayList(EVKP, T);
3.3 算法分析
MME-KP算法首先通過提出的描述統計模型將不確定時間序列歸約為3條確定時間序列，即最大值序列、最小值序列和集中趨勢序列，有效提取了數據的三個主要特征。其次，對三條歸約得到的確定時間序列分別進行兩遍掃描選取關鍵點。其中關鍵點包含了極值點和轉折點兩部分，基本保留了數據的全部特征。同時，該時間序列線性降維算法綜合考慮了時間跨度的選擇，可以根據不同數據的特點動態設置閾值參數C和時閾參數T，改變數據選取的精細程度和數據的壓縮度。綜上，該算法既能較好地保留時序數據的特征關鍵點，同時又能有效降維。算法的復雜度為O(n),n為時間序列的長度[14]。
4 實 驗
4.1 實驗目的和實驗環境
為了驗證文中提出的基于關鍵點的線性降維算法與描述統計模型相結合的實際效果，選取了10個不同領域的時間序列數據集進行實驗。實驗以壓縮率和擬合誤差作為評價優劣的指標，將MME-KP算法與PAA算法以及PLR-FP算法進行對比。
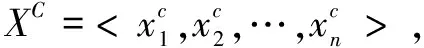
(3)
擬合誤差是用來衡量擬合時間序列與原始時間序列差異性的一個重要指標。在同等壓縮率的情況下，擬合誤差越小，表示擬合效果越好，擬合數據越接近真實數據。
4.2 實驗數據處理
確定時間序列是一組按時間先后順序排列的精確數據，這些數據通過加入擾動成為不確定化數據，由此成為不確定時間序列。給定某一時刻i，不確定時間序列在該時刻的值可表示為：
Vi=di+ei
(4)
其中，di為確定時間序列i時刻的精確值；ei為該時刻誤差，通常服從某種概率分布。
文中實驗數據取自于www.cs.ucr.edu/～eamonn/tutorials.html公布的用于數據挖掘的通用實驗數據集(KP-Data)，如表1所示。將每個數據集的訓練子集和測試子集重新配置整合，獲得實驗數據集。同時，通過不確定化模型將不確定性引入到確定序列中，人為加入擾動形成誤差ei，并使ei服從某種分布，從而將序列轉化成不確定時間序列。
表1 KP-Data數據集
4.3 實驗方法
實驗主要分為兩部分：
(1)將原始數據進行統計模型建模，每種類型的數據將分別建模得到三條確定時間序列數據：最大值序列、最小值序列和集中趨勢序列；
(2)在步驟1建立的模型基礎上，分別用提出的MME-KP算法、Yi和Keogh提出的分段聚集近似(PAA)線性表示方法，以及文獻[9]提出的PLR-FP線性表示方法對數據分別進行處理，得到整個不確定時序數據集的關鍵點集合。最終以同種壓縮率的標準下擬合誤差的大小作為評估算法質量的指標。擬合誤差越小，算法性能越好。
4.4 實驗結果與分析
(1)第一部分。
在提出的統計模型下，部分數據的建模表示如圖2所示。
(a)Fish原始數據圖
(b)StarLightCurves原始數據圖
(2)第二部分。
文中提出的MME-KP需要輸入3個閾值參數：C1、C2和C3，分別對應三條確定時間序列，即最大值時間序列、最小值時間序列及集中趨勢時間序列的關鍵點閾值參數。參數設置越大，數據的壓縮率越小，擬合誤差越大；參數設置越小，數據壓縮率越大，數據分段越精細，擬合誤差越小。實驗選取的數據來自10個不同領域，數據的差異性較大。為了對比實驗的公平性，將根據不同數據類型調整參數，保證在10組數據的壓縮率都在50%的基準下，進行三種算法的擬合誤差對比。在同一壓縮率情況下，擬合誤差越小，算法性能越好。
部分實驗結果如圖3所示。
從圖3中可以看出，在10個通用時間序列數據集中，MME-KP算法在其中7個數據集上Max-Line擬合序列的誤差最小，在另外三個數據集中，誤差與最好的算法相當。同時，由圖(b)可以看出，在EV-Line上的擬合誤差，MME-KP算法明顯優于其他兩種算法，在10個數據集中都保持優勢。實驗結果說明，采用了極值點與轉折點相結合的選取關鍵點算法，在數據降維上具有明顯優勢。因為其在保留了極值點這一數據的明顯特征外，還適當選取了體現數據特征的轉折點，減小了一些重要點被粗暴舍棄的概率，提高了數據選取的精細度，從而降低了擬合誤差。
(a)三種算法在Max-Line上擬合誤差的比較
(b)三種算法在ME-Line上擬合誤差的比較
同時實驗結果顯示：對于短時間內波動頻率比較平緩的時間序列，MME-KP算法的實驗效果與其他兩種算法相比，優勢并不是很大，如圖4中的對比1所示，MME-KP算法和PAA算法都能較好地擬合MALLAT的原始數據。但是對于短時間內波動頻率劇烈的時間序列，如圖4中的對比2所示，數據在短時間內波動較大，MME-KP算法的擬合效果就遠勝于PAA算法。主要原因是，在短時間內，時間序列波動較大，會產生大量極值點，對于以找極值點和轉折點為主要關鍵點的MME-KP算法來說會捕獲大量關鍵點，從而保證了數據主要特征的不流失。而對于PAA算法，它主要思想是以一段時間內的數據均值來代替這段序列，所以，在短時間內時間序列波動較大的情況下，在這段時間內的數據均值波動并不會很大，相對地，它的擬合序列與原序列相比，就會丟失很多重要點信息，造成擬合誤差較大。
綜上，MME-KP降維方法在與提出的描述統計模型的結合上，有以下幾點優勢：在降維效果上，可以通過參數的改變，進行不同壓縮率的降維。參數設置越高，數據壓縮程度越大。在現實應用中可以根據實際需求選擇所需的降維效果；在與其他線性降維方法PAA以及PLR-FP的比較過程中，MME-KP方法體現出了更為良好的擬合效果，誤差更小，與原始數據保持高度的一致性。
圖4 實驗對比
5 結束語
針對不確定時序數據區別于確定時序數據的主要特征，首先提出不確定時間序列向確定時間序列歸約的描述統計模型，同時綜合考慮已有的確定時間序列的線性分段思想，提出綜合考慮極值點與轉折點的關鍵點選取算法。綜合以上兩點，將不確定時序數據進行空間和時間上的有效降維。實驗結果表明，該算法在數據降維效果上有良好的性能，且能高度還原原始數據。下一步的研究工作是在所提出模型的基礎上找到更合適的原始數據擬合方案。
猜你喜歡
中學生數理化·中考版(2022年12期)2022-02-16 07:36:56
今日農業(2021年8期)2021-11-28 05:07:50
兒童故事畫報(2019年5期)2019-05-26 14:26:14
河南畜牧獸醫(2016年24期)2016-11-29 01:28:30
Coco薇(2016年2期)2016-03-22 02:42:52
Coco薇(2015年1期)2015-08-13 02:47:34
小雪花·成長指南(2015年7期)2015-08-11 15:03:12
小雪花·成長指南(2015年4期)2015-05-19 14:47:56
中國衛生(2014年2期)2014-11-12 13:00:16
語文知識(2014年7期)2014-02-28 22:00:26
