小球在圓弧軌道上滾動與滑動的對比分析

趙清鋒

(武漢市卓刀泉中學建和分校，湖北 武漢 430065)

簡諧運動一直是物理競賽中的熱點考題.在第34屆全國中學生物理競賽預賽試題的第6、16兩題,以及復賽理論試題的第一題都考察了簡諧運動的情況,而圓弧軌道上的簡諧運動又是考察的重點．同時圓弧軌道上的簡諧運動以及相關動力學特性也是大學理論物理學習的重點.基于此本文借助圓弧軌道,針對均質小球無摩擦滑動和無滑滾動問題的振動周期進行分析.首先應用動力學特性求出兩種情況小球運動的微分方程,并給出平衡位置微振動的周期;然后從機械能守恒角度對以上兩種情況進行比較分析,發現無滑滾動周期可以直接借助無摩擦滑動得到;最后將相關結論應用于競賽題中的圓柱滾動問題．

1 基本模型及兩種情況微振動周期

圖1

一個半徑為r、質量為m的均質實心圓球被置于一個半徑為R的固定圓筒中,圓筒的中心軸水平,橫截面如圖1所示.θ為某時刻小球質心到圓筒中心軸的垂線與豎直方向的夾角,兩種情況下小球都受到重力mg和支持力FN.考慮兩種情況下小球在其平衡位置的微振動周期.

(1) 小球無摩擦滑動.

考慮小球質心的運動,由牛頓第二定律可得

-mgsinθ=ma，

聯立以上兩式，化簡即可得到微分方程

由小角近似sinθ≈θ,代入(1)式可得小球無摩擦滑動對應微振動周期

(2) 小球無滑滾動.

此時小球除了受到重力mg和支持力FN以外,還受到圓筒對其的靜摩擦力f,考慮小球質心運動,由牛頓運動定理得

f-mgsinθ=ma.

(3)

由于小球與圓柱之間為無滑滾動,小球轉過角度θ1(規定小球在最低點時θ1=0)與θ之間的關系為

Rθ=r(θ+θ1).

(4)

由(4)式可得a與θ的關系為

考慮小球繞過其球心且平行于圓筒的軸轉動,由轉動定理得

其中I為小球繞過其球心軸的轉動慣量

由(3)～(7)式可得無滑滾動小球在圓弧軌道上運動的微分方程

由小角近似sinθ≈θ,代入(8)式可得小球無滑滾動對應微振動周期

2 能量角度對以上兩種情況的對比分析

分析以上兩種情況,無摩擦滑動和無滑滾動均沒有機械能損失,但從計算的微振動周期結果看T2>T1,即無滑滾動時周期更長,分析原因在于無滑滾動中滾動動能取代了部分平動動能,而總的機械能守恒,從而使質心平動速度慢一些導致運動周期更長．

設兩種情況下小球初始時與豎直方向的夾角都為θ0,當小球運動到θ位置時,對無摩擦滑動應用機械能守恒定律有

對無滑滾動應用機械能守恒有

小球繞過其質心的軸轉動對應的轉動慣量和角速度分別為

將(12)式代入(11)式,用平動動能取代轉動動能,化簡可得

比較(10)、(13)兩式可得

上式即表示在任意相同的位置,兩種情況所對應小球的速度之比為上述結果,且小球經歷的路徑相同,根據運動規律

∑si=∑viti，

(15)

可得兩種情況下小球微振動周期之比為

這與(2)、(9)所對應的結果一致．

上文中(2)式這一結果在很多文獻中有所研究,[1,2]教科書中也將其作為經典模型講解．[3]一般情況下可以將(2)式對應結果直接使用,然后在借助能量分析計算其他模型與無摩擦滑動速度的比值,從而得到周期的比值關系,進而得到其他模型的周期．

3 能量守恒分析圓柱模型的周期

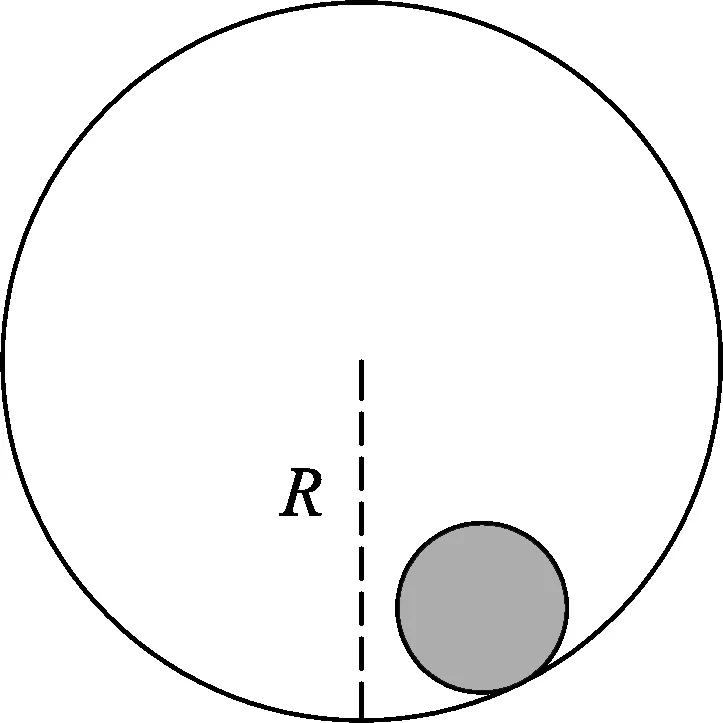
圖2

例.(第34屆全國中學生物理競賽復賽理論考試第一題)一個半徑為r、質量為m的均質實心小圓柱被置于一個半徑為R、質量為M的薄圓筒中,圓筒和小圓柱的中心軸均水平,橫截面如圖2所示．重力加速度為g．圓筒固定,小圓柱在圓筒內底部附近做無滑滾動,求小圓柱質心在其平衡位置附近做微振動的頻率．(原題有兩問,本題只分析第1問).

解析:能量守恒方法.

設初始時小圓柱質心在其橫截面上到圓筒中心軸的垂線與豎直方向夾角為θ0,當小球運動到θ位置時,對小圓柱應用機械能守恒定律有

小圓柱繞過其質心的軸轉動對應的轉動慣量和角速度分別為

將(18)式代入(17)式,用平動動能取代轉動動能,化簡可得

比較(10)、(19)兩式可以得到

此即表示在任意相同的位置,兩種情況所對應速度之比為上述結果,結合(15)式,可得兩種情況下小球微振動周期之比為

代入(4)式結果即可得到小圓柱質心在其平衡位置附近做微振動的周期和頻率為

與原題結果一致．