模擬退火法在水庫(kù)地震定位中的應(yīng)用
張聰聰 趙 杰 張亞敏
(1.山西省地震局臨汾中心地震臺(tái),山西 臨汾 041000; 2.山西省地震局應(yīng)急中心,山西 太原 030012)
1 概述
模擬退火法是一種啟發(fā)式的蒙特卡洛非線性反演方法[1],它模擬退火的物理過程:物質(zhì)先加熱融化,然后慢慢冷卻,最后達(dá)到能量最小的晶體狀態(tài)。模擬退火反演算法與傳統(tǒng)的線性反演方法相比該方法具有:不依賴初始模型的選擇、能尋找全局最小點(diǎn)而不陷入局部極小、在反演過程中不用計(jì)算雅克比偏導(dǎo)數(shù)矩陣等優(yōu)點(diǎn), 因而在地球物理資料非線性反演中受到廣泛的應(yīng)用。
2 問題描述
某水庫(kù)發(fā)生淺源地震,其坐標(biāo)為(x,y,h),在其附近有9個(gè)觀測(cè)臺(tái)站,其坐標(biāo)為(xk,yk,hk)觀測(cè)到了直達(dá)波P的走時(shí)tpk,地面水平,地球介質(zhì)均勻,發(fā)震時(shí)刻為t,P波速度vp,則存在下面的方程:
現(xiàn)在我們需要求出該地震發(fā)震位置與發(fā)震時(shí)刻(x,y,h,t),其中9個(gè)臺(tái)站坐標(biāo)與地震到時(shí)數(shù)據(jù)[2]見表1,假定vp=2 000 m/s。

表1 臺(tái)站位置坐標(biāo)及地震到時(shí)
3 模擬退火法計(jì)算(MSA)
3.1 模擬退火法步驟[3]
1)給定模型每一個(gè)參數(shù)變化范圍,在這個(gè)范圍內(nèi)隨機(jī)選擇一個(gè)初始模型m0,并計(jì)算相應(yīng)的目標(biāo)函數(shù)值E(m0);
2)對(duì)當(dāng)前的模型進(jìn)行擾動(dòng)產(chǎn)生一個(gè)新模型m,計(jì)算相應(yīng)的目標(biāo)函數(shù)值E(m),得到ΔE=E(m)-E(m0);
3)若ΔE<0,則新模型被接受,若ΔE>0,則新模型m按概率P=exp(-ΔE/kT)進(jìn)行接受,其中,k為一個(gè)常數(shù);exp為自然指數(shù);T為溫度。因?yàn)镻(ΔE)的函數(shù)取值范圍是(0,1),在0~1之間隨機(jī)產(chǎn)生一個(gè)數(shù)R,當(dāng)P(ΔE)>R時(shí),接受修改,即m0=m;
4)在溫度T下,重復(fù)一定次數(shù)的擾動(dòng)和接受過程,即重復(fù)步驟2),步驟3);
5)緩慢降低溫度T,Tnew=(0.99)k×T;
6)重復(fù)步驟2)~步驟5),直至收斂條件滿足為止。
3.2 重要參數(shù)
3.2.1溫度及下降速率
溫度T在模擬退火反演中是最重要的問題,由接受概率公式可知P=exp(-ΔE/kT),溫度實(shí)際上是一種非線性加權(quán)[3]。初始溫度T太高會(huì)增加計(jì)算時(shí)間;T也不能取太小,否則不能遍歷模型空間。收斂閾值Tm不能取太大,這樣會(huì)達(dá)不到收斂狀態(tài);Tm也不能太小,這樣會(huì)增加計(jì)算量。下降速率如果太快,雖然運(yùn)算速度快,但容易陷入局部最優(yōu)解;下降速率太慢,則運(yùn)行效率較低。
本文選擇雙曲線下降行作為退火機(jī)制,且初始選擇較高初始溫度100,選擇較低收斂溫度0.000 01,下降速率0.99。通過matlab選擇較好的參數(shù)。
3.2.2擾動(dòng)函數(shù)的選擇[4]
本文主要分析三種模型擾動(dòng)方法:
1)全局?jǐn)_動(dòng):
X′=xmin+(xmax-xmin) ×R。
其中,X′為模型新值;R為0~1之間的隨機(jī)數(shù)。
2)Ingher提出的VFSA方法:
X′=x+(xmax-xmin) ×yi;
yi=T×sign(R-0.5)×[(1+1/Tk)|2R-1|-1]。
其中,yi為擾動(dòng)因子;T為溫度;X′為模型新值;x為模型舊值;R為0~1之間的隨機(jī)數(shù)。
3)和溫度相關(guān)的局部收斂加強(qiáng)型:
u=T×tan[pi×(R-0.5)];
X′=u×(xmax-xmin)+x。
其中,u為擾動(dòng)因子;T為溫度;X′為模型新值;x為模型舊值;R為0~1之間隨機(jī)數(shù)。
4 重要參數(shù)選擇
4.1 溫度
取不同的初始溫度,收斂閾值Tm=0.000 001,下降速率k=0.99,得到的地震定位見表2,圖1為不同起始溫度到時(shí)殘差。

表2 不同初始溫度對(duì)反演結(jié)果的影響
由表2,圖1可知不同起始溫度對(duì)數(shù)據(jù)觀測(cè)值影響不大,會(huì)影響到迭代次數(shù),根據(jù)接受概率公式P=exp(-ΔE/T)可知初始溫度T的選擇應(yīng)該與ΔE同一數(shù)量級(jí)或者高一兩個(gè)數(shù)量級(jí)為宜,這樣才能更好的實(shí)現(xiàn)全局搜索,且有較高工作效率。T初始值選取,可以通過查看T取較高值時(shí)ΔE的曲線圖的縱坐標(biāo)可得。如圖2所示,迭代次數(shù)取1 000左右較為合適,即T取1或者10較適宜。為了提高搜索效率,本次采用T=1作為初始溫度。

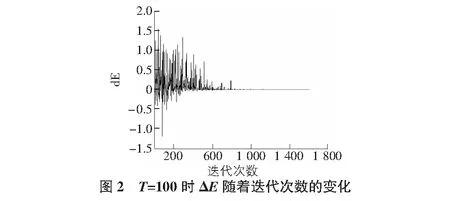
表3 不同的收斂溫度對(duì)地震反演結(jié)果的影響

T=1k=0.99迭代次數(shù)發(fā)震位置與發(fā)震時(shí)刻(x,y,h,t)xyhtTm=0.01460Tm=0.001689Tm=0.000 00191817.7734.92-200.370.474 69.2727.28-208.520.470 825.3615.67-210.240.473 541.0339.12-200.540.474 537.2437.52-203.790.472 939.2138.56-200.890.473 039.6241.62-199.980.473 739.6641.44-200.000.473 739.5641.54-199.990.473 7
由表3,圖3可知,當(dāng)初始溫度選擇T=100,下降速率為0.99時(shí),隨著溫度閾值的減小,迭代次數(shù)的增加,反演結(jié)果越來(lái)越穩(wěn)定,且到時(shí)殘差越來(lái)越小,精度越來(lái)越高。此次實(shí)驗(yàn)為了較高的反演精度選擇Tm=0.000 000 1。為了更好的全局收斂,選擇較低的降溫系數(shù)。本次實(shí)驗(yàn)選擇T=1,k=0.99,Tm=0.000 000 1 。
4.2 三種擾動(dòng)方式分析

表4 三種數(shù)據(jù)擾動(dòng)方式反演結(jié)果
由表4可知,全局?jǐn)_動(dòng)方法收斂性較差,其余兩種方法收斂性較好。圖4,圖5為具有較強(qiáng)的局部收斂性擾動(dòng)函數(shù)的擾動(dòng)因子收斂圖,溫度為T=100到Tm=0.000 000 1(下降速率0.99),從圖4可以看出該擾動(dòng)因子可以較好的收斂,且擾動(dòng)范圍大,迭代次數(shù)少,效率較高。從圖5可以看出該擾動(dòng)方法可以收斂,但是需要較多的迭代次數(shù),且擾動(dòng)范圍較小。雖然第二種方式擾動(dòng)較大,但根據(jù)公式可知很多擾動(dòng)為無(wú)效擾動(dòng),第三種方式基本全部為有效擾動(dòng)。綜上所述:
全局性:method 1>method 3>method 2;
收斂速度:method 2>method 3>method 1;
綜合考慮,選擇收斂性較強(qiáng)的method 2。

根據(jù)試驗(yàn),采用T=1,k=0.99,Tm=0.000 000 1,收斂函數(shù)method 2對(duì)地震進(jìn)行定位,然后正演獲取臺(tái)站地震到時(shí),與實(shí)際地震到時(shí)觀測(cè)值作對(duì)比(見圖6),符合性較好,結(jié)果可以接受。

5 結(jié)論與建議
1)模擬退火法的使用需要了解先驗(yàn)?zāi)P托畔⒑鸵欢ǖ膶?shí)際工作經(jīng)驗(yàn),在經(jīng)驗(yàn)缺乏的情況下,設(shè)定高的初始溫度、大的降溫系數(shù)(0.99)、小的收斂閾值。
2)由接受函數(shù)公式P=exp(-ΔE/T)可知,模擬退火算法初始溫度太高時(shí)雖然可以在比較大的模型空間中搜索,較大概率接受較差的解,但是會(huì)增加迭代次數(shù),增加計(jì)算時(shí)間。通過計(jì)算與試驗(yàn)可知,初始溫度選取與ΔE同量級(jí)或者高一量級(jí)較為適宜,ΔE數(shù)量級(jí)可以通過在較高初始溫度下畫ΔE收斂圖,看初始幅值獲得。
3)溫度閾值越小,精度越高,但是會(huì)增加迭代次數(shù),增加計(jì)算時(shí)間。
4)擾動(dòng)函數(shù)有多種方式,根據(jù)實(shí)際情況選擇合適的擾動(dòng)方法,必要時(shí)畫出擾動(dòng)因子收斂曲線圖,判斷全局性和收斂性的情況。

