基于經驗模態分解和離散小波能量特征的地毯織機噪聲源識別

徐 洋， 盛曉偉， 李昂昂， 錢如峰， 孫志軍

(東華大學 機械工程學院， 上海 201620)

地毯織機結構復雜，噪聲源眾多，且不同的噪聲信號間存在耦合的狀況，其噪聲信號一般表現為多種復雜的瞬變非穩態信號和少數穩態信號的組合，很難從地毯織機的噪聲信號中分離出獨立分量頻率特征。目前，國內外學者對地毯織機噪聲信號識別的研究較少。尤其是在國內，地毯織機噪聲研究工作起步較晚，基礎薄弱，對地毯織機噪聲源的定位識別及噪聲控制的應用研究仍停留在非常原始的階段：陳瑞琪等[1]通過對4種典型紡織機械的分析，較為全面地綜述了紡織機械噪聲產生的原因及噪聲測試方法；霍本方[2]介紹了細長型紡織機械噪聲測試方法的選用及測試經驗，解釋了如何用傳聲器來進行紡織機械噪聲測量；因此，迫切需要一種可對地毯織機噪聲進行準確識別及定位的方法，為未來地毯織機有源噪聲控制器的設計提供理論與實踐依據。

經驗模態分解(EMD)[3]能自適應地將信號按其內在特性分解成一系列本征模態分量(IMF)，但由于是在信號時域進行的分解，無法得到信號的頻域特征，且采用經驗模態分解對信號進行分解時易出現模態混疊和過分解的情況。連續小波變換(CWT)[4]是一種變分辨率的時頻分析方法，具有較好的時頻定位特性，提供了時域和頻域同時局部化的自適應時頻分析方法，但是連續小波變換將一維信號映射到二維的尺度平面上，存在大量的冗余信息。離散小波變換 (DWT)[4]通過將尺度參數和位移參數離散化，有效地解決了這個問題，不僅在數學領域取得了豐碩的成果，而且在機器視覺[5]、圖像壓縮[6]、邊緣檢測[7]、語音識別[8]以及神經網絡技術[9]等學科領域中獲得了廣泛的應用。

本文將經驗模態分解和離散小波變換方法引入到紡織機械領域，以地毯織機為對象，對織機的主要噪聲源進行定位識別，確定各主要噪聲源頻段范圍及發生部位，為地毯織機低頻噪聲源的有源消聲提供先驗數據。該方法結合了經驗模態分解和離散小波變換的優點，實現了對地毯織機噪聲信號的識別以及對主要噪聲源所在部件的定位。

1 算法基本原理

本文組合算法結合了EMD分解算法自適應分解的優點和離散小波變換處理信號能量分布的優點。具體步驟如下。

1)對給定信號x(t)，利用3次樣條插值法得到極大極小值包絡，求均值得到均值包絡曲線m(t)，將x(t)減去m(t)得到的差值記為

f(t)=x(t)-m(t)

(1)

2)判斷f(t)是否滿足IMF分量的2個條件：若不滿足，則將f(t)作為新的給定信號重復步驟1)，將滿足條件的f(t)記為c1(t)，即為第1個固有模態分量IMF1。

3)對剩余分量進行重復分解得到其余的IMF分量ci(t)，直至余量為單調函數，記為r(t)，共有n個ImF分量。此時給定信號x(t)可表示為

(2)

4)計算給定信號與各IMF分量的互相關系數，剔除虛假分量并重構信號x(t)。

5)通過能量分布法[10]確定最優分解層數m，利用離散小波變換方法進行信號分解，得到各分量小波系數。地毯織機噪聲信號x(t)在2j分辨率逼近下的低頻部分Ajf(t)和高頻部分Djf(t)可由下式推導[11]：

(3)

(4)

式中：φj,k(t)為2j分辨率下的尺度函數；ψj,k(t)為小波函數；cj,k為2j分辨率下的尺度系數；dj,k為小波系數；j為分解層數，j=1,2,…，m；k為平移指標。

對應的快速正交小波變換算法(Mallat算法)[11]為：

(5)

(6)

式中：h和g分別是正交鏡像濾波器的單位脈沖響應；n∈Z，Z為整數。

6)計算噪聲信號各分量的能量百分比，確定主要噪聲源分量。由多分辨率分解原理可知，地毯織機噪聲信號經m層分解后，其信號可表示為

(7)

式中：Am為第m層逼近分量；Di為第i層細節分量。

設地毯織機噪聲信號在各高頻部分的能量為Edi，在低頻部分的能量為Ea，其總能量為Etotal，則：

(8)

(9)

(10)

則地毯織機噪聲信號在高頻部分和低頻部分的能量百分比分別為：

(11)

(12)

7)確定主要噪聲源分量，對主要噪聲源分量進行時頻分析，并與振動信號進行對比分析，確定主要噪聲源所在部件。

2 地毯織機噪聲信號分析

2.1 地毯織機噪聲信號EMD分解

根據GB/T 7111.6—2002《紡織機械噪聲測試規范 第6部分：織造機械》，在紡織工人工作區域布置測試點，測試點距離地毯織機1 m，高度1.6 m，采樣頻率為51 200 Hz，電動機轉速為360 r/min。對采樣得到的數據進行處理后得到信號時域圖如圖1所示。

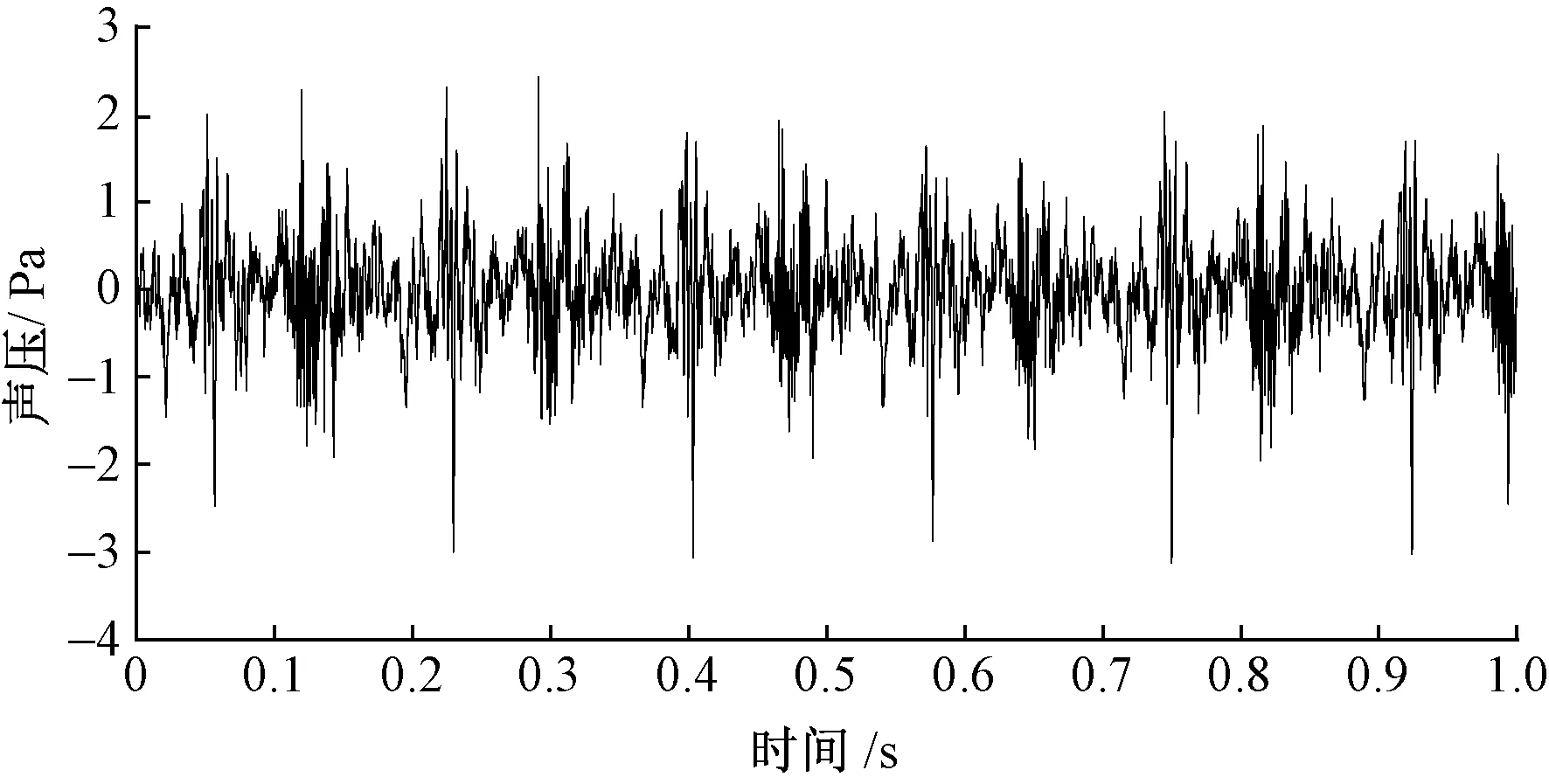
圖1 噪聲信號時域圖Fig.1 Time domain map of noise signal

從圖1可知，地毯織機噪聲信號整體表現為非穩態信號，具有明顯的沖擊特征，每秒約有6次明顯的沖擊。經聲壓轉換后發現，其主要噪聲集中在 85～95 dB之間，而這部分噪聲遠遠超過了2013年國家新修訂的GB/T 50087—2013《工業企業噪聲控制設計規范》中規定的生產車間噪聲限值85 dB。

經EMD分解后地毯織機噪聲信號按頻率從高到低分解為10個IMF分量和1個殘余分量，且分離過程中各分量之間無模態混疊現象。

2.2 優勢分量確定及信號重構

由于原始信號的信號特征僅體現在特定的幾個IMF分量中，且存在一定的虛假分量，因而有必要篩選剔除虛假分量，保留優勢分量。互相關函數是判斷信號之間相關程度的一個指標，將其歸一化得到互相關系數可剔除虛假分量。地毯織機各IMF分量與原始信號的互相關系數如表1所示。

一般情況下，互相關系數大于0.1即認為2個信號之間相關性較好[12]，故將IMF8～IMF10作為虛假分量剔除。對優勢分量IMF1～IMF7進行重構，得到地毯織機重構信號。

表1 各IMF分量與原始信號的互相關系數Tab.1 Cross correlation coefficients between IMF components and original signal

2.3 最優分解層數確定

由于小波逼近部分和細節部分分別代表了信號的高頻特性和低頻特性，且每層分解的逼近部分和細節部分能量不同，故采用能量分布法確定最優分解層數m。其主要步驟為：

1)根據采樣點數N確定最大分解層數m；

2)對信號進行最大尺度分解，得到每層小波細節系數的能量Edi(i=1,2,…，m)；

3)對小波按尺度i進行分解，在每個尺度下計算小波逼近系數的能量Eai(i=1,2,…，m)；

4)計算能量系數Ki=Edi/Eai。

分析得到m=9。根據最大分解層數進一步分析得到Edi、Eai、Ki在各分解層數下的取值如表2所示。

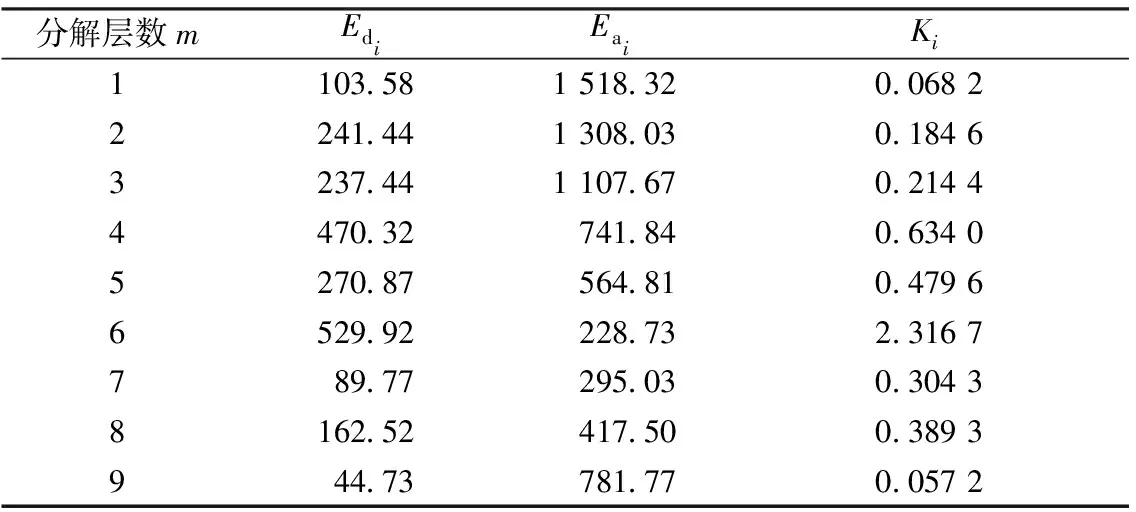
表2 各分解層數下Edi、Eai、Ki的計算結果Tab.2 Results of Edi, Eai and Ki in different layer numbers

由表2可知，當分解層數m=6時，能量系數Ki最大,故最優分解層數m=6。

2.4 離散小波變換分解重構信號

Daubechies(db)小波是工程機械中最常用的一種小波，能有效減小分解得到的各子帶數據之間的相關性，具有多階消失矩，且消失距越高，與信號做內積得到的系數越小，高頻系數越小，分解后的能量在低頻部分的集中性越好。 根據以上特性，本文選用具有20階消失矩的db20小波對重構信號進行 6層分解，各分量及其頻譜如圖2所示。

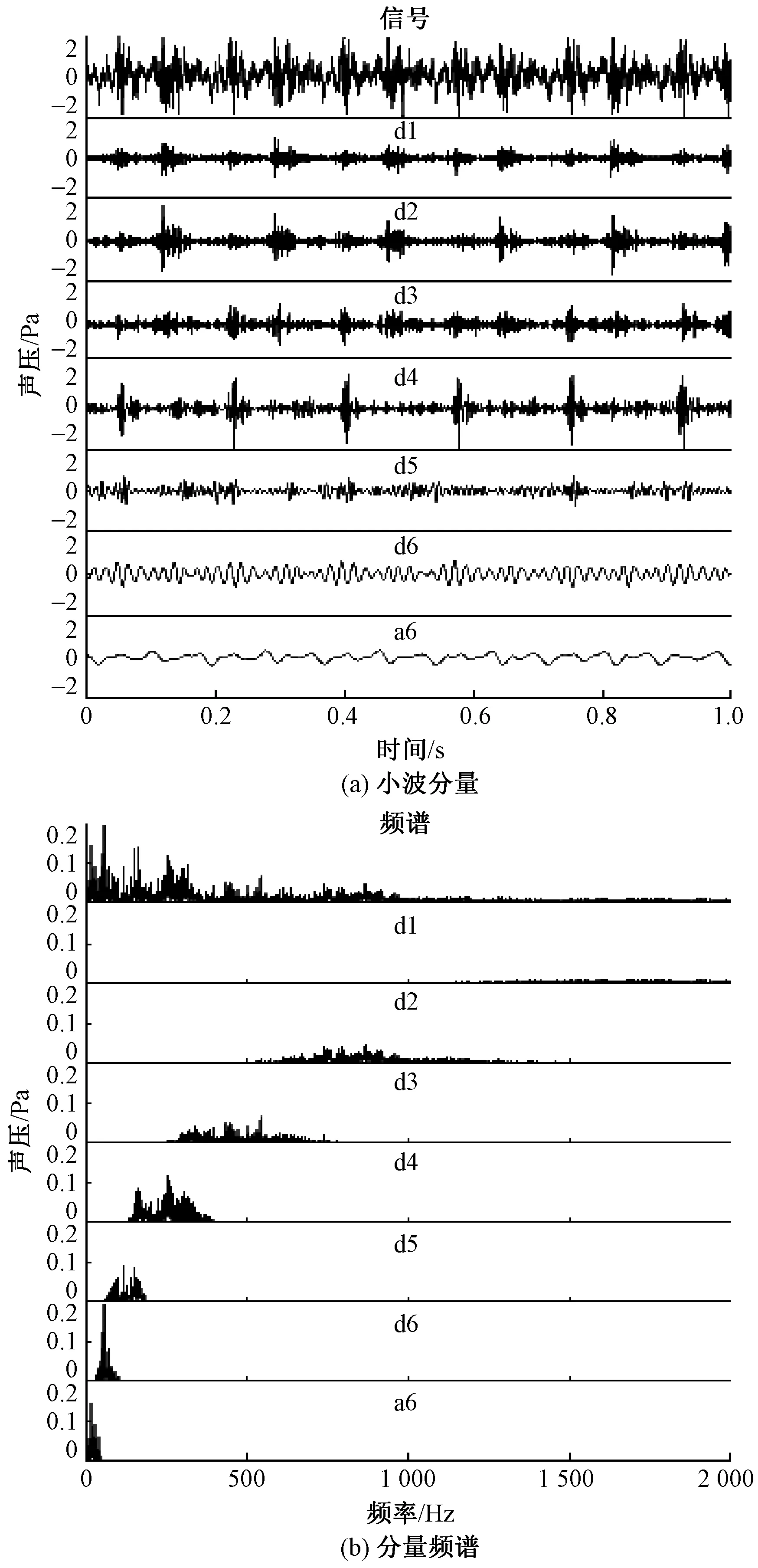
圖2 小波分量及其頻譜Fig.2 Wavelet coefficient components (a) and their spectra (b)

圖中a6表示第6階逼近系數，d1～d6表示1～6階細節系數，地毯織機噪聲信號等于第6階逼近系數與各階細節系數之和。分析可知：d1～d3分量在頻域上分布較廣，其幅值普遍較小，可認為是由傳聲器和狀態噪聲的高頻分量引起的局部干擾；d4、d5分量頻域相對較寬且幅值較大；d6分量可見明顯波峰，其最大的小波系數約為0.35；a6分量在頻域上分布較窄且其幅值較小，頻率很小，屬次聲波，人耳無法識別。

2.5 主要噪聲源的確定及分析

為準確地識別地毯織機主要噪聲源所對應的小波分量，對小波分量平方求和然后歸一化，得到各階小波分量能量占比如表3所示。可見，地毯織機噪聲各階小波能量主要集中在d4和d6這2個分量中，約占噪聲總能量的50%，為地毯織機的主要噪聲源。若能將這2個具有高能量的低頻分量消除或降低，可使地毯織機的噪聲水平直接降低10～20 dB。進一步對這2個分量進行時頻分析，采用小波基函數cmor32-1，尺寸序列長度為512，經尺度轉換后得到d4和d6的時頻圖如圖3所示(時頻圖可表示時間、頻率和幅值三者之間的關系)。結合圖2和圖3(a)分析可知，d4分量是一個沖擊信號，每秒沖擊約6次，這與電動機轉速360 r/min相符，其頻率集中于150 Hz及 250～350 Hz之間，初步判斷為地毯織機不同部件碰撞產生的沖擊噪聲；從圖3(b)可知，d6分量是一個主要頻率約為58 Hz的振動信號，初步判斷為地毯織機某一部件振動產生的頻率。

表3 各階小波分量的能量占比Tab.3 Energy ratio of wavelet coefficients %

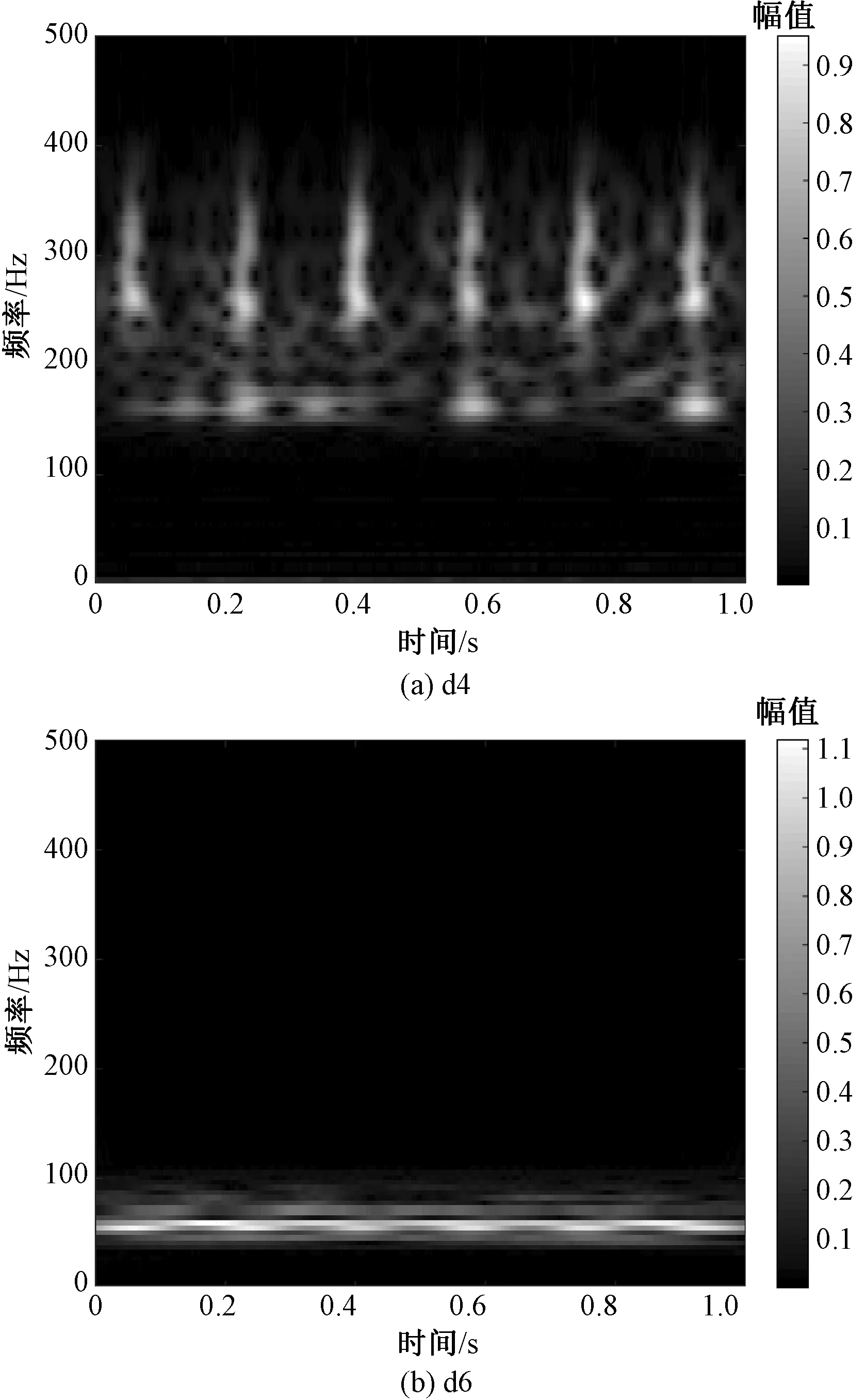
圖3 主要噪聲源時頻圖Fig.3 Spectrograms of main noise sources

3 地毯織機主要噪聲源定位

采用激光測振儀測量地毯織機主要部件的振動信號，測量距離為2.0 m，速度為50 mm/s。其現場實驗圖如圖4所示。

圖4 現場布置圖Fig.4 Experimental arrangement

實驗數據分析得到各部件的主要頻率為：鉤床6.0 Hz，分紗架 73.7 Hz，鉤從動軸6.0、57.8 Hz，壓板6.0、52.7 Hz，鉤床梳子6.0 Hz，鉤床豎軸 6.0 Hz，基座26.4 Hz，電動機主軸6.0、47.4、94.8 Hz。可以看出，鉤從動軸與壓板的主頻分別為 57.8 Hz和52.7 Hz，約為主軸轉動頻率的10倍，且與噪聲信號的d6分量頻率近似相等。鉤從動軸與壓板振動信號的相位差約為180°，在整個時間軸上恰好形成相互交替出現，特征結果見圖5。結合圖3(b)分析發現，兩振動信號的時頻圖在頻率上與d6分量的時頻圖一致，因而d6分量是鉤從動軸與壓板的振動所產生的噪聲信號。

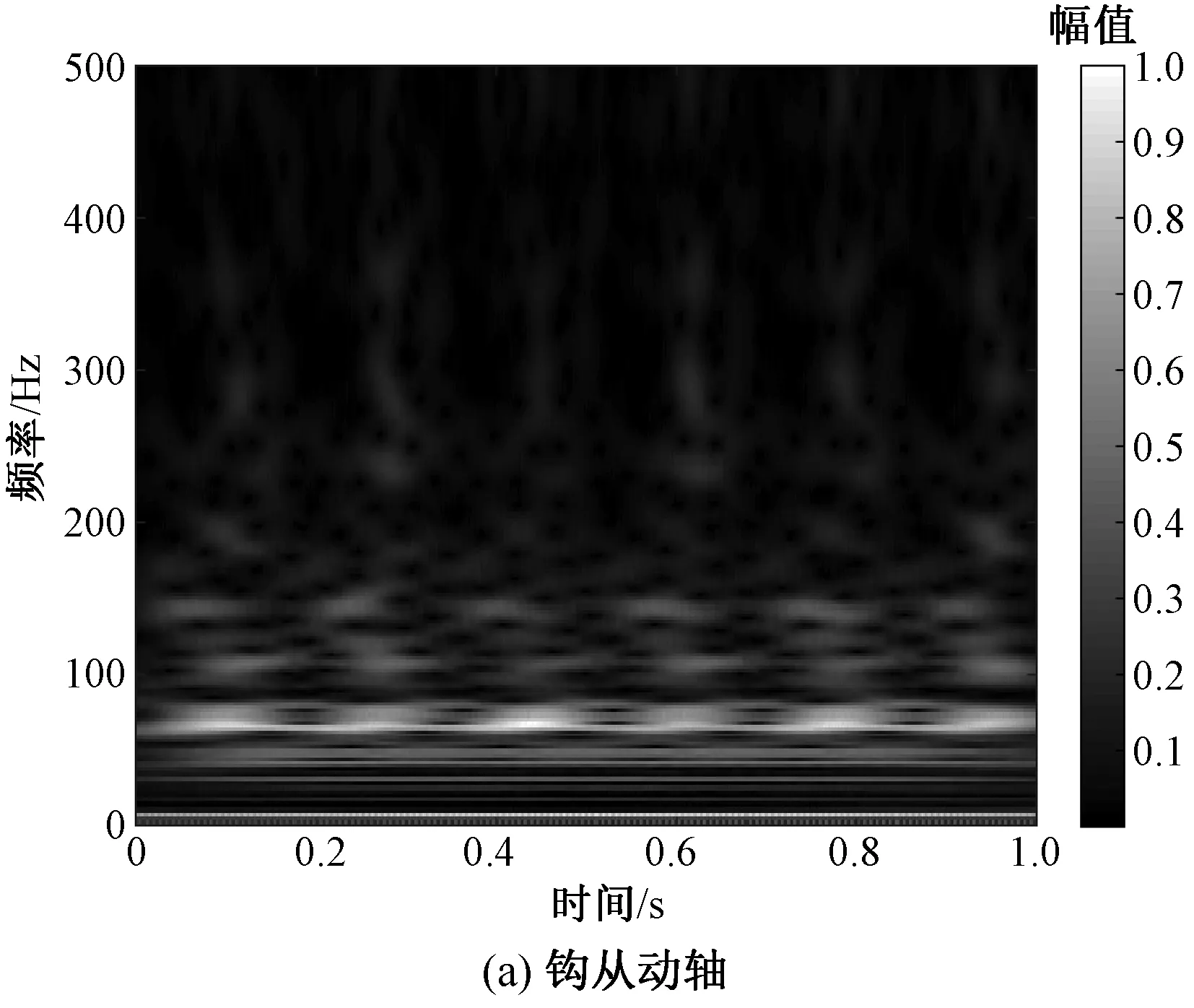
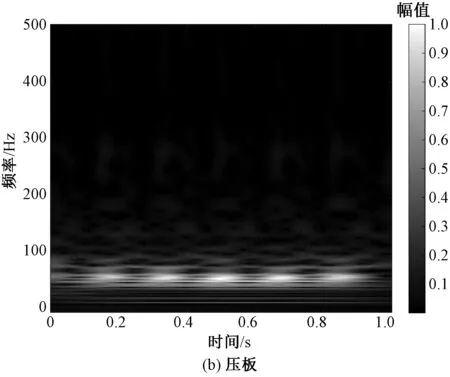
圖5 鉤從動軸和壓板時頻圖Fig.5 Spectrogram of hoolz driven draft (a) and pressing plate (b)

對鉤從動軸時域圖研究發現其信號主要表現為沖擊信號，每秒沖擊約6次，結果如圖6所示。

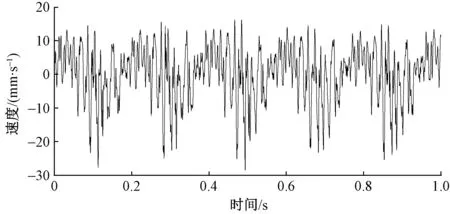
圖6 鉤從動軸時域圖Fig.6 Time domain map of a hook driven shaft

采用db20小波對鉤從動軸振動信號進行4層分解，得到各階小波系數分量如圖7所示。

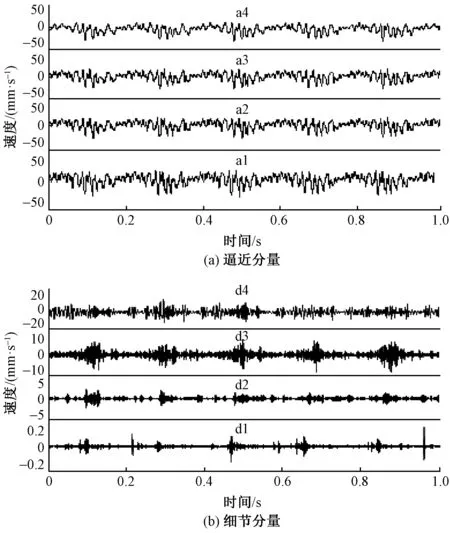
圖7 鉤從動軸小波分解圖Fig.7 Wavelet decomposition of a hook driven shaft.(a) Approximation component; (b) Details component

由圖7可知，沖擊信號主要集中在d3、d4這 2個分量中。繪制d3、d4 2個分量的時頻圖，小波基函數選用cmor32-1小波，尺寸序列長度為512，經尺度轉換后得到d3和d4的時頻圖如圖8所示。

結合圖8與圖3(a)分析發現，鉤從動軸經離散小波分解后得到的具有明顯沖擊特征的2個振動分量恰好組成了噪聲信號的d4分量，于是判斷鉤從動軸是產生沖擊信號的2部件之一。

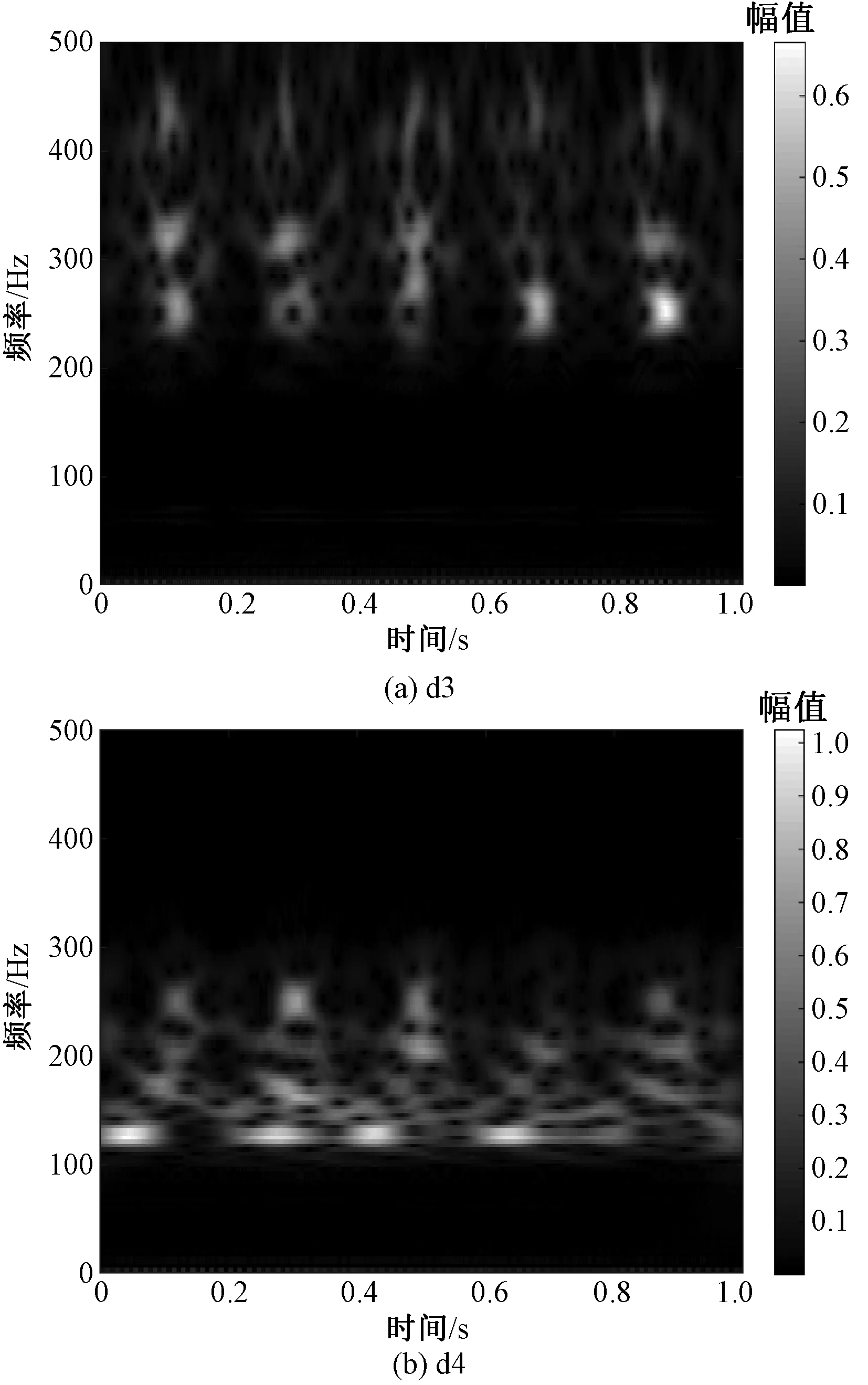
圖8 鉤從動軸沖擊分量時頻圖Fig.8 Spectrogram of a hook driven shaft’s impact component

進一步分析地毯織機結構,數千根簇絨針隨著針床傳動機構往復運動，將絨紗植入地毯底布，與此同時，與簇絨針精確配合的成圈鉤鉤住絨紗[13]。此時，針從動軸上的簇絨針與鉤從動軸上的成圈鉤碰撞產生沖擊信號，由于電動機轉速為360 r/min，故每秒產生沖擊6次。結合對地毯織機噪聲信號的分析發現，地毯織機噪聲信號的沖擊分量主要是由于簇絨針與成圈鉤的撞擊所產生的沖擊信號以及由撞擊所產生的針從動軸與鉤從動軸的振動。

4 結 論

1)簇絨地毯織機的噪聲主要集中在1 000 Hz以下，屬于中低頻噪聲，其主要組成部分為沖擊噪聲與振動噪聲。

2)本文方法能有效分解噪聲信號，可直觀地得到各分量的頻譜以及在時頻圖上的頻率分布與能量強度；Daubechies小波適用于分析簇絨地毯織機的噪聲信號；當分解層數為6時，分解效果最佳。

3)簇絨地毯織機的主要噪聲源為鉤從動軸與壓板振動產生的振動噪聲，頻率約為58 Hz；簇絨針與成圈鉤撞擊產生的沖擊噪聲，其頻率主要集中在150 Hz及250～350 Hz之間。