聯(lián)合多普勒的載波相位精密測速方法

姚 曜，張 帆，杜紅松，王 涵

（1. 中國人民解放軍91977部隊(duì)，北京 100036；2. 中國人民解放軍92981部隊(duì)，北京 100161）

目前主流的速度測量方法有慣性導(dǎo)航測速以及基于GNSS系統(tǒng)的速度測量等[1]。慣性系統(tǒng)具有自主性，但其測速存在誤差積累的問題。GNSS測速精度高，是一種理想的速度測速方法[2]。當(dāng)前GNSS測速方法主要包含位置微分測速、多普勒觀測量測速和載波相位差分等三種，這三種方法特點(diǎn)有：1）位置微分測速法是通過位置微分獲得速度的方法，優(yōu)點(diǎn)是測速方法簡單，但此方法受單點(diǎn)定位精度影響明顯，測速精度一般只有0.2 m/s，實(shí)際無法應(yīng)用在高精度測速的場合；2）多普勒測速基于衛(wèi)星和用戶間的多普勒效應(yīng)測速，優(yōu)點(diǎn)是可靠性高，而且理想的條件下測速精度可以達(dá)到2 cm/s[3]，文獻(xiàn)[4]對多普勒測速方法進(jìn)行分析測試，其中在靜態(tài)條件下多普勒測速可以達(dá)到1～2 cm/s的精度；3）載波相位測速方法優(yōu)點(diǎn)是測速精度高，目前可實(shí)現(xiàn)mm/s級別的測速精度[5]，然而該方法無法避免整周模糊度跳變的影響。通過以上分析，為了實(shí)現(xiàn)高精度測速精度，需要引入載波相位觀測量，但傳統(tǒng)的載波相位時(shí)間差分方法沒有考慮觀測噪聲以及周跳的影響，其中噪聲是影響測速精度的主要誤差源，而周跳是影響該方法測速可靠性的主要風(fēng)險(xiǎn)源之一，為了消除周跳以及降低觀測噪聲對載波相位測速法的可靠性影響，本文提出多普勒聯(lián)合載波相位的兩步精密測速方法，該方法首先通過多普勒檢測并排除周跳的影響，由此利用無周跳影響的載波相位時(shí)間差分作為觀測量，通過 Kalman濾波降低高頻噪聲的影響，使得該測速方法在滿足高精度的同時(shí)免受周跳的影響。

1 載波相位差分測速算法

載波相位是GNSS中基礎(chǔ)的觀測量，相比偽距觀測量具有更高的精度，因此被廣泛應(yīng)用在高精度領(lǐng)域。根據(jù)載波相位觀測量的特點(diǎn)，可以通過相鄰歷元時(shí)間差分的方式獲得載波相位時(shí)間差分觀測量進(jìn)行高精度速度測量。

1.1 載波相位差分測速模型

載波相位定位的原始觀測方程，

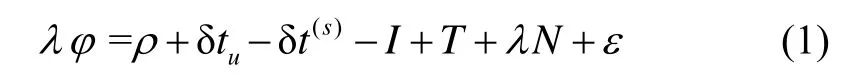
式中，l表示載波波長，j為以周為單位的載波相位觀測值，r是衛(wèi)星與接收機(jī)之間的幾何距離，δtu是接收機(jī)時(shí)鐘誤差，是衛(wèi)星時(shí)鐘誤差，I是電離層延時(shí)，T是對流層延時(shí)，N為整周模糊度，e為其余誤差[6]。

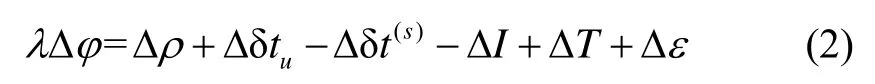
將衛(wèi)星與接收機(jī)的幾何距離變化△r用衛(wèi)星位置和接收機(jī)位置x以及觀測矢量表示，將兩個(gè)相鄰時(shí)刻位置變化線性化[8]，其中，v表示 tk-1到tk時(shí)間段的平均速度，得到測速解算方程為

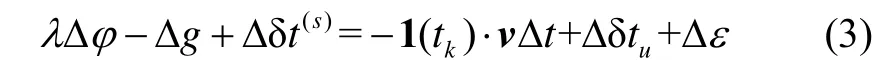
式中，△g是與衛(wèi)星和接收機(jī)位置及觀測方向矢量有關(guān)的量[9]，

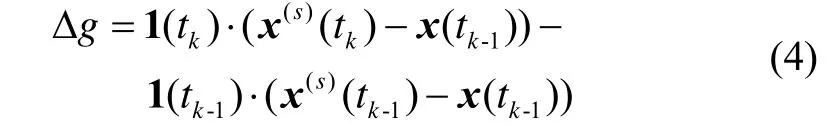
可以通過最小二乘法或Kalman濾波求解平均速度v。

Kalman濾波是一種遞推線性無偏最小方差估計(jì)方法，通過系統(tǒng)的狀態(tài)轉(zhuǎn)移方程，根據(jù)前一時(shí)刻的狀態(tài)估值和當(dāng)前時(shí)刻的觀測值遞推估計(jì)新的狀態(tài)估計(jì)值，進(jìn)而可以降低高頻噪聲的干擾。與最小二乘法相比，Kalman濾波更適合于動(dòng)態(tài)定位數(shù)據(jù)處理[10]，因此本文采用Kalman濾波解算。

在 tk時(shí)刻將隨機(jī)線性連續(xù)系統(tǒng)離散化，狀態(tài)方程：量測方程其中，時(shí)刻系統(tǒng)狀態(tài)向量，?k|k-1為狀態(tài)轉(zhuǎn)移矩陣；為觀測量與狀態(tài)量之間的量測矩陣；wk為過程噪聲向量，vk為測量噪聲向量，采用大地坐標(biāo)系WGS-84表示解算的速度值，作為狀態(tài)量。

以動(dòng)態(tài)測量為例，來說明 Kalman模型設(shè)計(jì)，其中，量測值殘差zk表示為

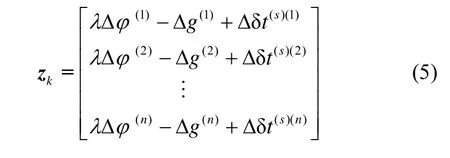
式中，n為觀測衛(wèi)星數(shù)，設(shè)置狀態(tài)轉(zhuǎn)移矩陣?k|k-1和量測矩陣Hk，

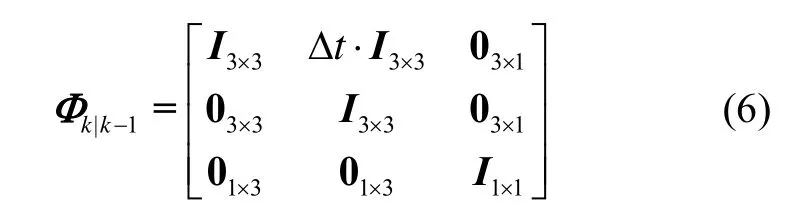
式中，I表示單位陣,Dt為采樣間隔。

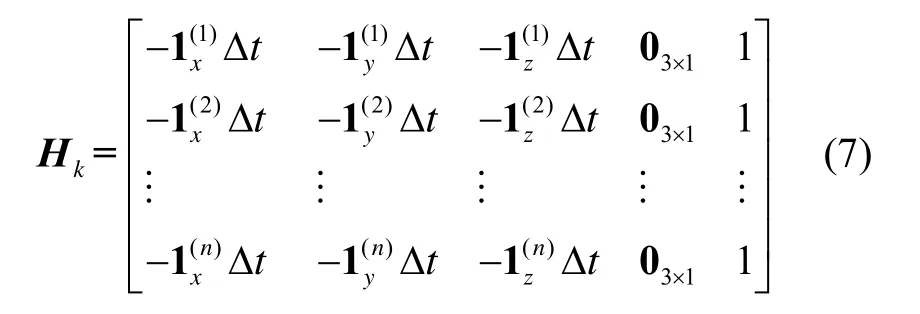
采用衛(wèi)星高度角加權(quán)模型設(shè)置測量噪聲vk協(xié)方差陣R，即：

式中，系數(shù)a為載波相位噪聲系數(shù)，根據(jù)經(jīng)驗(yàn)值，選擇系數(shù)=3mma，qi為第i衛(wèi)星高度角[11]，則量測噪聲只是衛(wèi)星高度角的函數(shù)，由于時(shí)間差分將會(huì)放大噪聲方差為原來的2倍，因此系數(shù)需要乘2。根據(jù)經(jīng)驗(yàn)，選擇每顆衛(wèi)星過程噪聲都服從相互獨(dú)立且均值為 0，方差為0.005的正態(tài)分布，即

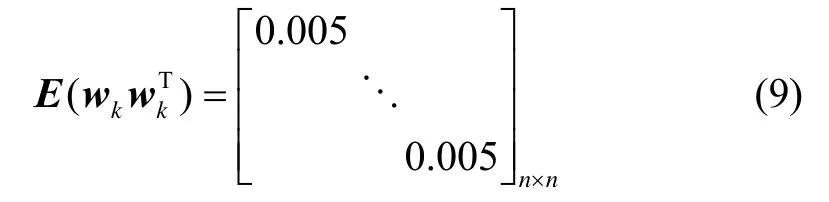
設(shè)后驗(yàn)均方誤差陣Pk初始值為主對角線100的7階方陣，并通過Kalman濾波預(yù)測過程進(jìn)行迭代更新。通過 Kalman濾波的預(yù)測和校正遞推過程，可以解得速度狀態(tài)量

1.2 聯(lián)合多普勒周跳檢測方法

當(dāng)接收機(jī)在對載波相位觀測量進(jìn)行連續(xù)觀察時(shí)，若追蹤環(huán)路無法保持鎖定載波信號，則可能會(huì)丟失掉個(gè)整周，導(dǎo)致兩個(gè)時(shí)刻間的載波相位變化量的測得值相差了個(gè)整周期[12]。當(dāng)發(fā)生周跳時(shí)，時(shí)間差分的觀測方程改寫為

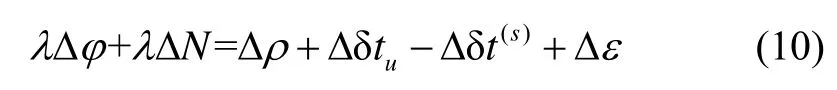
針對周跳現(xiàn)象對載波相位時(shí)間差分測速法的可靠性帶來嚴(yán)重的影響，本文提出一種聯(lián)合多普勒的載波相位精密測速方法。

設(shè)衛(wèi)星s在軌道上以速度v(s)運(yùn)行，用戶接收機(jī)以速度v運(yùn)行時(shí)，由于多普勒效應(yīng)，產(chǎn)生多普勒頻移fd=通過與載波相位時(shí)間微分方程聯(lián)立，可以得到多普勒頻移觀測量的解算方程，

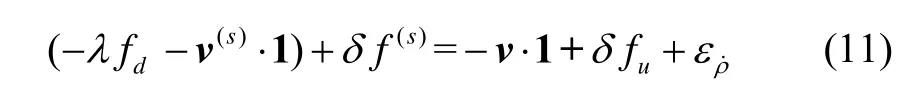
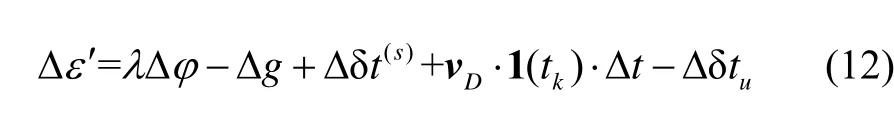
式中，vD為通過多普勒方法解算的速度，為聯(lián)合多普勒的載波相位測速方法的速度殘差量，可以用來判斷是否發(fā)生周跳，本文采用c2假設(shè)檢驗(yàn)方法。

假設(shè)n個(gè)方程殘差量服從相互獨(dú)立且均值為0，方差為s2的正態(tài)分布，SSE（Sum of Square for Error）代表速度測量殘差平方和，即則對應(yīng)的統(tǒng)計(jì)檢測量服從自由度為3n-的c2分布。在同一歷元內(nèi)觀測方程個(gè)數(shù)為n時(shí)，取c2檢驗(yàn)，

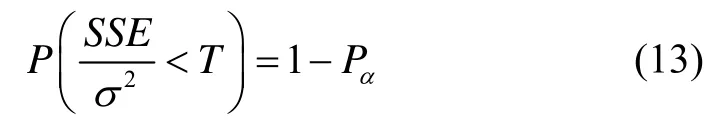
式中，Pa為拒絕檢驗(yàn)概率，可以得到門限值T，當(dāng)觀測方程不滿足上式，即拒絕假設(shè)，則該歷元出現(xiàn)周跳現(xiàn)象。

在檢測到歷元發(fā)生周跳，為了可以通過載波相位差分的方式實(shí)現(xiàn)高精度測速，需要剔除周跳衛(wèi)星觀測量，仍然可以通過其它非周跳衛(wèi)星觀測量保證該方法測速的高精度性，采用3s準(zhǔn)則對周跳歷元進(jìn)行進(jìn)一步檢測的方式。依次檢驗(yàn)出現(xiàn)周跳歷元的n個(gè)殘差值，通過多歷元標(biāo)準(zhǔn)差平均得到標(biāo)準(zhǔn)差s，設(shè)該歷元第i個(gè)殘差為再由3s準(zhǔn)則，當(dāng)檢測到即認(rèn)為該衛(wèi)星觀測方程發(fā)生周跳，需要將該受到周跳影響的觀測量剔除。

在同一歷元的n個(gè)有效衛(wèi)星中，當(dāng)沒有周跳影響的n'個(gè)衛(wèi)星數(shù)滿足可以通過本文方法精確計(jì)算接收機(jī)運(yùn)行速度；當(dāng) 4n￠時(shí)，即衛(wèi)星過少或相出現(xiàn)過多周跳衛(wèi)星，若此時(shí)總有效衛(wèi)星數(shù)n≥4，通過多普勒方法計(jì)算的速度作為該歷元速度；當(dāng)總有效衛(wèi)星數(shù) 4n時(shí)，根據(jù)衛(wèi)星導(dǎo)航定位及測速原理，無法直接計(jì)算該歷元速度。

2 實(shí)驗(yàn)測試

本文分別設(shè)計(jì)了靜態(tài)與動(dòng)態(tài)兩組測試實(shí)驗(yàn)，通過與傳統(tǒng)測速方法進(jìn)行對比，從測速精度及可靠性兩方面綜合評估所提出聯(lián)合測速法的測速性能。實(shí)驗(yàn)通過Novatel-ProPark6接收機(jī)以1Hz采樣率獲得GPS觀測數(shù)據(jù)，靜態(tài)測試采集時(shí)長1.5 h，動(dòng)態(tài)測試采集時(shí)長2 h。為了測試周跳現(xiàn)象對實(shí)驗(yàn)測試的影響，人為注入周跳以判斷該方法檢測周跳的能力。采用靜態(tài)試驗(yàn)中每10 min在1顆衛(wèi)星觀測量加2周的周跳，動(dòng)態(tài)實(shí)驗(yàn)中每10 min在1顆衛(wèi)星觀測量加5周周跳的方式。為有效評估測速算法的性能，本實(shí)驗(yàn)采用平面距離均方根（Distance Root Mean Squared, DRMS）、天向軸向均方根（Up Root Mean Squared, Up RMS）及球概率誤差SEP95（Sphere Error Probability of 95%）等三種統(tǒng)計(jì)量綜合評估算法測試速度精度及可靠性性能。

需要說明的是，由于動(dòng)態(tài)測試沒有準(zhǔn)確的測速參考，考慮到動(dòng)態(tài)測試環(huán)境為水平路面，取其天向方向上的運(yùn)動(dòng)作為誤差比較方向。而實(shí)驗(yàn)場地并不是理想水平，導(dǎo)致試驗(yàn)車處于擺動(dòng)、顛簸的狀態(tài)，使得天向速度真值不能絕對為零。

2.1 靜態(tài)測試

圖1展示了傳統(tǒng)位置微分測速法、多普勒測速法、載波相位測速法靜態(tài)測試在東向、北向和天向速度結(jié)果。

圖2展示了載波相位測速法無周跳檢測方法與多普勒檢測周跳方法在東向、北向和天向速度對比結(jié)果。

圖1 傳統(tǒng)測速方法比較Fig.1 Comparison of traditional velocity measurement methods

圖2 載波相位周跳檢測對比Fig.2 Comparison of carrier phase cycle-slips detection

表1展示了載波相位時(shí)間差分聯(lián)合多普勒法和傳統(tǒng)的位置微分法、多普勒法以及載波相位差分法測速精度對比結(jié)果。

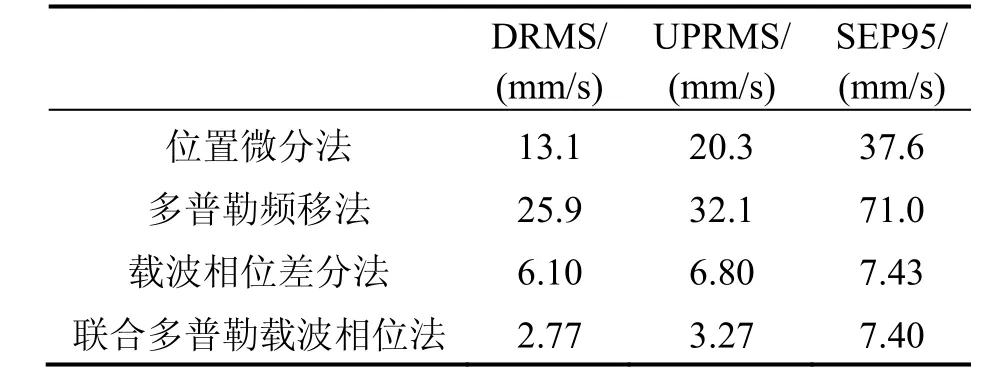
表1 載波相位時(shí)間差分聯(lián)合多普勒法與傳統(tǒng)測速方法靜態(tài)測試精度比較Tab.1 Comparison on static test precisions among the four methods

從表1可以看出，位置微分法測速誤差SEP95為3.7 cm/s，速度誤差比多普勒測速法的測速誤差7.1 cm/s降低48%，其原因是位置微分法受接收機(jī)性能影響較大，而ProPark6接收機(jī)對于偽距觀測量采用了相位平滑算法，有效提升單點(diǎn)定位精度。相比于位置微分測速、多普勒測速，相位差分法的測速精度達(dá)到7.4 mm/s，可實(shí)現(xiàn)mm/s級的測速精度需求。但是從圖1中發(fā)現(xiàn)，由于傳統(tǒng)的相位差分測速法并未考慮周跳的影響，導(dǎo)致存在多處測速異常點(diǎn)，有周跳影響下的 DRMS為6.1 mm/s。由此可見，周跳現(xiàn)象是相位差分測速法影響可靠性的主要干擾源。本文提出的一種聯(lián)合多普勒的載波相位精密測速方法，可以對周跳點(diǎn)進(jìn)行檢測并剔除。通過周跳檢測，剔除周跳衛(wèi)星，成功消除載波相位測速的全部速度異常點(diǎn)，含周跳檢測的測速誤差DRMS由6.1 mm/s降到2.8 mm/s，在滿足載波相位時(shí)間差分測速的精度下，實(shí)現(xiàn)測速的可靠性。

為了進(jìn)一步提升靜態(tài)測速性能，采用 Kalman濾波算法對觀測量的高頻噪聲進(jìn)行優(yōu)化抑制，設(shè)置測量噪聲協(xié)方差陣R，其中參數(shù)a=3 mm。圖3展示了載波相位包含周跳檢測，并分別通過最小二乘法與Kalman濾波解算結(jié)果對比。

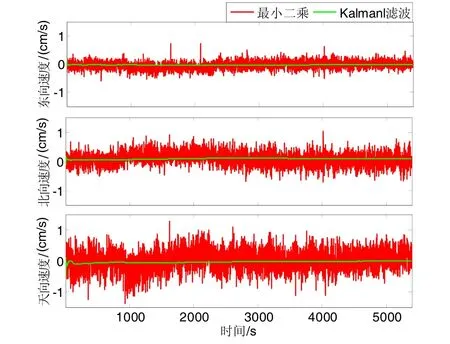
圖3 載波相位周跳檢測對比Fig.3 Comparison of carrier phase cycle-slips detection

表2展示了最小二乘法、Kalman濾波精度比較結(jié)果。由表2比較可知，在靜態(tài)試驗(yàn)中，Kalman濾波解算速度誤差SEP95由最小二乘法的7.40 mm/s下降到1.10mm/s，體現(xiàn)了 Kalman濾波在對高頻噪聲的抑制作用。

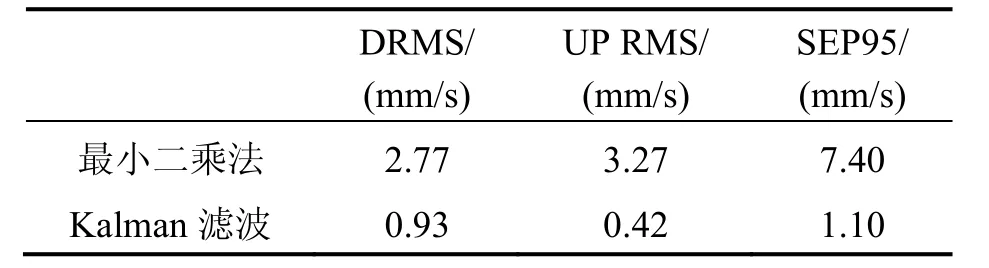
表2 最小二乘法和Kalman濾波靜態(tài)測試比較Tab.2 Compa rison on static test precisions between least square method and Kalman filter method

通過以上靜態(tài)實(shí)驗(yàn)結(jié)果比較可知：通過聯(lián)合多普勒的載波相位時(shí)間差分測速方法可以達(dá)到 mm/s級的精度，并且通過周跳檢測，消除了周跳帶來的野值影響；同時(shí)，采用 Kalman濾波方法測速精度得到了進(jìn)一步的提高。

2.2 動(dòng)態(tài)測試

車載動(dòng)態(tài)測試時(shí)間是2016年5月10日12:30～14:30，采用Novatel-ProPark6接收機(jī)以1 Hz頻率采樣，共繞哈爾濱工程大學(xué)軍工操場15圈，運(yùn)行軌跡如圖4所示。

圖4 車載動(dòng)態(tài)實(shí)驗(yàn)運(yùn)行路線Fig.4 Vehicle running route in dynamic experiment

圖5展示了動(dòng)態(tài)位置微分法、多普勒法和載波相位差分法在東向、北向和天向的測速結(jié)果，圖6展示了聯(lián)合多普勒的檢測周跳法和無周跳檢測的速度結(jié)果。

圖5 傳統(tǒng)測速方法比較Fig.5 Comparison of traditional speed measurement methods

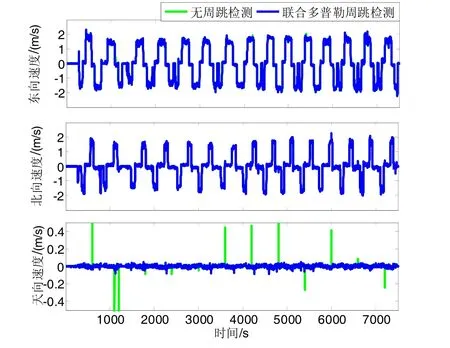
圖6 載波相位周跳檢測前后對比Fig.6 Comparison on with and without carrier phase cycle-slips detection

從圖5可知，位置微分測速方法在天向上出現(xiàn)多處達(dá)到 1 m/s的野值點(diǎn)，因此實(shí)際難以應(yīng)用在高精度場合。相比位置微分法，多普勒測速可靠性表現(xiàn)更明顯，其中在天向上測速誤差RMS為6.3 cm/s，天向95%點(diǎn)為 12 cm/s。通過傳統(tǒng)的載波相位測速方法，天向95%點(diǎn)速度誤差由多普勒測速方法的 12 cm/s下降到2.4 cm/s，然而由于多處點(diǎn)受到周跳影響，天向速度誤差RMS由多普勒測速法的6.3 cm/s擴(kuò)大到29 cm/s，可見周跳現(xiàn)象對載波相位測速可靠性產(chǎn)生很大影響。通過圖6周跳檢驗(yàn)前后對比，聯(lián)合多普勒的載波相位方法，消除了所有的周跳野值點(diǎn)，天向速度誤差RMS由無周跳檢測的29 cm/s降到1.3 cm/s。

為了進(jìn)一步提升動(dòng)態(tài)測速性能，采用 Kalman濾波算法對觀測量的高頻噪聲進(jìn)行優(yōu)化抑制。圖7展示了聯(lián)合多普勒的載波相位測速方法由 Kalman濾波法與最小二乘方法解算速度比較。

圖7 Kalman濾波法與最小二乘法比較Fig.7 Comparison between Kalman filter and least square methods

從圖7比較可知，聯(lián)合多普勒的載波相位測速方法，通過Kalman濾波解算，天向速度誤差95%點(diǎn)由最小二乘的 2.4 cm/s下降到 2.1 cm/s，天向速度誤差RMS由最小二乘的1.3 cm/s降到1.1 cm/s。從天向方向上看，Kalman濾波比最小二乘法收斂更加明顯。

圖8展示了聯(lián)合多普勒的載波相位測速方法與傳統(tǒng)多普勒法測速方法之間的比較。與聯(lián)合多普勒的載波相位測速方法相比，多普勒測速噪聲較為明顯，載波相位測速天向誤差95%點(diǎn)由多普勒測速法的12 cm/s下降到2.1 cm/s，相比多普勒方法體現(xiàn)該方法測速精度的優(yōu)越性。

圖8 聯(lián)合多普勒的載波相位法與多普勒法比較Fig.8 Comparison between “Doppler + carrier phase”method and Doppler method

3 結(jié) 論

本文提出一種聯(lián)合多普勒的載波相位精密測速方法，一方面，通過Kalman濾波降低高頻噪聲的影響，另一方面，通過與多普勒測速法聯(lián)合，檢驗(yàn)并剔除周跳的影響。最后，通過靜態(tài)和動(dòng)態(tài)試驗(yàn)測試該測速方法的精度。動(dòng)態(tài)測試中，該方法測速誤差在天向方向上95%的點(diǎn)相比多普勒測速法的12 cm/s下降到2.1 cm/s，因?yàn)閯?dòng)態(tài)實(shí)驗(yàn)路面不是理想水平，天向速度呈現(xiàn)的周期規(guī)律每圈一致，可見實(shí)際動(dòng)態(tài)測速應(yīng)該達(dá)到了優(yōu)于2 cm/s的精度，并且可以檢驗(yàn)2周的周跳。試驗(yàn)結(jié)果表明，該方法測速精度優(yōu)于傳統(tǒng)的方法，并且消除了周跳的影響，驗(yàn)證了該測速方法具有高精度同時(shí)保證了可靠性。