云平臺訪問控制自適應風險評估指標權重分配方法

楊宏宇，寧宇光

(中國民航大學計算機科學與技術學院，天津300300)

(*通信作者電子郵箱yhyxlx@hotmail.com)

0 引言

云環境下訪問控制模型通常將基于屬性的訪問控制(Attribute Based Access Control，ABAC)與基于角色的訪問控制(Role Based Access Control，RBAC)相結合［1］，為進一步分析訪問授權所帶來的安全風險和增強訪問控制模型的動態性，通過引入風險因素改進訪問控制模型已經成為目前的研究熱點［2－3］。

風險值的量化方法是風險訪問控制模型研究的重點。Cheng等［4］提出模糊多水平安全模型，將風險值量化為未授權泄露信息的期望(風險值=信息價值×未授權泄露信息的概率)。Ni等［5］提出模糊BLP(Bell-LaPadula)模型，運用模糊理論將模糊化的風險量化為具體的風險值。上述2種模型均需預先給出主客體的安全水平，但在云平臺下主客體頻繁變動，無法提前評估其安全水平，故上述2種模型不適用于云平臺。

Lakshmi等［6］提出一種適用于云平臺的多風險指標訪問控制模型，提取訪問發生的時間、位置等作為風險評估指標并將風險值量化為多個風險指標的平均值，但該模型僅為每個風險指標均分固定的權重。

在云環境下存在大量歷史用戶行為信息未得到高效利用、未評估當前系統安全狀態等問題。針對上述問題，Bouchami等［7］提出將用戶歷史行為信息和系統安全狀態量化為風險評估指標評估當前訪問請求的風險。但該研究未給出具體的風險訪問控制模型。Chen等［8］提出動態風險訪問控制模型(Dynamic Risk-based Access Control，DRAC)，利用數據流方法量化用戶歷史行為信息并結合系統安全狀態構建風險評估指標。匡亞嵐［9］提出基于系統安全風險的訪問控制模型，該模型利用模糊層次分析法為風險評估指標分配權重。但上述方法均存在風險評估指標權重固定且不能動態分配的問題。

為進一步適應云環境，目前主流風險訪問控制模型是在傳統的訪問控制策略上添加風險評估模塊［7，10］(如:DRAC)，但這些模型對訪問請求風險值量化時仍面臨風險評估指標權重分配的主觀性和靜態性問題［11］，主要原因為:

1)采用經驗或專家建議等方法構建風險評估指標權重會帶有一定程度的主觀臆斷，從而影響風險值的準確率。

2)風險評估指標權重分配后是靜態的，而對于動態的云環境，會降低風險值對訪問請求的靈敏度。

對于風險評估指標權重固定的問題，目前常用的動態權重分配方法如歸一法、主成分分析法和熵值法等均存在準確率較低或實時性較差的問題［12－13］。

針對上述問題，本文提出一個云平臺訪問控制自適應風險評估指標權重分配方法，利用系統安全狀態和用戶歷史行為信息構建風險評估指標，設計一個帶約束的多元線性回歸模型，自適應分配風險評估指標權重，通過對配方回歸(Programming Regression，PR)［14］算法改進求解相應權重，提高風險值對訪問請求的靈敏度，進而提出一個新的動態閾值計算方法，提高風險值的準確率。本文方法中，風險評估指標權重不再主觀設定而是通過歷史用戶行為信息和系統安全狀態等進行計算分配，不僅分配權重合理，而且可實時調整權重以適應當前的訪問環境。本文的研究聚焦于改進云平臺風險訪問控制模型中風險評估指標權重分配的自適應性，提出動態風險值量化公式，并不涉及云平臺動態資源調度、彈性計算和虛擬化等特點。

1 基本定義

定義1 風險閾值t為:

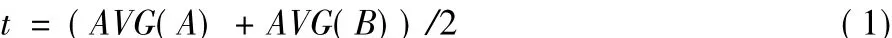
其中AVG()計算集合中訪問請求風險值的平均值。由用戶自定義計算t的訪問請求數量并將訪問請求分為A、B集合，A集合存放ABAC模塊評估接受(P=0)的訪問請求風險值R+，B集合存放ABAC模塊評估拒絕(P=1)的訪問請求風險值R－。

定義2 靈敏度S為:

其中，靈敏度S定義為P=1時訪問請求的風險平均值與P=0時訪問請求的風險平均值之差。由于靈敏度S反映風險值的波動，而風險評估指標權重影響風險值，所以靈敏度與當前風險評估指標權重密切相關。

定義3 準確率Acc為:

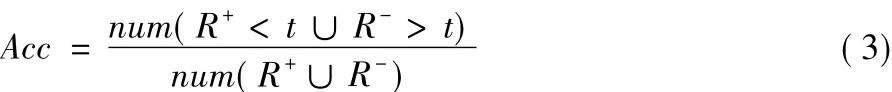
其中，num()表示滿足相應條件的訪問請求數量。準確率定義為正常訪問請求風險值R+＜t和惡意訪問請求風險值R－＞t的數量占所有訪問請求數量的比例。

定義4 風險評估指標權重b*邊界調整公式為:

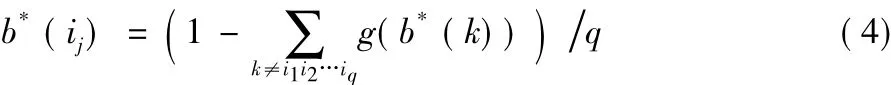
其中:b*(ij)(j=1，2，…，q且1≤i1＜i2＜… ＜iq≤p)表示b*中為0的分量;函數g()表示b*中非邊界分量的數值(小數點后保留2位)。運用配方回歸理論［14］，b*可能存在b*(ij)=0即b*在邊界 上，但任意參與風險計算的評估指標都應分配權重，故用式(4)為邊界分量分配相應值。

2 風險訪問控制模型

本文提出的風險訪問控制模型框架如圖1所示，其中，風險評估(Risk Evaluation，RE)包括自適應風險評估指標權重分配和風險值計算兩個過程。

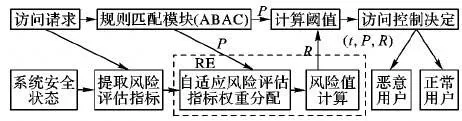
圖1 風險訪問控制模型框架Fig.1 Framework of risk access control model

該模型的處理步驟設計如下:

1)通過訪問請求和系統安全狀態提取風險評估指標。

2)規則匹配模塊利用ABAC策略與訪問請求進行規則匹配，產生匹配結果P。

3)自適應風險評估指標權重分配通過提取的歷史風險評估指標和歷史規則匹配結果P得到當前各指標的權重b*。

4)風險值計算通過b*構建動態風險值計算公式，根據當前訪問請求的風險評估指標計算風險值R。

5)動態閾值計算采用歷史訪問請求的P和R實時計算風險閾值t。

6)最終控制決定根據系統需求綜合閾值t、規則匹配結果P和風險值R作出最終訪問控制決定。

3 自適應風險評估指標權重分配

3.1 問題分析

風險訪問控制模型中風險值量化方法可歸納為:

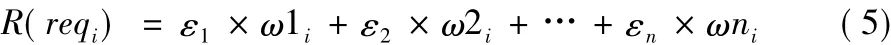
其中:ε1+ε2+… +εn=1;ωji(j=1，2，…，n)表示對第i條訪問請求reqi中第j個風險評估指標量化評估的值;εj(j=1，2，…，n)表示第j個風險評估指標的權重。當進行風險評估時，ωji取值由實際情況決定，所以εj為影響風險值的主要因素之一。大部分風險訪問控制模型采用的風險評估指標權重分配方法［6－8］為均分相等的權重，即 ε1= ε2= … = εn=1/n。但該方法存在以下3個不足:

1)風險評估指標權重固定;

2)風險值對訪問請求的靈敏度較低;

3)風險值的準確率較低。

針對上述3個不足，在風險值量化過程中，通過收集歷史訪問請求的風險評估指標和ABAC模塊的評估結果P，構造帶有自適應權重分配的風險值計算公式，并對新訪問請求的風險值進行預測。

3.2 自適應風險評估指標權重分配模型

根據歷史風險評估指標和P構建自適應權重分配模型，主要包括如下3個目標:

1)構造超平面將風險評估指標分為2類;

2)選擇合適的目標值;

3)風險評估指標權重滿足一定的約束條件。

針對上述3個目標，本文通過帶約束的多元線性回歸構造風險評估指標權重分配模型，并運用PR算法求解該模型。

本文使用風險評估指標(I，T，V)。其中:I表示當前訪問請求的訪問活動(讀、寫等)在歷史請求中被ABAC模塊允許(P=0)的頻率［7］;T根據訪問請求的主體屬性分配具體數值，角色屬性越高T越小，如:管理者的T值小于普通成員;V使用通用漏洞與披露(Common Vulnerabilities and Exposures，CVE)標準中關于Hadoop相關漏洞評分，即將本文模型部署在以Hadoop為基礎的云平臺下。

運用式(5) 和(I，T，V)，風險值為:

其中，ε1+ ε2+ ε3=1。若ε1、ε2、ε3由經驗設定且不能動態改變，則頻繁出現正常訪問請求的風險值R+大于惡意訪問請求的風險值R－，從而無法得到合理閾值，降低風險值的準確率。若 R+→0且R－→1，則R－－R+→1，由式(2)可知靈敏度S增加，閾值設定的區間范圍增大，風險值的準確率提高。而ABAC中正常訪問請求P=0，惡意訪問請求P=1，若R+/－→P，則可利用風險評估指標(用戶歷史行為信息和系統安全狀態)動態分配相應權重，所以本文設計的自適應風險評估指標權重分配模型為:

目標函數:

約束條件:

其中，ε為隨機誤差項。

3.3 PR 算法設計

本文利用廣度優先搜索和剪枝設計并優化PR算法以求解上述模型。由于PR算法利用矩陣的消去變換求解自適應風險評估指標權重分配模型，所以比使用二次規劃或線性規劃求解該問題更加簡單且計算量小［14］。優化后的PR算法在最小二乘法的基礎上首先分層存儲消去變換后的矩陣，然后逐層檢查并刪除不滿足條件的矩陣。PR算法設計如下。

算法1 PR算法。

輸入 用戶歷史風險數據X，規則評估結果Y;

輸出 風險評估指標權重b*，誤差極小值Qmin。

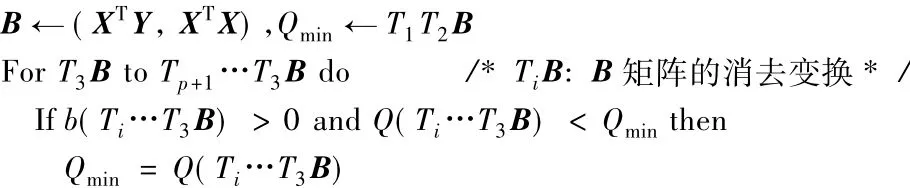
/*b():從消去變換后的矩陣中得到b*(矩陣最后

一列，第2行到倒數第2行的元素)，Q():從消去變換后的矩

陣中得到Qmin(矩陣最后一行，最后一列的元素)*/

End if

原料：肥雞1只、無核李子脯125克、蘋果3-4個、洋蔥和胡蘿卜各1個、生姜1小塊、面粉2大勺、精鹽和胡椒各適量

End for

4 實驗結果與分析

4.1 實驗環境與數據

為驗證本文提出的自適應權重分配方法，在PC上搭建實驗環境。1)硬件配置:Inter Core i3-2350M CPU@2.30 GHz，4.0 GB RAM。2)軟件環境:64 位 Windows 7 操作系統，Matlab R2016a。

數據集由不同的訪問請求組成，每條訪問請求信息包含主體、客體、訪問活動和訪問發生時間4個主屬性，每個主屬性下分層存儲子屬性，子屬性由相應的成員組成，例如:主體={管理者，員工，非員工，…}，管理者={管理者1，管理者 2，…}等。

每條訪問請求是在4個主屬性的相應子屬性下隨機選擇成員組成，模擬生成5組訪問請求S1、S2、S3、S4和S5。S1至S4分別存在150個成員，每個成員在S1至S4中分別有10、100、1000和10000條訪問請求，S1至S4中訪問請求發生的順序隨機。S5為隨機生成的50條訪問請求，由正常訪問請求(P=0)和惡意訪問請求(P=1)間隔組成。

用ABAC策略評估5組訪問請求得到評估結果P;通過對用戶歷史行為信息和當前系統安全狀態量化得到5組訪問請求的風險評估指標(I，T，V)。設定歷史窗口w=1000，即量化當前訪問請求的(I，T，V)時，使用的用戶歷史行為信息為該請求發生前w條歷史訪問請求信息。

訓練集Settrain為S1到S4的風險評估指標數據(I，T，V)和ABAC模塊評估結果Ptrain，即:

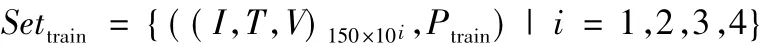
其中，(I，T，V)150×10i表示訓練集中第i組訪問請求存在150 ×10i條風險評估指標數據。

4.2 自適應權重分配評估實驗

實驗步驟設計如下:

步驟1 模擬生成5組訪問請求數據，構建訓練集Settrain和測試集Settest。

步驟2 通過S1至S4組訪問請求構建的訓練集分別訓練自適應風險評估指標權重分配模型，運用PR算法得到對應的 b*和 Qmin。

步驟3 將4組b*分別代入式(6)，構造自適應風險值計算公式。

步驟4 間隔1秒依次將測試集中的(I，T，V)代入自適應風險值計算公式，計算各訪問請求的風險值(如圖2中虛線所示)。

步驟5 為式(6)分配固定風險評估指標權重，構造固定風險值計算公式。固定指標權重采用文獻［6－8］中權重分配方法，即為各風險評估指標均分相等的權重(1/3，1/3，1/3)。

步驟6 間隔1秒依次將測試集中的(I，T，V)代入固定風險值計算公式，得到各訪問請求的風險值(如圖2中實線所示)。

步驟7 根據步驟4、步驟6中計算得到的風險值，使用式(1)、(2)和(3)得到相應的閾值t、靈敏度S和準確率Acc。

圖2中P=0或P=1的2條曲線分別采用2種指標權重分配方法計算測試集中正常或惡意訪問請求的風險值。從圖2可知，自適應風險評估指標權重分配使得風險值波動較大，即對于風險感知更靈敏;大部分P=0的訪問請求風險值被降低，大幅度減少R+≥t或R－≤t出現的頻率;P=1和P=0的訪問請求風險值分布間隔增加，使得閾值可設定的區間范圍增大，從而提高風險值的準確率。

從圖2(a)至圖2(d)可知，隨著訪問請求數量的增加，固定指標權重所得正常訪問請求的風險值和惡意訪問請求的風險值分布間隔減小，造成風險值對訪問請求的靈敏度下降;但自適應分配指標權重計算的風險值分布間隔逐漸增大，當訓練集的數量增加至十萬和百萬級時，正常訪問請求(P=0)的風險值中異常值(波峰)減少，所以本文提出的方法在大并發用戶數情況下適應性更強，更適合具有大量用戶且動態性強的云環境。

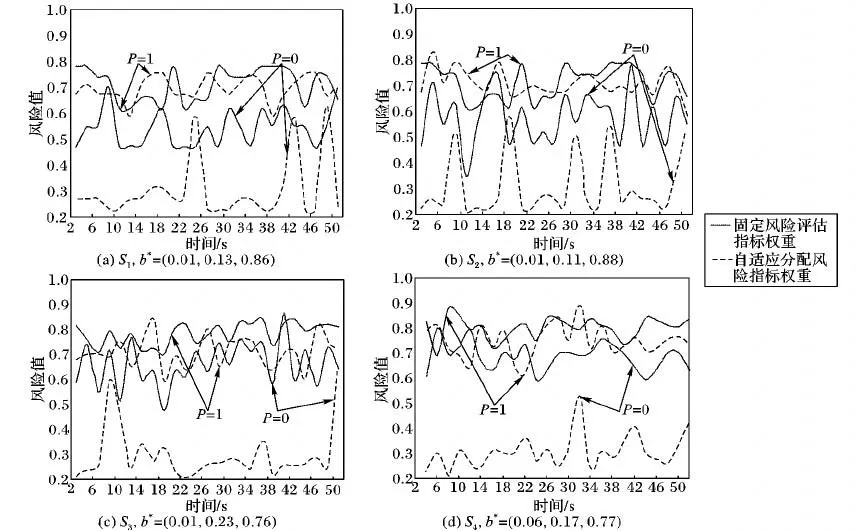
圖2 不同數量訪問請求的風險值分布Fig.2 Risk value distribution for different number of access requests

當選取不同數量訪問請求計算b*時，生成的風險評估指標權重不同，故在云平臺環境中，可通過用戶歷史行為信息和系統安全狀態實時動態地調整風險評估指標權重。

4.3 權重分配指標參數對比分析

為對比2種權重分配方法所得風險值的閾值、靈敏度和準確率，根據4.2節實驗步驟7，匯總并統計3種指標數據，如表1所示。

從表1可見，針對閾值t，本文方法所得風險值的閾值低于固定指標權重，由于R+被降低，R－被升高，使得R+與R－的差距增加，從而減小閾值，但閾值設定的區間范圍增大，使得閾值的設定更加靈活、合理。自適應分配指標權重所得風險值的閾值，基本穩定在0.5左右，而固定指標權重的閾值波動較大，運用式(1)可知，P=0或P=1訪問請求風險值整體出現升高或下降時，會導致閾值出現波動，所以本文方法在大規模用戶訪問時，能夠維持P=0和P=1訪問請求風險值整體的穩定性。

針對靈敏度S，本文方法所得風險值的靈敏度高于固定指標權重。運用式(2)可知，P=0和P=1的訪問請求風險值的分布間隔越大，靈敏度越高。自適應分配指標權重所得風險值的靈敏度基本維持在0.4以上，隨著訪問請求數量的增加，靈敏度不斷升高。而固定指標權重所得風險值的靈敏度隨著訪問請求數量的增加，逐漸降低。所以本文方法所得風險值不僅靈敏度較高，而且分布具有穩定性。

針對準確率Acc，本文方法所得風險值的準確率高于固定指標權重。隨著訪問請求數量的增加，自適應分配指標權重所得風險值的準確率整體呈現上升的穩定趨勢，而固定指標權重風險值的準確率較低，且不穩定，有一定程度的波動。所以本文方法更適用高并發、高動態的云環境。

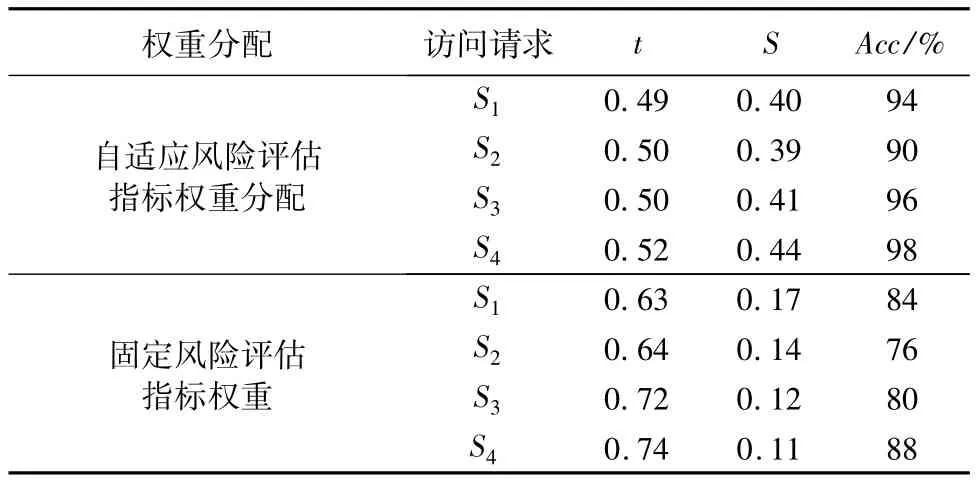
表1 2種權重分配方法相關參數Tab.1 Related parameters of two weight allocation methods

4.4 準確率和靈敏度實驗

通過靈敏度和準確率2種指標，對比分析本文方法構建的風險訪問控制模型與其他風險訪問控制模型的性能。本節實驗通過Matlab仿真實現本文模型、文獻［8］提出的DRAC模型和文獻［9］提出的基于系統安全風險的訪問控制模型。由于3種風險訪問控制模型均是通過規則評估和風險評估等模塊構建，所以分別實現這些模塊，并根據數據的流向連接不同的模塊。設計實驗步驟如下:

步驟1 通過Matlab仿真實現本文模型、DRAC模型和基于系統安全風險的訪問控制模型。

步驟2 將4組訪問請求S1、S2、S3和S4分別代入步驟1中3種模型進行訓練。

步驟3 將S5代入經過S1至S4訓練完成的3種模型，記錄S5中訪問請求的風險值。

步驟4 通過式(2)計算風險值對訪問請求的靈敏度S，匯總并統計得到S的分布情況(如圖3(a)所示)。通過式(3)計算風險值的準確率Acc，匯總并統計得到Acc的分布情況(如圖3(b)所示)。

從圖3(a)可見，本文模型所得風險值的靈敏度整體維持在0.4以上。基于系統安全風險的訪問控制模型在數據量較小時(S2)，風險值的靈敏度達到0.43，但隨著數據量增加，靈敏度下降至0.32。DRAC模型所得風險值的靈敏度隨著數據量的增加，也在逐漸增加，最高達到0.39。所以本文模型所得風險值的靈敏度整體優于另外2種模型。

從圖3(b)可見，在訪問請求數量為S1時，本文模型所得風險值的準確率為94%，略高于另外2種模型。但在S2時，基于系統安全風險的訪問控制模型風險值的準確率達到最高95%，而本文模型出現波動，準確率下降至90%。隨著數據量的不斷增加，本文模型風險值準確率最高達到98%，明顯優于另外2種模型。

DRAC模型根據數據流方法量化風險評估指標，但數據流方法對歷史窗口w依賴較大，若w的選擇不合理，則風險評估指標效果減弱，所以隨著數據量的增加，該模型風險值的準確率和靈敏度都要低于本文提出的模型。基于系統安全風險的訪問控制模型根據模糊層次分析法分配風險評估指標權重，但分配后的權重若更改需進行復雜的代數運算，所以在數據量較小時，該模型的靈敏度和準確率要優于DRAC模型，但隨著數據量的增加，權重無法動態自適應調整的劣勢凸顯，準確率和靈敏度都低于DRAC模型和本文提出的模型。

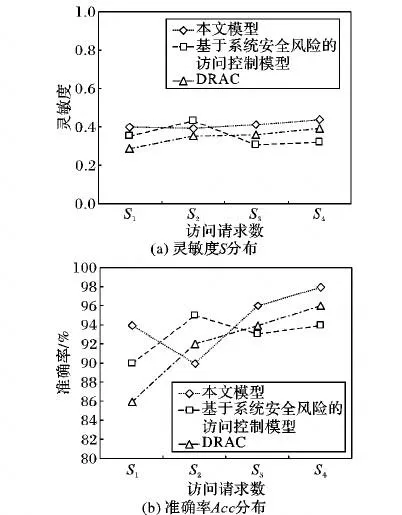
圖3 準確率與靈敏度分布Fig.3 Distribution of accuracy and sensitivity

4.5 響應時間對比分析

根據文獻［8，15］，訪問控制模型對訪問請求的響應時間是模型可擴展性的重要度量標志，反映訪問控制模型在用戶不斷增加時的處理能力。本文實驗對比4.3節3種模型和文獻［15］提出的基于動態屬性的風險感知訪問控制(Dynamic Attribute-based Risk Aware Access Control，DA-RAAC)模型，分析4種風險訪問控制模型對不同數量訪問請求的響應時間，具體步驟如下:

步驟1 使用Matlab仿真實現DA-RAAC模型。該模型基于屬性基加密(Attribute-Based Encryption，ABE)模型和風險引擎，為方便起見，僅實現風險引擎模塊。

步驟2 隨機生成640、1 280、…、20 480條訪問請求，分別使用4種模型對6組訪問請求進行訪問授權。

步驟3 記錄并統計4種模型對6組訪問請求的響應時間，結果如圖4所示。

從圖4可知，本文提出的模型比另外3種模型響應時間更短。由于數據流和模糊層次分析等數學方法，需要長時間的代數運算，DA-RAAC模型中存在大量的布爾運算，所以本文方法構建的模型在保證準確率和靈敏度都較高的情況下，響應時間也明顯低于其他3種模型。綜上，本文提出的帶有自適應指標權重分配的風險訪問控制模型更適用于有較大用戶量的云環境。

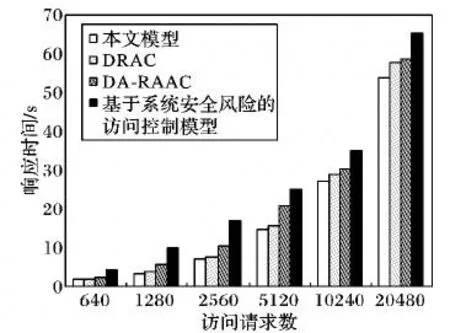
圖4 不同模型響應時間Fig.4 Response time of different models

5 結語

本文針對大多數風險訪問控制模型風險評估指標權重固定的不足，提出云平臺訪問控制自適應風險評估指標權重分配方法。該方法提出風險評估指標權重分配模型，并改進配方回歸算法高效求解相應權重，構建動態風險值計算公式。該方法解決風險評估指標權重主觀性和靜態性問題。實驗表明該方法所得風險值具有較高的準確率和靈敏度，且有更短的響應時間。

在本文所提風險訪問控制模型中，規則匹配模塊僅使用ABAC策略，但對于高并發的云環境，ABAC策略更加復雜且動態性弱。未來的研究重點是通過改進規則匹配模塊，進一步增強風險訪問控制模型的動態性。