高階非線性Schr?dinger方程的精確行波解
高正暉
(衡陽師范學院數學與統計學院,湖南 衡陽 421002)
本文將研究一類高階非線性Schr?dinger方程:
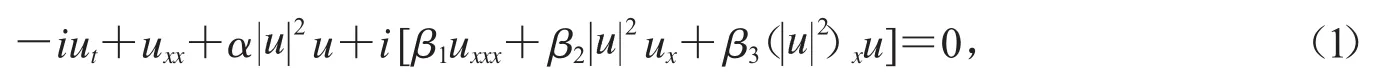
其中 α,β1,β2,β3分別是方程的實系數,i2=-1,u 是關于 x,t的復值函數,是u的復共軛.非線性Schr?dinger方程是數學物理中的一類重要的非線性演化方程,它在量子力學、非線性光學、電磁學、等離子體理論、固體物理學以及玻色-愛因斯坦凝聚等眾多領域有著廣泛的應用.從傳統的觀點來看,求非線性偏微分方程的精確解是十分困難的,然而,近幾十年來,對某些非線性偏微分方程的精確求解獲得了許多有效的方法,如直接積分法,混合指數法,齊次平衡法,雙曲函數展開法及Baclund變換法等[1].Peng Yan-ze等[2]用修正的映射方法和推廣的映射方法,得到了方程(1)的一些精確行波解,但這些方法不能揭示其行波解如何依賴于方程中的參數變化,其行波解具有什么樣的動力學性質也不清楚.近幾年來,郭柏靈,劉正榮[3]、李繼彬[4-8]、劉正榮[9]等運用動力系統的分支理論對一些非線性發展方程的精確行波解進行了研究,建立了求非線性發展方程精確行波解的新方法.本文將應用動力系統的分支理論,對方程(1)的行波解的平面相圖做細致的分析,根據這些分析,給出方程(1)的精確行波解的參數表示.
1 方程(1)的行波變換
考慮方程(1)如下形式的行波解
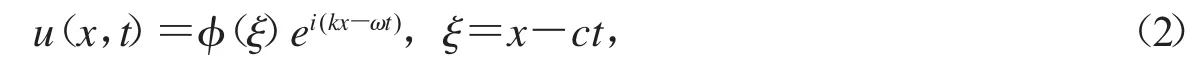
其中φ(ξ)表示振幅,k為波數,ω為圓頻率,c為行波的波速.
將式(2)代入方程(1),則有
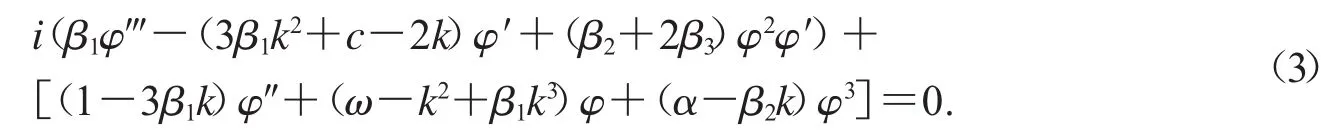
由方程(3)可得
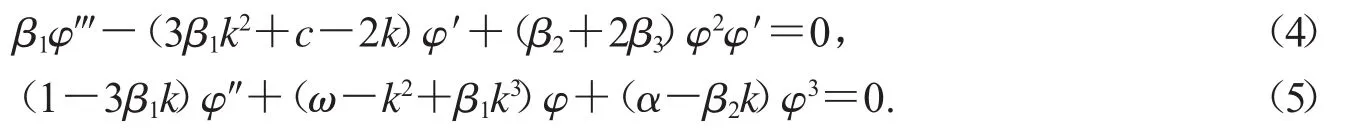
對方程(4)積分一次并取積分常數為0,可得
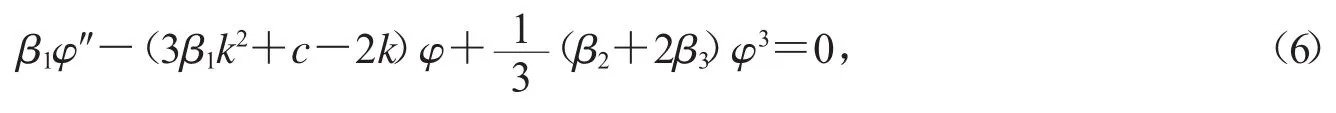
比較方程(5)、(6),可得
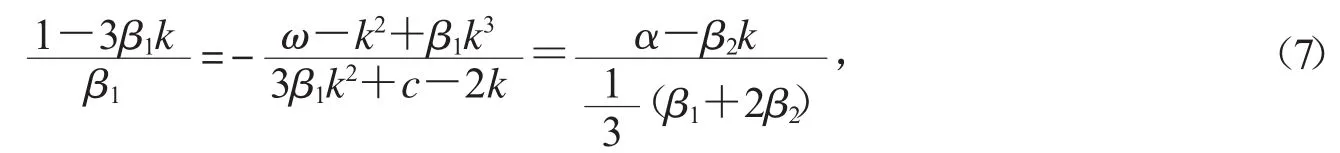
由(7)解得
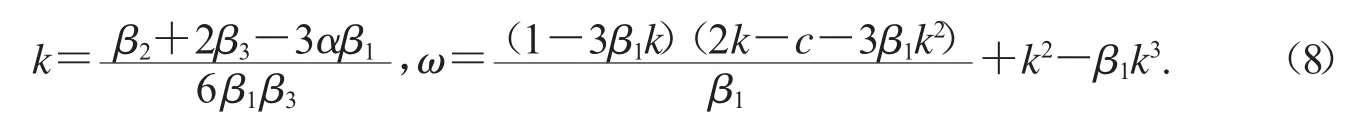

令φ′=y,則可得以下平面自治系統

2 系統(9)的平面相圖
顯然,系統(9)是一個Hamilton系統,它有首次積分
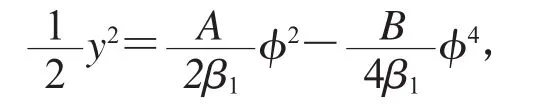
因此,系統(9)的Hamilton函數為
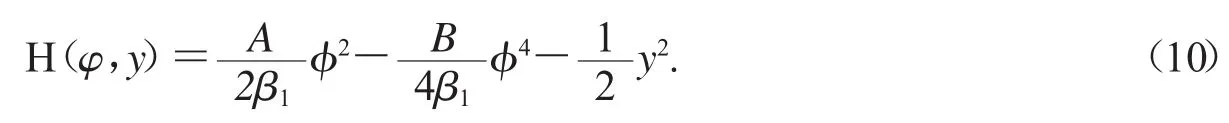
對于系統(9),其平衡點滿足方程組
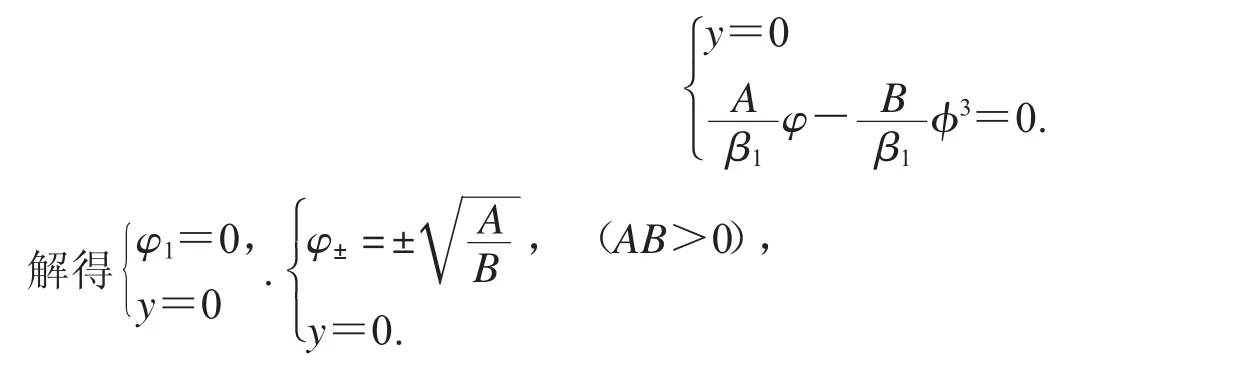
因此,當AB>0時,系統(9)有平衡點O(0,0)及平衡點,0).記M(φi,yj)為系統(9)的線性系統在平衡點(φi,yj)的系數矩陣,其Jacobi行列式因此,該系統在平衡點O(0,0)的Jacobi行列式為在平衡點的Jacobi行列式為根據平面動力系統理論,對于平面可積系統(9)的平衡點,若J>0,則它是中心;若J<0,則它是鞍點;若J=0并且在平衡點的Poicare指標為0,則它是尖點,否則,該平衡點是高次平衡點.
記 h0=H(0,0)=0,
情形1:當AB<0時,系統(9)有唯一的平衡點O(0,0).
1)當 β1A>0 時,因此,平衡點 O(0,0)是鞍點.
2)當 β1A<0 時,因此,平衡點 O(0,0)是中心.
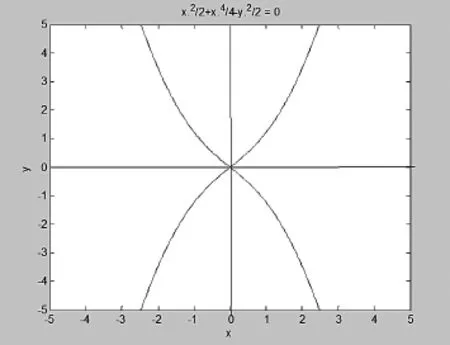
圖1 β1A>0的平面相圖
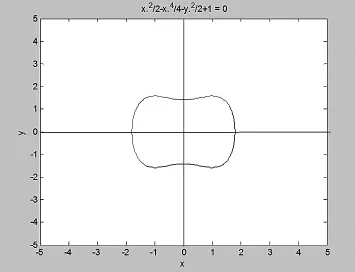
圖2 β1A<0的平面相圖
情形2:當AB>0時,系統(9)有平衡點O(0,0)及平衡點
3)當 β1A>0 時,因此,平衡點O(0,0)是鞍點,平衡點是中心.
4)當 β1A<0 時,因此,平衡點是 O(0,0)中心,平衡點是鞍點.
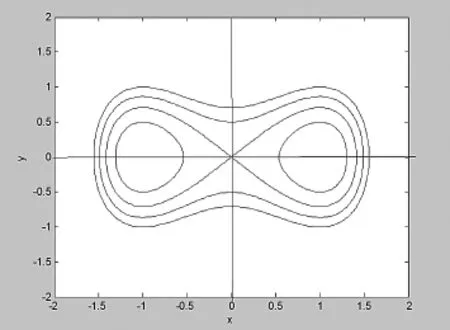
圖3 β1A>0的平面相圖
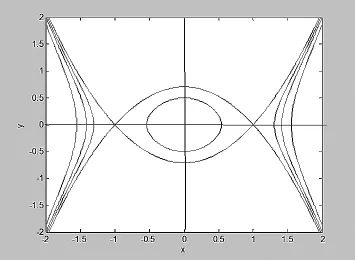
圖4 β1A<0的平面相圖
3 方程(1)的精確行波解的參數表示
根據上述系統(9)的平面相圖,可得
情形 1:當 AB<0時,系統(9)有唯一的平衡點 O(0,0).
1)當 β1A>0 時,因此,平衡點 O(0,0)是鞍點.
取 h=h0=0,由代入系統(9)的第一個方程得

此為第四種橢圓方程,因此有解

因此,方程(1)有精確行波解
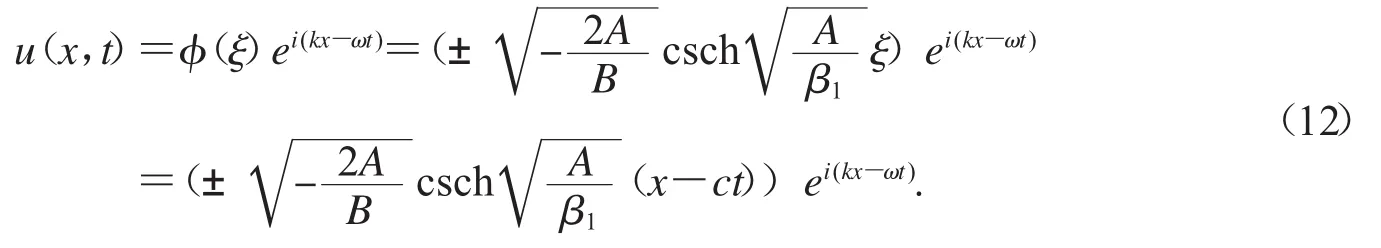
2)當 β1A<0 時,因此,平衡點 O(0,0)是中心.
取h∈(-∞,0),對應于由H(φ,y)=h所定義的曲線是系統(9)的周期軌,因此,系統(9)有周期解.由可得
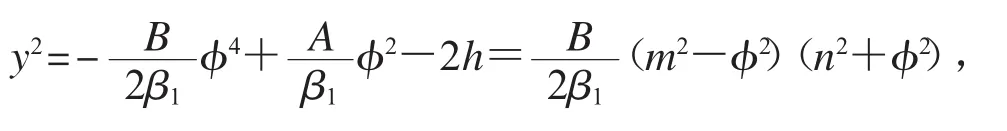
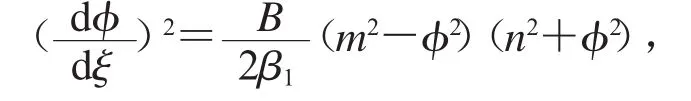
此為第一種橢圓方程,因此有精確周期波解
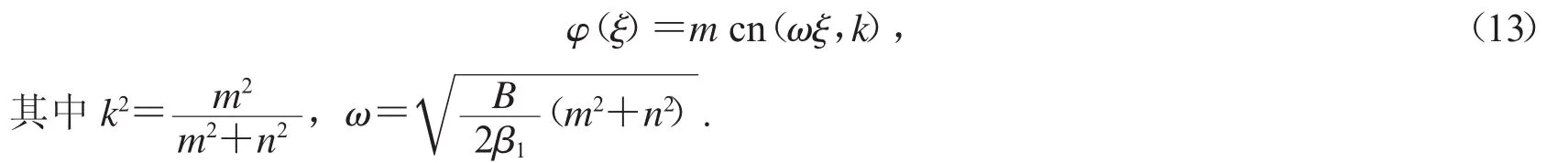
因此,方程(1)有精確行波解
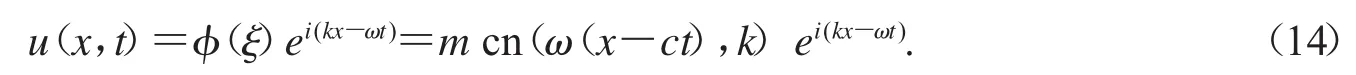
情形2:當AB>0時,系統(9)有平衡點O(0,0)及平衡點
3)當 β1A>0 時,因此,平衡點O(0,0)是鞍點,平衡點是中心,且系統(9)有過鞍點的同宿軌Γ1,其內部包含中心.
取 h=h0=0,由可得代入系統(9)的第一個方程得
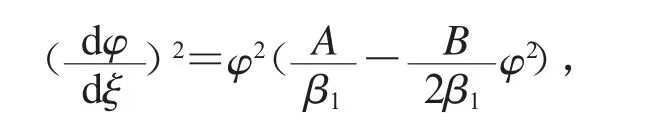
此為第四種橢圓方程,因此有解
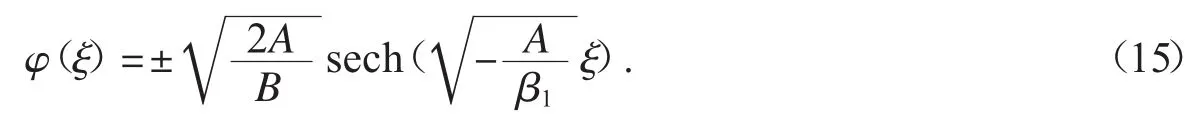
因此,方程(1)有精確行波解
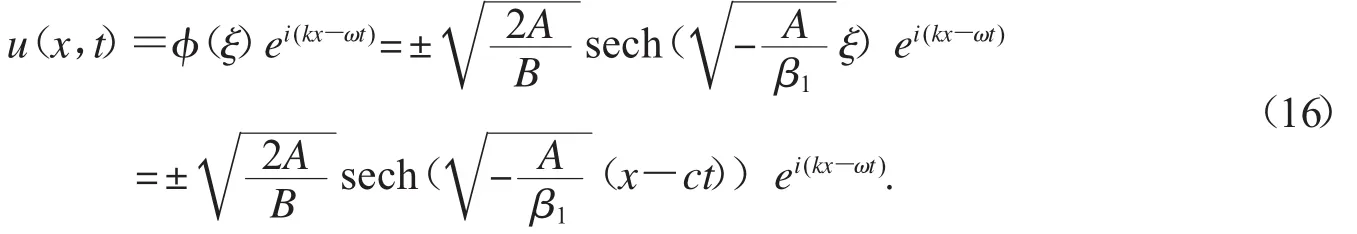
4)當 β1A<0 時,因此,平衡點O(0,0)是中心,平衡點是鞍點,且系統(9)有過鞍點的異宿軌Γ2.
取由可得代入系統(9)的第一個方程得
因此有解
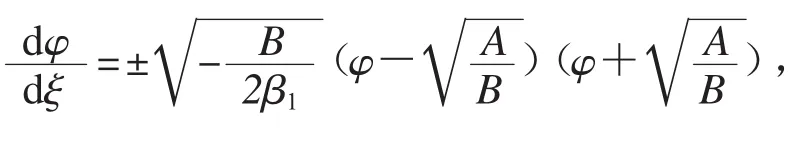
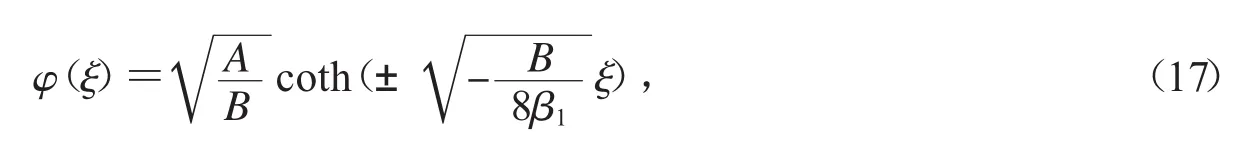
所以,方程(1)有精確孤波解
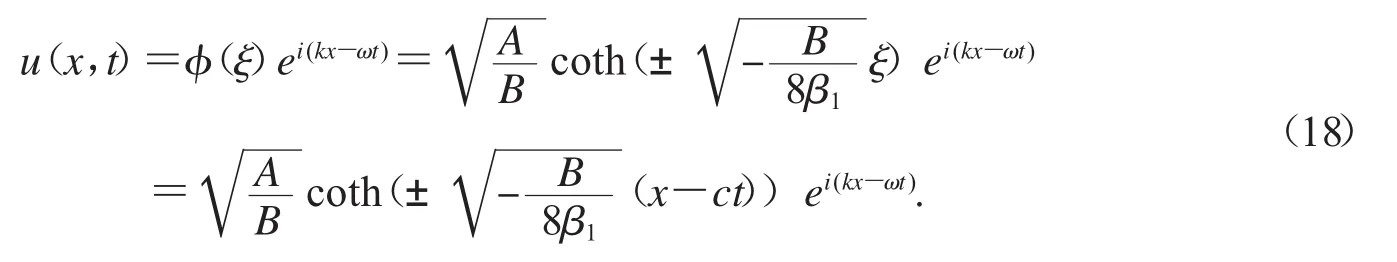
4 結語
本文應用平面動力系統分支理論的方法,對一類高階非線性Schr?dinger方程進行了研究,在參數平面上給出了該方程的精確行波解的分支相圖,從而揭示了其行波解與參數的依賴關系,并獲得了該方程的精確行波解的參數表示.

