基于壓汞法的煤基質壓縮對孔隙分形特征的影響
金 毅 趙夢余 劉順喜 劉仙鶴
(1. 河南理工大學資源環境學院,河南省焦作市,454003; 2.中原經濟區煤層(頁巖)氣協同創新中心,河南省焦作市,454003)
煤層氣資源的勘探開發是全球油氣產能增長的重點研究領域,其中對儲層孔隙結構特征的研究是實現煤層氣高效開采的關鍵。煤儲層孔隙結構極其復雜,表現為多尺度、非均質性和各向異性特征,其復雜程度直接影響煤層氣在儲層中的賦存和運移,因此孔隙結構的精細化、定量化表征成為儲層物性評價的研究熱點和難點。
基于分形幾何理論,國內外眾多學者通過不同的試驗測試技術,發現煤儲層的孔隙結構具有良好的分形特征,可用分形維數來定量表征孔隙結構的非均質性、孔隙表面的粗糙程度及破裂程度等。一些學者利用壓汞實驗,推導了煤儲層孔隙結構分形維數的計算方法,并依據分形曲線的形態和分形維數的大小判斷孔喉連通性、分選性和孔隙分布情況,進而分析儲層非均質性的強弱和儲集性能的高低。通過對比分形維數與煤的變質程度、水分、灰分和孔隙度的關系,部分學者認為分形維數在一定程度上反映了儲層演化過程中物性變化的差異程度。然而,由于煤基質具有壓縮性,導致煤樣在高壓下進汞量高于真實孔容,影響了煤孔隙結構分形維數計算的準確性。同時,對于前人研究的孔隙分形維數計算方法,其統計特征不利于尺度不變本質內涵的理解與挖掘,進而影響煤儲層孔隙結構的分形定量描述。
因此,本文基于分形拓撲理論推導了孔隙結構分形維數的計算方法,結合壓汞和液氮吸附試驗數據,探討了煤基質壓縮效應對孔隙結構分形特征的影響,并與前人的孔隙結構分形維數計算方法進行了對比分析,揭示了煤儲層孔隙結構分形定量描述的本質特征。
1 分形理論與分形維數計算方法
在當前實際應用的各孔隙結構分形維數計算方法中, 典型且被廣泛接受的方法有體積-壓力分形模型和體積-孔徑分形模型,本文基于分形拓撲理論建立了數目-尺度分形模型。
1.1 分形拓撲理論
通過總結以往分形理論在儲層孔裂隙中的應用研究,提出了分形拓撲理論,認為分形對象的分形維數是由蘊含其中的分形行為決定的,并且這種分形行為與分形構建體的幾何屬性無關,表現為不同尺度的分形構建體在空間上的拓撲關系。這種分形拓撲關系由兩個尺度不變參數—尺度縮放比P和尺度覆蓋率F確定,其定義見式(1):
(1)
式中:P——尺度縮放比;
li——代表分形對象的尺度;
F——尺度覆蓋率比;
N(li)——代表每一級尺度li對應的分形對象的數目,個。
基于分形拓撲的定義,得分形維數的尺度不變定義見式(2):
(2)
對于統計自相似的單分形對象,其在任意方向上的尺度縮放比P是相等的。由于分形對象的隨機分布特征,同一尺度下各分形對象的尺度覆蓋率F不盡相同,但由統計意義上的尺度不變性可得尺度覆蓋率的期望〈F〉為一常數。若每一級分形對象的分形拓撲定義為Ω(P,Fj),各尺度下尺度覆蓋率的期望〈F〉見式(3):
(3)
式中:Ne——每一尺度下分形對象的分形拓撲的種類數目,個;
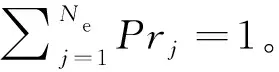
1.2 煤儲層孔隙結構的分形描述
1.2.1 體積-壓力分形模型描述
基于固體質量分形模型(Menger海綿體或Sierpinski地毯),并結合毛細血管壓力與孔徑之間的關系,儲層孔隙結構分形維數的計算式見式(4):
(4)
式中: dV——孔容增量, mL/g;
dPc——壓力增量,MPa;
Pc——進汞壓力,MPa。
記dV/dPc與Pc雙對數曲線斜率為K,可以得出煤孔隙結構的分形維數為D=4+K。
1.2.2 體積-孔徑分形模型
根據分形理論中統計自相似對象的分形維測定原理,賀承祖和華明琪推導出當rmin?rmax時,孔半徑小于r的累積孔隙體積分數S的表示式見式(5):
(5)
記潤濕相飽和度S與孔隙半徑r的雙對數曲線的斜率K,可得分形維數D=3-K。
1.2.3 數量-尺度分形模型
根據1.1所述分形拓撲理論,煤巖孔隙結構的分形行為主要是由不同孔徑的孔隙之間的分形拓撲決定的。假設煤是由大小不同的固體顆粒填充堆積而成的多孔介質,在一個體積為VT的煤體中,孔隙的最大孔徑為λmax,其對應孔隙數目為N(λmax)。由分形拓撲的構建原理可知,當分形行為相同時,孔隙的大小與孔隙數目之間的尺度不變性滿足式(6):
(6)
結合上式可得不同孔隙半徑ri對應的孔隙體積V(ri)見式(7):
V(ri)=αN(ri)rid=C0〈F〉irid
(7)
式中:C0=αN(rmax),α為幾何形狀因子,球形取4π/3,立方體取1;
d——歐幾里得空間維。
綜合式 (2) 、式 (6) 和式 (7) ,不同尺度下孔隙體積V(r)與孔隙半徑r的比例關系見式(8):
V(r)∝rd-D
(8)
進而得分形多孔介質中孔隙分布數量-尺度關系見式(9):
N(r)∝r-D
(9)
根據壓汞實驗中的增加進汞體積V(r),可計算半徑為r的孔隙數目N(r),記N(r)和r的雙對數曲線的斜率為K,得分形維數D=-K。
總體來說,上述方法都是以經典的數量-尺度模型為基礎,結合不同的目標屬性,只是依據的多孔介質模型或推導方式有所不同。這些方法的共同之處在于它們大多以累積孔體積作為分形維數的變化參數,但由分形體的構成與分形行為的演化可知,分形維數對孔隙結構的差異變化主要反映在各孔徑段的增加孔體積變化。
2 樣品及實驗分析
2.1 樣品及實驗
本文7個煤樣分別采自山西沁水煤田陽泉礦區(樣品YQ1和YQ2)、晉城礦區(樣品JC1和JC2)和貴州織納煤田(樣品GZ1T、GZ2和到Q2)的井下新鮮采集面。所有煤樣進行真密度的測定,經研磨后的直徑統一篩分至40~60目,一式兩份,于烘箱中干燥12 h后分別進行壓汞和液氮吸附實驗。壓汞實驗采用AutoPore IV 9500型全自動壓汞儀,壓力范圍689.5 Pa~413.7 MPa,孔徑測量范圍3 nm~360 μm,實驗中汞接觸角為130°,汞表面張力設為4.85×10-3N/cm,實驗過程執行標準GB/T 21650.1-2008;液氮吸附實驗采用ASAP 2020比表面積與孔隙度測試儀,BJH法計算孔隙體積。
2.2 基質壓縮系數與體積校正
在壓汞實驗中,隨著壓力的增大,煤基質體積受到不同程度的壓縮,如果忽略進汞過程中汞和儀器本身的壓縮性,煤基質壓縮系數kc見式(10):
(10)
式中:kc——煤基質壓縮系數;
Vc——煤基質體積,mL/g;
dVc/dPc——相應壓力增量下煤基質的體積變化。
對于可壓縮的煤巖多孔介質,其視進汞量的變化主要受到煤基質壓縮效應和孔隙填充效應的影響,見式(11):
ΔVobs=ΔV+ΔVc
(11)
式中:ΔVobs——視進汞量,mL/g;
ΔV——孔體積增量,mL/g;
ΔVc——煤基質體積壓縮量,mL/g。
結合液氮吸附測試范圍,選擇合適的校正區間為10.99~206.74 MPa(對應孔徑區間6~100 nm),且研究表明煤樣校正前對應校正區間內的進汞量與壓力成線性關系,可將ΔVobs/ΔPc視為常數C,得ΔVc/ΔPc見式(12):
(12)
式中:ΔPc——壓力增量, MPa;
ΔV——6~100 nm范圍內的孔隙體積 (可由氮氣吸附數據獲得),mL/g。
由于實驗中ΔVc/ΔPc近似視為常數,可用ΔVc/ΔPc代替dVc/dPc,結合式(10)、式(12)可得煤基質的壓縮系數kc。通過統計分析各樣品在基質壓縮校正前后的孔體積變化,發現各煤樣對應的孔徑分布曲線形態相似,考慮到圖幅有限,從中選取煤樣GZ1、GZ2、GZ3和YQ1的壓汞數據,得到其校正前后累計進汞量的對比如圖1所示。
由圖1可以看出,當壓力小于10 MPa時,校正前后孔體積無明顯差異,此時煤基質壓縮效應可忽略不計。當壓力大于10 MPa時,校正前后的孔體積出現了明顯偏差,這表明高壓階段煤基質壓縮效應對孔隙結構影響顯著。當壓力超過120 MPa時,校正后的孔體積不再增大,甚至出現逐漸減小的趨勢,表明在極高壓力下煤內部孔隙結構已發生十分復雜的變化,不再滿足上述校正的前提條件。綜上,本文采用孔徑范圍為10~100000 nm的測試數據進行煤孔隙分形特征的研究。煤樣壓縮系數及孔隙參數見表1。

圖1 煤樣可壓縮性校正前后累計進汞量的對比

樣品編號kc/10-10m2·N-1 壓汞法6~100 nm孔體積b/mL·g-16~100 nm孔體積a/mL·g-1N2吸附6~100 nm孔體積/mL·g-1誤差率/%ρHe/g·cm-3GZ11.310.0165470.0006010.00046634.21.59GZ21.360.0155990.0004230.00035842.41.59GZ31.430.0184470.0009470.00062628.01.54YQ11.250.0170.0008920.00065624.61.5YQ21.140.0173240.0007560.00050432.91.312JC10.80.01040.0004650.00027636.01.536JC20.780.01150.001870.0016395.91.42
注:kc為煤基質壓縮系數;b為未校正數據;a為校正數據
由表1可以看出,煤樣的壓縮系數為0.78×10-10m2/N到1.36×10-10m2/N,與前人所測結果0.35×10-10m2/N到3.13×10-10m2/N之間相符。當孔徑范圍在6~100 nm時,以液氮吸附試驗得到的孔體積作為標準體積,由壓汞實驗測得的孔體積在校正前后的變化量相對于標準體積的偏差值在5.9%~42.4%之間,且校正后的煤樣總孔容更接近標準體積,說明未進行壓縮校正的進汞量無法反映真實的孔隙分布情況。
3 校正前后煤樣的分形特征分析
利用煤樣壓汞數據,本文采用體積-壓力分形模型、體積-孔徑分形模型以及數量-尺度分形模型對比分析了校正前后煤孔隙結構分形特征的差異,分別以方法1、方法2和方法3進行表述。
通過分析校正前后3種方法的分形曲線形態差異,發現校正前分形曲線大多呈分段結構,校正后分形曲線多具有良好的線性特征。而方法3的雙對數曲線在校正前后的總體趨勢沒有發生很大變化,均表現為一段式線性相關特征。通過對比各方法對應分形曲線的形態,發現同種方法得到的分形曲線趨勢基本相同,因此為了表現3種方法對應分形曲線的差異,從7個煤樣中選取GZ1和GZ3作為典型煤樣進行了對比分析,各煤樣擬合得到的分形維數統計結果如表2所示。
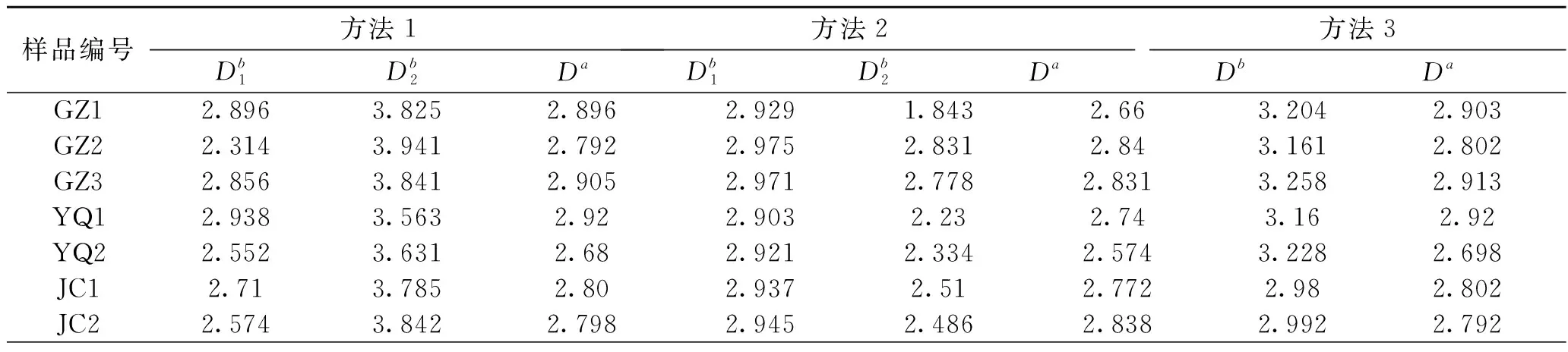
表2 校正前后煤樣分形維數
注:b為未校正數據;a為校正數據
方法1校正前的分形曲線明顯呈兩段式,典型煤樣的dV/dPc~Pc的雙對數圖如圖2所示,前半段(大孔、中孔)分形曲線的線性擬合相關性高,分形維數D1b<3,說明此區間的孔隙結構具有分形特征,而后半段(微孔、小孔)的線性擬合相關性較差,分形維數D2b>3,此區間孔隙結構不再具備分形特征。校正后分形曲線為一段式,分形維數Da<3,孔隙結構在整個孔徑范圍內具有良好的分形特征。
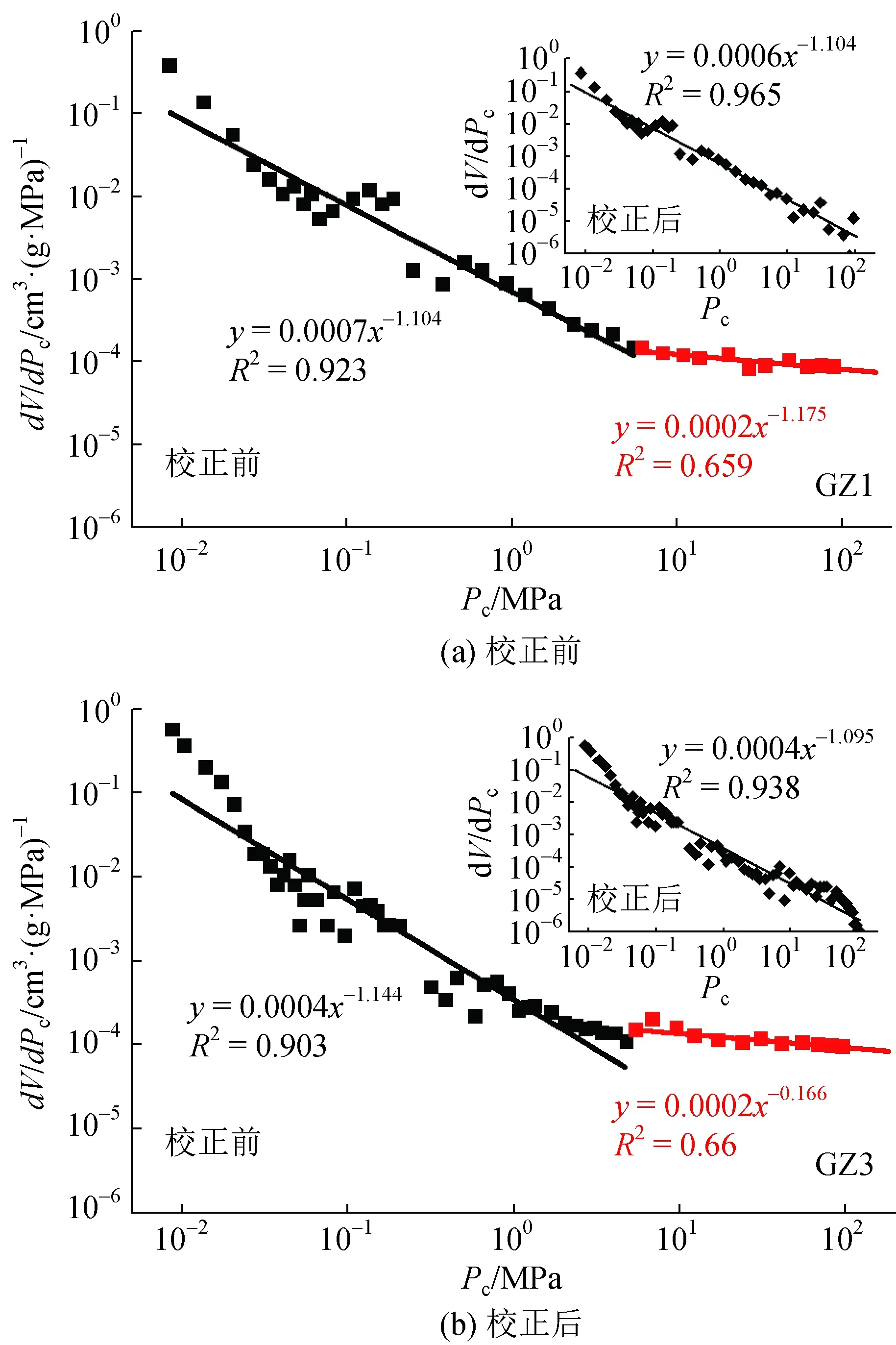
圖2 方法1典型煤樣的dV/dPc~Pc的雙對數圖
方法2校正前分形曲線GZ1分為兩段,GZ3分為三段,校正后分別變為一段和兩段,典型煤樣校正前后S~r的雙對數圖如圖3所示。在大中孔區間,分形維數D1b的值較高,在2.90~2.98之間,在微小孔階段,分形維D1b的值較小,甚至小于2,這與方法1得到的分形維數的變化情況相反,說明兩種方法的計算原理存在很大差異。
對比上述兩種方法的分形曲線,發現其轉折端的孔徑在60~100 nm,但兩者的曲線形態存在明顯差異。因為方法1利用的是各級孔徑對應的孔體積與進汞壓力的關系,計算的是當前壓力下各級孔隙的分形維數;方法2利用累積孔體積與孔半徑的關系,得到的是當前壓力下被汞侵入的所有孔隙的分形維數。
此外,方法1校正后的分形曲線基本表現為一段連續性較好的線性段;方法2校正后分形曲線的連續性雖有一定增強,但仍具有分段特征。主要是因為校正后孔體積的減小導致各孔徑段孔體積的差異被縮小,使得整個孔徑范圍內的孔體積分布連續性增強。典型煤樣校正前后N(r)~r的雙對數圖如圖4所示。
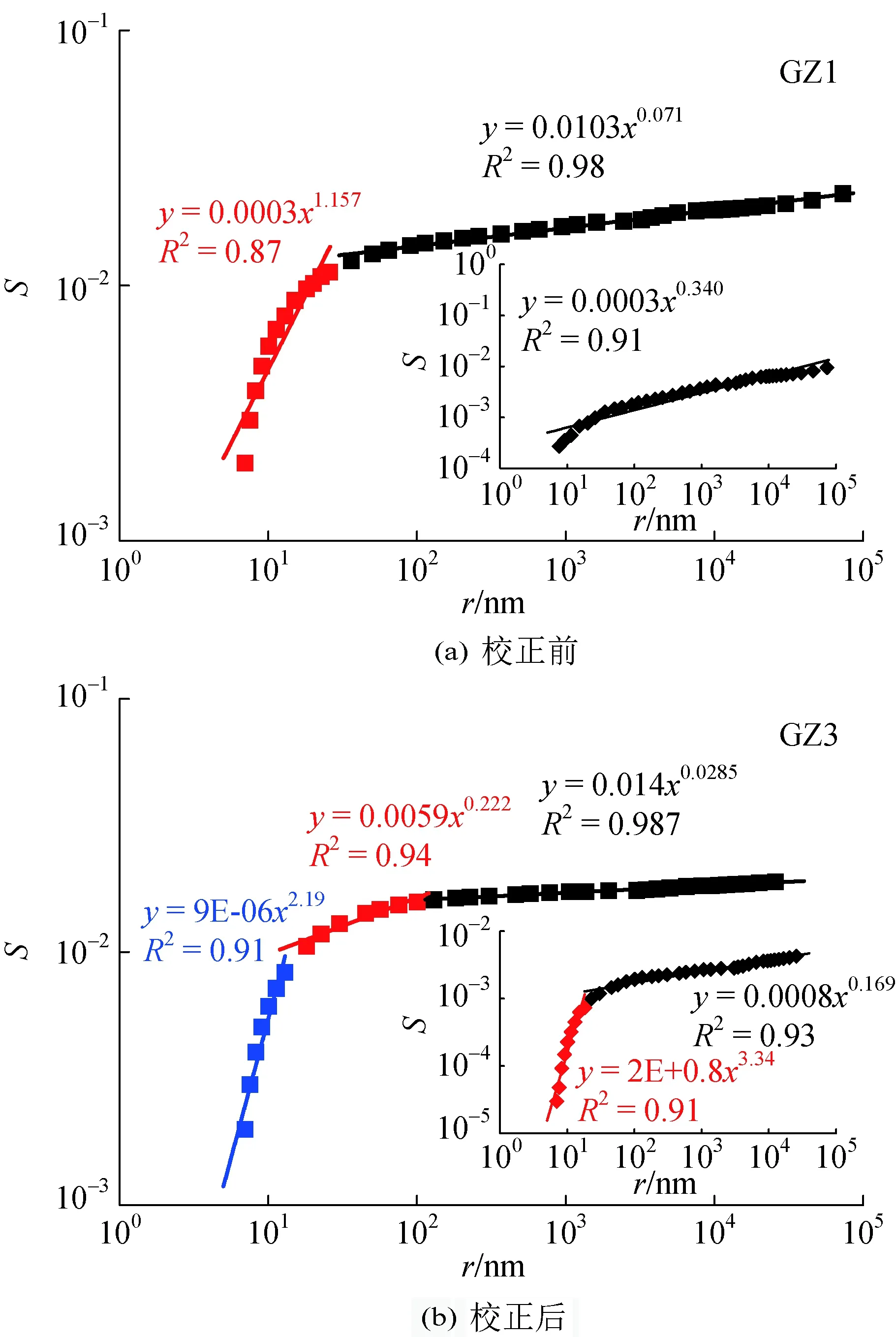
圖3 方法2典型煤樣校正前后S~r的雙對數圖
對比表2數據中針對3種方法計算的分形維數,發現同一樣品在校正前后的孔隙分形維數大小差別明顯,且校正后各方法得到的分形維數也存在一定差異。 方法1與方法3校正后的分形曲線形態十分相近,計算得到的分形維數偏差在0.01左右,表明利用分形拓撲理論推導的孔隙分形維計算方法來定量表征煤儲層孔隙結構特征是可行的;方法2校正后分形維數與其他兩種方法的偏差較大,在0.03~0.24之間,并且其分形曲線還存在分段的情況,因此使用該方法描述孔隙分形特征時可能存在較大誤差。
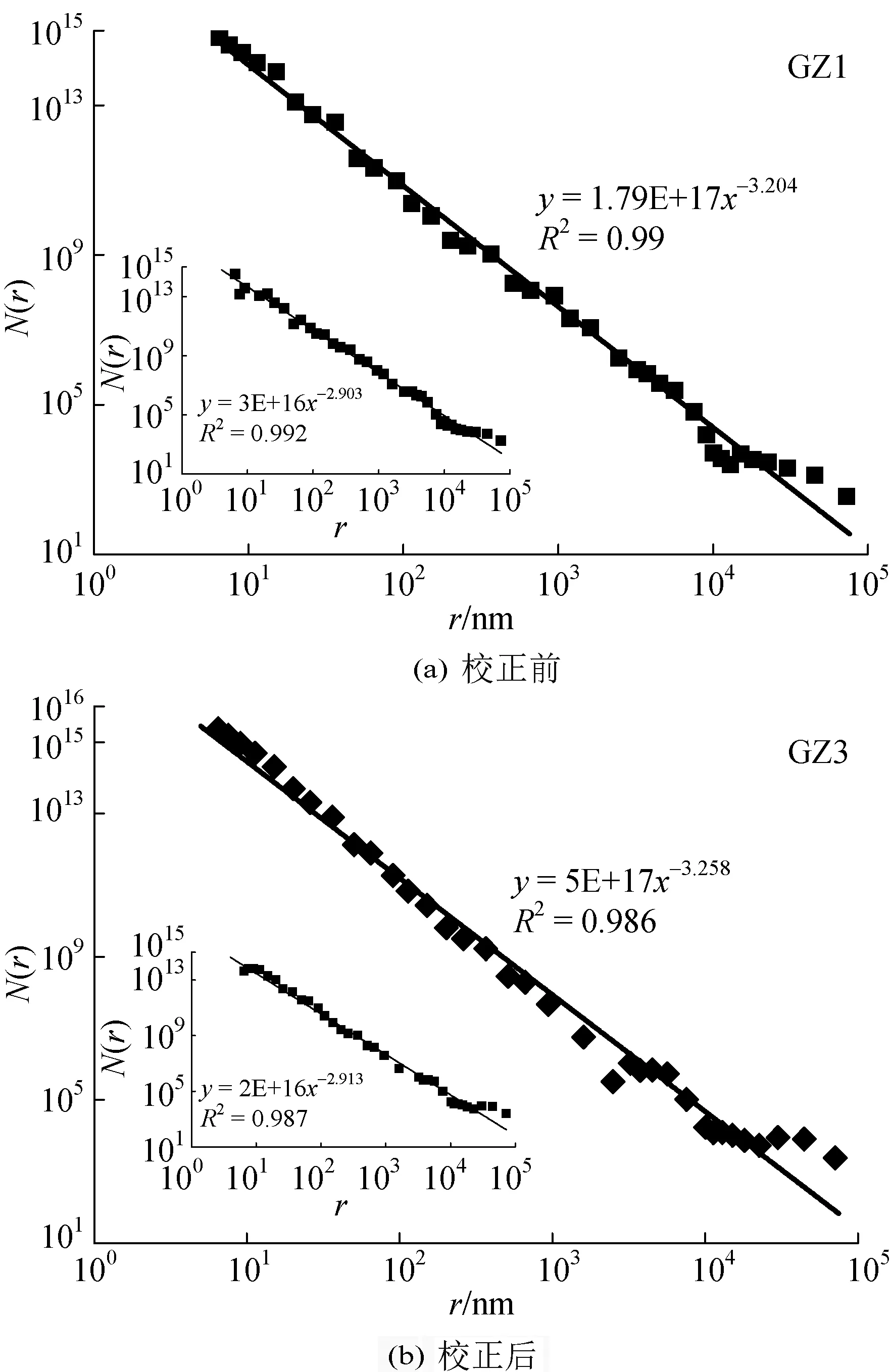
圖4 方法3典型煤樣校正前后N(r)~r的雙對數圖
盡管3種方法所得分形維數有所差別,但經校正后分形維數都要比校正前要小。校正前由于未考慮煤基質壓縮效應,孔隙空間占整個煤樣的比例變大,引起孔隙體積偏高,孔隙結構復雜化,導致分形曲線呈現分段式,部分孔徑區間內分形曲線不存在分形特征。以樣品GZ1為例,方法3得到的分形維數在校正前為3.20,超過了真實范圍2~3,校正后減小為2.90。因此,經校正數據得到的分形維數更符合實際情況,適用于描述煤孔隙結構的分形特征。
4 結論
(1) 根據分形拓撲理論推導的孔隙分形維數計算方法與傳統的分形維計算模型結果相近,能夠定量表征煤儲層孔隙結構的復雜程度。
(2) 樣品煤基質壓縮系數在0.78×10-10m2/N~1.36×10-10m2/N之間,當壓力大于10 MPa時,煤基質壓縮效應明顯,必須考慮,當壓力大于120 MPa時,煤體內部孔隙結構發生復雜變化,不適宜進行壓縮系數校正。
(3) 不同分形維數計算方法對應的分形曲線特征存在較大差異,校正前3種方法分別呈現出一段式和多段式,校正后分形曲線的形態大都呈現單段式,表明校正前由于煤基質壓縮引起的孔隙體積增加會增大孔隙結構的復雜程度,從而增強孔隙結構的非均質性,導致部分孔徑區間內不存在分形特征或分形特征減弱。
(4) 校正前分形維數普遍偏大,甚至超過了3,而校正后分形維數減小,在2~3之間,孔隙結構在整個孔徑范圍內都具有良好的分形特征,說明校正后的分形維數能夠更加準確地描述真實的孔隙結構特征,表征孔隙結構的復雜性。

