支持向量回歸機建立排氣溫度模型研究

夏存江

1 引言

航空發動機是飛機的核心動力系統，而且是一種結構復雜高度精密的機械，對之實施有效的狀態監控是保障飛機安全性，可靠性和經濟性的重要途徑。發動機排氣溫度（exhaustgastemperature，EGT）是最能反映發動機運行情況的性能參數，通過分析EGT測量值偏離對應基線值的偏差值，可監控和預測發動機的健康狀態及其性能衰退趨勢。EGT的基線值是生產廠家通過大量的試驗綜合統計獲得，屬于航空發動機狀態監控核心技術，廠家并未公布，國內航空公司的狀態監控也只是停留在監控軟件的簡單操作[1]。

為了避免過度依賴發動機生產廠家，目前在航空發動機基線挖掘方面，一些研究學者對其進行了較深入的研究。如文獻[2]應用正交實驗設計原理和最小二乘曲線擬合的方法建立了JT9D三種類型的發動機基線方程；文獻[3]采用基于核函數的多元非線性回歸分析方法，對Rolls-Royce公司的Trent700發動機基線方程進行挖掘，建立了標準化過程中的核函數和性能參數的偏差值模型，文獻[4]中，以CFM56-5B航空發動機為例，利用RBF神經網絡建立了EGT的基線模型。在以往的工作中，采用不同方法對航空發動機的基線進行挖掘，但很少采用支持向量回歸機（SVR）對民航發動機EGT基線方程進行建模分析，并且之前的研究結果和模型精度并不是很理想。

以民航某主力型號發動機為例，采用支持向量回歸機的方法建立了精度較高且對未知數據預測能力較強的EGT基線模型。

2 樣本數據預處理

航空發動機常年在高溫、高壓等惡劣環境下工作，其相關參數的測量較為困難，常見的問題主要有數據測量誤差大、傳感器易發生故障、某些數據甚至難以采集等[5]。收集到的航空發動機相關性能參數的數據若不加以預處理，則很難準確反映航空發動機的實際健康狀態。因此，首先從不同地區的兩家航空公司收集某型號發動機的2014年5月至2015年5月的實際飛行數據，然后對其進行預處理以用于后續的發動機基線模型訓練和驗證。預處理的內容主要包括對原始數據中的異常點判別與粗大誤差剔除。

異常點的識別方法是用以往數據信息來判斷當前點是否異常，即：對于某一時間序列｛Xi｝ni=1，判別t=i個數據是否異常，可根據t=i之前的序列｛Xi｝nn=1進行判斷。判別方法可以是根據子序列｛X預測 t=i時的值為 Yi，預測精度為 δi，如果 Yi?［Yi-δi，Yi+δi］，則稱Yi為異常點。針對航空發動機數據特點，采用拉依達準則（3σ準則）來判別異常點，它以數據足夠多為前提，其預測值取為前面數據的算術平均值，預測精度為3σ（3倍的標準差）[6]。流程圖，如圖1所示。

圖1 拉依達法則流程圖Fig.1 Float Chat of Pauta Criterion

根據圖1所示的異常點的判別方法，將收集到的數據剔除粗大誤差之后得到回歸模型的輸入樣本訓練數據500組和驗證數據300組。

目前，有很多文獻資料中對于模型的輸出樣本即發動機基線值的求解方法進行了研究，計算方法如式（1）：

式中：EGTb—EGT對應的基線值；EGTk—將EGT的測量值EGTm轉化為標準大氣條件下的修正值。

查閱原始文獻[7]，該型號發動機參數基線值的實際求解方法如下：

由式（2）可知發動機EGTb的計算公式如（3）式：

由于EGT基線模型是基于大氣條件等因素建立的，所以公式（3）中采用EGT的直接測量值EGTm計算EGTb，國內許多研究學者采用的式（1）是不符合廠家系統的規律。為了提高后續訓練的EGT基線模型的推廣泛化能力，考慮選取一架飛機的兩臺發動機的相關數據，由于其在巡航狀態下工作在同一個外界環境，獲得的發動機的性能參數值也趨近于相同，并且對應同樣的基線，所以利用式（3）分別計算兩臺發動機的EGTb并且取兩者平均值，得到EGT基線模型的輸出樣本空間EGTb，從而保證了模型的普遍適用性。

3 支持向量回歸機建模原理

支持向量機（support vector machines，SVM）是數據挖掘問題的一種新的、有效的方法，理論基礎是統計學理論，在小樣本建模領域表現出優異的推廣泛化能力。處理回歸問題的向量機稱為支持向量回歸機（support vector regression，SVR），是結構風險最小化的實現，它通過非線性函數，將輸入樣本轉換到高維線性特征空間，巧妙地解決了維數問題，并且能夠有效避免神經網絡出現的過學習和局部最小化的缺陷，最終得到一個全局最優解[8]。

假設n個訓練數據樣本（xi，yi），式中：xi—第i個輸入樣本；yi—對應的輸出值。首先考慮用線性函數進行回歸，方程為：

在數值計算中，對于xi的預測值f（xi），允許其與真實值yi存在一定的誤差ε，需要引入合適的損失函數，SVR常選擇的是不敏感損失函數[9]：

基于結構風險最小化原則，就得到了線性的支持向量回歸算法，回歸估計問題轉換為解決一個在約束條件下的最優化問題，形式為：

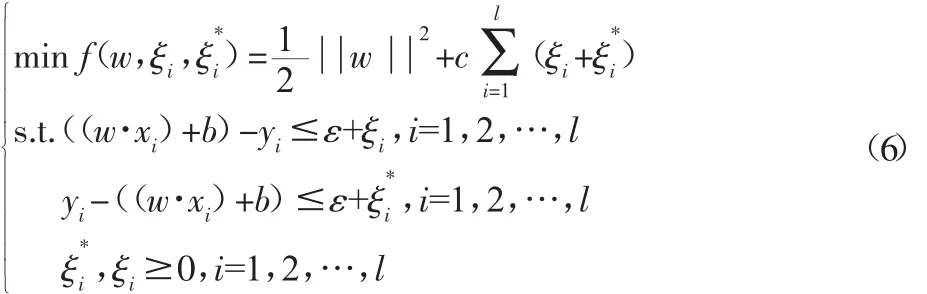
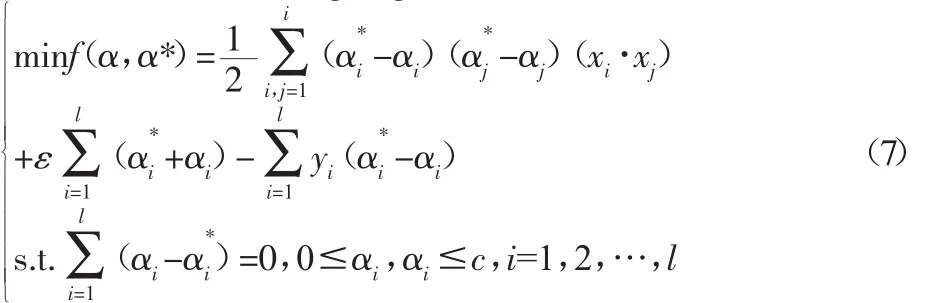
通過求解可得到αi和α*i，并根據Kuhn-Tucker定理計算得到b，最終得到線性回歸函數。

對于非線性回歸，支持向量回歸機的基本思想是利用合適的內積函數把訓練數據轉換到某一個高維Hilbert空間中，然后在此高維空間中用函數進行線性回歸，最終取得在原空間非線性回歸的效果。此內積函數稱為核函數K（xi，xj）。

4 發動機EGT基線建模

分析原廠家系統氣路參數基線值的求解過程可知，發動機EGT基線模型是一個關于有關測量參數的多元非線性模型，所以可以將其的求解描述為如下的數學模型：

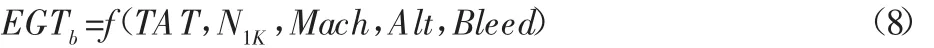
式中：TAT—外界大氣總溫；N1K—風扇修正轉速；Mach—飛機飛行馬赫數；Alt—飛機飛行高度；Bleed—飛機環境控制及飛機和發動機防冰系統的引氣量。

由于收集的數據中ECS數據都為1，飛機巡航狀態客艙引氣處于打開狀態，對基線影響很小，故bleed不予考慮；通過確定每個自變量與EGTb相關程度來驗證數據的準確性，求解的每個變量與EGTb的復相關系數，表明：N1K和TAT與EGTb高度相關，Alt和Mach與EGTb中度相關，與廠家理論模型吻合。因此在選擇EGT基線模型的訓練集時，分別構造以下的輸入變量和輸出變量：

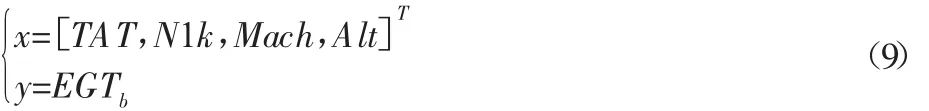
在模型訓練的過程中，核函數的選擇是決定高維特征的的關鍵因素，由于高斯徑向基核函數能夠實現較好的非線性映射，且具有較寬的收斂域，擬合和預測精度高，是較為理想的回歸依據函數，將選用該核函數，具體表達式如下[10]：

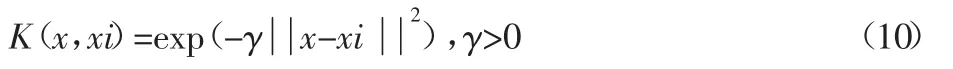
SVR模型的性能取決于選擇適當的參數，懲罰因子c，高斯徑向基核函數中的g和ε-不敏感損失函數中的精度p都是影響回歸的重要因素，為了解決經驗法選取支持向量回歸機參數效率低，取值不準確的問題，采取遺傳算法（Genetic Algorithm，GA）對參數進行尋優，尋優結果，如圖2所示。

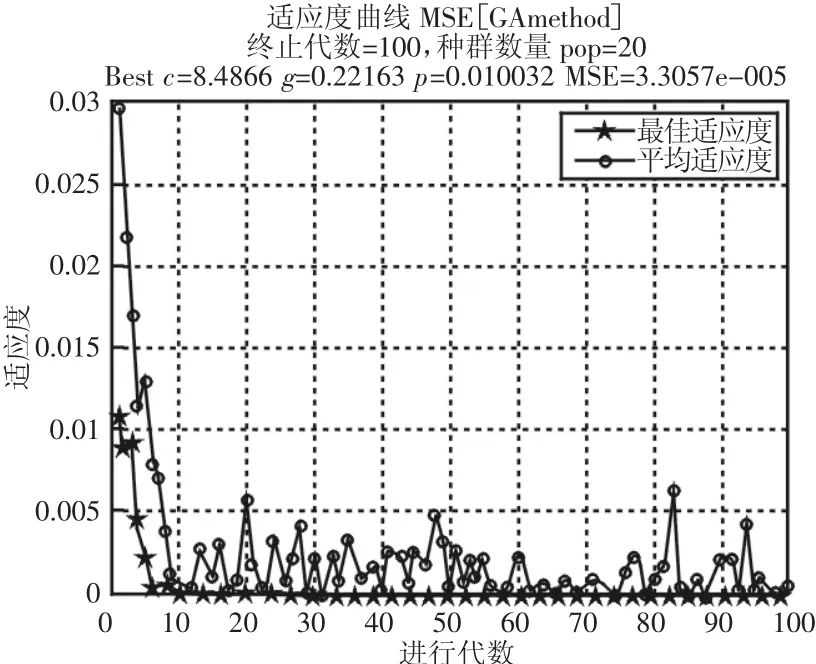
圖2遺傳算法尋找最佳參數的適應度曲線Fig.2 Fitness Curve of the Best Parameter by Genetic Algorithm

圖2 中適應度是在遺傳算法中描述個體性能的主要指標，用于評價個體的優劣程度。從圖中可以得到懲罰因子c，核函數中的g和精度 p 的優化值，分別為 c=80.4866，g=0.22163，p=0.010032，此時的均方誤差為3.3057e-5，滿足其精度要求。

結合之前構造的輸入變量和輸出變量，利用選擇的核函數和用遺傳算法尋優得到的最佳參數進行發動機EGT基線模型訓練，對訓練數據進行預測得到相應的EGTb預測值，表1列舉了10組數據訓練結果的誤差對比，平均相對誤差只有-0.0164%，表明支持向量回歸機下的模型在EGT基線求解中具有較高的精度。SVR評價回歸模型精度的高低，采用平均平方相關系數（mean squared error，MSE）和平均相關系數（squared correlation coefficient，R2）作為評價指標。此模型的參數指標為：

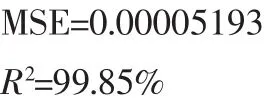
由模型參數指標和表1所示的結果可知：EGT基線預測值與原始值高度相關，模型具有很好的回歸性能。

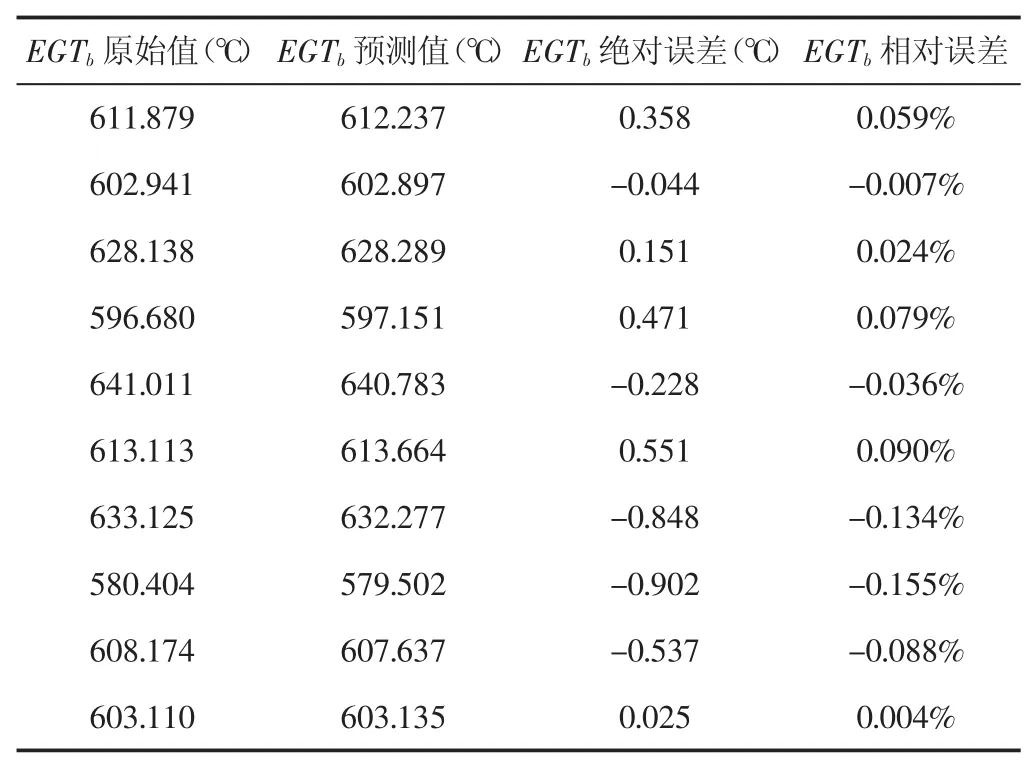
表1 訓練樣本的EGTb的預測值與原始值對比Tab.1 Comparison Between Predicted Values and Original Values of EGTb for Training Sample

5 EGT基線模型的驗證

為了進一步驗證訓練的EGT基線模型的精確性和推廣泛化能力，即對未知樣本的預測能力，選取另外一臺相同型號的發動機的300組數據作為測試樣本。隨機選取該測試樣本預測值與真實值對比的50組數據，對比結果，如圖3所示。

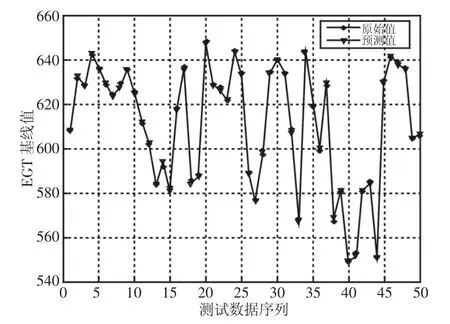
圖3 測試樣本的EGTb預測值與原始值對比Fig.3 Comparison Between Predicted Values and Original Values of EGTb for Test Sample

從圖3的對比圖可以看出，測試樣本的EGT基線預測值與真實值很接近，絕對誤差在0線上均勻分布且無突變情況，驗證了本次模型具有較強的泛化能力，同時說明了求解方法符合SVR的結構風險最小化的原則。

航空發動機氣路偏差值的大小以及變化趨勢能夠反映發動機氣路部件性能衰退的程度和速度，許多航空公司以氣路參數偏差值作為發動機性能健康狀態評估的主要參數。所以采用本次挖掘的EGT基線模型和式（1）計算EGT的偏差值，得到EGT偏差值的對比結果，如圖4所示。

從圖4可以看出，通過該模型求出的EGT偏差值與原始值基本吻合，準確度較高，在發動機的性能監控中具有實際意義。

圖4 EGT偏差值的預測值與原始值對比Fig.4 Comparison Between Predicted Values and Original Values of Deviation Value for EGT

6 結束語

以民航某主力型號發動機為例，收集其相關性能參數數據，將拉依達法則作為數據預處理方法，建立模型的輸入和輸出訓練樣本，采用遺傳算法進行相關參數的優化計算，提高了模型求解精度和效率，選用另一臺相同型號的發動機的性能參數數據作為測試樣本，并且求解測試樣本的EGTb預測值的偏差值，誤差結果表明：利用支持向量回歸機建立的EGT基線模型具有較高的精度且對未知數據的預測準確性高，使用該模型計算的EGT的偏差值與廠家返回的數據很接近，在航空發動機性能監控過程中具有非常高的實際應用價值。